Zagadnienia

13.1 Motywacje
13.2 Definicje
13.3 Równowaga Nasha
13.4 Twierdzenia o istnieniu

13. Gry iterowane

13.1. Motywacje

Używa się też nazwy gry powtarzane (repeated games, infinitely repeated games, iterated games).

W świecie realnym podmioty interakcji, gracze często wchodzą w interakcje z tymi samymi przeciwnikami, partnerami. Perspektywa przyszłych interakcji z tym samym graczem może istotnie wpływać na wybór strategii graczy.

Gry powtarzane opisują np. sytuacje wielokrotnych interakcji społecznych, altruizmu, kary etc. Gracz musi uwzględnić wpływ granej akcji na przyszłe akcje przeciwników. Pojedyńcza interakcja jest opisywana pewną grą strategiczną (stage game, one–shot game). Gracze wielokrotnie powtarzają tę grę, podejmując za każdym razem decyzję o wyborze akcji jednocześnie (ogólniej–nie znając decyzji pozostałych graczy), natomiast znając poprzednie akcje pozostałych graczy.

Jest wiele przykładów powtarzalnych interakcji z których każda jest np. opisywana tą samą jednokrotną grą strategiczną i które nie mają określonego terminu zakończenia, horyzontu czasowego. Z drugiej strony w wielu przypadkach termin zakończenia takich interakcji nie odgrywa istotnej roli w planowaniu strategii graczy. W takich przypadkach model z nieskończona liczbą interakcji może być lepszy do opisu strategii graczy.

Gry iterowane dzielimy na skończone i nieskończone. Gra skończona to ciąg skończenie $n$ razy powtarzanej gry jednokrotnej, przy czym $n$ jest znaną liczbą.

Przykład 13.1

n-krotny Dylemat Więźnia.

Metoda indukcji wstecznej zastosowana do równoważnej EGwII pokazuje że racjonalny gracz gra defekcję w każdej grze pojedynczej.

Gra nieskończona (będziemy uzywać skrótu GN lub GI: Gra Iterowana) to nieskończony ciag takich gier. Będziemy zajmowali się powtarzanymi grami nieskończonymi. Motywacją do ich wprowadzenia jest np. fakt że w wielu sytuacjach nie znamy liczby przyszłych interakcji.

Ponieważ nie można zastosować metody indukcji wstecznej, więc w nieskończonym Dylemacie Więźnia nie jest oczywiste jakie akcje powinien podejmować racjonalny gracz–świadomość kary w przyszłych grach za defekcję w pewnej chwili (czyli obniżenia wypłaty) może spowodować wybór kooperacji.

Wypłaty będziemy opisywać jako sumę wypłat z gier pojedynczych. Aby uniknąć wypłat nieskończonych wprowadzimy czynnik dyskontujący wypłaty. Formalnie będzie to odpowiadało sytuacji gdy po każdej grze pojedynczej jest niezerowe prawdopodobieństwo $w$ że bedzie grana nastepna gra pojedyncza. Wartość oczekiwana liczby takich gier jest wtedy równa $1/(1-w)$ .

Przykład 13.2

Iterowany Dylemat Więźnia (IDW) (Iterated Prisoner's Dilemma, IPD)

Jest to najbardziej–ze względu na zastosowania–popularny przykład gry nieskończenie powtarzanej. Gdy nie jest explicite powiedziane inaczej, wyjściową grą pojedyńczą jest dwuosobowy Dylemat Więźnia $[R,S,T,P],\ T>R>P>S$ . Aby utrzymywanie kooperacji było bardziej opłacalne niż naprzemienne zdradzanie i kooperowanie, zakłada się dodatkowo że $2R>T+S$ .

13.2. Definicje

Niech GS= $<N,(A_{i}),(u_{i})>$ będzie grą strategiczną, rozgrywaną w dyskretnych chwilach czasu $t=1,2,...$ (stage game). Zakładamy że w chwili $t$ gracze znają akcje przeciwników podejmowane w $t-1,...$ . Założenie to będzie w szczególności potrzebne do zdefiniowania strategii graczy. Oznaczmy

$a^{t}\in\times _{{i\in N}}A_{i}$

–profil akcji granych w chwili $t$ .

Definicja 13.1

Historia do (chwili) $t$ (in time t) jest to ciąg profili akcji

$h^{t}=(a^{0},a^{1},...,a^{{t-1}}),\ \ t=1,2,...,$

gdzie $a^{0}$ oznacza profil pusty, formalnie potrzebny do określenia akcji granej początku gry.

Na przykład dla dwóch graczy historia do $t$ jest to ciąg $t-1$ par akcji.

Używając nomenklatury z teorii GE mówimy że historia jest zakończona wtedy i tylko wtedy gdy jest nieskończona. Formalnie historia zakończona to nieskończony ciag profili $(a^{0},a^{1},a^{2},...)$ .

W celu zdefiniowania strategii w GN oznaczmy:

$H^{t}$ –zbiór wszystkich historii do $t$ . Możemy napisać

$H^{t}=\times _{{s=1}}^{{t-1}}A.$

Definicja (ważna) 13.3

Strategia (czysta) gracza $i$ jest to nieskończony ciąg funkcji

$s_{i}:=(s^{1}_{i},...,s^{t}_{i},...),$

gdzie $s^{t}_{i}:H^{t}\rightarrow A_{i}$ –funkcja zwracająca akcję gracza $i$ po historii do $t$ ; $s_{i}^{t}(h^{t})$ jest to akcja gracza $i$ po historii $h^{t}$ (czyli w chwili $t$ ) gdy stosuje strategię $s_{i}$ .

Przykład 13.4

Strategia grim–trigger (strategia cynglowa) w Iterowanym DW (IDW):

$s_{i}^{1}(a^{0})=C$ ,

$\displaystyle s_{i}^{t}(a^{0},a^{1},...,a^{{t-1}})=\left\{\begin{array}[]{ll}C,&gdy\ a_{{-i}}^{\tau}=C\ dla\ \tau=1,2,...,t-1\\ D,&wpp.,\end{array}\right.$

(13.1)

Gracz stosujący tę strategię zaczyna akcją C i gra C do chwili gdy przeciwnik zagra D, i od tego momentu gra D niezależnie od akcji przeciwnika.

Przykłady innych strategii w IDW.

All C–zawsze kooperuj.
All D–zawsze zdradzaj.
TFT–Wet Za Wet (Tit For Tat): w pierwszej rundzie koperuj, następnie powtarzaj ostatni ruch przeciwnika.
TFT2–Wet Za 2 Wety (Tit For 2 Tats): zdradzaj gdy przeciwnik zdradził w 2 poprzednich rundach, wpp. kooperuj.
BRUTAL: w pierwszym ruchu kooperuj. Następnie: jeżeli przeciwnik kooperuje, zdradzaj co drugą rundę, jeśli w pewnej rundzie zdradzi, graj cały czas D.
WIN–STAY, LOSE–SHIFT (PAVLOV): Graj C w pierwszej rundzie, po (C,C) i po (D,D) wpp. graj D.
STAND1: w pierwszym ruchu zdradź. Jeżeli przeciwnik też zdradził, to zdradzaj we wszystkich kolejnych rundach, jeśli kooperował to kooperuj we wszystkich kolejnych rundach, w obu przypadkach niezależnie od akcji przeciwnika.
STAND2: w pierwszych 2 ruchach zdradź. Jeżeli w nich przeciwnik chociaż raz zdradził, to zdradzaj we wszystkich kolejnych rundach, jeśli nie, to kooperuj we wszystkich kolejnych rundach, w obu przypadkach niezależnie od akcji przeciwnika.

Uwaga 13.1

Analogicznie jak dla GE, profil strategii wszystkich graczy $(s_{1},...,s_{n})$ wyznacza historię zakończoną. Na przykład dla $n=2$ jeżeli obaj gracze grają grim-trigger, historią zakończoną będzie nieskończony ciąg par (C,C) (poprzedzony $a^{0}$ ).

Definicja 13.4

Wypłata gracza $i$ z nieskończonego ciągu profili akcji $h=(a^{1},a^{2},...)$ jest dana wzorem

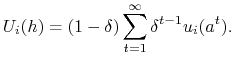$U_{i}(h)=(1-\delta)\sum _{{t=1}}^{\infty}\delta^{{t-1}}u_{i}(a^{t}).$

Normalizacja $1-\delta$ pozwala obliczać wypłaty gry pojedynczej i powtarzalnej w tych samych jednostkach. Na przykład jeżeli wypłaty mają postać $u_{i}(a^{t})=2$ , to $U_{i}(h)=2$ .

13.3. Równowaga Nasha

Zdefiniujemy równowagę Nasha.

Ponieważ profil strategii $s=(s_{1},...s_{n})$ generuje nieskończony ciąg akcji $h$ , więc użyjemy symbolu $U_{i}(s)$ na oznaczenie wypłaty gracza $i$ z profilu strategii $s$ . Formalnie:

$\tilde{U}_{i}(s):=U_{i}(h),$

gdzie $h$ jest zakończoną historią generowaną przez profil strategii $s$ . Na przykład dla dwoch graczy stosujących strategię grimm–trigger w DW [2,0,3,1], $\tilde{U}_{i}(s)=2.$

Definicja (ważna) 13.5

Profil $s$ jest RN w GI jeżeli

$\tilde{U}_{i}(s_{i},s_{{-i}})\ge\tilde{U}_{i}(s^{{\prime}}_{i},s_{{-i}})\ \ \forall i=1,...,n.$

Przykład 13.5

W IDW profil w którym strategia każdego gracza to: graj D po każdej historii do $t$ jest RN.

Okazuje się że nie jest to jedyna RN w IDW.

Przykład 13.6

Profil $s:=(GT,GT)$ ( $GT$ =grim–trigger) jest RN.

Pokażemy to dla 2-osobowego IDW z macierzą wypłat gry pojedynczej $[2,0,3,1]$ . Wypłata np. 1-go gracza z $s:=(GT,GT)$ to $U_{1}((GT,GT))=2$ .

Jeżeli pewna inna strategia $\tilde{s}_{1}$ gracza 1 ma dać wyższą wypłatę, gracz 1 musi zdradzić w pewnej rundzie T+1 po raz pierwszy. Gracz 2 gra strategię grimm–trigger, czyli nie zdradza do T+1, natomiast gra D poczynając od rundy T+2. Najlepsza odpowiedź gracza 1 jest wtedy D we wszystkich kolejnych rundach. Generuje to nastepujący ciąg profili akcji:

$h=((C,C),(C,C),...(C,C),(D,C),(D,D),(D,D),...),$

gdzie $(D,C)$ jest grane w rundzie $T+1$ , oraz ciag wypłat

$(2,2,...,2,,3,1,1,...).$

Znormalizowana wypłata:

$U_{i}(\tilde{s}_{1},GT)=(1-\delta)[2+2\delta+2\delta^{2}+...+2\delta^{{T-1}}+3\delta^{T}+1\delta^{{T+1}}+1\delta^{{T+2}}+...]=2+\delta^{T}-2\delta^{{T+1}}.$

Łatwo widać że dla $s:=GT$

$U_{i}(s,s)\ge U_{i}(\tilde{s},s)\Leftrightarrow\delta\ge 1/2.$

Tak więc, gdy czynnik dyskontowy jest conajmniej 0.5 to para strategii grim–trigger jest RN w nieskończenie powtarzanym (iterowanym) Dylemacie Więźnia z macierzą wypłat $[2,0,3,1]$ .

Uwaga 13.2

Analogiczny rachunek dla ogólnego Dylematu Więźnia daje warunek $\delta\ge\frac{T-R}{T-P}$ na to by para strategii $(GT,GT)$ była RN.

Przykład 13.7

Para strategii $(TFT,TFT)$ jest RN w nieskończenie powtarzanym Dylemacie Więźnia dla dostatecznie dużego czynnika dyskontowego.

Obaj gracze stosując TFT grają w każdej rundzie C i mają w IDW znormalizowane wypłaty równe $R$ każdy. Załóżmy że gracz 2 zmienia strategię. Aby dała ona wyższą wypłatę niż z pary TFT, w pewnej rundzie $T$ gracz 2 musi zagrać D, czyli w $T$ jest grany profil $(C,D)$ . W rundzie $T+1$ gracz 1 gra D i kontynuuje D do rundy w której gracz 2 powraca do C (włącznie z tą rundą). Gracz 2 ma od $T+1$ dwie możliwości: powrót do C lub kontynuowanie D, co daje dwie możliwe strategie: $\tilde{S}_{1}$ , $\tilde{S}_{2}$ . W pierwszym przypadku, czyli gdy w $T+1$ grane jest $(D,C)$ , gracz 1 w $T+2$ gra C, czyli 2 ma taką sytuację jak na początku gry. W drugim gracz 1 kontynuuje D.

W pierwszym przypadku historia ma postać

$h=((C,C),(C,C),...(C,C),(C,D),(D,C),(C,D),...),$

gdzie pierwsze $(C,D)$ jest grane w $T$ . Odpowiadający jej ciąg wypłat gracza 2 w grach pojedynczych to

$(R,R,...,R,T,P,T,...).$

Ponieważ przez pierwsze $T-1$ rund wypłaty gracza 2 pokrywają się z jego wypłatami z pierwotnej strategii TFT, więc przy porównywaniu wypłat za rundę 1 przyjmiemy chwilę $T$ . Znormalizowana wypłata 2 od rundy $T$ ze strategii $\tilde{S}_{1}$ :

$U_{2}(\tilde{S}_{1},TFT)=(1-\delta)[T\delta^{0}+S\delta^{1}+T\delta^{2}+...]=\frac{T}{1+\delta}+\frac{\delta S}{1+\delta}.$

Łatwo widać że

$U_{2}(\tilde{S}_{1},TFT)\le U_{2}(TFT,TFT)=R\Leftrightarrow\delta\ge(T-R)/(R-S).$

W drugim przypadku historia ma postać

$h=((C,C),(C,C),...(C,C),(C,D),(D,D),(D,D),...),$

gdzie $(C,D)$ jest grane w $T$ . Odpowiadający mu ciąg wypłat gracza 2 w grach pojedynczych to

$(R,R,...,R,T,P,P,...).$

Znormalizowana wypłata gracza 2 ze strategii $\tilde{S}_{2}$ od rundy $T$ :

$U_{2}(\tilde{S}_{2},TFT)=(1-\delta)[T+P\frac{\delta}{1-\delta}]=(1-\delta)T+P\delta$

Widać że

$U_{2}(\tilde{S}_{2},TFT)\le U_{2}(TFT,TFT)=R\Leftrightarrow\delta\ge(T-R)/(T-P).$

Identyczne rozumowanie przeprowadzamy dla gracza $1$ . Tak więc, gdy czynnik dyskontowy jest dostatecznie duży, para strategii TFT jest RN w nieskończenie powtarzanym Dylemacie Więźnia.

13.4. Twierdzenia o istnieniu

Dla twierdzeń o istnieniu w grach iterowanych uzywa się też np. nazw: twierdzenia potoczne, ludowe, które biorą się stąd że były one znane od pewnego czasu, a nie są znani ich pierwsi autorzy.

Typowe twierdzenie potoczne mówi że w grze powtarzalnej prawie każdy wynik (ciąg wypłat graczy) może być zrealizowany w pewnej RN, o ile czynnik dyskontowy jest dostatecznie duży. Różne założenia dają różne postacie twierdzenia potocznego.

Definicja 13.7

Gwarantowana wypłata (reservation payoff) w 2-osobowej GN gracza $i$ jest to liczba

$U_{i}^{*}=min_{{S_{{-i}}}}max_{{S_{i}}}U_{i}(S_{i},S_{{-i}}).$

Jest to wypłata jaką $i$ może sobie zagwarantować zakładając że przeciwnik będzie chciał by była ona jak najmniejsza. Na przykład dla IDW gracz AllD ma gwarantowaną wypłatę $P/(1-\delta).$

Definicja 13.8

Procentem (udziałem) kooperacji w zakończonej historii IDW jest to granica

$lim_{{t\rightarrow\infty}}\frac{t_{{CC}}}{t},$

gdzie $t_{{CC}}$ jest liczbą gier pojedynczych do rundy $t$ , w których była grana para akcji $(C,C)$ .

Twierdzenie 13.2

Dla dowolnej liczby $\alpha\in(0,1)$ istnieje, dla dostatecznie dużego czynnika dyskontowego $\delta$ RN w IDW indukująca zakończoną historię $h$ taką że $\alpha$ jest procentem (udziałem) kooperacji w $h$ .

Ćwiczenie 13.1

IDW jako gra jednokrotna

Niech $w\in[0,1)$ oznacza prawdopodobieństwo każdej następnej gry. Niech T oznacza wypłatę w grze jednokrotnej. Wtedy wypłatę ze strategii w której gracz otrzymuje w każdym kroku T definiujemy

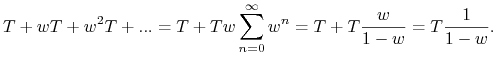$T+wT+w^{2}T+...=T+Tw\sum _{{n=0}}^{\infty}w^{n}=T+T\frac{w}{1-w}=T\frac{1}{1-w}.$

Rozważmy grę 2-osobowa w której każdy z graczy może grać jedną ze strategii: AllD, TFT, z wypłatami $T,R,P,S,\ T>R>P>S$ jednokrotnego Dylematu Więźnia. Macierz wypłat ma postać

	TFT	AllD
TFT	R/(1-w),R/(1-w)	S+Pw/(1-w),P/(1-w)
AllD	T+Pw/(1-w),S+Pw/(1-w)	P/(1-w),P/(1-w)

lub, oznaczając x = w/(1-w):

	TFT	AllD
TFT	R(1+x),R(1+x)	S+Px,T+Px
AllD	T+Px,S+Px	P(1+x),P(1+x)

Oprócz ”nieefektywnej” równowagi Nasha $(AllD,AllD)$ istnieje dla $1>w\ge w_{0}:=\frac{T-R}{T-P}$ symetryczna RN: $(TFT,TFT)$ . Zmienił się typ gry.

W każdej z dwóch RN gracze grają te same akcje.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Teorii Gier