Zagadnienia
3. Równowaga Nasha
3.1. Definicje
Równowaga Nasha (RN) jest centralnym pojęciem teorii gier strategicznych.
Definicja (ważna) 3.1
Profil (strategii mieszanych) gry strategicznej ![]() jest równowagą Nasha wtedy i tylko wtedy jeżeli
jest równowagą Nasha wtedy i tylko wtedy jeżeli
Słownie: żaden z graczy nie może podwyższyć swojej wypłaty przez jednostronną (to znaczy bez zmiany strategii wszystkich innych graczy) zmianę swojej strategii.
W dalszym ciągu udowodnimy ważne twierdzenia charakteryzujące RN.
3.2. Własności RN
Definicja 3.2
Nośnik strategii mieszanej ![]() jest to zbiór
jest to zbiór
![]() akcji (strategii czystych gracza
akcji (strategii czystych gracza ![]() ) taki że akcja o numerze
) taki że akcja o numerze ![]() z
z ![]() należy do
należy do ![]() .
.
INaczej mówiąc nosnik strategii ![]() jest to zbiór strategii czystych które sa grane z dodatnimi
prawdopodobieństwami w danej strategii mieszanej
jest to zbiór strategii czystych które sa grane z dodatnimi
prawdopodobieństwami w danej strategii mieszanej ![]() .
.
Jeżeli używamy dla strategii mieszanej notacji ![]() , to jej nośnik oznaczmy
, to jej nośnik oznaczmy ![]() . Nośnik strategii
czystej jest singletonem. Można wprowadzić dodatkowe charakterystyki strategii: strategie istotnie mieszane
(te które nie są czyste) i całkowicie mieszane (te których nośniki pokrywają się ze odpowiednim zbiorem
strategii czystych).
. Nośnik strategii
czystej jest singletonem. Można wprowadzić dodatkowe charakterystyki strategii: strategie istotnie mieszane
(te które nie są czyste) i całkowicie mieszane (te których nośniki pokrywają się ze odpowiednim zbiorem
strategii czystych).
Twierdzenie 3.1 (O wypłatach strategii czystych w RN)
Niech
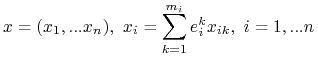 |
- profil strategii mieszanych GS. Ustalmy gracza ![]() . Niech
. Niech ![]() - dwie różne strategie w
- dwie różne strategie w ![]() czyli
czyli ![]() . Wtedy
. Wtedy
| (3.1) |
Tak więc w RN każdy gracz ma jednakowe wypłaty ze wszystkich strategii czystych z nośnika swojej strategii mieszanej którą gra w RN.
Uwaga 3.1
![]() oznacza
oznacza ![]() .
.
ad absurdum. Niech ![]() - RN, oraz
- RN, oraz
| (3.2) |
Definiujemy profil
taki że
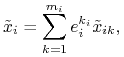 |
gdzie
Pokażemy że
| (3.3) |
czyli sprzeczność z definicją RN. Lewa strona tej nierówności ma postać:
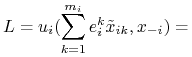 |
(3.4) | |||
| (3.5) |
Prawa strona nierówności
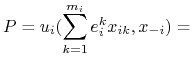 |
(3.6) | |||
| (3.7) |
a zatem z (3.2) otrzymujemy ![]() , czyli (3.3), i.e. sprzeczność z definicją RN.
, czyli (3.3), i.e. sprzeczność z definicją RN.
Wniosek 3.1
Wypłata każdego gracza w RN jest równa jego wypłacie z profilu w którym gracz ten gra dowolną strategią czystą z nośnika swojej strategii w RN, a pozostali gracze grają swoimi strategiami z RN. Mowi o tym
Stwierdzenie 3.1 (O wypłatach w RN)
Niech
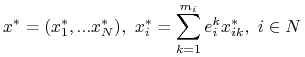 |
- profil strategii mieszanych GS w RN. Wypłata każdego gracza ![]() z profilu
z profilu ![]() jest równa jego
wypłacie z profilu w którym gra (dowolną) strategię czystą z
jest równa jego
wypłacie z profilu w którym gra (dowolną) strategię czystą z ![]() a wszyscy inni nie zmieniają
swych strategii. Formalnie:
a wszyscy inni nie zmieniają
swych strategii. Formalnie:
| (3.8) |
Mówimy, że w RN wypłata gracza jest równa wypłacie z dowolnej granej przez niego w RN strategii czystej.
Gracz ![]() gra w RN pewną strategią
gra w RN pewną strategią ![]()
Korzystając z liniowości ![]() otrzymujemy
otrzymujemy
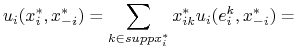 |
(z Twierdzenia 3.1), oznaczając ![]() –numer dowolnej ustalonej strategii z
–numer dowolnej ustalonej strategii z ![]() :
:
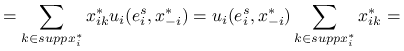 |
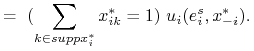 |
Poniżej udowodnimy twierdzenie które pozwala znaleźć RN jeśli jest spełniony warunek dostateczny, oraz daje charakterystykę RN jako warunek konieczny.
![]()
![]() :
:
Warunek 1. jest identyczny z Twierdzeniem 3.1.
Warunek 2.: ad absurdum: w przeciwnym razie mielibyśmy
Z Wniosku (3.1), w RN dla ![]()
a zatem otrzymujemy ![]() , sprzeczność z definicją RN.
, sprzeczność z definicją RN.
![]() :
:
Ustalmy gracza ![]() . Niech
. Niech ![]() będzie jego strategią mieszaną spełniającą warunki 1. i 2. Należy wykazać że
będzie jego strategią mieszaną spełniającą warunki 1. i 2. Należy wykazać że
Oznaczmy, pomijając dla uproszczenia notacji w obu symbolach indeks ![]() :
: ![]() ,
, ![]() - k-ta strategia czysta gracza
- k-ta strategia czysta gracza ![]() . Rozkładając
. Rozkładając ![]() względem nośnika strategii
względem nośnika strategii ![]() i jego dopełnienia otrzymujemy, korzystając z liniowości
i jego dopełnienia otrzymujemy, korzystając z liniowości ![]() :
:
gdzie zastosowaliśmy zapis ![]()
Pierwsza suma po prawej stronie ma (z warunku 1.) postać:
gdzie ![]() jest jedną ze strategii czystych z nośnika
jest jedną ze strategii czystych z nośnika ![]() . Druga suma spełnia (z warunku 2.) nierówność:
. Druga suma spełnia (z warunku 2.) nierówność:
gdzie ![]() jest ustaloną strategią czystą z nośnika
jest ustaloną strategią czystą z nośnika ![]() . Zatem, ponieważ
. Zatem, ponieważ ![]() ,
,
Zauważmy że dla obu profili ![]() oraz
oraz ![]() (każdy profil należy do sympleksu jednostkowego
(każdy profil należy do sympleksu jednostkowego ![]() )
)
a więc
Wykorzystując warunek 1. (do zamiany ![]() na
na ![]() ),
reprezentację
),
reprezentację ![]() i liniowość funkcji wypłat
względem odpowiednich argunentów, przepisujemy wyrażenie po ostatnim znaku równości w postaci
i liniowość funkcji wypłat
względem odpowiednich argunentów, przepisujemy wyrażenie po ostatnim znaku równości w postaci
gdzie ostatnia równość wynika z liniowości wypłat. Otrzymaliśmy więc
Powyższe rozumowanie przeprowadzamy ![]() .
.
Pokażemy przykład zastosowania Twierdzenia LABEL:waz1.
Przykład 3.1
![]()
| L | C | R | |
|---|---|---|---|
| T |
|
3,3 | 1,1 |
| M | 0,0 | 0,0 | 2, |
| B |
|
5,1 | 0, 7 |
![]() . Nastepująca para (profil) strategii mieszanych jest RN:
. Nastepująca para (profil) strategii mieszanych jest RN:
Porównamy wypłaty ze strategii czystych i zastosujemy Twierdzenie LABEL:waz1.
Obliczamy wypłaty ze strategii czystych gdy profil przeciwnika jest z RN. Dla gracza ![]() :
:
Wypłata z ![]()
Wypłata z ![]()
Wypłata z ![]()
Wypłaty ze strategii czystych z ![]() są jednakowe, wypłata z
są jednakowe, wypłata z ![]() jest niższa.
Dla gracza
jest niższa.
Dla gracza ![]() analogiczny rachunek pokazuje że wypłaty ze wszystkich strategii czystych:
analogiczny rachunek pokazuje że wypłaty ze wszystkich strategii czystych: ![]() są równe
są równe ![]() , np:
, np:
Warunki dostateczne na RN (dla drugiego gracza jest potrzebny tylko warunek 1) są więc spełnione.
∎Uwaga: Jeśli w drugim wierszu zamienimy 2 na 3 to powyższy profil nie będzie RN bo
![]()
A oto jeszcze jedna charakterystyka RN dająca w szczególności warunek dostateczny istnienia RN.
Stwierdzenie 3.2
Profil ![]() jest RN
jest RN ![]()
![]()
![]() : Z definicji RN.
: Z definicji RN.
![]() : Ustalmy
: Ustalmy ![]() . Niech
. Niech ![]() - dowolna strategia mieszana gracza
- dowolna strategia mieszana gracza ![]() . Obliczamy: z liniowości
. Obliczamy: z liniowości
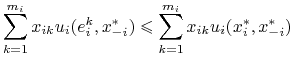 |
(3.9) | |||
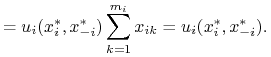 |
(3.10) |
Istotną rolę w teorii gier strategicznych odgrywa ścisła RN.
Definicja 3.3
Profil ![]() jest ścisłą RN (SRN)
jest ścisłą RN (SRN) ![]()
Uwaga 3.2
RN jest SRN gdy strategia każdego gracza w RN jest JEDYNĄ najlepszą odpowiedzią na strategie wszystkich innych graczy w RN (definicja najlepszej odpowiedzi będzie podana w następnym rozdziale).
Mówimy że skończona GS jest generyczna jeśli ![]() funkcja wypłat
funkcja wypłat ![]() jest różnowartościowa.
jest różnowartościowa.
Zachodzi:
Stwierdzenie 3.3
SRN jest RN w strategiach czystych
Wsk. W przeciwnym razie w RN nośnik strategii ![]() pewnego gracza
pewnego gracza ![]() nie jest singletonem.
Z Twierdzenia 3.1 wynika istnienie co najmniej dwóch różnych najlepszych odpowiedzi na
nie jest singletonem.
Z Twierdzenia 3.1 wynika istnienie co najmniej dwóch różnych najlepszych odpowiedzi na ![]() .
.
Uwaga 3.3
SRN nie musi istnieć. Przykład: Gra Orzeł-Reszka.
RN w strategiach czystych nie musi być SRN. Przykład: W grze
| A | B | |
|---|---|---|
| A | 1,1 | 0,0 |
| B | 0,0 | 0,0 |
(A,A) jest SRN, (B,B) nie.
Nawet gdy GS ma dokładnie jedną RN, to ta RN nie musi być SRN. Przykład: w grze
| A | B | C | |
|---|---|---|---|
| D | 1,1 | 1,0 | 0,1 |
| E | 1,0 | 0,1 | 1,0 |
![]() jest (jedyną) RN, ale nie jest SRN.
jest (jedyną) RN, ale nie jest SRN.
Przykład 3.2
W Słabym Dylemacie Więźnia nie ma SRN. To że mieszane strategie nie są SRN wynika ze Stwierdzeniaq 3.3. Bezpośredni rachunek pokazuje że żadna z 3 czystych Rn nie jest SRN.
Definicja 3.4
Profil ![]() w GS w której wszyscy gracze mają ten sam zbiór akcji (
czyli
w GS w której wszyscy gracze mają ten sam zbiór akcji (
czyli ![]() ) jest symetryczną RN jeśli jest RN oraz
) jest symetryczną RN jeśli jest RN oraz ![]()
Uwaga 3.4
”Większość” gier skończonych ma nieparzystą liczbę RN.
Przykładem sa gry 2–osobowe dla których ![]() funkcja
funkcja ![]() jest różnowartościowa (gry generyczne).
jest różnowartościowa (gry generyczne).
Oto ”kontrprzykład”: GS z czterema RN ([33]):
| A | B | C | |
|---|---|---|---|
| D | 0,0 | -1,-1 | -1,-1 |
| E | -1,-1 | -1,-1 | -1,-1 |
| E | -1,-1 | -1,-1 | 0,0 |
(poza trzema czystymi RN jest ”częściowo mieszana” RN ![]() .
.
Innym ”kontrprzykładem” jest gra ”Słaby Dylemat Więźnia”, która jest modyfikacją DW z wypłatą ![]() :
:
| C | D | |
|---|---|---|
| C | R,R | S,T |
| D | T,S | S,S |
dla ![]() . Wypłata każdego gracza nie jest funkcją różnowartośiowa.
Gra ma continuum RN (w tym 3 RN w strategiach czystych), patrz Cwiczenie 4.1.
. Wypłata każdego gracza nie jest funkcją różnowartośiowa.
Gra ma continuum RN (w tym 3 RN w strategiach czystych), patrz Cwiczenie 4.1.
W ekonomicznych zastosowaniach teorii gier istotną rolę odgrywa pojęcie Pareto-optymalności.
Definicja 3.5
Profil gry strategicznej jest Pareto-optymalny (PO) jeżeli nie istnieje profil dający conajmniej jednemu graczowi wyższą, a wszystkim innym conajmniej taką samą wypłatę.
Profil gry jest Pareto-nieoptymalny jeżeli istnieje inny, lepszy dla conajmniej jednego gracza i nie gorszy dla żadnego (czyli gdy nie jest PO).
Przykład 3.3
![]()
| L | S | R | |
|---|---|---|---|
| U | 4,3 | 5,1 | 6,2 |
| M | 2,1 | 8,4 | 3,6 |
| D | 3,0 | 9,6 | 2,8 |
![]() jest RN ale nie jest PO.
jest RN ale nie jest PO. ![]() jest PO, ale nie jest RN.
jest PO, ale nie jest RN.
Przykład 3.4
Gra koordynacyjna
| A | B | |
|---|---|---|
| A | 2,2 |
|
| B |
|
1,1 |
ma 2 RN w strategiach czystych. RN (A,A) jest PO, ale, zakładając wypłaty np. w PLN, nie jest to ”przekonywujący” wybór w praktycznej realizacji.
Przykład 3.5
W 2-osobowym DW profil (C,C) jest PO gdyż gdy jeden z graczy sobie podwyższy wypłatę to wypłata drugiego się obniży. (C,C) jest PO, ale nie jest RN. Profil (D,D) jest RN ale nie jest PO.
W ”Dylemacie Wspólnych Zasobów” (Tragedy of Commons) tzw. minimalna efektywna kooperacja (czyli profil w którym jest dokładnie tylu kooperantów ile wynosi ”próg” - minimalna liczba kooperantów przy której pula jest rozdzielana między wszystkich graczy) jest jedynym profilem PO.
Dla gier o sumie stałej (patrz część 5) każdy profil jest PO (bo nie istnieje profil dający conajmniej jednemu graczowi wyższą, a wszystkim innym conajmniej taką samą wypłatę).
Ćwiczenie 3.1
Pokazać że DW nie ma innych równowag poza (D,D).
W strategiach czystych nie ma innych RN poza (D,D).
Gdyby miał równowagę ściśle mieszaną ![]() , to dla
, to dla ![]() mamy, z twierdzenia podstawowego
mamy, z twierdzenia podstawowego ![]() ,
czyli
,
czyli ![]() , czyli
, czyli ![]() , sprzeczność dla DW. Dla profili w których jeden gracz gra strategią ściśle mieszaną a drugi czystą z twierdzenia–warunku koniecznego na wypłaty z obu strategii czystych pierwszego gracza byłyby jednakowe, co nie jest możliwe dla DW.
, sprzeczność dla DW. Dla profili w których jeden gracz gra strategią ściśle mieszaną a drugi czystą z twierdzenia–warunku koniecznego na wypłaty z obu strategii czystych pierwszego gracza byłyby jednakowe, co nie jest możliwe dla DW.
Ćwiczenie 3.2
Pokaż że w grze w Kota i Myszkę
![]() oraz
oraz ![]() a zatem para strategii
a zatem para strategii ![]() jest RN (w istocie zachodzą równości).
jest RN (w istocie zachodzą równości).
Ćwiczenie 3.3
Ogólniejsza postać gry ”W Kota i Myszkę”
| L | P | |
|---|---|---|
| L | 0,K | M,0 |
| P | M,0 | 0,K |
Obliczyć średnie wypłaty przy stosowaniu strategii mieszanych i znależć RN.
Ćwiczenie 3.4
W grze
| L | S | R | |
|---|---|---|---|
| U | 0,1 | 0,1 | 2,4 |
| M | 5,1 | 2,2 | 1,0 |
| D | 4,3 | 1,4 | 1,0 |
znależć RN i profile PO w strategiach czystych.
Odp.: (U,R): RN, PO. (M,S):RN ale nie PO. (D,L):PO ale nie RN.
Ćwiczenie 3.5
Znaleźć RN w grze
| L | S | R | |
|---|---|---|---|
| U | 1,3 | 1,3 | 1,3 |
| M | 0,0 | 2,2 | 2,2 |
| D | 0,0 | 0,0 | 3,1 |
Ćwiczenie 3.6
GS jest o sumie zerowej jeżeli ![]() .
Wykaż że dla GS o sumie zerowej każdy profil jest PO.
.
Wykaż że dla GS o sumie zerowej każdy profil jest PO.




