Zagadnienia

7.1 Wprowadzenie
7.2 Scenariusz ewolucyjny. Gra Jastrząb-Gołąb
7.3 Dynamika replikatorowa
7.4 Strategia ewolucyjnie stabilna

7. Gry ewolucyjne

7.1. Wprowadzenie

Początki teorii gier ewolucyjnych (TGE) sięgają lat 60ych XX wieku. Pierwotnie TGE rozwijała się w oparciu o idee i przykłady wzięte z biologii. Zasadniczym jej elementem bylo spostrzeżenie że biologiczne przystosowanie (fitness) gatunków zależy od interakcji które można opisać językiem teorii gier. Gracze (osobniki, geny) nie zmieniali swych strategii (np. cech w jakie geny wyposażają organizm, przykładowo gresywna, pokojowa), nie musieli wiedziec że graja w grę, a zmiana udziału strategii w populacji brała się z różnego tempa reprodukcji graczy używajacych poszczególonych strategii. W tym kontekście TGE jest związana z darwinowska teoria ewolucji, której jednym z podstawowych postulatów jest założenie że udział procentowy osobników o lepszym przystosowaniu rośnie w populacji.

J. Maynard Smith jako pierwszy w latach 60ych zaproponował wyjaśnianie zachowań zwierząt za pomocą teorii gier. O ile w interakcjach międzyludzkich gracze, agenci, to ludzie, zespoły, instytucje, mający świadomośc uczestniczenia w grze, o tyle w przypadku świata zwierzęcego, ogólniej w biologii, opisywane obiekty nie mają świadomości uczestnictwa w interakcjach które nazywamy teoriogrowymi, nie mają świadomości podejmowania decyzji, i idea opisu takich interakcji za pomocą formalizmu teorii gier miała w owym czasie charakter rewolucyjny. Jedną z inspiracji leżących u źródeł TGE były obserwacje konfliktów w świecie zwierzęcym, np. walk rytualnych, walk o terytorium, o samicę, czy o przewodnictwo w stadzie.

W naukach biologicznych powstały odrębne działy wykozystujące formalizm teorii gier, takie jak biologia ewolucyjna, ekologia ewolucyjna, patrz np. [3]. Rozwijają sie zastosowania TGE w ekonomii, patrz np. [15, 33, 26], w psychologii i w naukach społecznych. W ekonomii gracze to podmioty gospodarcze, wypłaty to zyski, a strategie to np. sposoby działania na rynku. W naukach społecznych stosuje się TGE w szczegolności do opisu, powstawania i utrzymywania się postaw kooperacyjnych i altruistycznych w społeczeństwach (ludzi, zwierzat), do opisu powstawania i ewolucji norm społecznych.

O ile w biologii czestości strategii zależą od temp reprodukcji, a mutacje mają podłoże genetyczne, to w naukach społecznych i w ekonomii zależą od możliwości imitacji jednych graczy przez drugich, oraz od możliwości indywidualnego i grupowego uczenia się (learning), a mutacje to np. eksperymenty, innowacje, przypadkowe błędy czy zachowania idiosynkratyczne. W ekonomii, naukach behawioralnych, stosujemy równania dynamiki imitacji, dynamiki najlepszej odpowiedzi, dynamiki wielokrotnego testowania i inne. Będzie to tematem wykładu XV.

Podstawowym pojęciem klasycznej TG jest równowaga Nasha. TG w zasadzie nie precyzuje czy, i która (gdy jest więcej niż jedna) RN jest grana, osiągana, i jeżeli gracze grają RN, to jak do niej doszli. Teoria Gier Ewolucyjnych (TGE) próbuje odpowiedzieć na te pytania. Podejście ewolucyjne polega na opisie jak zachodzą zmiany składu takich układów, jakie są stany asymptotyczne procesów ewolucyjnych, jaka jest ich stabilność itp.

Równania rozpadu promieniotwórczego i reprodukcji

Niech $N(t)$ oznacza liczbę obiektów pewnego typu w układzie w chwili $t$ . Dla małych przyrostów czasu $\delta$ postulujemy równanie reprodukcji:

$N(t+\delta)=N(t)+a\delta N(t),\quad N(0)=N_{0}.$

Dla $\delta\rightarrow 0$ otrzymujemy równanie ewolucji

$N^{{\prime}}(t)=aN(t)==>N(t)=N_{0}\exp(at)$

$a>0$ - stała wzrostu, tempo wzrostu, wyraża sie więc wzorem

$a=N^{{\prime}}(t)/N(t)$

W fizyce cząstek elementarnych rozważa sie analogiczne równanie rozpadu promieniotwórczego. Niech $N(t)$ oznacza masę cząstek elementarnych które nie uległy rozpadowi do czasu $t$ . Załóżmy że dla bardzo małych czasów $\delta$

$N(t+\delta)=N(t)-\lambda\delta N(t),\quad N(0)=N_{0},$

gdzie $\lambda>0$ - stała rozpadu promieniotwórczego. Dla $\delta\rightarrow 0$ otrzymujemy różniczkowe równanie rozpadu promieniotwórczego

$N^{{\prime}}(t)=-\lambda N(t)==>N(t)=N_{0}\exp(-\lambda t)$

7.2. Scenariusz ewolucyjny. Gra Jastrząb-Gołąb

Podstawowy scenariusz ewolucyjny:

Podstawowy scenariusz ewolucyjny jest to eksperyment myślowy, wywód teoretyczny:

1. rozpatrujemy dużą populacja jednakowych graczy

2. każdy posiada jedną, niezmienną strategię

3. zakładamy łączenie losowe w pary, w parach jest jednorazowo rozgrywana 2-osobowa gra symetryczna

4. każdy gracz rodzi potomstwo (reprodukcja aseksualna), wypłata z gry jest to liczebność potomstwa.

5. potomstwo dziedziczy strategię rodzica.

6. wracamy do p. 1.

Uwaga 7.1

Bardziej skomplikowane scenariusze ewolucyjne uwzględniaja np. gry wieloosobowe, zmiany strategii przez graczy, błędy w wyborze optymalnych strategii, wprowadzają nielosowe oddziaływania (selekcja grupowa, dobór krewniaczy, sygnalny itp.)

Gra ewolucyjna jest to gra strategiczna rozgrywana w populacji osobników zgodnie z scenariuszem ewolucyjnym.

Przykład 7.1

Rozważmy dużą populację składajacą się z osobników 2 typów: A i B. Załóżmy dla uproszczenia że osobniki nie wymierają, liczba osobników każdego typu rośnie w wyniku pewnego procesu, które nazwiemy reprodukcją, procesem urodzin. Niech będzie w danej chwili $t$ $N_{A}>0$ osobników A i $N_{B}$ osobników B, $N:=N_{A}+N_{B}$ .

Zakładamy że liczba nowych osobników typu A która powstaje w czasie pomiędzy $t$ a $t+\Delta t,\ \ \Delta t\ll 1$ jest wprost proporcjonalna do $N_{A}(t)$ oraz do $\Delta t$ . Współczynnik proporcjonalności oznaczamy $a$ i nazywamy tempem urodzin (birth rate) osobników typu A. Tempo urodzin $a$ osobników typu A jest więc liczbą nowych osobników typu A powstających w jednostce czasu $\Delta t$ przypadających na jednego ”starego” A, analogicznie $b$ - liczba nowych osobników typu B na jednego ”starego” B w $\Delta t$ . Formalnie $N_{A}(t+\Delta t)-N_{A}(t)=aN_{A}(t)\Delta t,$ a zatem w granicy

$a=\frac{N_{A}^{{{}^{{\prime}}}}}{N_{A}}.$

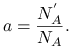Wzór ten możemy przyjąć za definicję tempa urodzin dla odpowiednio gładkich funkcji (w dużych populacjach zamiast liczby osobników danego typu rozważamy ich masę). Niech $f_{A}(t):=N_{A}/N$ oznacza ułamek (częstość, proporcję, udział) osobników A w populacji w chwili $t$ . W czasie $\Delta t$ powstaje $aN_{A}\Delta t$ osobników typu A i $bN_{B}\Delta t$ osobników typu B. Po upływie $\Delta t$ w populacji będzie więc $N_{A}+aN_{A}\Delta t$ osobników A oraz $N_{B}+bN_{B}\Delta t$ osobników B. Częstość osobników A będzie równa:

$f_{A}(t+\Delta t)=\frac{N_{A}+aN_{A}\Delta t}{N+aN_{A}\Delta t+bN_{B}\Delta t}$

Jak łatwo obliczyć,

$f_{A}(t+\Delta t)>f_{A}(t)\Leftrightarrow a>b.$

Otrzymaliśmy intuicyjnie oczywisty

Wniosek 7.1

Częstość graczy A rośnie gdy tempo urodzin osobników A jest większe od tempa urodzin B.

Podstawową rolę w prezentacji podstaw ewolucyjnej teorii gier będzie miala gra Jastrząb–Gołąb.

Gra Jastrząb–Gołąb. n=2 identyczne osobniki wchodzą w konflikt o pewne dobro, np. terytorium, o wartości $v>0$ . Niech $c>v$ będzie kosztem walki. Każdy gracz ma do wyboru 2 strategie czyste (akcje): strategia Jastrzębia (J) i strategia Gołębia (G). Macierz wypłat:

	J	G
J	$\frac{v-c}{2},\frac{v-c}{2}$	$v,0$
G	$0,v$	$\frac{v}{2},\frac{v}{2}$

Gra ma 2 ”czyste” RN: $(J,G),(G,J)$ i mieszaną RN $((v/c,1-v/c),(v/c,1-v/c)).$

Rozważamy scenariusz ewolucyjny z grą Jastrząb–Gołąb. Mamy dużą populację składającą się z osobników A=J, i B=G, o częstościach odpowiednio p i 1-p, których losowo łączymy w pary w każdej jednostce czasu. Każda para rozgrywa jedną grę Jastrząb-Gołąb. Chcemy opisać jak będzie ewoluował skłąd procentowy Jastrzębi i Gołębi w populacji. Niech $p=p(t)$ oznacza częstość Jastrzębi w chwili $t$ .

Średnie wypłata osobników grających J i G w chwili $t$ wynoszą odpowiednio

$W_{J}=p(v-c)/2+(1-p)v,\ \ W_{G}=p\cdot 0+(1-p)v/2.$

Założenie ze scenariusza ewolucyjnego, że wynikiem gry sa wypłaty w grze są mierzone liczebnością potomstwa, (dziedziczącego strategię rodzica) odpowiada paradygmatowi teorii Darwina: przystosowanie (fitness) jest mierzone liczebnością potomstwa. Teoriogrowym odpowiednikiem przystosowania jest wypłata. Założenie to formalnie formułujemy jako postulat:

Tempa urodzin $a,b$ są liniowymi funkcjami średnich wypłat osobników J, G:

$a=W_{0}+W_{J},\ \ b=W_{0}+W_{G},$

gdzie $W_{0}$ jest stałym, niezależnym od interakcji tempem urodzin (baseline fitness), który dodajemy by uniknąć ujemnych temp urodzin. Zauważmy że w przeciwieństwie np. do rozpadu promieniotwórczego, tempa urodzin są (przez zależność od składu populacji) zależne od czasu. Otrzymujemy

$a-b=W_{J}-W_{G}=\frac{c}{2}(p^{*}-p),\quad p^{*}:=\frac{v}{c}.$

W szczególności, jeżeli $p$ – częstość J w danej chwili jest niższa od $p^{*}$ (i różna od zera), to częstość J rośnie w procesie ewolucyjnym. Analogicznie, jeżeli $p>p^{*},\ \ p\neq 1$ , to częstość J maleje. dla $p=p^{*}$ nie zmienia się. Oznacza to że skład procentowy populacji dąży do $p^{*}=\frac{v}{c}$ niezależnie od składu początkowego [o ile $p(0)\in(0,1)$ , wpp. populacja składa się cały czas tylko z graczy G lub tylko z graczy J]. Wartość $p^{*}$ można więc nazwać stanem równowagi. Populacja J-G o równowagowym składzie $p^{*}=v/c$ nie zmienia składu w scenariuszu ewolucyjnym. Odchyłka procentowego udziału każdego typu od składu równowagowego uruchamia ewolucję do składu równowagowego.

Powyższy model ewolucyjny przestawimy w języku rownań różniczkowych. Niech $N(t)$ - liczebność układu w $t$ , $p=p(t)$ –częstość strategii J, $a=a(t),b=b(t)$ - tempa urodzin odpowiednio graczy J, G. W czasie $\Delta t\ll 1$ urodzi się w przybliżeniu $a\Delta tp(t)N(t)$ Jastrzębi, $b\Delta t(1-p(t))N(t)$ Gołębi. Tempo zmiany $p$ :

$\frac{p(t+\Delta t)-p(t)}{\Delta t}=\frac{cp(1-p)(p^{*}-p)}{2[1+ap\Delta t+b(1-p)\Delta t]},$

(7.1)

gdzie $p^{*}:=v/c$ . Dla $\Delta t\rightarrow 0$ otrzymujemy równanie różniczkowe ewolucji częstości Jastrzębi

$\frac{dp(t)}{dt}=\frac{c}{2}p(1-p)(p^{*}-p).$

(7.2)

Punkty $p=p^{*}$ , $p=0$ i $p=1$ są punktami stałymi (punktami równowagowymi) powyższej dynamiki w omawianym scenariuszu ewolucyjnym. Pierwszy z nich jest atraktorem, dwa pozostałe to repellery.

Uwaga 7.2

Do liczenia średnich wypłat są równoważne scenariusze:

1. Duża populacja graczy: $x$ : częstość grających J, $1-x$ : częstość G, każdy gra stale swoja strategią

2. Duża populacja graczy, każdy gra z prawdopodobieństwem $x$ strategię J, a z prawdopodobieństwem $1-x$ strategię G.

3. Duża populacja graczy, osobniki grają różne strategie mieszane, ale średnio w każdej chwili czasu w $x$ wszystkich gier jest grana strategia J, w $1-x$ gier–strategia G.

7.3. Dynamika replikatorowa

Model dynamiki replikatorowej jest podstawowym i najbardziej znanym różniczkowym modelem TGE.

Rozważamy scenariusz ewolucyjny: GS: $<\{ 1,2\},A_{i},u_{i}>,\ \ i=1,...n,$ $n$ - liczba strategii czystych,

$N_{i}(t)$ - liczba (masa) graczy grających strategią $i$ (masa podpopulacji $i$ ),

$N(t)=\sum _{{i=1}}^{{n}}N_{i}(t)$ - liczebność populacji (masa całej populacji),

$x_{i}=x_{i}(t)=N_{i}/N$ –częstość graczy grających $i$ , częstość strategii $i$ ,

$x=(x_{1},x_{2},...x_{n})=\sum _{{k=1}}^{{n}}e^{k}x_{k}\in\Delta,$ - stan populacji w chwili $t$ , $e^{k}$ - k-ty wersor w $\Re^{n},\ \Delta$ - sympleks jednostkowy. Gracze są nierozróżnialni, więc wersor ma tylko jeden indeks (ogólnie mieliśmy $e_{i}^{k}$ - k-ty wersor gracza i-tego).

$u(e^{i},x)$ –wypłata strategii $i$ gdy populacja jest w w stanie $x$ . Jest to z definicji wartość oczekiwana zmiennej losowej–wypłaty gracza grającego strategią $i$ z losowym partnerem z populacji w stanie $x$ (i.e. $x$ jest rozkładem tej zmiennej losowej); $x_{k}$ jest prawdopodobieństwem wylosowania gracza grającego strategią $k,\ k=1,...n$ ). Równoważnie można powiedzieć że jest to wypłata gracza grającego $i$ z losowo wybranym partnerem grającym strategią mieszaną $x$ .

$u(x,x)=\sum _{{i=1}}^{n}x_{i}u(e^{i},x)$ - średnia wypłata w populacji (średnia wypłata losowego gracza).

Uwaga 7.3

W ogólniejszym przypadku gier k-osobowych $u(e^{i},x)$ jest wartością oczekiwaną zmiennej losowej–wypłaty gracza grającego strategią $i$ z $k-1$ losowo wybranymi partnerami z populacji w stanie $x$ .

K. Darwin: udział procentowy osobników (czyli strategii) o lepszej adaptacji rośnie w wyniku doboru naturalnego (”lepsza adaptacja” $\equiv$ wyższe tempo urodzin $\equiv$ wyższa średnia wypłata).

W rozważanym scenariuszu ewolucyjnym postulat ten formalizujemy w następujący sposób:

Tempo wzrostu liczby osobników grających strategię $i$ w populacji w stanie $x$ jest proporcjonalne (u nas–dla uproszczenia–równe) do wypłaty strategii $i$ gdy populacja jest w stanie $x$ .

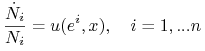$\frac{\dot{N}_{i}}{N_{i}}=u(e^{i},x),\quad i=1,...n$

Obliczamy

$N_{i}=x_{i}N,\ \ \dot{N}_{i}=\dot{x}_{i}N+x_{i}\dot{N},\ \ N\dot{x}_{i}=\dot{N}_{i}-x_{i}\dot{N},$

$N\dot{x}_{i}=u(e^{i},x)N_{i}-x_{i}\sum _{j}u(e^{j},x)N_{j}=$

$=u(e^{i},x)N_{i}-x_{i}\sum _{j}u(e^{j},x)x_{j}N=u(e^{i},x)x_{i}N-x_{i}Nu(x,x).$

Dzieląc przez $N$ otrzymujemy

Równania Dynamiki Replikatorowej (RDR)

$\dot{x}_{i}(t)=x_{i}[u(e^{i},x)-u(x,x)],\quad i=1,...n.$

Słownie: tempo zmiany $\dot{x}_{i}/x_{i}$ udziału (częstości) i-tej strategii w populacji jest różnicą między wypłatą strategii $i$ a średnią wypłatą w stanie populacji $x$ . Częstości strategii o wypłatach powyżej (poniżej) średniej rosną (maleją).

Przypomnijmy że w podstawowym scenariuszu ewolucyjnym gracze grają w symetryczną grę dwuosobową o macierzy wypłat $A$ . Mamy więc

$u(e^{i},x)=(Ax)_{i},\quad u(x,x)=\sum x_{i}(Ax)_{i}\equiv xAx,$

(7.3)

RDR przyjmuja postać

$\dot{x}_{i}(t)=x_{i}[(Ax)_{i}-xAx],\quad i=1,2,...n,$

gdzie $A$ jest macierzą wypłat rozważanej symetrycznej GS.

Uwaga 7.4

$\$

Udział strategii o wyższej wypłacie rośnie, patrz Ćwiczenie 7.1.
Sympleks jednostkowy $\Delta$ jest inwariantny względem RDR, patrz Ćwiczenie 7.2.
Jeżeli do tempa wzrostu 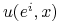$u(e^{i},x)$ dodamy jednakową dla wszystkich strategii stałą, którą interpretujemy jako różnicę między stałym tempem urodzin i śmierci, to RDR nie ulegną zmianie, patrz Ćwiczenie 7.3.
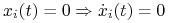Strategia nieobecna pozostaje nieobecna: $x_{i}(t)=0\Rightarrow\dot{x}_{i}(t)=0$ .
Dla 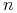$n$ strategii otrzymujemy 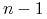$n-1$ niezależnych równań różniczkowych z prawymi stronami będącymi wielomianami których stopień zależy od rzędu gry. Dla gier wieloosobowych stosujemy zamiast (7.3) definicję wypłaty jako wartości oczekiwanej. Wypłata danej strategii jest wielomianem wyższego stopnia. Dla gier k-osobowych jest to w ogólności wielomian stopnia 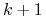$k+1$ .
RDR otrzymuje się też w modelach w których zmiana strategii następuje w wyniku imitacji strategii o lepszym przystosowaniu, patrz np. [11, 39] i literatura cytowana w tych monografiach.

Przykład 7.2

Gra ewolucyjna z dwiema strategiami: $x=(x_{1},x_{2}),x_{2}=1-x_{1}$ . Dla gry wieloosobowej z dwiema strategiami mamy

$\dot{x}_{1}(t)=x_{i}(1-x_{i})[u(e^{1},x)-u(e^{2},x)].$

W szczególnym przypadku gry dwuosobowej z macierzą wypłat $A$ otrzymujemy

$\dot{x}_{1}(t)=x_{1}[(Ax)_{1}-xAx]=x_{1}[(Ax)_{1}-(x_{1},x_{2})((Ax)_{1},(Ax)_{2})]$

$=x_{1}[(Ax)_{1}-x_{1}(Ax)_{1}-x_{2}(Ax)_{2}]=x_{1}(1-x_{1})[(Ax)_{1}-(Ax)_{2}].$

Dla HD: $\ A=[(v-c)/2,v,0,v/2],\quad(Ax)_{1}=x_{1}(v-c)/2+v(1-x_{1}),\ (Ax)_{2}=(1-x_{1})v/2,$

$\dot{x}_{1}(t)=cx_{1}(1-x_{1})(v/c-x_{1})/2$

Dla PD: $\ A=[3,1,4,2],\quad(Ax)_{1}=3x_{1}+1(1-x_{1}),\ (Ax)_{2}=4x_{1}+2(1-x_{1}),$

$\dot{x}_{1}(t)=x_{1}(1-x_{1})(0\cdot x-1).$

RDR mają ciekawe własności matematyczne. Udowodnimy interesujące twierdzenie łaczące ”statyczne” pojęcie równowagi Nasha z ”dynamicznym” pojęciem punktu krytycznego (punktu stałego) RDR.

Definicja 7.1

W grach symetrycznych 2-osobowych profil $\hat{x}$ gracza jest strategią Nasha jeżeli $(\hat{x},\hat{x})$ jest RN.

Twierdzenie 7.1 (Strategia Nasha–punktem stałym RDR)

Jeżeli $\hat{x}=(\hat{x}_{1},\hat{x}_{2},...,\hat{x}_{n})$ jest strategią Nasha w dwuosobowej symetrycznej GS o $n\times n$ macierzy wypłat $A$ , to $\hat{x}$ jest punktem stałym RDR

$\dot{x}_{i}=x_{i}[(Ax)_{i}-xAx],\ \ i=1,...n.$

Niech $\hat{x}=(\hat{x}_{1},\hat{x}_{2},...,\hat{x}_{n})$ będzie strategią Nasha. Dla $\hat{x}_{i}=0$ mamy $\dot{\hat{x}}_{i}=0$ . Dla $\hat{x}_{i}\ne 0$ z Twierdzenia 3.1 (o wypłatach strategii czystych w RN) wynika istnienie stałej $c$ takiej że

$\forall i:\ \hat{x}_{i}\neq 0\quad u(e^{i},\hat{x})=c.$

Zauważmy że $u(e^{i},\hat{x})=(A\hat{x})_{i}$ , a zatem

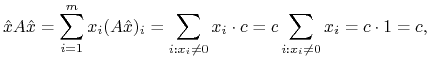$\hat{x}A\hat{x}=\sum _{{i=1}}^{m}x_{i}(A\hat{x})_{i}=\sum _{{i:x_{i}\neq 0}}x_{i}\cdot c=c\sum _{{i:x_{i}\neq 0}}x_{i}=c\cdot 1=c,$

a zatem $\dot{x}_{i}=x_{i}(c-c)=0$ .

∎

Oto kilka innych interesujących zależności między powyższymi pojęciami. Scisłe sformułowania i dowody tych i innych ciekawych faktów wiążących strategie Nasha i punkty krytyczne RDR można znależć np. w monografiach [11, 39].

Twierdzenie 7.2

$\$ Dla gier symetrycznych

Stabilne w sensie Liapunowa (neutralnie stabilne) punkty krytyczne RDR są strategiami Nasha.

Strategie Nasha będące ESS (patrz kolejny podrozdział) są lokalnie asymptotycznie stabilnymi punktami krytycznymi RDR.

Udział strategii ściśle zdominowanej maleje do zera w dynamice replikatorowej.

7.4. Strategia ewolucyjnie stabilna

John Maynard Smith w latach 1970-ych wprowadził pojęcie strategii ewolucyjnie stabilnej (ESS), uzupełniając warunek rownowagi Nasha o dodatkowy warunek stabilności. ESS odgrywa w TGE porównywalną rolę do Równowagi Nasha w klasycznej TG. Nieformalnie ESS jest to taki profil populacji, który jest odporny na inwazję (dostatecznie) małej grupy mutantów o odmiennym fenotypie. Fenotyp to np. cecha budowy ciała (wielkość osobnika, kolor skóry), agresja, altruizm, sygnał wysyłany innym zwierzęciom itp. Fenotypy są dziedziczone.

Uwaga 7.5

Do istotnych osiągnięć ESS należy wytłumaczenie dlaczego na ogół rodzi się mniej więcej tyle samo samców co samic. Okazuje się że strategia rodzenia samców i samic z jednakowym prawdopodobieństwem jest–w odpowiednim formaliźmie teoriogrowym–jedyną strategią ewolucyjnie stabilną.

Definicja (ważna) 7.2 (Maynard Smith, Price, 1973)

W symetrycznej 2–osobowej grze ewolucyjnej strategia $\hat{\sigma}$ jest ewolucyjnie stabilna (ESS–Evolutionarily Stable Strategy) jeżeli $\forall\sigma\neq\hat{\sigma}\ \exists\epsilon _{0}>0$ takiego że dla $\epsilon\in(0,\epsilon _{0}]$ zachodzi

$\hat{\sigma}A[(1-\epsilon)\hat{\sigma}+\epsilon\sigma]>\sigma A[(1-\epsilon)\hat{\sigma}+\epsilon\sigma].$

$\epsilon _{0}$ nazywamy barierą inwazyjną.

Uwaga 7.6

$\sigma _{1}A\sigma _{2}\equiv u_{1}(\sigma _{1},\sigma _{2}).$

Twierdzenie 7.3 (Maynard Smith, 1982)

Strategia $\hat{\sigma}$ jest ESS w populacji graczy łączonych losowo w pary rozgrywające symetryczną grę 2-osobową $\Leftrightarrow$

$(i)\ \ \forall\sigma\in\Sigma,\ \hat{\sigma}A\hat{\sigma}\ge\sigma A\hat{\sigma};$

$(ii)\ \ \forall\sigma\in\Sigma:\sigma\neq\hat{\sigma},\ \hat{\sigma}A\hat{\sigma}=\sigma A\hat{\sigma}\Rightarrow\hat{\sigma}A\sigma>\sigma A\sigma.$

(i) to warunek RN, (ii)–warunek ”stabilności”. Gdyby (ii) nie było spełnione, strategia $\sigma$ mogłaby ”opanować” populację $\hat{\sigma}$ w wyniku neutralnego dryfu.

Tak więc strategia $\hat{\sigma}$ jest ewolucyjnie stabilna jeżeli 1. $\hat{\sigma}$ jest najlepszą odpowiedzią na siebie [a zatem profil $(\hat{\sigma},\hat{\sigma})$ jest RN]. 2. jeżeli inna strategia $\sigma$ jest najlepszą odpowiedzią na $\hat{\sigma}$ to $u(\hat{\sigma},\sigma)>u(\sigma,\sigma)$ , czyli granie $\hat{\sigma}$ przeciwko $\sigma$ daje wyższą wypłatę niż $\sigma$ przeciwko $\sigma$ . Jeżeli śladowe ilości mutantów grają $\sigma$ w populacji grającej $\hat{\sigma}$ , to ich udział w populacji maleje do zera.

Przepiszmy definicję ESS w postaci

$(1-\epsilon)(\hat{\sigma}A\hat{\sigma}-\sigma A\hat{\sigma})+\epsilon(\hat{\sigma}A\sigma-\sigma A\sigma)>0.$

(7.4)

$\Leftarrow$ :

Jeśli $\hat{\sigma}A\hat{\sigma}>\sigma A\hat{\sigma},$ to 7.4 zachodzi dla $\epsilon$ dostatecznie małych.

Jeśli $\hat{\sigma}A\hat{\sigma}=\sigma A\hat{\sigma},$ to 7.4 wynika z (ii).

$\Rightarrow$

Ad abs. Niech $\hat{\sigma}$ nie spełnia (i), i.e. $\exists\sigma:\hat{\sigma}A\hat{\sigma}<\sigma A\hat{\sigma}.$ Wtedy

$\forall\epsilon\in(0,1)\quad(1-\epsilon)(\hat{\sigma}A\hat{\sigma}-\sigma A\hat{\sigma})<0.$

Dla dostatecznie małego $\epsilon$ wyrażenie po lewej stronie nierówności (7.4) jest więc ujemne, sprzeczność.

Niech $\hat{\sigma}$ nie spełnia (ii). Wtedy $\exists\sigma\neq\hat{\sigma}:$

$\hat{\sigma}A\hat{\sigma}=\sigma A\hat{\sigma}\ \ \mbox{i}\ \ \hat{\sigma}A\sigma\le\sigma A\sigma.$

Wtedy lewa strona (7.4) jest mniejsza lub równa zero, sprzeczność.

∎

Natychmiastową konsekwencją tego twierdzenia jest

Wniosek 7.2

Jeżeli $\hat{\sigma}$ jest ESS to profil $(\hat{\sigma},\hat{\sigma})$ jest (symetryczną) RN.

Wniosek 7.3

Jeżeli profil $(\hat{\sigma},\hat{\sigma})$ jest ścisłą RN, to $\hat{\sigma}$ jest ESS.

Przykład 7.3

Pokażemy że $\hat{p}:=(v/c,1-v/c)$ jest ESS w grze HD z macierzą wypłat $A$ :

	J	G
J	$\frac{v-c}{2},\frac{v-c}{2}$	$v,0$
G	$0,v$	$\frac{v}{2},\frac{v}{2}$

Dla uproszczenia przyjmiemy $v=2,c=4$ , a zatem $\hat{p}=(1/2,1/2)$ . Niech $p=(x,1-x)\neq\hat{p}$ –dowolna inna strategia. Obliczamy

$\hat{p}A\hat{p}=pA\hat{p},$

a zatem warunek równowagi (i) jest spełniony. Warunek stabilności sprowadza się do wykazania że $\hat{p}Ap>pAp.$ Obliczamy:

$\hat{p}Ap-pAp=(\hat{p}-p)Ap=2(x^{2}-x+\frac{1}{4})>0\ dla\ x\neq\frac{1}{2}.$

Uwaga 7.7

Powyższy rezultat wynika też z twierdzenia, które podajemy bez dowodu.

Twierdzenie 7.4

Strategia $\hat{\sigma}$ jest ESS $\Leftrightarrow$ dla wszystkich $\sigma\neq\hat{\sigma}$ z pewnego jej otoczenia zachodzi nierówność

$\hat{\sigma}A\sigma>\sigma A\sigma.$

Dla gry HD (7.4) i strategii $\hat{\sigma}=(v/c,1-v/c)$ obliczamy $\hat{\sigma}A\sigma-\sigma A\sigma=\frac{1}{2c}(v-cx)^{2}>0$ dla $x\neq\frac{v}{c}$ .

Jedną z wad pojęcia ESS jest fakt że nie dla wszystkich klas gier ważnych w teorii i w zastosowaniach ESS istnieje.

Przykład 7.4

W grze Kamień-Papier-Nożyczki, z macierzą wypłat

	K	P	N
K	0,0	-1,1	1,-1
P	1,-1	0,0	-1,1
N	-1,1	1,-1	0,0

jedyna RN jest strategia mieszana $\sigma^{*}=(1/3,1/3,1/3)$ . Jest to więc jedyny kandydat na ESS. Niech $\sigma=(1,0,0)$ będzie czystą strategią (Kamień). Mamy

$\sigma^{*}A\sigma^{*}=\sigma A\sigma^{*}(=0).$

$\sigma^{*}A\sigma=\sigma A\sigma=0,$

Warunki te są sprzeczne z częścią $(ii)$ Twierdzenia 7.3, a zatem $\sigma^{*}$ nie jest ESS, a ponieważ $\sigma^{*}$ była jedynym kandydatem, więc ESS nie istnieje.

Ćwiczenie 7.1

Pokaż że jeżeli $u(e^{j},x)>u(e^{i},x)$ , to $\frac{d}{dt}\frac{x_{j}}{x_{i}}>0$

Ćwiczenie 7.2

Pokaż inwariantność sympleksu jednostkowsego względem RDR. Wsk.: wysumuj RDR po wszystkich strategiach i skorzystaj z jednoznaczności rozwiązania odpowiedniego zagadnienia Cauchy'ego.

Ćwiczenie 7.3

Niech tempo urodzin graczy o strategii $i$ wynosi $\beta+u(e^{i},x)$ , gdzie $\beta$ jest stała. Pokaż że RDR nie ulegają zmianie.

Ćwiczenie 7.4

RDR dla SD:

$A=[3,2,4,1]\quad(Ax)_{1}=3x_{1}+2(1-x_{1}),\ (Ax)_{2}=4x_{1}+1(1-x_{1}),$

$\dot{x}_{1}(t)=x_{1}(1-x_{1})(1-2x_{1}).$

Ćwiczenie 7.5

Rozważmy grę

	A	B
A	2,2	0,0
B	0,0	0,0

w scenariuszu ewolucyjnym. Pokazać że z dwóch strategii Nasha $A$ jest ESS, $B$ nie.

Ćwiczenie 7.6

Omówić Twierdzenie 7.1 dla słabego Dylematu Więźnia (napisać RDR, strategie Nasha itp.).

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Teorii Gier