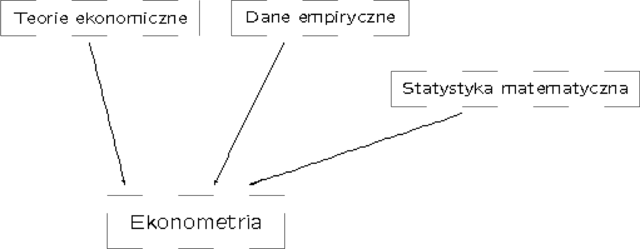
W skrócie można powiedzieć, że ekonometria to zestawienie danych empirycznych z teoriami ekonomicznymi przy zastosowaniu statystyki matematycznej.

Podstawowe cele ekonometrii to:
1. Analiza danych empirycznych i prognozowanie na ich podstawie;
2. Weryfikacja i kalibrowanie teorii ekonomicznych.

Kluczowym obiektem w ekonometrii jest tzw. model ekonometryczny. Zapisujemy go w postaci

gdzie t∈N zwykle oznacza czas – kolejny moment lub kolejny przedział czasowy (dzień, miesiąc, rok …), ale może też oznaczać numer porządkowy obserwacji (np. firmy, której dotyczą dane czy województwa).
Xt∈Rk to wektor zmiennych objaśniających,
Yt∈Rm to wektor zmiennych objaśnianych,
F nazywa się postacią analityczną modelu, jest to funkcja o wartościach w Rm;
a εt nazywa się składnikiem losowym.

Przedstawimy teraz uproszczony schemat konstrukcji modelu ekonometrycznego. Możemy wyróżnić trzy operacje: Zbieramy dane historyczne (empiryczne) xt, yt.

Konstruujemy model yt=f⁢t,xt+ξt, gdzie ξt - błąd przybliżenia.

Konstruujemy model stochastyczny Yt=f⁢t,Xt+εt, gdzie Xt i Yt to zmienne losowe, których realizacją są nasze obserwacje xt i yt, a εt to składnik losowy (też zmienne losowe).

Zakładamy, że w przyszłości Xt i Yt będą związane tą samą zależnością jak dotychczas.

Proszę zwrócić uwagę, że dwie pierwsze operacje aproksymację i estymację możemy wykonać dowolnie dokładnie. Natomiast o ekstrapolacji zawsze ”matematyk teoretyk” będzie mógł powiedzieć, że to ”wróżenie z fusów”.

1. Model konsumpcji
Przez Yt oznaczamy całkowity popyt konsumpcyjny w miesiącu t, a przez Xt dochody gospodarstw domowych w tym okresie. Przyjmujemy, że

gdzie α0 wydatki stałe, α1 część dochodów przeznaczona na konsumpcję, a εt składnik losowy.
Zauważmy, że składnik losowy ”zawiera w sobie” wszystkie czynniki nie uwzględnione w sposób jawny w modelu.

Uwagi:
W modelu zakładamy, że α0 i α1 są stałe, a w rzeczywistości są one tylko wolno-zmienne. Istotną wadą powyższego modelu jest nieuwzględnienie oszczędności.

2. Model oszczędności
Przez Yt oznaczamy stan oszczędności na koniec miesiąca t, a przez Xt dochody gospodarstw domowych w tym miesiącu. Przyjmujemy, że

gdzie β0 wydatki stałe, β1 część dochodów przeznaczona na oszczędności, β2 część oszczędności przeznaczona na konsumpcję, a εt składnik losowy.

Uwagi:
Zauważmy, że w powyższym modelu opóźniona zmienna objaśniana jest zmienną objaśniająca.

Model 1 i 2 można połączyć i otrzymać model dwurównaniowy.

3. Model konsumpcji z uwzględnieniem oszczędności
Przez Y1,t oznaczamy całkowity popyt konsumpcyjny w miesiącu t, przez Y2,t oznaczamy stan oszczędności, a przez Xt dochody gospodarstw domowych w tym okresie. Przyjmujemy, że

gdzie

Uwagi:
Na powyższym przykładzie widzimy, jak z prostszych modeli można konstruować bardziej skomplikowane.
Pytanie: Czy w ten sposób uzyskujemy lepszy opis badanego zjawiska?
Okazuje się, że nie zawsze. Wyznaczanie wartości parametrów dla bardziej złożonego modelu, jest zwykle bardziej skomplikowane i mniej dokładne. W efekcie złożony model, który jest teoretycznie lepszy, w praktyce już takim być nie musi.

4. Model popytu dla dóbr konsumpcyjnych
Przez Yt oznaczamy popyt dla wybranego dobra konsumpcyjnego, przez X1,t jego cenę, a przez X2,t dochody nabywcy. Przyjmujemy, że

Uwagi:
Jest to przykład modelu nieliniowego, który można zlinearyzować za pomocą logarytmowania.

5. Model stochastyczny kursu walutowego
Niech Yt oznacza kurs 1 USD w EUR w dniu t. Przyjmujemy

Po zlogarytmowaniu otrzymujemy model błądzenia przypadkowego

6. Model wydajności pracy
Niech Yt oznacza wydajność pracy w PLN na 1 pracownika, a Xt techniczne uzbrojenie miejsca pracy też w PLN na 1 pracownika. Przyjmujemy

Po zlogarytmowaniu otrzymujemy

Uwagi:
Współczynnik δ mierzy skalę postępu techniczno-organizacyjnego.

1. Klasyfikacja ze względu na dynamikę:
a. Modele statyczne (jednokresowe) charakteryzujące się brakiem zależności od czasu, tzn. F nie zależy od czasu i wśród zmiennych objaśniających nie ma opóźnionych zmiennych objaśnianych. Przykłady 1 i 4.
b. Modele dynamiczne – zależne od czasu lub od opóźnionych zmiennych objaśnianych. Przykłady 2, 3, 5 i 6.
W klasie modeli dynamicznych wyróżniamy modele autoregresyjne w których zależność od czasu wiąże się tylko z występowaniem zmiennych opóźnionych. Przykłady 2, 3 i 5.

2. Klasyfikacja ze względu na postać analityczną modelu:
a. Modele liniowe, postać analityczna jest zadana przez funkcję liniową. Przykłady 1, 2 i 3.
b. Modele nieliniowe, postać analityczna nie jest zadana przez funkcję liniową.
W klasie modeli nieliniowych wyróżniamy modele multiplikatywne, które można zlinearyzować poprzez zlogarytmowanie. Przykłady 4, 5 i 6.

2. Klasyfikacja ze względu na wymiar zmiennej objaśnianej:
a. Modele jednorównaniowe. Przykłady 1, 2, 4, 5 i 6.
b. Modele wielorównaniowe. Przykład 3.

Klasyfikacja ze względu na dynamikę wiąże się z planowanym wykorzystaniem modelu. Do prognozowania potrzebne są modele dynamiczne. Natomiast do badania wpływu zmian konkretnych czynników wystarczy model statyczny.

Klasyfikacja ze względu na postać analityczną modelu i wymiar określa złożoność kalibracji modelu. Jeśli model jest liniowy i jednorównaniowy to istnieją ogólne, w miarę proste, algorytmy (które omówimy na dalszych wykładach) pozwalające sprawnie wyestymować parametry modelu. W przeciwnym wypadku algorytm zależy od konkretnego przypadku i zwykle jest dużo bardziej skomplikowany.