Zagadnienia
2. Podstawowe algorytmy grafiki rastrowej
2.1. Rysowanie odcinka
Współrzędne punktów końcowych odcinka są liczbami całkowitymi;
zakładamy, że
$\Delta x$ = $x_2-x_1$; $\Delta y$ = $y_2-y_1$;
$m$ = $\Delta y/\Delta x$;
for ( $x$ = $x_1$, $y$ = $y_1$; $x$ <= $x_2$; $x$++ ) {
SetPixel ( $x$, round($y$) );
$y$ += $m$;
}
Zmienne float; występuje konieczność
zaokrąglania współrzędnych, a ponadto błędy zaokrągleń
w dodawaniu
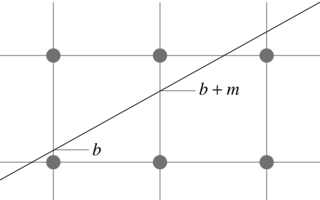
$b$ = $0$;
$\Delta x$ = $x_2-x_1$; $\Delta y$ = $y_2-y_1$;
$m$ = $\Delta y/\Delta x$;
for ( $x$ = $x_1$, $y$ = $y_1$; $x$ <= $x_2$; $x$++ ) {
SetPixel ( $x$, $y$ );
$b$ += $m$;
if ( $b > 1/2$ ) { $y$++; $b$ -= $1$; }
}
W algorytmie II nadal używamy zmiennych real,
ale przyjmują one zawsze wartości wymierne, które można sprowadzić
do wspólnego mianownika
$\Delta x$ = $x_2-x_1$; $\Delta y$ = $y_2-y_1$;
$c$ = $-\Delta x$;
for ( $x$ = $x_1$, $y$ = $y_1$; $x$<=$x_2$; $x$++ ) {
SetPixel ( $x$, $y$ );
$c$ += $2\Delta y$;
if ( $c$ > $0$ ) { $y$++; $c$ -= $2\Delta x$; }
}
Powyższy algorytm rysowania odcinka nazywa się algorytmem Bresenhama. Obecnie jest on powszechnie implementowany w sprzęcie, tj. procesory stosowane w sterownikach (,,kartach”) graficznych zawierają odpowiednie podukłady, które obliczają kolejne piksele rysowanych odcinków właśnie w ten sposób. Mimo to nieraz zdarza się potrzeba użycia odpowiedniego podprogramu, jeśli zadanie nie polega po prostu na wyświetleniu pikseli.
Aby narysować odcinek, którego końce nie spełniają warunków
określonych na początku, trzeba odpowiednio zamienić współrzędne
void DrawLine ( int x1, int y1, int x2, int y2 )
{
int deltax, deltay, g, h, c;
deltax = x2-x1;
if ( deltax > 0 ) g = +1; else g = -1;
deltax = abs(deltax);
deltay = y2-y1;
if ( deltay > 0 ) h = +1; else h = -1;
deltay = abs(deltay);
if ( deltax > deltay ) {
c = -deltax;
while ( x1 != x2 ) {
SetPixel ( x1, y1 );
c += 2*deltay;
if ( c > 0 ) { y1 += h; c -= 2*deltax; }
x1 += g;
}
}
else {
c = -deltay;
while ( y1 != y2 ) {
SetPixel ( x1, y1 );
c += 2*deltax;
if ( c > 0 ) { x1 += g; c -= 2*deltay; }
y1 += h;
}
}
} /*DrawLine*/
Zaletą tej procedury jest fakt, że odcinek zawsze jest rysowany od
pierwszego podanego końca (którego współrzędne są początkowymi
wartościami zmiennych SetPixel ( x2, y2 ), ale jest to zbędne
(a nawet niepożądane) jeśli procedura rysująca odcinek jest używana do
narysowania łamanej.
Przyjrzyjmy się jeszcze zawartości poszczególnych wierszy, narysowanej
przez algorytm III: w wierszu SetHLine ( $x_1$, $x_2$, $y$ );,
która rysuje
if ( $y_2=y_1$ ) SetHLine ( $x_1$, $x_2+1$, $y_1$ );
else {
$\Delta x$ = $x_2-x_1$; $\Delta y$ = $y_2-y_1$;
$m$ = $\Delta x$ / $\Delta y$; $\Delta\tilde{x}$ = $\Delta x-m$*$\Delta y$;
$c$ = $-\Delta y$;
$x_3$ = $x_1-m$ / $2$; $x_4$ = $x_3+m$;
SetHLine ( $x_1$, $x_4$, $y_1$ );
for ( $y$ = $y_1+1$; $y<y_2$ ) {
$c$ = $c+2\Delta\tilde{x}$;
$x_3$ = $x_4$;
if ( $c>0$ ) { $x_4$ = $x_4+m+1$; $c$ := $c-2\Delta y$; }
else $x_4$ = $x_4+m$;
SetHLine ( $x_3$, $x_4$, $y$ );
}
SetHLine ( $x_3$, $x_2$, $y_2$ );
}
Oprócz zmniejszenia liczby obliczeń błędów dla odcinków nachylonych
pod małymi kątami, do szybkości działania tej procedury przyczynia się
fakt, że przypisanie koloru wielu pikselom położonym obok siebie
w poziomej linii rastra (przez procedurę SetHLine) może zająć
znacznie mniej czasu niż przypisywanie koloru tym pikselom po kolei, m.in. dzięki uproszczeniu obliczania adresów (w pamięci obrazu) sąsiednich
pikseli.
2.2. Rysowanie okręgu
Rysując okrąg warto wykorzystać ośmiokrotną symetrię jego obrazu
rastrowego; jeśli ma on środek Set8Pixels, która może też
dodać do ich współrzędnych współrzędne środka okręgu.
Wystarczy więc wyznaczyć piksele, które tworzą obraz jednej ósmej
okręgu. Zasada działania algorytmu Bresenhama rysowania okręgu jest
ta sama co w przypadku odcinka: wybieramy kolejne piksele starając się
zminimalizować błąd, tj. odległość piksela od przedstawianej na
obrazie figury.
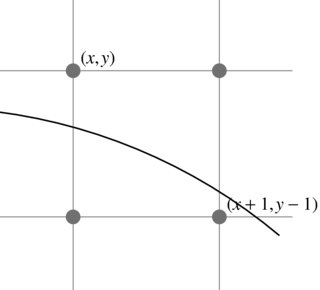
Aby wyprowadzić algorytm rysowania okręgu, rozważmy dwie tożsamości:
Wynika z nich, że funkcja
ma wartość
Uwaga: To nie zapewnia wyboru piksela bliżej okręgu, tylko
piksela, dla którego funkcja
Mamy
$x$ = $0$;
$y$ = $r$;
$c$ = $2(1-r)$;
while ( $x\leq y$ ) {
Set8Pixels ( $x$, $y$ );
if ( $2c > 1-2y$ ) { /* czasem w dół */
$y$ --;
$c$ -= $2y-1$;
}
$x$++; /* zawsze w bok */
$c$ += $2x+1$;
}
2.3. Rysowanie elips
Jeśli współczynnik aspekt rastra, czyli iloraz szerokości
i wysokości piksela (tj. odległości środka piksela od środków pikseli
sąsiednich z boku i z góry) jest różny od Set8Pixels zmienioną
w ten sposób, aby zamiast SetPixel ( $x$, $y$ );
wywoływała SetPixel ( $(x$*$a)$/$b$, $y$ );
(tu jest założenie, że
Metoda druga, sporo trudniejsza, polega na narysowaniu okręgu o promieniu
Opisane wyżej metody mają na celu rysowanie elips, których jedna oś jest pozioma, a druga pionowa. Jeśli elipsa, którą trzeba narysować nie spełnia tego warunku (tj. jest w położeniu ogólnym), to można zastosować metodę odpowiednią dla dowolnej krzywej ciągłej: wyznaczyć dostatecznie dużo punktów i narysować łamaną.
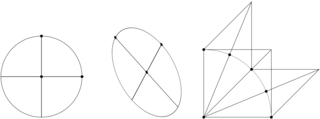
Aby narysować elipsę (lub dowolny inny obiekt), należy mieć jej odpowiednią reprezentację. Wygodne jest użycie średnic sprzężonych. Jak wiadomo, elipsa jest obrazem okręgu w pewnym przekształceniu afinicznym. Średnice sprzężone elipsy są obrazem pary prostopadłych średnic tego okręgu w tym samym przekształceniu afinicznym. Mając taką reprezentację możemy zastosować strategię ,,dziel i zdobywaj”. Mając dwa punkty końcowe łuku elipsy możemy zbadać, czy leżą one dostatecznie blisko. Jeśli tak, to narysujemy odcinek. Jeśli nie, to wyznaczymy punkt ,,środkowy” tego łuku, a następnie dwa łuki otrzymane z podziału łuku danego w wyznaczonym punkcie narysujemy stosując tę procedurę rekurencyjnie.
Rozważmy łuk okręgu jednostkowego o środku
void r_Elipsa ( $k$, $\bm{c}$, $\bm{v}_1$, $\bm{v}_2$ )
{
if ( dostatecznie blisko ( $\bm{v}_1$, $\bm{v}_2$ ) )
rysuj_odcinek ( $\bm{c}+\bm{v}_1$, $\bm{c}+\bm{v}_2$ );
else {
$\bm{v}_3$ = $a_k$*$(\bm{v}_1+\bm{v}_2)$;
r_Elipsa ( $k+1$, $\bm{c}$, $\bm{v}_1$, $\bm{v}_3$ );
r_Elipsa ( $k+1$, $\bm{c}$, $\bm{v}_3$, $\bm{v}_2$ );
}
} /*r_Elipsa*/
Parametry wywołania procedury przez program główny to
Współczynniki
2.4. Wypełnianie wielokątów
Dany jest
W dobrze zaprojektowanych pakietach graficznych jest przyjęta i konsekwentnie przestrzegana umowa dotycząca rozstrzygania, czy piksel, którego środek leży na brzegu wielokąta, należy do niego, czy nie. Na przykład:
-
Jeśli środek piksela leży na krawędzi aktywnej, to piksel jest zamalowywany wtedy, gdy wnętrze wielokąta jest z prawej strony krawędzi;
-
Piksele leżące na krawędzi poziomej są zamalowywane wtedy gdy wnętrze wielokąta leży poniżej tej krawędzi.
Dzięki takiej umowie, jeśli mamy wielokąty o wspólnych krawędziach, to
każdy piksel na takiej krawędzi należy do dokładnie jednego wielokąta.
Ma to szczególne znaczenie w rysowaniu z przypisywaniem pikselom wartości
zależnej od wartości poprzedniej (np. w trybie xor itd.).
Do wykonania zadania posłuży nam następująca reguła parzystości: punkt leży wewnątrz wielokąta, jeśli dowolna półprosta, która z niego wychodzi przecina brzeg wielokąta nieparzystą liczbę razy.
Algorytm przeglądania liniami poziomymi składa się z następujących kroków:
Utwórz tablicę krawędzi (par kolejnych wierzchołków, w tym $(x_n,y_n)$,$(x_1,y_1)$);
Dla każdej krawędzi, jeśli współrzędna $y$ jej drugiego końca jest mniejsza,
zamień końce; krawędzie poziome usuń z tablicy;
Posortuj tablicę w kolejności rosnących współrzędnych $y$ pierwszego końca;
Utwórz początkowo pustą tablicę krawędzi aktywnych (t.k.a.), czyli przeciętych kolejną linią poziomą;
$y$ = współrzędna $y$ pierwszej krawędzi w tablicy;
do {
Wstaw $\mbox{do}$ t.k.a. krawędzie, których pierwszy koniec jest na linii $y$;
Oblicz dla każdej krawędzi w t.k.a. współrzędną $x$ punktu przecięcia z linią poziomą $y$;
Posortuj t.k.a. w kolejności rosnących współrzędnych $x$ punktów przecięcia;
Dla kolejnych par krawędzi aktywnych rysuj odcinek poziomy na linii $y$,
między ich punktami przecięcia z linią $y$;
$y$ ++;
Usuń z t.k.a. krawędzie, których drugi koniec jest na linii $y$;
} while ( t.k.a jest niepusta );
Uwaga: Tablica krawędzi aktywnych po każdym uaktualnieniu zawiera parzystą liczbę elementów.
2.5. Wypełnianie obszaru przez zalewanie
Przypuśćmy, że należy zamalować obszar, którego brzeg został narysowany wcześniej i obszar jest określony przez dany na początku obraz. Mamy tu więc problem z pogranicza grafiki i przetwarzania obrazów. Aby rozwiązać takie zadanie, należy je nieco uściślić, przez wprowadzenie dodatkowych pojęć.
Figura rastrowa jest czterospójna, jeśli za sąsiadów dowolnego
piksela uznajemy cztery inne piksele (dwa po bokach i po jednym powyżej
i poniżej; innymi słowy, sąsiadami piksela
Figura jest ośmiospójna, jeśli za sąsiadów piksela uznajemy
oprócz podanych wyżej jeszcze cztery piksele, które mają wspólny
narożnik z pikselem danym i dla dowolnych dwóch pikseli należących do tej
figury istnieje droga złożona z
Reguły spójności odgrywają dużą rolę w rozpoznawaniu obrazów, które polega na identyfikowaniu linii i innych figur na obrazie; tymczasem zauważmy następującą regułę: brzeg obszaru ośmiospójnego jest czterospójny; brzeg obszaru czterospójnego jest ośmiospójny.
Mając określone sąsiedztwo pikseli w rastrze, dowolną figurę możemy reprezentować za pomocą grafu sąsiedztwa pikseli; jego wierzchołkami są piksele należące do figury; jego krawędziami są wszystkie krawędzie łączące wierzchołki, które są sąsiednie (w sensie jednej z powyższych definicji).
Algorytm wypełniania przez zalewanie (ang. flood fill) polega na przeszukaniu grafu sąsiedztwa pikseli obszaru, którego reprezentacją jest początkowy obraz rastrowy. Oprócz obrazu należy podać tzw. ziarno, czyli jeden piksel, który należy do obszaru, ale nie do jego brzegu. W wielu książkach jest podana procedura rekurencyjna, która stosuje metodę przeszukiwania grafu w głąb (ang. depth-first search, DFS); w wersji dla obszaru czterospójnego wygląda ona następująco:
void r_FloodFill ( $x$, $y$ )
{
if ( niezamalowany ( $x$, $y$ ) ) {
SetPixel ( $x$, $y$ );
r_FloodFill ( $x+1$, $y$ );
r_FloodFill ( $x-1$, $y$ );
r_FloodFill ( $x$, $y+1$ );
r_FloodFill ( $x$, $y-1$ );
}
} /*r_FloodFill*/
Wadą przeszukiwania w głąb jest ogromne zapotrzebowanie na pamięć
(w tym przypadku stos rekurencyjnych wywołań procedury). Trzeba się liczyć
z koniecznością przechowania na nim rekordów aktywacji procedury dla
wszystkich pikseli w obszarze (czyli np. rzędu
Znacznie lepiej działa przeszukiwanie wszerz (ang. breadth-first search, BFS), które polega na użyciu kolejki. Ziarno wstawiamy do pustej kolejki, a następnie, dopóki kolejka nie jest pusta, wyjmujemy z niej piksel, i jeśli jest niezamalowany, to zamalowujemy go i wstawiamy jego sąsiadów do kolejki. Potrzebna pojemność kolejki jest rzędu liczby pikseli na brzegu obszaru.
Jeszcze sprawniejsza procedura wyznacza graf sąsiedztwa linii; jego wierzchołkami są poziome odcinki (o maksymalnej długości), złożone z pikseli należących do obszaru. Na razie tego tematu nie rozwijam.
2.6. Algorytm z pływającym horyzontem
Jednym z efektownych i użytecznych zastosowań algorytmu Bresenhama jest
rysowanie wykresów funkcji dwóch zmiennych, tj. obrazów powierzchni
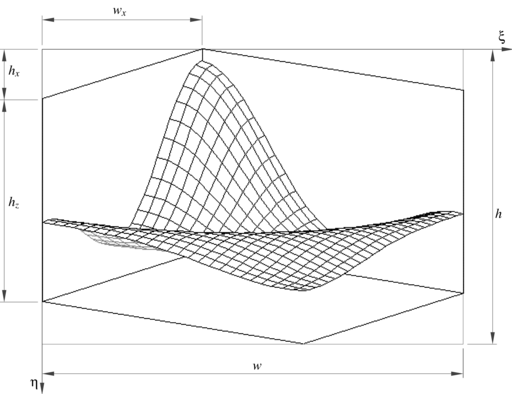
Algorytm rysuje wykres funkcji w danym prostokącie
Wykres funkcji mieści się więc w kostce
Współczynniki
Istotne w określeniu tego przekształcenia dla algorytmu z pływającym
horyzontem jest to, że obrazy punktów, które mają identyczne
współrzędne
Rysowanie wykresu następuje ,,od przodu do tyłu”, przy czym wcześniej
narysowane odcinki ograniczają obszar ,,zasłonięty”, w którym nie wolno
rysować. W każdej kolumnie pikseli obszar ten jest odcinkiem, którego
końcami są najwyższy i najniższy piksel narysowany wcześniej w tej
kolumnie. Dla każdej kolumny pikseli potrzebujemy zatem dwóch zmiennych
całkowitych do zapamiętania współrzędych
Aby wykonać wykres obliczamy wartości funkcji
Rozwiązaniem tego problemu jest dwukrotne wywołanie algorytmu Bresenhama
dla każdego odcinka, z różnymi procedurami wywoływanymi w celu przetworzenia
pikseli. Za pierwszym razem wykonujemy test widoczności i rysowanie, a za
drugim razem uaktualniamy horyzonty. Procedura DrawLine,
realizująca algorytm Bresenhama, otrzymuje procedurę przetwarzającą
piksele jako parametr, zatem jej nagłówek musi być taki:
void DrawLine ( int x1, int y1, int x2, int y2, void (*SetPixel)(int x, int y) );
Jako ostatni parametr będziemy przekazywać dwie różne procedury.
Procedura SetPixel1 sprawdza widoczność i rysuje (wywołując ,,prawdziwą” procedurę
rysowania piksela), zaś SetPixel2 uaktualnia horyzonty.
Zmienne wdt i hgh opisują wymiary obrazu (w pikselach).
W tablicy ftab
są przechowywane końce odcinków do narysowania (w tym kodzie jest to
tablica jednowymiarowa, o długości (densx+1)*(densy+1), gdzie
parametry densx i densy określają gęstość siatki).
Tablice fhup i fhdn opisują horyzont górny i dolny
(rezerwowanie i zwalnianie pamięci na te tablice zostało
pominięte). Procedury SetPixel1 i SetPixel2 są dodatkowo
wywoływane poza procedurą DrawLine po to, aby uzupełnić brak
ich wywołania dla ostatniego piksela rysowanych odcinków
(w całym obrazie trzeba w ten sposób uzupełnić tylko jeden piksel).
Podany niżej fragment programu w C rysuje odcinki parami.
short *fhup, *fhdn;
void SetPixel1 ( int x, int y )
{
if ( y <= fhdn[x] && y >= fhup[x] )
return;
SetPixel ( x, y );
} /*SetPixel1*/
void SetPixel2 ( int x, int y )
{
if ( y > fhdn[x] ) fhdn[x] = y;
if ( y < fhup[x] ) fhup[x] = y;
} /*SetPixel2*/
...
for ( i = 0; i < wdt; i++ )
{ fhup[i] = hgh; fhdn[i] = -1; }
for ( j = k = 0; j < densy; j++, k++ ) {
pa = ftab[k]; pb = ftab[k+1];
DrawLine ( pa.x, pa.y, pb.x, pb.y, &SetPixel1 );
DrawLine ( pa.x, pa.y, pb.x, pb.y, &SetPixel2 );
}
SetPixel1 ( pb.x, pb.y ); SetPixel2 ( pb.x, pb.y );
for ( i = 1, k = densy+1; i <= densx; i++, k++ ) {
pa = ftab[k]; pb = ftab[k-densy-1];
DrawLine ( pa.x, pa.y, pb.x, pb.y, &SetPixel1 );
DrawLine ( pa.x, pa.y, pb.x, pb.y, &SetPixel2 );
for ( j = 0; j < densy; j++, k++ ) {
pb = pa; pa = ftab[k+1]; pc = ftab[k-densy];
DrawLine ( pb.x, pb.y, pa.x, pa.y, &SetPixel1 );
DrawLine ( pa.x, pa.y, pc.x, pc.y, &SetPixel1 );
DrawLine ( pb.x, pb.y, pa.x, pa.y, &SetPixel2 );
DrawLine ( pa.x, pa.y, pc.x, pc.y, &SetPixel2 );
}
}
...
Pozostaje mi zaproponować uzupełnienie tego kodu do pełnego programu,
uruchomienie, eksperymenty i dorabianie bajerów, takich jak obliczanie
kolorów pikseli zależnie od wartości funkcji