Dane są punkty końcowe odcinka, p1=x1,y1 i p2=x2,y2, oraz współczynniki a, b, c równania prostej a⁢x+b⁢y=c. Mamy znaleźć (jeśli istnieje) punkt wspólny tego odcinka i prostej.

Przedstawienie parametryczne odcinka, p=p1+t⁢p2-p1, czyli

wstawiamy do równania prostej, otrzymując równanie

którego rozwiązaniem jest

Jeśli t∉0,1, to prosta i odcinek są rozłączne. W przeciwnym razie możemy obliczyć współrzędne x, y punktu wspólnego. Wzór jest szczególnie prosty w przypadku, gdy równanie prostej obcinającej ma postać x=c (prosta jest wtedy pionowa), lub y=c (prosta jest pozioma).

Prawie identyczne jest wyprowadzenie odpowiednich wzorów w przestrzeni trójwymiarowej, dla danych punktów końcowych x1,y1,z1, x2,y2,z2 i równania płaszczyzny obcinającej a⁢x+b⁢y+c⁢z=d.

Omówimy najbardziej popularną wersję obcinania do okna prostokątnego. Dla dowolnego wielokąta/wielościanu wypukłego zasada działania algorytmu jest identyczna.

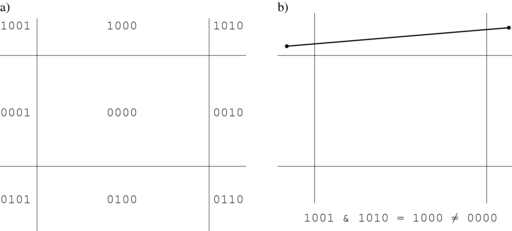
Dane są punkty końcowe odcinka i prostokątne okno. Proste, na których leżą krawędzie okna, dzielą płaszczyznę na 9 obszarów. Przyporządkujemy im czterobitowe kody przedstawione na rysunku 3.1a.

Kody obszarów, do których należą końce odcinka, możemy wyznaczyć na podstawie ich współrzędnych. Zauważmy, że jeśli oba kody na dowolnej pozycji mają jedynkę, to cały odcinek leży poza oknem (rys. 3.1b). Jeśli oba punkty końcowe mają kod 0, to cały odcinek leży wewnątrz okna. Jeśli kody są różne od 0, ale nie mają jedynki jednocześnie na żadnej pozycji, to odcinek może, ale nie musi mieć części wewnątrz okna.

Dla dowolnego wielokąta lub wielościanu określa się kody o liczbie bitów równej liczbie krawędzi albo ścian. Algorytm wyznacza punkt przecięcia odcinka z krawędzią, której odpowiada 1 w którymś kodzie, a następnie zastępuje jeden z punktów (ten, w którego kodzie występuje ta jedynka) przez punkt przecięcia. Nie grozi przy tym dzielenie przez 0 (dlaczego?).

Wadą algorytmu Sutherlanda-Cohena jest to, że obliczane są punkty, które mogą być następnie odrzucone (ponieważ leżą poza oknem). Zabiera to czas, a ponadto wprowadza większe błędy zaokrągleń. Aby otrzymać algorytm pozbawiony tych wad, skorzystamy z parametrycznego przedstawienia odcinka (3.1). Oznaczymy Δ⁢x=x2-x1, Δ⁢y=y2-y1. Aby dokonać obcięcia odcinka, zawęzimy przedział zmienności parametru t do przedziału odpowiadającego części wspólnej odcinka z oknem, a dopiero potem wyznaczymy punkty końcowe. Zauważmy, że w ogólności możemy przyjąć na początku inny przedział niż 0,1, co umożliwi obcinanie odcinka który leży na prostej przechodzącej przez punkty x1,y1 i x2,y2, ale o innych końcach. Możemy nawet przyjąć początkowy przedział -∞,+∞, który reprezentuje całą prostą (ale wtedy procedura obcinania musi wyprowadzić wynik w postaci odpowiednich wartości parametru prostej).

Wartością funkcji jest 1 jeśli przynajmniej część odcinka jest widoczna i 0 w przeciwnym razie. Zasada działania algorytmu wiąże się z interpretacją prostych, na których leżą krawędzie okna, jako zbiorów algebraicznych. Funkcja f⁢x,y=a⁢x+b⁢y-c, której zbiorem miejsc zerowych jest taka prosta, jest dodatnia w półpłaszczyźnie zawierającej okno (to jest zapewnione przez odpowiedni wybór znaku współczynników a, b, c). Parametr q funkcji Test otrzymuje wartość tej funkcji w punkcie p1 kolejno dla każdej krawędzi okna. Po wykryciu, że przedział zmienności parametru t jest pusty, funkcja ma wartość 0. W przeciwnym razie, po obcięciu wszystkimi krawędziami okna, procedura oblicza punkty końcowe części odcinka widocznej w oknie (uwaga na kolejność obliczania tych punktów; w pewnej książce wykryłem błąd, polegający na zmianie kolejności).

Algorytm Lianga-Barsky'ego, podobnie jak algorytm Sutherlanda-Cohena, może być łatwo zmodyfikowaniy w celu obcinania odcinków do dowolnych wielokątów lub wielościanów wypukłych.

Jeśli mamy wyznaczyć część wspólną danej prostej i prostokątnego okna, to możemy użyć algorytmu Lianga-Barsky'ego. Opierając się na przedstawieniu prostej w postaci niejawnej, za pomocą równania liniowego a⁢x+b⁢y=c, możemy to zadanie wykonać jeszcze trochę szybciej. W tym celu trzeba obliczyć wartości funkcji f⁢x,y=a⁢x+b⁢y-c w wierzchołkach okna, a następnie, badając znaki wartości funkcji f w tych punktach, wyznaczyć punkty przecięcia prostej tylko z tymi krawędziami okna, które są przez prostą przecięte. Zysk z takiego podejścia to kilka zaoszczędzonych działań arytmetycznych, co (w przypadku średnim) przekłada się na prawie o połowę krótszy czas działania. Ponieważ procedury obcinania należą do oprogramowania podstawowego w bibliotekach graficznych (często są one implementowane sprzętowo) i wywoływane wiele razy, więc każde ich przyspieszenie jest istotne.

Zajmiemy się wyznaczaniem części wspólnej wielokąta i półpłaszczyzny. Wyznaczanie przecięcia dwóch wielokątów, z których przynajmniej jeden jest wypukły (np. jest prostokątnym oknem) można wykonać za pomocą kilkakrotnego obcinania do półpłaszczyzny.

Założymy, że brzeg wielokąta jest jedną łamaną zamkniętą. Jeśli tak nie jest (wielokąt ma dziury i łamanych jest więcej), to każdą łamaną trzeba obciąć osobno. Brzeg wielokąta obciętego przez opisany niżej algorytm Sutherlanda-Hodgmana też jest łamaną zamkniętą, zorientowaną zgodnie z brzegiem wielokąta danego.

W algorytmie Sutherlanda-Hodgmana kolejno przetwarzamy boki wielokąta (odcinki łamanej zamkniętej). Zmienna s reprezentuje punkt końcowy poprzedniego odcinka. Wywoływana przez poniższą procedurę funkcja Inside ma wartość true jeśli punkt podany jako argument leży we ,,właściwej” półpłaszczyźnie. Funkcja Intersect oblicza punkt przecięcia odcinka (o końcach podanych jako parametry). Procedura Output ma za zadanie wyprowadzić kolejny wierzchołek obciętego wielokąta, co może polegać na wstawieniu go do tablicy.

Zauważmy, że jeśli wielokąt nie jest wypukły, to jego część wspólna z półpłaszczyzną (albo oknem) może nie być spójna. Dostajemy wtedy na wyjściu łamaną, której krawędzie mają wspólne części (i części te są przeciwnie zorientowane). Jeśli po obcięciu wypełniamy wielokąt algorytmem przeglądania liniami poziomymi, to obecność tych ,,fałszywych krawędzi” nie ma znaczenia, choć jeśli brzeg półpłaszczyzny jest ukośny (tj. nie jest prostą pionową ani poziomą), to po zaokrągleniu współrzędnych wierzchołków do liczb całkowitych błędy mogą się ukazać (w postaci błędnie zamalowanych pikseli).

W różnych zastosowaniach zdarza się potrzeba wyznaczenia części wspólnej, sumy lub różnicy dwóch wielokątów dowolnych, tj. niekoniecznie wypukłych. Umożliwia to algorytm Weilera-Athertona, który dopuszcza jako dane wielokąty, których brzegi mogą składać się z wielu zamkniętych łamanych; wielokąty takie mogą być niejednospójne, tj. z dziurami, albo nawet niespójne.

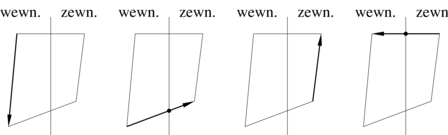
Podstawowe wymaganie, konieczne aby wynik był dobrze określony, to właściwe zorientowanie brzegu. Dla ustalenia uwagi przyjmiemy umowę, że każda krawędź jest zorientowana w ten sposób, że poruszając się wzdłuż niej zgodnie z orientacją mamy wnętrze wielokąta po prawej stronie (rys. 3.4). Aby wyznaczyć przecięcie wielokątów, kolejno

1. Konstruujemy reprezentacje dwóch grafów zorientowanych; wierzchołkami i krawędziami każdego z nich są wierzchołki i zorientowane krawędzie jednego z wielokątów.

2. Znajdujemy wszystkie punkty przecięcia krawędzi jednego wielokąta z krawędziami drugiego. Dzielimy krawędzie, na których leżą te punkty, na kawałki; dołączamy w ten sposób nowe wierzchołki do grafu, zachowując uporządkowanie punktów podziału krawędzi w grafie. Wprowadzamy dodatkowe powiązanie między wierzchołkami grafów, które odpowiadają temu samemu punktowi (przecięcia). Tworzy się w ten sposób jeden graf, którego krawędzie reprezentują kawałki brzegu jednego lub drugiego wielokąta.

3. Znajdujemy wierzchołek grafu, który jest wierzchołkiem przecięcia wielokątów. Może to być wierzchołek odpowiadający punktowi przecięcia brzegów wielokątów, a jeśli takiego nie ma, to możemy sprawdzić, czy jakiś wierzchołek leży wewnątrz drugiego wielokąta, korzystając z reguły parzystości. Wybieramy wychodzącą ze znalezionego wierzchołka krawędź, która jest krawędzią przecięcia (wyboru dokonujemy na podstawie orientacji brzegów).

   Zaczynając od znalezionego wierzchołka, obchodzimy graf, aż do trafienia ponownie na wierzchołek, z którego wyszliśmy. W każdym wierzchołku, który odpowiada przecięciu brzegów, wybieramy krawędź wielokąta innego niż ten, po którego krawędzi poruszaliśmy się. Odwiedzone wierzchołki wyprowadzamy; ich ciąg reprezentuje odpowiednio zorientowany fragment (zamkniętą łamaną) przecięcia wielokątów danych.

   Algorytm kończy działanie po stwierdzeniu braku nieodwiedzonego wierzchołka należącego do brzegu wielokątów.

Mając algorytm, który wyznacza przecięcie wielokątów, łatwo możemy otrzymać algorytm wyznaczania sumy lub różnicy; dany brzeg określa wielokąt, ale także jego dopełnienie — wystarczy tylko odwrócić orientację wszystkich krawędzi. W ten sposób sumę wielokątów otrzymamy jako dopełnienie przecięcia ich dopełnień.

Ważne dla poprawnej implementacji algorytmu jest uwzględnienie przypadków, gdy wielokąty mają wspólne wierzchołki lub gdy ich krawędzie mają wspólne odcinki. Pewne punkty mogą też być końcami więcej niż dwóch krawędzi wielokąta. Istotna jest możliwość wykonywania działań na wielokątach otrzymanych za pomocą tego algorytmu, i wtedy takie sytuacje zdarzają się często.