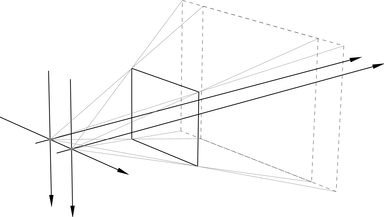Zagadnienia
5. Rzutowanie równoległe, perspektywiczne i inne
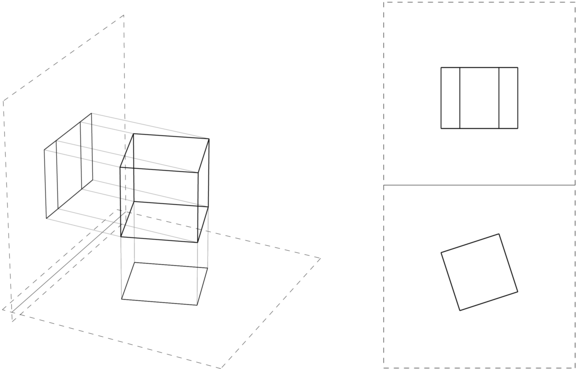
5.1. Rzutowanie równoległe
Obrazem dowolnego punktu
Takie rzutowanie równoległe jest powszechnie używane w rysunku technicznym, gdzie jednym z celów jest umożliwienie odtworzenia (restytucji) punktu w przestrzeni na podstawie rysunku. Inna potrzeba, do pewnego czasu dominująca w projektowaniu przemysłowym, to dokonywanie konstrukcji geometrycznych w przestrzeni trójwymiarowej na płaskich rysunkach. Na podstawie tych potrzeb rozwinęła się geometria wykreślna, która obecnie wydaje się być sztuką w zaniku — użycie komputerów zwalnia od wysiłków i coraz częściej przedmiot ten jest wykładany już tylko po to, aby rozwijać wyobraźnię przestrzenną u studentów architektury (tego, niestety, czy na szczęście, komputer nie zastąpi). Istnieją dwa podstawowe podejścia do stosowania rzutowania równoległego w rysunku technicznym: metoda Monge'a6Gaspard Monge, 1746–1818, czyli wykonywanie konstrukcji trójwymiarowych na dwóch obrazach będących rzutami prostopadłymi na dwie, wzajemnie prostopadłe rzutnie, oraz aksonometria.
Podstawowe znaczenie dla aksonometrii ma twierdzenie Pohlkego: dobierając odpowiednio rzutnię i kierunek rzutowania można odwzorować wierzchołki danego czworościanu na figurę podobną do zbioru dowolnych czterech punktów, z których żadne trzy nie leżą na jednej prostej.
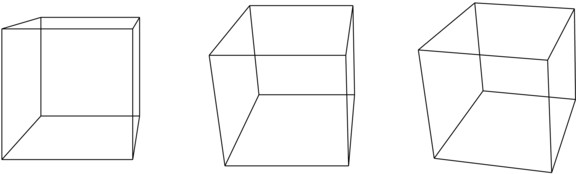
Na podstawie tego twierdzenia możemy określić rzut aksonometryczny, wybierając obraz początku układu współrzędnych i trzy wektory (z których żadne dwa nie są liniowo zależne) — obrazy wersorów osi. W ten sposób postąpiliśmy w celu narysowania wykresu funkcji przy użyciu algorytmu z pływającym horyzontem, określając rzut aksonometryczny. Rzuty stosowane najczęściej w rysunku technicznym są pokazane rysunku 5.3
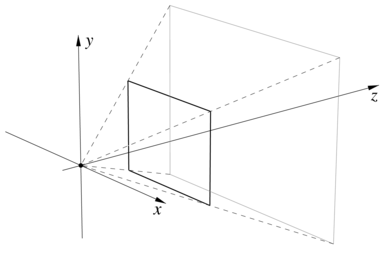
5.2. Rzutowanie perspektywiczne
Obrazem punktu
Rzut równoległy można interpretować jako graniczny przypadek rzutu perspektywicznego, gdy obserwator znajduje się w bardzo dużej odległości.
W rysunkach technicznych części maszyn rzut perspektywiczny bywa używany bardzo rzadko, głównie w rysunkach poglądowych, takich jak schematy montażowe, natomiast często stosuje się go w architekturze. Opracowanie konstrukcji geometrycznych związanych z tym sposobem rzutowania wiąże się z historią malarstwa, którą tu się nie zajmujemy.
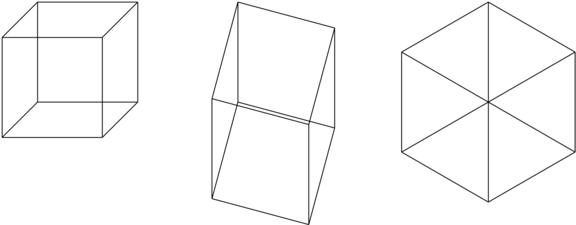
Zależnie od położenia rzutni względem głównego obiektu na obrazie, mówimy o perspektywie jednopunktowej, dwupunktowej i trzypunktowej. Z obiektem związane są trzy kierunki osi, jakoś powiązane z obiektem (najbardziej oczywisty związek jest wtedy, gdy obiekt jest prostopadłościanem). Poszczególne przypadki otrzymamy wybierając rzutnię tak, aby jeden, dwa lub trzy spośród tych kierunków nie były równoległe do rzutni.
5.3. Algorytm rzutowania
Przekształcenie rzutowe jest to przekształcenie przestrzeni
rzutowej (tj. afinicznej uzupełnionej o punkty niewłaściwe, czyli
kierunki), któremu odpowiada różnowartościowe (czyli o nieosobliwej
macierzy) przekształcenie liniowe przestrzeni jednorodnej. Macierz
reprezentująca przekształcenie afiniczne we współrzędnych
jednorodnych ma ostatni wiersz o postaci
Dowolne przekształcenia rzutowe są nieco rzadziej niż afiniczne stosowane w modelowaniu obiektów, ale przydają się do określenia rzutowania perspektywicznego, a zatem ich implementacja jest zawsze potrzebna w grafice ,,trójwymiarowej” i często realizowana w sprzęcie.
Rzutowanie, tj. odwzorowanie przestrzeni trójwymiarowej na płaszczyznę ekranu, zwykle określa się opisując za pomocą odpowiednich parametrów tzw. wirtualną kamerę, przy czym w różnych pakietach graficznych szczegóły tego postępowania mogą być różne. Wirtualna kamera związana jest z kartezjańskim układem współrzędnych kamery i pierwszy krok rzutowania punktu polega na obliczeniu jego współrzędnych w tym układzie.
Przypuśćmy, że początek układu współrzędnych kamery jest
położeniem obserwatora (albo środkiem obiektywu) i że oś
Rzutowanie równoległe polega na zignorowaniu współrzędnej
Wynikiem mnożenia jest wektor
Po obliczeniu wspołrzędnych jednorodnych wykonuje się dwa dzielenia, a następnie dokonuje jeszcze jednego przekształcenia afinicznego, którego celem jest przejście do współrzędnych urządzenia (jednostką w tym układzie jest szerokość lub wysokość piksela). Współrzędne w układzie urządzenia można następnie zaokrąglić i przystąpić do rysowania.
Zatrzymajmy się jeszcze na kroku poprzednim. Współrzędna
Dokonując rzutowania równoległego możemy użyć macierzy jednostkowej;
wtedy otrzymamy wynik
Macierz ta jest nieosobliwa, a iloczynem jej i wektora
Określając rzutowanie w programach korzystajacych z różnych pakietów
oprogramowania, należy podać zakres głębokości, tj. granice
przedziału
na podstawie którego możemy obliczyć
Wiemy już dostatecznie dużo, aby rozszyfrować sposób tworzenia
macierzy rzutowania wykorzystywany przez standard OpenGL.
W standardzie tym bryła widzenia jest poddawana takiemu przekształceniu,
aby jej obraz był kostką glFrustum, ma postać
Symbole
Macierz tworzona przez procedurę glOrtho realizuje rzutowanie równoległe;
bryła widzenia w układzie kamery jest prostopadłościanem, który zostaje
odwzorowany na kostkę
Obcinanie, rozstrzyganie widoczności i dalsze etapy rysowania przebiegają tak samo jak w przypadku rzutowania perspektywicznego.
5.4. Stereoskopia
Wrażenie widzenia przestrzennego, czyli postrzeganie głębi obrazu, powstaje w mózgu obserwatora na podstawie dwóch obrazów na siatkówkach dwojga oczu. W świecie zwierząt jest to dość rzadkie zjawisko; zwróćmy uwagę na własności ludzkiego narządu wzroku, które to umożliwiają:
-
Pola widzenia obojga oczu prawie w całości pokrywają się.
-
Rozstaw oczu jest ustalony, sporo większy od ich wielkości i porównywalny z wielkością oglądanych obiektów (jeśli oglądamy duże obiekty, np. budynki, to wrażenie trójwymiarowości powstaje na podstawie poprzednich doświadczeń i oglądania obiektu z różnych stron; odległości położeń obserwatora są wtedy porównywalne z wielkością budynku).
-
Ludzkie oko ma bardzo dużą głębię ostrości (tj. szeroki zakres odległości, w których jednocześnie jest w stanie ,, widzieć ostro”).
Dzięki powyższemu zbiegowi okoliczności wystarczy zapewnić, aby każde oko widziało odpowiedni obraz, którego odległość od oka jest raczej nieistotna. Techniki oglądania ,,obrazów przestrzennych” są następujące:
-
Użycie kasku z wbudowanymi miniaturowymi monitorami,
-
Zastosowanie okularów z ciekłymi kryształami; prawa i lewa szyba stają się na przemian nieprzezroczyste, a na ekranie są wtedy wyświetlane obrazy lewy i prawy.
Ta technika umożliwia oglądanie obrazów ,,trójwymiarowych” nie tylko na ekranie monitora lub telewizora, ale także na dużych ekranach, które są ścianami pomieszczenia. W takim pomieszczeniu może przebywać nawet duża grupa osób (z których każda ma swoje okulary), które odbierają poprawnie wrażenia widzenia przestrzennego. Potwierdza to fakt, że stosunkowo łatwo jest wywołać takie wrażenia u ludzi, którzy dobrze tolerują zniekształcenia wywołane wyświetlaniem obrazów otrzymanych z innego niż rzeczywiste położenia obserwatora.
-
Można użyć kolorowych okularów, np. z czerwoną i zieloną szybą i wyświetlać każdy obraz w innym kolorze (takie rysunki są znane od dawna pod nazwą anaglify).
-
Istnieją też obrazy ,,magiczne oko”, złożone z pozornie chaotycznych plam, wśród których można dostrzec obiekty trójwymiarowe.
Aby otrzymać odpowiednie dwa obrazy należy określić dwa rzuty
perspektywiczne (po jednym dla każdego oka). Aby to zrobić poprawnie,
trzeba ustalić
odpowiedni układ współrzędnych — prostokątny, o wersorach osi
o identycznej długości, która jest jednostką odległości potrzebną
dalej. Przypuśćmy, że jednostką tą jest
5.5. Panorama i inne rzuty
Istnieje wiele różnych stosowanych w praktyce odwzorowań przestrzeni w płaszczyznę; mogą one być określone przy użyciu rzutowania na powierzchnie krzywoliniowe, które następnie są przekształcane w płaszczyznę. Warto zauważyć, że obrazem odcinka w takim rzucie może być łuk krzywej, co stanowi utrudnienie podczas wykonywania obrazów.
Teoretycznie najprostsze jest przekształcenie w płaszczyznę powierzchni rozwijalnych, ale rzeczywiście łatwe do zrealizowania jest rozwinięcie tylko powierzchni walcowej. Możemy przyjąć jako rzutnię powierzchnię boczną walca (lub jej fragment), wybrać środek rzutowania w dowolnym punkcie jego osi, a następnie odwzorować rzutnię w płaszczyznę. Takie odwzorowanie nazywa się panoramą i bywa najczęściej stosowane w rysunkach architektonicznych i w wizualizacji danych. Rzadziej są stosowane rzuty na powierzchnie nierozwijalne, np. olorama, czyli rzut na sferę. Odwzorowanie obrazu na sferze (lub innej powierzchni nierozwijalnej) w płaszczyznę wprowadza dodatkowe zniekształcenia, które utrudniają jego oglądanie.