Innym sposobem wprowadzenia pewnej zależności od wieku jest modelowanie przy użyciu równań z opóźnieniem. Wróćmy do opisu dynamiki populacji za pomocą wzoru (2.1) i załóżmy, że przyrost per capita zależy nie od liczebności populacji w bieżącej chwili t, ale od stanu w pewnej chwili w przeszłości t-τ. Kiedy tak się będzie działo? Wyobraźmy sobie populację roślinożerców, które zjadają rośliny będące w pewnym konkretnym wieku τ i jest to jednocześnie wiek, w którym te rośliny rozsiewają nasiona. Jeśli roślina zostanie zjedzona, to nie rozsieje nasion, a wtedy w przyszłości osobniki opisywanej populacji nie mają co jeść. Ilość zjedzonych roślin zależy od stanu populacji w bieżącej chwili, zatem ilość jedzenia w przyszłości, czyli przyrost per capita, zależy od tego stanu. Przy takich założeniach równanie na przyrost per capita przyjmuje postać

W szczególności równanie logistyczne z opóźnieniem zaproponowane przez G. E. Hutchinsona w 1948 r. zapiszemy jako

Oczywiste jest, że przy opisanym powyżej modelu heurystycznym powinniśmy rozważać nie dokładnie jedno ustalone opóźnienie τ, ale pewien rozkład opóźnienia, gdyż nie ma w naturze takich roślin, które rozsiewałyby nasiona dokładnie w danym wieku, ale jak zwykle staraliśmy się zbudować jak najprostszy model, zatem przyjęliśmy uproszczenie polegające na ustaleniu opóźnienia τ.

Chcemy zbadać zależność rozwiązań równania (5.1) od wielkości opóźnienia τ>0. Zajmiemy się najpierw omówieniem podstawowych własności, takich jak istnienie, jednoznaczność i nieujemność rozwiązań dla nieujemnego warunku początkowego. Zauważmy, że aby rozwiązać równanie z opóźnieniem τ nie wystarczy, że określimy początkową liczebność populacji N⁢0=N0, ale musimy zadać funkcję początkową określoną na przedziale długości opóźnienia, czyli N0:-τ,0→R+. Typowo w teorii równań różniczkowych z opóźnionym argumentem zakładamy, że funkcja początkowa jest ciągła, ale nie zawsze jest to założenie konieczne. W szczególności — znając funkcję początkową N0 możemy rozwiązać równanie (5.1) metodą kroków, o ile tylko funkcja początkowa jest całkowalna. Dokładniej, niech t∈0,τ. Wtedy

czyli

Oznaczmy otrzymane rozwiązanie przez N1⁢t=N0⁢0⁢exp⁡r⁢t-rK⁢∫-τt-τN0⁢s⁢d⁢s dla t∈0,τ. Zauważmy, że jest ono dobrze określone dla ciągłej funkcji początkowej, co więcej w tym przypadku wystarczy, żeby funkcja N0 była całkowalna. Mamy też jednoznaczność, a nieujemność wynika z nierówności N0⁢0≥0, przy czym N0⁢0=0 implikuje N⁢t≡0 (stany stacjonarne równań z opóźnieniem są oczywiście takie same jak dla analogicznego równania bez opóźnienia, skoro nie zależą one od czasu). Teraz zastosujemy metodę indukcji matematycznej. Załóżmy, że znamy rozwiązanie Nk⁢t na przedziale k-1⁢τ,k⁢τ i znajdźmy rozwiązanie na kolejnym przedziale

Wobec tego metoda indukcji matematycznej gwarantuje, że rozwiązanie istnieje dla dowolnego t≥0 i ma pożądane własności.

Zbadamy teraz własności asymptotyczne rozwiązań, w szczególności stabilność lokalną rozwiązań stacjonarnych. Metoda badania stabilności jest analogiczna, jak stosowana w przypadku równań bez opóźnienia. Przeprowadzamy najpierw linearyzację wokół stanu stacjonarnego. Niech N¯ będzie rozwiązaniem stacjonarnym, czyli N¯=0 albo N¯=K. Wprowadzamy nową zmienną x⁢t, która oznacza odchylenie od stanu stacjonarnego, N⁢t=N¯+x⁢t, przy czym zakładamy, że x⁢t<ε i pomijamy wyrazy rzędu ε2. Mamy

po pominięciu składnika -r⁢x⁢t⁢x⁢t-τK i zauważeniu, że r⁢N¯⁢1-N¯K=0 dla obu stanów stacjonarnych.

Dla stanu stacjonarnego N¯=0 równanie zlinearyzowane ma postać

Widzimy więc, że odchylenie od stanu stacjonarnego x⁢t rośnie, zatem N¯=0 jest niestabilne.

Z kolei dla dodatniego stanu stacjonarnego

Jak zbadać stabilność stanu stacjonarnego x¯=0 powyższego równania? Tak jak w przypadku równań bez opóźnienia szukamy rozwiązań w postaci wykładniczej x⁢t=x0⁢eλ⁢t. Jeśli wszystkie wartości własne λ mają części rzeczywiste ujemne, to x⁢t→0 przy t→+∞ dla dostatecznie małych x0. Stąd odchylenie maleje do 0, zatem stan N¯=K równania (5.1) jest lokalnie asymptotycznie stabilny. Jeśli natomiast istnieje wartość własna o części rzeczywistej dodatniej, to N¯=K jest niestabilny. Okazuje się, że dla równań z opóźnieniem równanie charakterystyczne, w tym przypadku

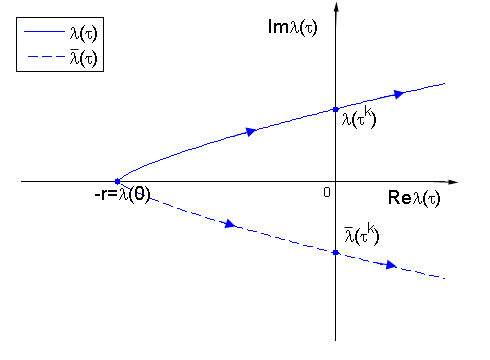
ma nieskończenie wiele rozwiązań, które zależą w sposób ciągły od parametrów, w szczególności od opóźnienia. Skoro dla τ=0 mamy λ=-r<0, to dla małych opóźnień stan N¯=K pozostaje stabilny. Zastanówmy się kiedy może nastąpić destabilizacja. Skoro niestabilność wiąże się z pojawieniem się wartości własnej o dodatniej części rzeczywistej, to dla pewnej krytycznej wartości τk>0 musimy mieć λ=±i⁢ω, ω>0, i wartości własne przechodzą z lewej półpłaszczyzny zespolonej na prawą, więc d⁢ℜ⁡λd⁢ττ=τk>0, gdzie ℜ⁡λ oznacza część rzeczywistą wartości własnej, por. rys. 5.1.

Jeśli λ=±i⁢ω, to

ale e∓i⁢ω⁢τk=1, więc ωk=r (w ogólnym przypadku łatwiej rozpatrywać tę równość po podniesieniu do kwadratu). Znając krytyczną wartość własną obliczamy τk

czyli cos⁡ωk⁢τk=0 i sin⁡ωk⁢τk=1, wobec tego ωk⁢τk=π2+2⁢n⁢π, n∈N. Mamy więc ciąg krytycznych wartości własnych τnkn=0∞. Okazuje się, że znak d⁢ℜ⁡λd⁢ττ=τk możemy sprawdzić korzystając z już przeprowadzonych obliczeń. W ogólnym przypadku dla układu równań z pojedynczym opóźnieniem τ równanie charakterystyczne ma postać

i dla czysto urojonych wartości własnych λ=i⁢ω, ω>0, definiujemy funkcję pomocniczą

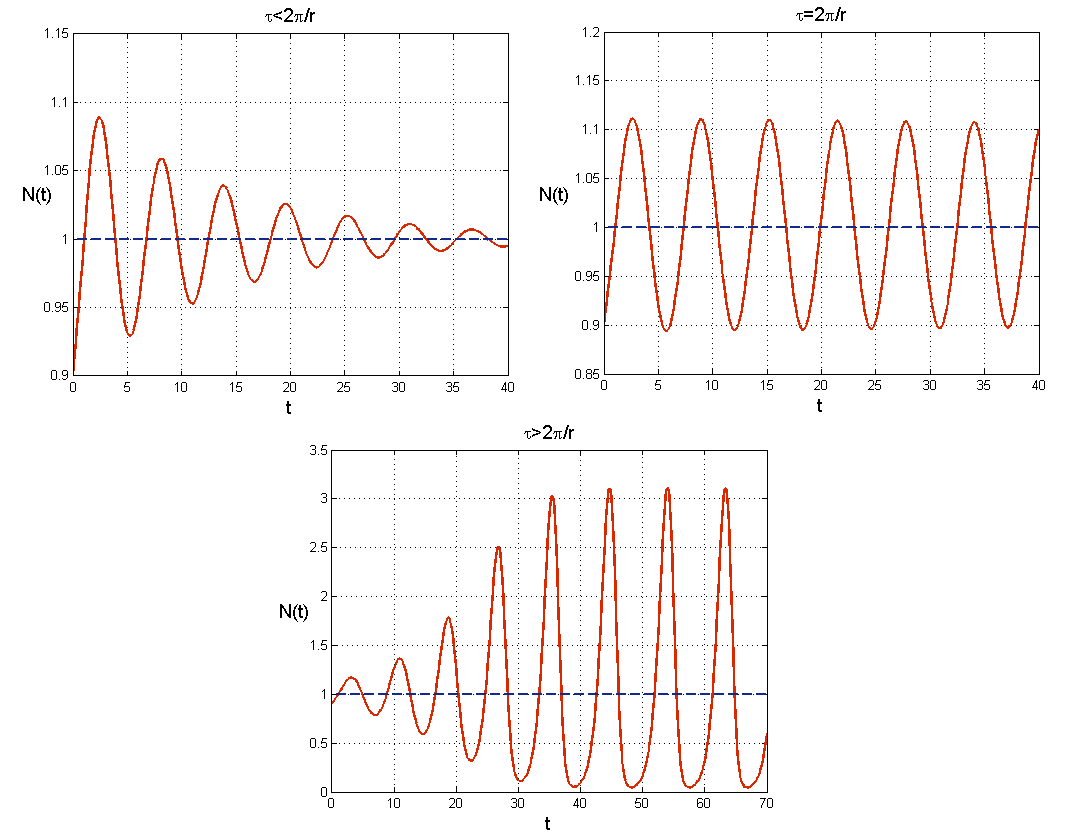
której miejsca zerowe wyznaczają czysto urojone wartości własne. U nas F⁢ω=ω2-r2. Podstawiamy y=ω2 i rozpatrujemy F~⁢y=y-r2. Pochodna tej funkcji w punkcie y=ωk2 ma taki sam znak jak d⁢ℜ⁡λd⁢ττ=τk. W naszym przypadku F~′⁢y=1>0, zatem zawsze wartości własne przechodzą z lewej półpłaszczyzny na prawą. Wobec tego dla pierwszej wartości krytycznej τ0k=π2⁢r następuje destabilizacja i rozwiązanie N¯=K pozostaje niestabilne dla wszystkich τ>τ0k. Ten mechanizm destabilizacji nazywamy bifurkacją Hopfa. W jej wyniku pojawiają się nietrywialne rozwiązania okresowe o okresie 2⁢πωk=2⁢πr, co widzimy na wykresach na rys. 5.2.

Podsumowując tę tematykę należy stwierdzić, że wprowadzenie do opisu heurystycznego zależności od wieku prowadzi najczęściej do dynamiki oscylacyjnej, która jest zwykle obserwowana w przypadku populacji występujących w naturze. Widzimy też, że opis dynamiki za pomocą równań z opóźnieniem może przypominać zachowanie rozwiązań modeli dyskretnych, gdzie też obserwujemy oscylacje. Co więcej, jeśli prawa strona równania z opóźnieniem reprezentuje np. funkcję Hilla, to dla odpowiednio dużych wartości współczynnika Hilla występują zachowania chaotyczne, znów analogicznie jak w modelach dyskretnych. Możemy przypuszczać, że podobieństwa te wiążą się z podobną strukturą obu typów modeli — w modelach dyskretnych tak jak w równaniach z opóźnieniem dynamika w chwili bieżącej t zależy od stanu układu z chwili poprzedniej t-1.