Zagadnienia

2.1 Relacje preferencji ponownie

2. Ogólna teoria wyboru – ciąg dalszy

2.1. Relacje preferencji ponownie

Oprócz wymienionej poprzednio racjonalności, relacje preferencji mogą jeszcze inne własności, przydatne w późniejszych rozważaniach. Odtąd zakładamy, że relacja preferencji jest racjonalna.

Zdefiniujemy je poniżej:

Definicja 2.1

Relację preferancji ⪰ nazywamy:

a) ciągłą, jeśli dla każdego x∈ X zbiory y∈X:x⪰y i y∈X:y⪰x są domknięte;

b) monotoniczną, jeśli x≥y⟹x⪰y;

c) ściśle monotoniczną, jeśli (x≥y∧x≠y)⟹x≻y;

d) lokalnie nienasyconą, jeśli w dowolnym otoczeniu punktu x istnieje y lepszy od x (formalnie ∀x∈X,ϵ>0 ∃y∈X taki że y-x<ϵ i y≻x);

e) wypukłą, jeśli ∀(x,y,z∈X,0<t<1) (x⪰z∧y⪰z)⟹tx+(1-t)y⪰z (dla każdego z zbiór punktów niegorszych od z jest wypukły);

f) ściśle wypukłą, jeśli ∀(x,y,z∈X,0<t<1) (x⪰z∧y⪰z∧x≠y)⟹tx+(1-t)y≻z.

Monotoniczność oznacza, że mamy do czynienia z dobrami a nie ”złem”, to znaczy że są one pożądane, ścisła monotoniczność oznacza ponadto, że nie występuje punkt nasycenia. Lokalne nienasycenie gwarantuje, że krzywe obojętności nie mogą być ”grube”.

Ćwiczenie 2.1

Zbadać które z powyższych własności mają relacje preferencji opisane werbalnie w zadaniu 1.9.

Ćwiczenie 2.2

Ania wydaje cały swój miesięczny dochód na szarlotkę i lody.

Lipiec spędziła w Koszalinie, a sierpień w Pruszkowie. W Koszalinie szarlotka kosztowała 8zł, a lody 6, natomiast w Pruszkowie szarlotka 3, a lody 4. W Koszalinie Ania zjadła 3 porcje szarlotki i 4 lodów, a w Pruszkowie na odwrót.

Po wakacjach stwierdziła, że jej satysfakcja z konsumpcji była identyczna w obu miejscach.

Czy jej postępowanie można opisać ściśle monotonicznymi, ciągłymi, ścisle wypukłymi preferencjami?

Stwierdzenie 2.1

a) Jeśli istnieje ciągła funkcja użyteczności odzwierciedlająca ⪰, to relacja ⪰ jest ciągła.

b) Jeśli istnieje, wklęsła (ściśle wklęsła) funkcja użyteczności odzwierciedlająca ⪰, to relacja ⪰ jest wypukła (ściśle wypukła).

c) Jeśli istnieje monotoniczna (ściśle monotoniczna) funkcja użyteczności odzwierciedlająca ⪰, to relacja ⪰ jest monotoniczna (ściśle monotoniczna).

d) Każda funkcja odzwierciedlająca monotoniczne (ściśle monotonicze) preferencje jest ściśle monotoniczna.

Ćwiczenie 2.3

Udowodnić stwierdzenie.

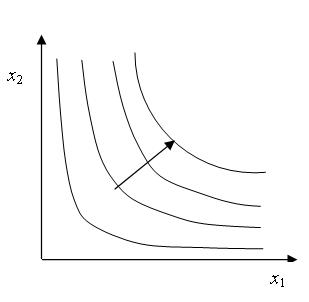
Zazwyczaj stosowane w ekonomii (głównie w zagadnieniu optymalizacji konsumenta) relacje preferencji są ciągłe, ściśle monotoniczne i ściśle wypukłe, a odpowiadające im funkcje użyteczności gładkie.

Typowa mapa obojętności (rysunek przedstawiający różne krzywe obojątności na płaszczyźnie) wygląda więc tak, jak na rysunku 2.1.

Rys. 2.1. Preferencje ściśle monotoniczne, ściśle wypukłe, ciągłe i lokalnie nienasycone.

Przykład 2.1

Przykłady relacji preferencji i funkcji użyteczności w R+2:

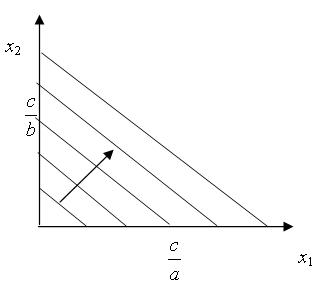
a) doskonałe substytuty – z dokładnością do przeskalowania są swoimi zamiennikami (np. banknoty o różnych nominałach; takie same gwoździe z dwóch różnych sklepów): x1,x2⪰y1,y2⇔a⁢x1+b⁢x2≥a⁢y1+b⁢y2;

Rys. 2.2. Dobra doskonale substytucyjne.

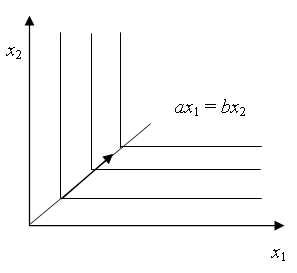
b) dobra doskonale komplementarne – zużywane zawsze w równych proporcjach, nadmiar się marnuje (np. prawe i lewe buty, czy składniki kleju dwuskładnikowego) x1,x2⪰y1,y2⇔min⁡a⁢x1,b⁢x2≥min⁡a⁢y1,b⁢y2;

Rys. 2.3. Dobra doskonale komplementarne.

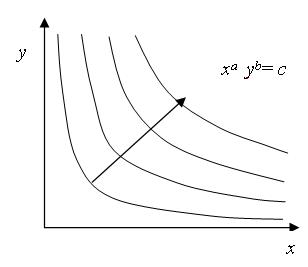
c) funkcja użyteczności Cobba-Douglasa u⁢x,y=xa⁢yb.

Rys. 2.4. Prefernecje Cobba-Douglasa.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Skrypt do wykładu z mikroekonomii dla wydziału MIMUW 2009/2010