Zagadnienia

4.1 Odwzorowania wielowartościowe
4.2 Punkty stałe

4. Narzędzia – ciąg dalszy

4.1. Odwzorowania wielowartościowe

Ponieważ będziemy rozpatrywać zagadnienie optymalizacyjne w zmieniających się warunkach, zbiory budżetowe, jak również zbiory optymalnych wyborów będą się zmieniać. Jeżeli będzie nas interesować zależność od parametrów, będziemy mieć do czynienia z funkcją. Jednakże wartościami tej funkcji będą przeważnie zbiory. W zasadzie funkcja o wartościach w przestrzeni zbiorów nie jest niczym strasznym, jednak jak np. narysować jej wykres? Jak łatwo stwierdzić, czy jest ona ciągła? Jest na to sposób, bez uciekania się do topologii ogólnej.

Przypomnienie ze wstępu do matematyki: ”funkcja jest to odwzorowanie wielowartościowe (relacja), które…”

Wrócimy do korzeni, czyli do odwzorowań wielowartościowych.

Definicja 4.1

Odwzorowanie wielowartościowe Γ:A⊸B, to dowolna funkcja ze zbioru A w zbiór potęgowy zbioru B (równoważnie jest to dowolny podzbiór zbioru A×B).

WykresemΓ nazywamy zbiór a,b∈A×B:b∈Γ⁢a.

Przeciwobrazem górnym zbioruB∈B nazywamy zbiór a∈A:Γ⁢a⊂B, a przeciwobrazem dolnym zbioru B∈B nazywamy zbiór a∈A:Γ⁢a∩B≠∅.

Odwzorowanie Γ nazywamy półciągłym z góry (z dołu), jeśli przeciwobrazy górne (dolne) zbiorów otwartych są otwarte.

Odwzorowanie Γ nazywamy ciągłym, jeśli jest równocześnie półciągłe z góry i z dołu.

Niech X=Rn i odwzorowanie Γ:X⊸R. Odwzorowanie Γ nazywamy (dodatnio) jednorodnym stopnia r, jeżeli dla każdego x∈X, y∈R, t>0 mamy y∈Γ⁢x⇔tr⁢y∈Γ⁢t⁢x.

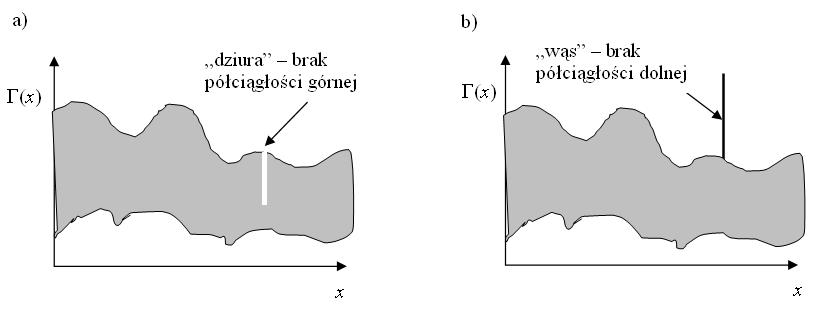
Obrazowo mówiąc, półciągłość górna oznacza, że wykres nie ma ”dziur”, a dolna, że ”wąsów”.

Rys. 4.1. Najprostsze przykłady braku półciągłości.

Łatwo zauważyć, że jeśli odwzorowanie Γ jest jednowartościowe (czyli jest ”zwykłą” funkcją), to jego dowolna półciągłość jako odwzorowania, implikuje ciągłość jako funkcji.

Ćwiczenie 4.1

Jakie relacje inkluzji zachodzą pomiędzy:

a) Γ+⁢A∪B a Γ+⁢A∪Γ+⁢B;

b) Γ+⁢A∩B a Γ+⁢A∩Γ+⁢B;

c) Γ+⁢∖A a ∖Γ+⁢A;

d) Γ+⁢∖A a ∖Γ-⁢A;

e) i analogicznie dla Γ-.

Ćwiczenie 4.2

Niech f:R→R będzie funkcją ciągłą.

Narysować wykres i zbadać ciągłość odwzorowania Γ:R⊸R zdefiniowanego przez

a) Γ⁢x=y:f⁢x≤y;

b) Γ⁢x=y:f⁢y≤x;

c) Γ⁢x=y:f⁢x≤f⁢y;

a) Γ⁢x=y:f⁢x<y.

Twierdzenie 4.1

(twierdzenie o maksimum)

Jeżeli funkcja f:A×B→R jest ciągła, a odwzorowanie Γ:A⊸B jest ciągłe i ma niepuste, zwarte wartości, to odwzorowanie Γ~:A⊸B określone wzorem Γ~⁢x=Argmaxy∈Γ⁢xf⁢x,y jest górnie półciągłe, a funkcja M⁢x=maxy∈Γ⁢x⁡f⁢x,y jest ciągła.

4.2. Punkty stałe

W zagadnieniach równowagi ogólnej będę nam potrzebne twierdzenia o punkcie stałym, które nie wchodzą w zakres podstawowego kursu topologii.

W przypadku, gdy mamy do czynienia z funkcją, punkt stały jest to taki punkt, który jest równy swojej wartości przy tej funkcji.

Twierdzenie 4.2

(twierdzenie Brouwera o punkcie stałym)

Jeżeli K⊂Rn jest zbiorem niepustym, zwartym i wypukłym a funkcja f:K→K jest ciągła, to istnieje x∈K, takie że x=f⁢x.

Istnieją też inne sformułowania twierdzenia Brouwera, w których K jest kulą lub sympleksem.

W przypadku odwzorowań wielowartościowych punkt stały to punkt, który należy do swojej wartości.

Twierdzenie 4.3

(twierdzenie Kakutaniego o punkcie stałym)

Jeżeli K⊂Rn jest zbiorem niepustym, zwartym i wypukłym a odwzorowanie Γ:K⊸K o niepustych, zwartych, wypukłych wartościach jest górnie półciągłe lub ma wykres domknięty, to istnieje x∈K, takie że x∈Γ⁢x.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Skrypt do wykładu z mikroekonomii dla wydziału MIMUW 2009/2010