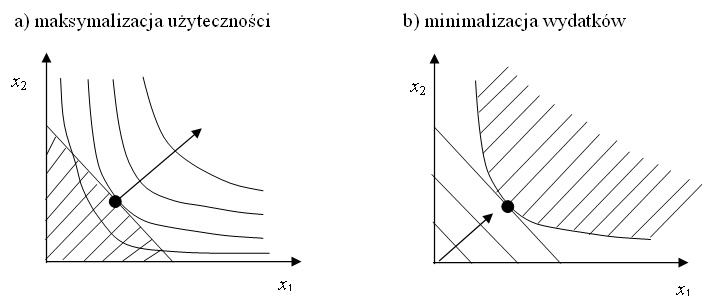
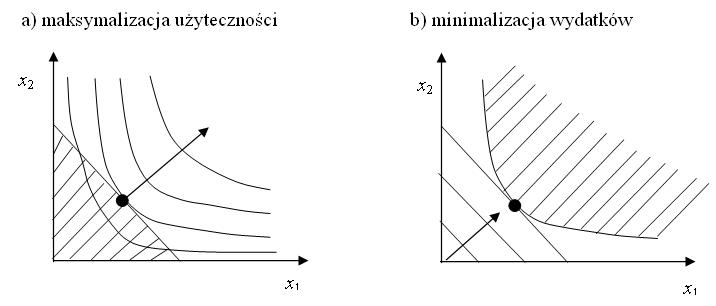
6.1. Minimalizacja wydatków
Na optymalizację konsumenta możemy też spojrzeć z drugiej
strony: zamiast maksymalizować użyteczność przy zadanym
dochodzie, jaki możemy przeznaczyć na konsumpcję, dążyć do osiągnięcia przynajmniej takiej użyteczności
jak najmniejszym kosztem.
Definicja 6.1
Funkcję e:IntR+n×R→R+ zdefiniowaną wzorem ep,u¯=infux≥u¯pTx (gdzie przez infx∈∅fx rozumiemy +∞) nazywamy funkcją wydatków (expenditure
function), a odwzorowanie h:IntR+n×R→X zdefiniowane wzorem hp,u¯=Argminux≥u¯pTx odwzorowaniem popytu Hicksa
(czasem także odwzorowaniem popytu skompensowanego dochodu).
Funkcja wydatków określa, ile minimalnie muszę wydać, aby
przy cenach p móc zapewnić sobie konsumpcję o
użyteczności u¯.
Stwierdzenie 6.1
Jeżeli u jest ciągła, to odwzorowanie popytu Hicksa ma niepuste
wartości, a funkcja wydatków jest skończona dla dowolnego u¯<supx∈Xux.
Zbiór A=x∈R+n:ux≥u¯
jest w tej sytuacji niepusty, domknięty. Niech pewien x¯ nalezy
do tego zbioru. Wówczas zbiór A∩x∈R+n:x≤x¯ jest niepusty, zwarty, a ponieważ wszystkie pi>0, Argminx∈ApTx=Argminx∈A∩x∈R+n:x≤x¯pTx. Mamy więc problem
minimalizacji funkcji ciągłej na zbiorze zwartym.
∎
Stwierdzenie 6.2
Własności popytu Hicksa.
a) Jeśli funkcja użyteczności jest quasi-wklęsła to
odwzorowanie popytu Hicksa h ma wartości wypukłe, a jeżeli jest
ściśle quasi-wklęsła, to h jest co najwyżej
jednowartościowe;
b) Jeśli preferencje są monotoniczne, lokalnie nienasycone a u
jest ciągła, to nie ma nadmiarowej użyteczności, tzn.
dla u¯≥infuX jeśli x∈hp,u¯, to
ux=u¯;
c) Dla ustalonego u¯ odwzorowanie h(⋅,u¯) jest jednorodne
stopnia 0 jako odwzorowanie p;
d) Odwzorowanie popytu Hicksa przy ustalonym u¯ h(⋅,u¯)
jest ciągłe jako odwzorowanie p, a jeśli funkcja u
jest ciągła, lokalnie nienasycona, to h obcięte do zbioru p,u¯:u¯<supx∈Xux jest
górnie półciągłe łącznie ze względu na wszystkie
zmienne.
Stwierdzenie 6.3
Własności funkcji wydatków.
a) Funkcja e jest niemalejącą funkcją p i u¯, a
jeśli preferencje są monotoniczne, lokalnie nienasycone i u jest ciągła, to ściśle rosnącą u¯ dla u¯<supx∈Xux;
b) Funkcja e jest jednorodna stopnia 1 ze względu na p;
c) Funkcja e jest wklęsła ze względu na p;
d) Funkcja e przy ustalonym u¯ e(⋅,u¯) jest ciągła ze względu na p, a jeśli funkcja u jest ciągła,
lokalnie nienasycona, to e obcięta do zbioru p,u¯:u¯<supx∈Xux jest ciągła łącznie ze
względu na wszystkie zmienne.
e) Jeśli preferencje są monotoniczne, lokalnie nienasycone, a u
jest, ciągła, to limu¯→supx∈Xuxep,u¯=+∞.
(obu stwierdzeń:)
Punkty 6.2 a) i c) oraz
6.3 a) i b) są natychmiastowe. Pozostaje więc
udowodnić pozostałe pięć.
6.3 c) Weźmy dowolne wektory cen p i p′ i t∈0,1.
Niech p′′=tp+1-tp′. ep′′,u¯=minx:ux≥u¯p′′Tx=minx:ux≥u¯tp+1-tp′Tx≥
≥tminx:ux≥u¯pTx+(1-t)minx:ux≥u¯(p′)Tx=te(p,u¯)+(1-t)e(p′,u¯).
6.2 b) Minimum funkcji liniowej na zbiorze może być
przyjmowane jedynie na jego brzegu. Ponieważ preferencje są
monotoniczne, lokalnie nienasycone, więc poza u¯≤minuX nie będzie to 0. Niech więc punkt x¯, w
którym jest przymowane minimum będzie punktem z brzegu zbioru x:ux≥u¯ i niech ux¯>u¯. Wówczas dla
pewnego małego ε, z ciągłości u w pewnym
otoczeniu x¯ istnieje taki x≤x¯ z przynajmniej jedną
nierównością ostrą, dla którego ux>ux¯-ε>u¯. Z nierówności na współrzędnych pTx<pTx¯ – sprzeczność.
6.3 e) Weźmy ciągi xkT=kp1,…,kpn i uk=uxk. Niech yk∈hp,uk.
Ponieważ preferencje są monotoniczne, lokalnie nienasycone,
przynajmniej jedna współrzędna yk musi być co namniej
równa analogicznej współrzędnej xk, co daje
pTyk≥k, czyli ep,uk≥k. Stąd i z tego,
że e jest ściśle rosnąca po u¯ dostajemy limu¯→supx∈Xuxep,u¯≥limk→∞ep,uk=+∞.
6.2 d) i 6.3 d) dowodzimy łącznie z
twierdzenia o maksimum 4.1.
Najpierw dla ustalonego u¯. Odwzorowanie Γ, które przyporządkowuje p zbiór x:ux≥u¯ jest
niezależne od p, a więc jest ciągłe (przeciwobrazem
dowolnego rodzaju dowolnego zbioru otwartego jest albo ∅ albo
całe IntR+n – otwarte). W twierdzeniu o maksimum
potrzebujemy jednak dodatkowo zwartych wartości. Aby to uzyskać,
musimy ograniczyć się – przynajmniej lokalnie do szukania minimum
na zbiorze zwartym. Weźmy zatem dowolne x¯ dla którego ux¯≥u¯.
Jeśli ograniczymy się do zbioru A=x:ux≥u¯∩x:pTx≤M dla M>∑i=1npi+δx¯i, to dla p′
bliskich p: takich, że dla każdego i pi-pi′<δ zachodzi Argminux≥u¯p′Tx=Argminx∈Ap′Tx, a więc sprowadziliśmy nasze zagadnienie
do zagadnienia maksymalizacji po zbiorach zwartych, niezależnych od p, tak więc mamy tezę z twierdzenia o maksimum.
Teraz zajmiemy się globalną ciągłością. Aby to
uzyskać, musimy pokazać ciągłość odwzorowania,
oznaczmy je przez Γ, które przyporządkowuje p,u¯ zbiór x:ux≥u¯. Dodatkowo podobnie będziemy musieli uzwarcić wartości – podobnie jak poprzednio. Dalszy
schemat dowodu podobny do dowodu stwierdzeń 5.1 d) i 5.2 d).
∎
Stwierdzenie 6.4
(Lemat Shepharda)
Jeżeli funkcja użyteczności jest różniczkowalna,
monotoniczna, lokalnie nienasycona, a odwzorowanie popytu Hicksa h jest
funkcją różniczkowalną po p; u<supx∈Xux , pi>0 dla każdego i oraz mnożnik Lagrange'a
λp,u¯ jest jednoznacznie wyznaczony, to jeśli
dla każdego i hip,u>0, to
a) hip,u¯=∂ep,u∂pi,
b) jeżeli ponadto funkcja h jest różniczkowalna jako funkcja p, macierz ∂hi∂pj
jest symetryczna, niedodatnio określona, w szczególności ∂hi∂pi≤0 (tzw. ujemny efekt cenowy Hicksa).
a) Wynika natychmiast z zastosowania twierdzenia o
obwiedni.
b) Uzyskujemy, różniczkując e po p dwukrotnie – z
a) i wklęsłości e po p.
∎
Ćwiczenie 6.1
Obliczyć funkcję wydatków i odwzorowanie popytu Hicksa dla ux1,x2 równej
a) a1⋅x1+a2⋅x2 przy ai>0 (doskonałe substytuty);
b) mina1⋅x1,a2⋅x2 przy ai>0 (dobra doskonale komplementarne);
c) x1a1⋅x2a2 przy ai>0 (użyteczność Cobba-Douglasa).
Odwzorowania popytu Hicksa, nawet jeśli nie są funkcjami
różniczkowalnymi mają ponadto tę interesującą własność, że popyt zmienia się ”w kierunku przeciwnym do
zmiany ceny”. Formalnie zachodzi następujący fakt:
Stwierdzenie 6.5
Jeśli hp,u¯∩hp′,u¯=∅, to dla każdego x∈hp,u¯, x′∈hp′,u¯ zachodzi
nierówność (p′-p)T(x′-x)<0.
Rozłóżmy p′-pTx′-x=p′Tx′-p′Tx+pTx-pTx′.
Pierwszy nawias jest ujemny, ponieważ minimum p′Tx na zbiorze x:ux≥u¯ jest przyjmowane na hp′,u¯, a x′ nie należy do hp′,u¯, drugi analogicznie.
∎
6.2. Związki pomiędzy zagadnieniami maksymalizacji
użyteczności i minimalizacji wydatków
Zagadnienia maksymalizacji użyteczności i minimalizacji wydatków
są względem siebie dualne.
Aby zachodził poniższy fakt, nie potrzeba pełnych założeń
modelu konsumenta
Stwierdzenie 6.6
Jeżeli
preferencje są lokalnie nienasycone, ciągłe i u¯∈uX, to:
a) vp,ep,u¯=u¯;
b) xip,ep,u¯=hip,u¯ dla i=1,…,n;
c) ep,vp,m=m;
d) hip,vp,m=xip,m dla i=1,…,n.
Ćwiczenie 6.2
O ileż prościej byłoby rozwiązać zadanie 6.1 korzystając z dualności!
Ćwiczenie 6.3
Mamy daną funkcję vp1,p2,m=m2p1+p22.
Czy może być ona niejawną funkcją użyteczności przy standartowych założeniach modelu konsumenta?
Obliczyć (zakładając, że nasze postępowanie jest poprawne), oba odzworowania popytu i funkcję wydatków.
Jaka jest wyjściowa funkcja u?
Ćwiczenie 6.4
Mamy daną funkcję ep1,p2,u¯=p1⋅p2⋅u¯.
Czy może być ona funkcją wydatków przy standartowych założeniach modelu konsumenta?
Obliczyć niejawną funkcję użyteczności oraz, zakładając, że nasze postępowanie jest poprawne, oba odzworowania popytu.