Zagadnienia

5.1 Co się pod tym kryje
5.2 Podejście maksymalizacji użyteczności w modelu konsumenta

5. Teoria wyboru konsumenta – maksymalizacja użyteczności

5.1. Co się pod tym kryje

Kto to jest konsument? Choć by sformułować jego zagadnienie optymalizacyjne nie potrzebujemy dokładnej interpretacji, lepiej zawsze wiedzieć, co będziemy rozumieć przez omawiany teoretyczny obiekt.

Otóż konsumentami jesteśmy my wszyscy w większości codziennych wyborów, nie tylko w restauracji czy sklepie spożywczym. Konsumentem jest klient kancelarii adwokackiej, podróżujący koleją, kupujący lodówkę, kwiaty albo bilet do opery, wpłacający pieniądze do banku… Dowolny nadywca dóbr lub usług. W mikroekonomii nie będziemy rozróżniali pomiędzy tymi dwoma pojęciami i określimy je łącznym pojęciem ”dobra”.

Co więcej, konsumentami jesteśmy nawet, kiedy leżymy pod gruszą i nic nie robimy: wówczas konsumujemy czas wolny!

Teraz sformalizujemy zagadnienie optymalizacji konsumenta. Konsument jest podejmującym decyzję, więc cała streszczona uprzednio teoria wyboru ma zastosowanie.

Zbiór możliwości konsumenta określamy mianem zbioru konsumpcji. Zakładamy, że wszystkie współrzędne (których może być nawet nieskończenie wiele) jego elementów są nieujemne i zazwyczaj mogą być dowolnie duże. W praktyce będziemy zakładać, że mamy do czynienia z $n$ dobrami, a więc $\mathbb{X}=\mathbb{R}_{{+}}^{{n}}$ . Elementy zbioru konsumpcji nazywamy koszykami (czasem też używa się słowa wiązka).

Zbiory budżetowe mogą być różne w różnych sytuacjach, jednak w standartowych zastosowaniach będą to walrasowskie zbiory budżetowe $B_{{\mathbf{p},m}}=\{ x\in\mathbb{X}:x^{{T}}\mathbf{p}\leq m\}$ .

5.2. Podejście maksymalizacji użyteczności w modelu konsumenta

Do zdefiniowania w pełni zagadnienia optymalizacyjnego pozostało nam jeszcze określić relację preferencji konsumenta. Skoro używamy słowa ”dobra”, naturalnym założeniem jest, aby nie były one ”złem”, czyli aby relacja preferenecji była monotoniczna. Jak to uzyskać, jeśli rozważamy np. zagadnienie wyboru długości czasu pracy albo poziomu zanieczyszczeń? – Wystarczy złożyć ”zło” z funkcją ściśle malejącą np. odjąć liczbę przepracowanych godzin od maksymalnego możliwego czasu pracy – wówczas otrzymamy już rzeczywiste dobro – odpoczynek.

Zakłada się również, że konsument nigdy nie jest nasycony i że zawsze ”w dowolnie małym zasięgu ręki” znajduje się koszyk lepszy, a więc relacja preferencji jest lokalnie nienasycona.

Przeważnie przyjmujemy również ścisłą monotoniczność (nie jest to spełnione np. przez dobra doskonale komplementarne) i wypukłość (co implikuje, że koszyk ”pośredni” będący kombinacją wypukłą dwóch koszyków o jednakowej wartości jest od nich niegorszy), a nawet ścisłą wypukłość (co implikuje, że koszyk ”pośredni” jest lepszy). Co więcej, zazwyczaj będziemy pracować z wklęsłą, różniczkowalną funkcją użyteczności.

Odtąd przez założenia standartowe modelu konsumenta będziemy rozumieć, że preferencje są lokalnie nienasycone, monotoniczne, ciągłe, wypukłe, a jeśli mówimy o konkretnej odzwierciedlającej je funkcji użyteczności, to zakładamy ponadto, że jest ciągła.

Przy tych założeniach do znalezienia punktów optymalnych możemy stosować, jak w przykładzie 3.1, mnożniki Lagrange'a.

Odtąd będziemy rozważać zbiór konsumpcyjny $\mathbb{X}=\mathbb{R}_{{+}}^{{n}}$ , walrasowskie zbiory budżetowe $B_{{\mathbf{p},m}}=\{ x\in\mathbb{R}_{{+}}^{{n}}:\mathbf{p}^{{T}}x\leq m\}$ dla wektora $\mathbf{p}$ o wszystkich współrzędnych dodatnich i quasi wklęsłą ciąglą niemalejącą funkcję użyteczności $u$ .

Dlaczego zakładamy, że ceny są ściśle dodatnie? Co by było gdyby ceny były zerowe: czekolada na gorąco w Kubusiu za darmo – po pierwsze nie opłacałoby się jej sprzedawać… Czasem jednak zdarza się że ceny są zerowe – chociażby za powietrze nie musimy płacić. To ma sens, jeżeli dobro, które rozważamy nie jest rzadkie – wówczas po prostu nie ma możliwości nadmiernego wykorzystania. W przeciwnym przypadku powstają tak zwane efekty zewnętrzne – inni ponoszą konsekwecje naszego zachowania. Tę kwestię poruszymy jeszcze raz dokładniej przy okazji podejmowania decyzji przez producenta.

Przyjęcie walrasowskiego zbioru budżetowego, oznacza, że zakładamy, że konsument dysponuje dochodem $m$ i przyjmuje ceny $\mathbf{p}$ (dodatnie) jako dane, czyli jest ”biorcą cen” – przy optymalizacji nie bierze pod uwagę swojego wpływu na ceny.

Tak więc, jak w ogólnej teorii wyboru, będziemy rozważać następującą sytuację: dla każdego zbioru budżetowego konsument maksymalizuje swoją użyteczność na tym zbiorze. Ponieważ rodzina zbiorów budżetowych jest indeksowana poziomem cen i dochodem, możemy patrzeć zarówno na wybór w konkretnej sytuacji, jak i na samą użyteczność wybranego koszyka, jako na funkcję tych dwóch parametrów.

Definicja 5.1

Funkcję $v:\mathop{\rm{Int}}\mathbb{R}_{{+}}^{{n}}\times\mathbb{R}_{{+}}\rightarrow\mathbb{R}$ zdefiniowaną wzorem $v(\mathbf{p},m)=\max _{{\mathbf{p}^{{T}}x\leq m}}u(x)$ nazywamy niejawną funkcją użyteczności (indirect utility function), a odwzorowanie $x:\mathop{\rm{Int}}\mathbb{R}_{{+}}^{{n}}\times\mathbb{R}_{{+}}\rightarrow\mathbb{X}$ zdefiniowane wzorem $x(\mathbf{p},m)=\mathop{\rm{Argmax}}_{{\mathbf{p}^{{T}}x\leq m}}u(x)$ odwzorowaniem popytu (także odwzorowaniem popytu Marshalla, albo Walrasa ).

Będą nas interesować własności zdefiniowanych obiektów.

Oczywistym jest, że przy standartowych założeniach $x$ ma niepuste wartości.

Niejawna funkcja użyteczności może być traktowana jako obiekt teoretyczny, ponieważ, podobnie jak w przypadku funkcji użyteczności, trudno jest przypisać konkretne wartości liczbowe, jednak istotne są jej własności porządkowe: większa wartość niejawnej funkcji użyteczności oznacza, że sytuację, czyli zbiór budżetowy, uważamy z lepszą. Czyli ankiety z pytaniami postaci ”czy uważa pan/pani obecną sytuację za lepszą niż przed rokiem?” określają preferencje na zbiorze zbiorów budżetowych odpowiadające niejawnej funkcji użyteczności.

Popyt Marshalla jest natomiast bardzo praktyczny – to, co wybieramy w konkretnych sytuacjach: to on właśnie, po zagregowaniu, jest zawarty w statystykach. Jeżeli jest funkcją, to określa jedyny możliwy wybór ze zbioru budżetowego.

Stwierdzenie 5.1

a) Jeśli konsument ma quasi-wklęsłą funkcje użyteczności, to odwzorowanie popytu $x$ ma wypukłe wartości, a jeśli ściśle quasi-wklęsłą, to odwzorowanie popytu $x$ jest funkcją;

b) Jeśli preferencje są lokalnie nienasycone, to odwzorowanie popytu spełnia prawo Walrasa: $\forall y\in x(\mathbf{p},m)$ zachodzi równość $\mathbf{p}^{{T}}y=m$ ;

c) Odwzorowanie popytu jest jednorodne stopnia $0$ ;

d) Jeśli funkcja użyteczności jest ciągła, to odwzorowanie popytu jest górnie półciągłe (jeśli jest funkcją, to jest to funkcja ciągła) i ma niepuste wartości.

Stwierdzenie 5.2

Własności niejawnej funkcji użyteczności $v$ .

a) Funkcja $v$ jest niemalejącą funkcją $m$ i nierosnącą $p_{{i}}$ , a jeśli preferencje są lokalnie nienasycone, to ponadto jest ścisle rosnącą funkcją $m$ ;

b) Funkcja $v$ jest jednorodna stopnia $0$ ;

c) Funkcja $v$ jest quasi-wypukła ze względu na $p$ ;

d) Jeśli funkcja użyteczności jest ciągła, to $v$ jest ciągła $.$

(obu stwierdzeń)

Punkty 5.1 a), b) i c) oraz 5.2 a) i b) są natychmiastowe. Pozostaje więc udowodnić pozostałe trzy.

5.2 c) Weźmy dowolne wektory cen $\mathbf{p}$ i $\mathbf{p}^{{\prime}}$ i $t\in(0,1)$ . Niech $\mathbf{p}^{{\prime\prime}}=t\mathbf{p}+(1-t)\mathbf{p}^{{\prime}}$ .

Łatwo pokazać, że zbiór $B_{{\mathbf{p}^{{\prime\prime}},m}}\subseteq B_{{\mathbf{p},m}}\cup B_{{\mathbf{p}^{{\prime}},m}}$ . Przypuśmy przeciwnie – czyli dla pewnego $x$ spełniającego $(\mathbf{p}^{{\prime\prime}})^{{T}}x\leq m$ zachodzi wówczas $\mathbf{p}^{{T}}x>m$ i $(\mathbf{p}^{{\prime}})^{{T}}x>m$ . Jeśli pomnożymy te nierówności przez $t$ i $(1-t)$ , odpowiednio i dodamy stronami, dostaniemy $(\mathbf{p}^{{\prime\prime}})^{{T}}x>m$ – sprzeczność.

Tak więc $v(\mathbf{p}^{{\prime\prime}},m)=\max _{{x\in B_{{\mathbf{p}^{{\prime\prime}},m}}}}u(x)\leq\max _{{x\in B_{{\mathbf{p},m}}\cup B_{{\mathbf{p}^{{\prime}},m}}}}u(x)=$ $=\max\left(\max _{{x\in B_{{\mathbf{p},m}}}}u(x),\max _{{x\in B_{{\mathbf{p}^{{\prime}},m}}}}u(x)\right)=\max(v(\mathbf{p},m),v(\mathbf{p}^{{\prime}},m))$ .

Własności 5.1 d) i 5.2 d) dowodzimy łącznie z twierdzenia o maksimum 4.1. Musimy pokazać ciągłość odwzorowania, oznaczmy je przez $\Gamma$ , które przyporządkowuje $(\mathbf{p},m)$ zbiór $B_{{\mathbf{p},m}}$ .

Górna półciągłość. Udowodnimy górną półciągłość z definicji.

Uwaga – ze względu na to, że przeciwobrazy górne nie zachowują się przy sumowaniu zbiorów, dowód ”epsilonowo-deltowy”, jakim zazwyczaj dowodzimy ciągłości funkcji, czyli dowodzenie, że przeciwobrazy pewnej bazy otoczeń są otwarte, nie wystarczy do udowodnienia półciągłości górnej odwzorowania.

Pełen dowód na wykładzie.

Dolna półciągłość. Ponieważ przeciwobrazy dolne zachowują się przy sumowaniu zbiorów, wystarczy ograniczyć się do bazy zbiorów otwartych – kul otwartych w pewnej normie na zbiorze $\mathbb{X}$ .

Pełen dowód na wykładzie.

∎

Ćwiczenie 5.1

Obliczyć niejawną funkcję użyteczności i odwzorowanie popytu dla $u(x_{1},x_{2})$ równej

a) $a_{1}\cdot x_{1}+a_{2}\cdot x_{2}$ przy $a_{i}>0$ (doskonałe substytuty);

b) $min\{ a_{1}\cdot x_{1},a_{2}\cdot x_{2}\}$ przy $a_{i}>0$ (dobra doskonale komplementarne);

c) $x_{1}^{{a_{1}}}\cdot x_{2}^{{a_{2}}}$ przy $a_{i}>0$ (użyteczność Cobba-Douglasa).

Wskazówka:

[Do punktu c)] Nie unikać używania mnożników Lagrange'a.

Do wyliczenia popytu można też (choć nie trzeba) użyć pomocniczo monotonicznej transformacji funkcji użyteczności.

Udowodnić dostateczność – można to zrobić na co najmniej trzy sposoby.

Ćwiczenie 5.2

Obliczyć popyt i niejawną funkcję użyteczności dla konsumenta o funkcji użyteczności (zwanej przez ekonomistów CES) $u(x_{1},x_{2})=(x_{1}^{{\rho}}+x_{2}^{{\rho}})^{{\frac{1}{\rho}}}$ .

Wskazówka:

Najpierw sprawdzić, dla jakiego $\rho$ te preferencje są wypukłe.

Stwierdzenie 5.3

(Tożsamość Roya)

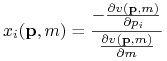Jeżeli spełnione są założenia modelu konsumenta, funkcja użyteczności jest różniczkowalna, odwzorowanie popytu $x$ jest funkcją różniczkowalną, $m>0$ , $p_{{i}}>0$ dla każdego $i$ oraz mnożnik Lagrange'a $\lambda(\mathbf{p},m)$ jest jednoznacznie wyznaczony i różny od $0$ , to jeśli dla każdego $i$ $x_{{i}}(\mathbf{p},m)>0$ , to $x_{{i}}(\mathbf{p},m)=\dfrac{-\frac{\partial v(\mathbf{p},m)}{\partial p_{{i}}}}{\frac{\partial v(\mathbf{p},m)}{\partial m}}$ .

Z twierdzenia o obwiedni pochodna funkcji maksimum po parametrze jest równa pochodnej lagrangianu po tym parametrze, a więc $\frac{\partial v(\mathbf{p},m)}{\partial p_{{i}}}=-\lambda(\mathbf{p},m)x_{{i}}(\mathbf{p},m)$ , a $\frac{\partial v(\mathbf{p},m)}{\partial m}=\lambda(\mathbf{p},m)$ .

∎

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.