8. Teoria wyboru konsumenta – funkcje popytu i ich własności – ciąg dalszy
8.1. Skompensowane prawo popytu
Konsekwencją słabego aksjomatu ujawnionych preferencji jest bardzo silny fakt, który ekonomiści nazywają skompensowanym prawem popytu. Mówi ono, że zmiana popytu jest ”przeciwna” do kierunku zmiany ceny, jeżeli rozważymy zmianę ceny skompensowaną zmianą dochodu, tak, aby uprzednio konsumowany koszyk był nadal na naszym ograniczeniu budżetowym.
Definicja 8.1
Skompensowane prawo popytu:
Dla każdego ![]() takich,
że
takich,
że ![]() zachodzi
nierówność
zachodzi
nierówność
![]() z ostrą
nierównością, jeśli
z ostrą
nierównością, jeśli ![]() .
.
Stwierdzenie 8.1
Jeżeli funkcja popytu ![]() jest jednorodna stopnia
jest jednorodna stopnia ![]() i spełnia prawo
Walrasa, to
i spełnia prawo
Walrasa, to ![]() spełnia słaby aksjomat ujawnionych preferencji wtedy i
tylko wtedy, gdy
spełnia słaby aksjomat ujawnionych preferencji wtedy i
tylko wtedy, gdy ![]() spełnia skompensowane prawo popytu.
spełnia skompensowane prawo popytu.
(![]() ) Jeśli
) Jeśli ![]() to, oczywiście,
to, oczywiście, ![]() .
.
W przeciwnym przypadku – ![]() mamy
mamy
![]() .
.
Ponieważ zmiana jest skompensowana, ![]() , a z prawa Walrasa wynika, że
, a z prawa Walrasa wynika, że ![]() . Stąd
. Stąd ![]() .
.
Z tego, że ![]() wynika, na mocy SAUP, że
wynika, na mocy SAUP, że ![]() . Stąd i z prawa Walrasa, na mocy którego
. Stąd i z prawa Walrasa, na mocy którego ![]() , wynika, że
, wynika, że ![]() .
.
(![]() ) Aby dowieść tej implikacji, potrzebujemy następującego Lematu.
) Aby dowieść tej implikacji, potrzebujemy następującego Lematu.
Lemat 8.1
Jeżeli funkcja popytu ![]() jest jednorodna stopnia
jest jednorodna stopnia ![]() i spełnia prawo
Walrasa, to słaby aksjomat ujawnionych preferencji jest rónoważny
słabemu aksjomatowi ujawnionych preferencji dla zmian skompensowanych
(i.e. tylko dla
i spełnia prawo
Walrasa, to słaby aksjomat ujawnionych preferencji jest rónoważny
słabemu aksjomatowi ujawnionych preferencji dla zmian skompensowanych
(i.e. tylko dla ![]() ).
).
Załóżmy teraz, że SAUP dla zmian skompensowanych nie zachodzi,
tzn. istnieje taki ![]() i
i
![]() , że
, że ![]() i
i ![]() .
.
Z prawa Walrasa mamy wówczas ![]() i
i ![]() , skąd
, skąd ![]() , co przeczy skompensowanemu prawu popytu – dla
, co przeczy skompensowanemu prawu popytu – dla ![]() powinniśmy uzyskać nierówność ostrą w przeciwną stronę.
powinniśmy uzyskać nierówność ostrą w przeciwną stronę.
Zauważmy, jakie są implikacje skompensowanego prawa popytu, jeśli rozważymy jedynie zmianę ceny jednego dobra: zmiana popytu na to dobro będzie przeciwna (już bez cudzysłowu) do kierunku zmiany ceny skompensowanej odpowiednim wzrostem dochodu, czyli, jak należało się spodziewać, przy skompensowanym wzroście ceny, o ile nasz popyt na to dobro się zmieni, to spadnie.
8.2. Równanie Słuckiego i jego konsekwencje
Teraz będziemy analizować efekty zmiany ceny, które już nie są skompensowane zmianą dochodu. W tej sytuacji już wiemy, że kierunek zmiany popytu nie musi być przeciwny do kierunku zmiany ceny np. w przypadku dóbr Giffena. Będziemy starali się rozłożyć zmianę popytu na skutek zmiany ceny na dwa efekty: jeden związany z samą zmianą stosunku cen, przy czym zmianę tę w jakiś sposób będziemy kompensować (tzw. efekt substytucyjny) i drugi związany ze zmianą siły nabywczej naszego dochodu (efekt dochodowy). Ten rozkład będziemy nazywać równaniem Słuckiego albo dekompozycją Słuckiego. W przypadku ciągłym ma on postać:
Twierdzenie 8.1 (Ciągłe równanie Słuckiego)
Jeżeli funkcje popytu ![]() i
i ![]() są funkcjami
różniczkowalnymi, mają wszystkie współrzędne dodatnie
dla dodatniego dochodu i wywodzą się od monotonicznych, lokalnie
nienasyconych preferencji o różniczkowalnej funkcji
użyteczności i mnożnik Lagrange'a jest wyznaczony jednoznacznie,
to
są funkcjami
różniczkowalnymi, mają wszystkie współrzędne dodatnie
dla dodatniego dochodu i wywodzą się od monotonicznych, lokalnie
nienasyconych preferencji o różniczkowalnej funkcji
użyteczności i mnożnik Lagrange'a jest wyznaczony jednoznacznie,
to
![]() .
.
Korzystamy z warunku dualności (stwierdzenie 6.6) ![]() dla
dla ![]() (czyli
(czyli ![]() ).
).
Różniczkujemy ten warunek obustronnie po ![]() . Otrzymujemy
. Otrzymujemy
![]() . Z lematu Shepharda (6.4)
. Z lematu Shepharda (6.4) ![]() z dualności. Podstawienie
z dualności. Podstawienie ![]() za
za ![]() i
i ![]() za
za ![]() i przeniesienie
i przeniesienie ![]() kończy dowód.
kończy dowód.
Ćwiczenie 8.1
Rozłożyć zmianę popytu dla preferencji Cobba-Douglasa na efekty dochodowy i substytucyjny, używając ciągłego równania Słuckiego.
Ćwiczenie 8.2
Udowodnić, że efekty substytucyjny i dochodowy z ciągłego równania Słuckiego są niezależne od wyboru konkretnej funkcji użyteczności odzwierciedlającej dane preferencje (choć odzwzorowanie popytu Hicksa jest od tego wyboru zależne).
Wniosek 8.1
Jeżeli funkcje popytu ![]() i
i ![]() są różniczkowalne, mają
wszystkie współrzędne dodatnie dla dodatniego dochodu i wywodzą
się od preferencji o różniczkowalnej funkcji
użyteczności, to macierz substytucji zdefiniowana jako
są różniczkowalne, mają
wszystkie współrzędne dodatnie dla dodatniego dochodu i wywodzą
się od preferencji o różniczkowalnej funkcji
użyteczności, to macierz substytucji zdefiniowana jako ![]() jest symetryczna, niedodatnio określona.
jest symetryczna, niedodatnio określona.
Pierwszą z wielkości występujących po prawej stronie równania Słuckiego nazywamy efektem substytucyjnym, drugą efektem dochodowym.
Jeżeli rozważamy efekt zmiany ceny tylko jednego dobra, to efekt
substytucyjny jest zawsze przeciwny do kierunku zmiany ceny, ponieważ
macierz ![]() jest niedodatnio określona, i nie może
być zerowy, jeśli zakładamy różniczkowalność
funkcji użyteczności. Natomiast znak efektu dochodowego zależy
od tego, czy jest to dobro normalne czy podrzędne. W przypadku dobra
podrzędnego o silnym efekcie dochodowym, dodatni efekt dochodowy
może przezwyciężyć ujemny efekt substytucyjny, jak w
przypadku dóbr Giffena.
jest niedodatnio określona, i nie może
być zerowy, jeśli zakładamy różniczkowalność
funkcji użyteczności. Natomiast znak efektu dochodowego zależy
od tego, czy jest to dobro normalne czy podrzędne. W przypadku dobra
podrzędnego o silnym efekcie dochodowym, dodatni efekt dochodowy
może przezwyciężyć ujemny efekt substytucyjny, jak w
przypadku dóbr Giffena.
Oczywiście ciągłą postać równania Słuckiego
poprzedziła wersja dyskretna, a nawet dwie wersje, matematycznie
trywialne. Jeśli interesować będzie nas wartość
przybliżona zmiany popytu na skutek zmiany ceny z ![]() na
na ![]() , możemy skorzystać z równania Słuckiego:
, możemy skorzystać z równania Słuckiego:
![]() .
.
Wbrew temu, czego należałoby się spodziewać, dyskretne równanie Słuckiego nie jest dokładną wersją tego przybliżenia; dopiero wprowadzone później równanie Hicksa. Dyskretne równanie Słuckiego wynika z następującego spostrzeżenia.
Uwaga 8.1
![]() .
.
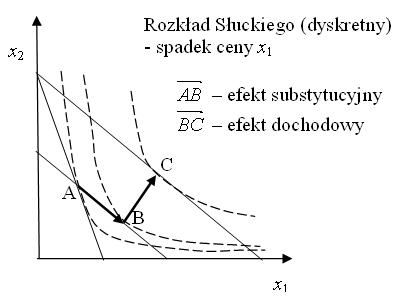
Definicja 8.2
Jeśli ![]() to powyższą tożsamość nazywamy dyskretnym równaniem Słuckiego,
to powyższą tożsamość nazywamy dyskretnym równaniem Słuckiego, ![]() to efekt dochodowy,
a
to efekt dochodowy,
a ![]() – efekt substytucyjny.
– efekt substytucyjny.
Ćwiczenie 8.3
Rozpisać efekty substytucyjny i dochodowy Słuckiego dla obu dóbr w przypadku wzrostu ceny ![]() przy niezmienionej cenie
przy niezmienionej cenie ![]() dla:
dla:
a) funkcji użyteczności Cobba-Douglasa o ![]() ;
;
b) dóbr doskonale komplementarnych;
c) doskonałych substytutów, w przypadku gdy przed zmianą konsumowane było jedynie dobro 1 i
(i) po zmianie nadal konsumowane jest dobro 1;
(ii) po zmianie konsumowane jest tylko dobro 2.
Dyskretny odpowiednik ciągłego równania Słuckiego wynika z następującego spostrzeżenia.
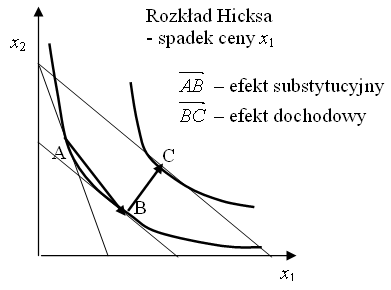
Uwaga 8.2
![]() .
.
Definicja 8.3
Powyższą tożsamość nazywamy równaniem Hicksa,
![]() to efekt dochodowy Hicksa, a
to efekt dochodowy Hicksa, a ![]() – efekt substytucyjny Hicksa.
– efekt substytucyjny Hicksa.
Ćwiczenie 8.4
Rozpisać efekty substytucyjny i dochodowy Hicksa dla obu dóbr w przypadku wzrostu ceny ![]() przy niezmienionej cenie
przy niezmienionej cenie ![]() dla:
dla:
a) funkcji użyteczności Cobba-Douglasa o ![]() ;
;
b) dóbr doskonale komplementarnych;
c) doskonałych substytutów, w przypadku gdy przed zmianą konsumowane było jedynie dobro 1 i
(i) po zmianie nadal konsumowane jest dobro 1;
(ii) po zmianie konsumowane jest tylko dobro 2.
Interpretacja obu dyskretnych rozkładów wektora zmiany popytu na sumę dwóch wektorów jest taka sama: efekt zmiany ceny rozkładamy na efekt substytucyjny, mający jedynie odzwierciedlać reakcję na zmianę stosunku cen i zaniedbywać skutki zmiany siły nabywczej, i efekt dochodowy wynikający ze zmiany siły nabywczej dochodu. Efekt substytucyjny, to w każdym wypadku zmiana popytu spowodowana zmianą ceny skompensowaną taką zmianą dochodu, aby nie zmieniła się siła nabywcza dochodu, a efekt dochodowy to różnica zmiany popytu i efektu substytucyjnego. Niejednoznaczność wynika z niejasnej interpretacji terminu ”siła nabywcza”: równanie Hicksa gwaranuje, że nie zmienia się sytuacja konsumenta (jest tak samo dobra), a równanie Sluckiego jedynie że uprzednio wybrany koszyk znajduje się nadal na ograniczeniu budżetowym konsumenta (na skutek dodania lub odjęcia ”na papierze” dochodu). Oczywiście efekty Słuckiego łatwiej wyliczyć – nie musimy odwoływać się do nieobserwowalnej funkcji popytu Hicksa.
Podobnie jak w przypadku ciągłego równania Słuckiego, efekty substytucyjne są zawsze ujemne, a znak efektu dochodowego zależy od tego, czy dobro jest normalne czy podrzędne.
Ćwiczenie 8.5
Udowodnić, że efekty substytucyjny i dochodowy z rozkładu Słuckiego (dyskretnego) i rozkładu Hicksa są niezależne od wyboru konkretnej funkcji użyteczności odzwierciedlającej dane preferencje.
Ćwiczenie 8.6
Która z krzywych jest bardziej elastyczna cenowo, tzn. silniej reaguje spadkiem popytu na wzrost ceny (czyli ma większą co do modułu elastyczność cenową). Rozważamy tylko sytuację, gdy nie występuje efekt Giffena.
Skorzystać z ciągłego równania Słuckiego.