Zagadnienia
2. Mechanika statystyczna
2.1. Dlaczego żelazo jest magnesem?
Jeżeli magnes wykonany z żelaza podgrzejemy powyżej 770 stopni Celsjusza, tak-zwanej temperatury Curie,
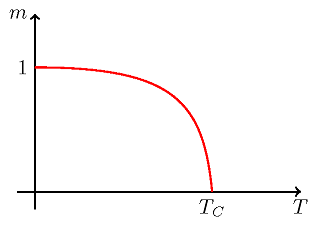
to straci on zdolności magnetyczne. Wykres namagnesowania jako funkcja temperatury
Zjawisko te stara się wyjaśnić teoria ciała stałego, dział fizyki zajmujący się własnościami ciał makroskopowych. W bardzo dużym uproszczeniu przyjmujemy, że namagnesowanie sztabki żelaza jest sumą wektorową małych magnesów związanych z poszczególnymi atomami żelaza. Z jednej strony, siły oddziaływań pomiędzy magnesikami prowadzą do ich ułożenia wzdłuż jednego kierunku. Z drugiej strony, ruchy cieplne atomów zaburzają ten idealny porządek. Wynikiem tej rywalizacji pomiędzy czynnikiem energetycznym a czynnikiem losowym rosnącym w miarę wzrostu temperatury ciała są jego własności makroskopowe. Działem fizyki zajmującym się wyprowadzaniem własności makroskopowych ciał z mikroskopowych oddziaływań pomiędzy ich elementarnymi składnikami, atomami lub cząsteczkami, jest fizyka statystyczna.
2.2. Magnes matematyczny - Model Isinga
W modelu Isinga, oddziałujące obiekty - magnesiki - umieszczone są w węzłach kraty
| (2.1) |
Przyjmujemy, że oddziałują ze sobą spiny, które są najbliższymi sąsiadami.
| (2.2) |
gdzie
Hamiltonian w mechanice klasycznej oddziałujących cząstek jest sumą energii kinetycznej poszczególnych cząstek i energii potencjalnej oddziaływań między nimi (patrz wykład Wojtyńskiego). W powyższym wyrażeniu nie uwzględniamy energii potencjalnej.
Nasz układ spinowy podlega nieustannym ruchom cieplnym i w związku z tym jest układem stochastycznym.
Powinniśmy więc określić prawdopodobieństwa przebywania układu w każdym z mikroskopowych stanów
czyli elementów zbioru
| (2.3) |
Wprowadzamy następujący rozkład prawdopodobieństwa,
| (2.4) |
gdzie
| (2.5) |
jest czynnikiem normalizującym prawdopodobieństwo. W fizyce
Niezwykle ważną wielkością w fizyce jest energia swobodna, zwana także potencjałem termodynamicznym,
| (2.6) |
Wartości oczekiwane zmiennych losowych możemy dostać różniczkując potencjał. W szczególności łatwo zobaczyć, że
| (2.7) |
Ćwiczenie 2.1
Udowodnij powyższą równość.
Ćwiczenie 2.2
Udowodnij, że
2.2.1. Metoda konturów Peierlsa
Będziemy rozważać układy z plusowymi albo minusowymi warunkami brzegowymi w dwuwymiarowym modelu Isinga,
Zbiory konfiguracji
| (2.8) |
Wtedy odpowiedni wielki kanoniczny rozkład prawdopodobieństwa ma następującą postać,
| (2.9) |
Przyjmijmy dla uproszczenia, że
gdzie poprzez zbieżność rozumiemy słabą zbieżność z gwiazdką miar na
Twierdzenie 2.1
Oznacza to, że choć brzegu już nie ma, pozostał jego ślad. Hamiltonian w granicy termodynamicznej dla
Twierdzenie 2.2
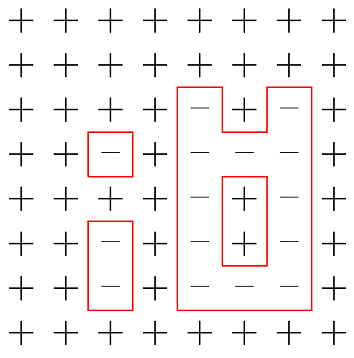
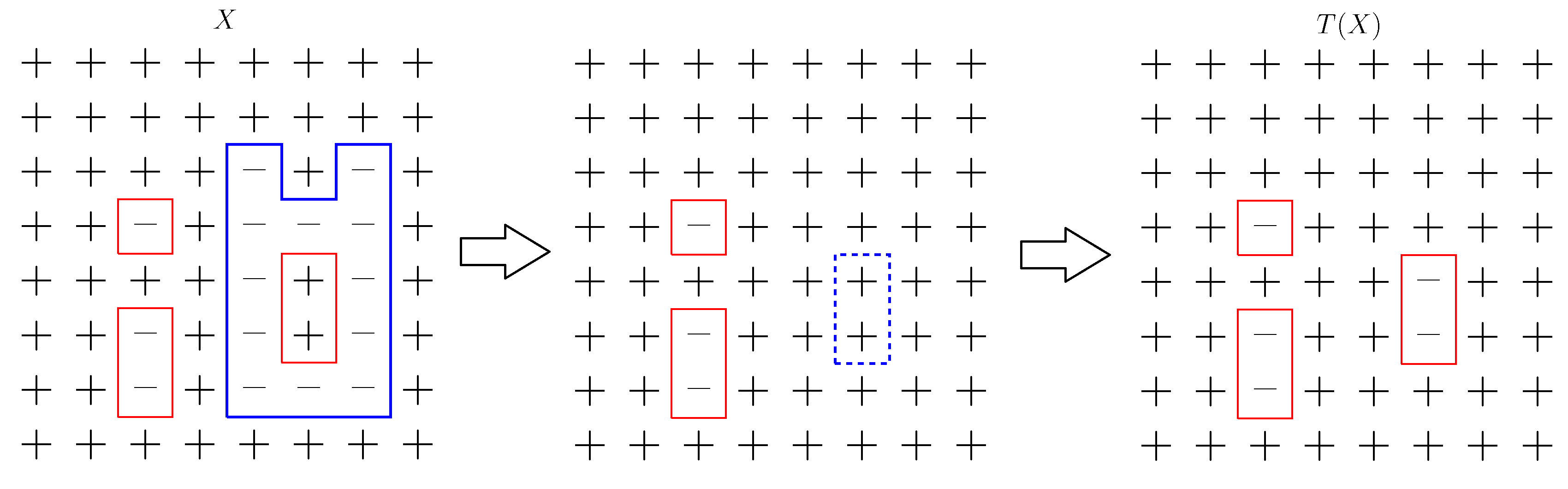
Wprowadzimy teraz pojęcie konturu konfiguracji.
Dla każdej pary sąsiadów
Formalnie,
Konturem
Definiujemy
Dowód Twierdzenia 2
| (2.10) |
gdzie sumowanie jest po konturach otaczających
| (2.11) |
Ostatecznie mamy
| (2.12) |
gdzie
W analogiczny sposób dla minusowych warunków brzegowych otrzymujemy
i
Natomiast przy obniżaniu temperatury, w temperaturze Curie mamy do czynienia z przejściem fazowym drugiego rodzaju. Jest to przejście fazowe typu ciągłego - namagnesowanie w sposób ciągły wzrasta od zera przy podwyższaniu temperatury powyżej punktu Curie, patrz Rys. 2.1.
2.2.2. Jednowymiarowy model Isinga
2.3. Klasyczne gazy sieciowe
W rozdziale tym uogólnimy klasyczny model Isinga na przypadek więcej niż dwóch możliwych stanów, w których może znajdować się każdy
wierzchołek sieci, na oddziaływania o większym zasięgu i niekoniecznie dwucząstkowe. Nasze modele będziemy interpretować
w języku gazów sieciowych. W modelu gazu sieciowego w każdym wierzchołku sieci
Przez potencjał
Definicja 2.1
Definicja 2.2
Widzimy więc, że model Isinga zadany jest przez potencjał dwucząstkowy o zasięgu
Definicja 2.3
Hamiltonianem w skończonej objętości
Definicja 2.4
Konfiguracja
Podstawowym pojęciem w mechanice statystycznej oddziałujących cząstek jest stan podstawowy. Intuicyjnie są to konfiguracje o najmniejszej energii. Energia nieskończonej konfiguracji zazwyczaj bywa nieskończona. Tak więc intuicyjna definicja nie ma sensu. Zamiast energii rozważmy w takim razie gęstość energii
Definicja 2.5
Chcielibyśmy zdefiniować konfiguracje stanu podstawowego jako te, które minimalizują gęstość energii.
Uwolniliśmy się od nieskończonych energii ale mamy inny kłopot. Jeśli
Definicja 2.6
Dla lokalnego wzbudzenia
Definicja 2.7
Powyższa definicja ma charakter lokalny. Konfiguracja stanu podstawowego jest taką konfiguracją, której nie można lokalnie zaburzyć tak aby zmniejszyć wartość Hamiltonianu względnego. Zastanowimy się teraz w jakim sensie konfiguracje stanu podstawowego posiadają własność globalnego minimum energii.
Twierdzenie 2.3
Jeśli
Ćwiczenie 2.3
Udowodnij powyższe twierdzenie.
Odwrotna implikacja nie jest oczywiście prawdziwa. Twierdzenie odwrotne zachodzi natomiast jeżeli będziemy rozważać tylko konfiguracje okresowe.
Definicja 2.8
Mamy następującą postać twierdzenia odwrotnego.
Twierdzenie 2.4
Ćwiczenie 2.4
Znajdź wszystkie konfiguracje stanu podstawowego dwuwymiarowego ferromagnetycznego modelu Isinga.
Twierdzenie 2.5
Dla każdego translacyjnie niezmienniczego potencjału skończenie zasięgowego, zbiór konfiguracji stanu podstawowego jest niepusty.
Ćwiczenie 2.5
Udowodnij powyższe twierdzenie.
Skorzystaj z tego, że
2.4. Kwazikryształy
Rozpoczniemy od fundamentalnego pytania: czy każdy skończenie zasięgowy translacyjnie niezmienniczy potencjał posiada co najmniej jedną okresową konfigurację stanu podstawowego?
Poniżej zamieszczamy krótki szkic rozumowania zamieszczonego w książce P.W. Andersona ….. i mającego odpowiadać twierdząco na powyższe pytanie.
Ćwiczenie 2.6
Znajdź błąd w powyższym rozumowaniu.
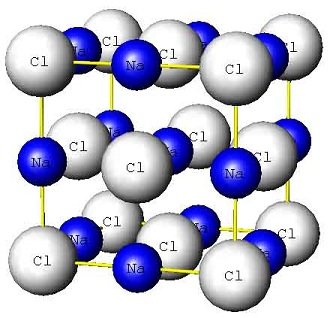
W tym samym 1984 roku odkryto kwazikryształy, których atomy rozmieszczone są w przestrzeni w sposób nieokresowy []. Był to pierwszy eksperymentalny kontrprzykład do ogólnie przyjętej hipotezy, że ciało stałe przy odpowiednio niskich temperaturach zawsze powinno występować w formie krystalicznej czyli przestrzennie okresowej. Typowym przykładem są kryształki soli kamiennej NaCL, w których atomy sodu i chloru tworzą okresową strukturę przedstawioną na Rys. 2.5.
Ćwiczenie 2.7
Udowodnij, że każdy jednowymiarowy translacyjnie-niezmienniczy skończenie-zasięgowy potencjał gazu sieciowego posiada co najmniej jedną okresową konfigurację stanu podstawowego.
Każda jednowymiarowa konfiguracja może być przedstawiona jako nieskończona droga na pewnym grafie
2.5. Nieokresowe mozaiki - krótka historia rekordu świata
W rozdziale tym będziemy rozważać pokrycia płaszczyzny wielobokami nazywanymi przez nas kafelkami lub dachówkami. Wybieramy skończoną liczbę kafelków, nazywamy je prototypami. Mamy do dyspozycji nieskończoną liczbę kopii każdego prototypu. Staramy się pokryć nimi nieskończoną płaszczyznę tak aby każdy punkt płaszczyzny został pokryty i żeby kafelki nie miały części wspólnych (z wyjątkiem brzegów).
W 1900 roku David Hilbert zaprezentował 23 fundamentalne problemy matematyczne. Druga cześć 18-tego problemu zawiera w istocie następujące (nadal pozostawione bez odpowiedzi) pytanie: Czy istnieje wielobok pokrywający nieskończoną płaszczyznę tylko w sposób nieokresowy?
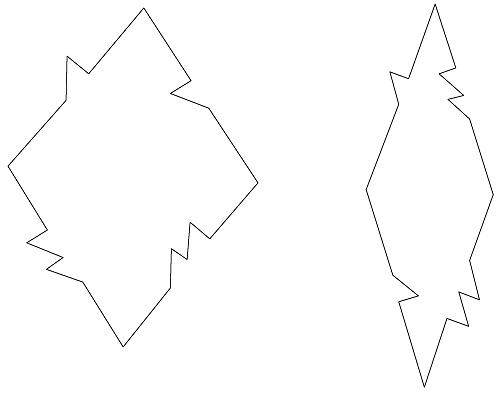
W 1974 roku, na długo przed odkryciem kwazikryształów, Roger Penrose, fizyk matematyczny z Oxfordu, skonstruował (albo odkrył jak kto woli) dwie dachówki, zwane latawcem i grotem, którymi można pokryć płaszczyznę tylko w sposób nieokresowy, Rys. 2.6 (patrz artykuł w delcie i Scientific American).
W dalszej części tego rozdziału będziemy zajmować się dachówkami kwadratowymi z wcięciami i wypustkami na bokach.
Wcięcia i wypustki możemy reprezentować odpowiednimi kolorami boków. Dwa sąsiednie kwadraty pasują do siebie gdy wypustki jednego pasują
do wcięć drugiego albo alternatywnie kolory odpowiednich boków są takie same. Dachówki takie nazywane są dominami albo dachówkami Wanga.
Jeżeli można nimi pokryć płaszczyznę, to ich środki tworzą regularny graf
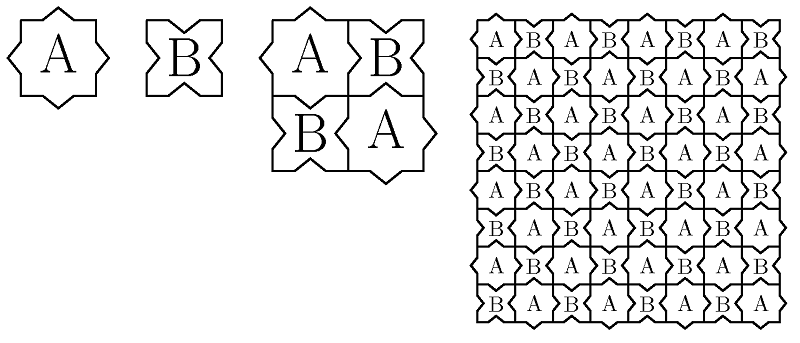
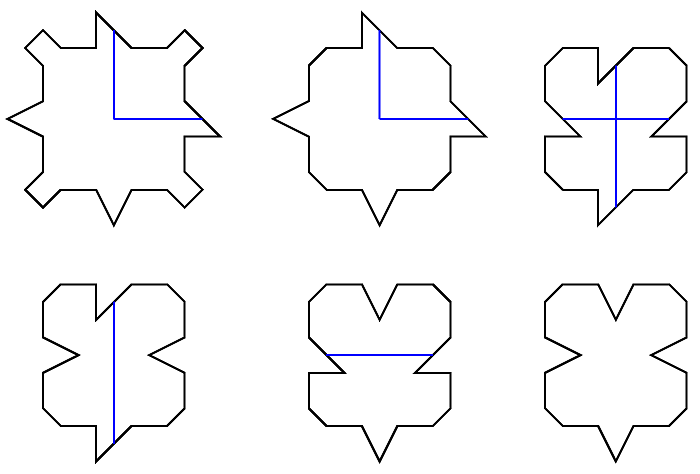
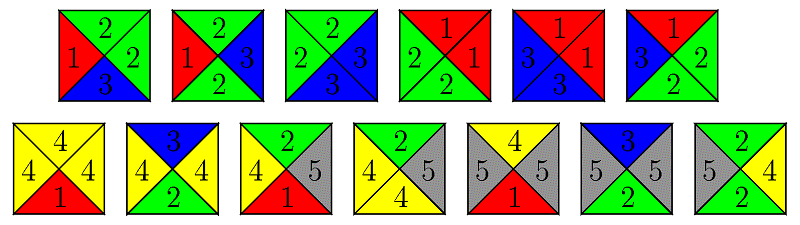
W 1961 roku Hao Wang postawił hipotezę, że każdy skończony zestaw płytek domina pokrywający płaszczyznę może pokryć ją także w sposób okresowy. Hipoteza ta miała związek z problem rozstrzygalności - czy istnieje uniwersalny program komputerowy (maszyna Turinga), który w skończonej liczbie kroków dostarczyłby odpowiedzi na pytanie czy dany zestaw domin może pokryć płaszczyznę. Jeżeli powyższa hipoteza byłaby prawdziwa, to próbując stopniowo pokrywać coraz większe obszary płaszczyzny odkrylibyśmy w skończonej liczbie kroków układ domin, który moglibyśmy powtarzać i skonstruować w ten sposób pokrycie okresowe. Pierwszy kontrprzykład pojawił się w 1996 roku i jest autorstwa Roberta Bergera []. Zaprojektował on 20426 kafelków pokrywających płaszczyznę tylko w sposób nieokresowy. W 1971 roku Raphael Robinson obniżył liczbę dachówek o tej własności do 56 []. Na Rys. 2.8 zaprezentowanych jest 6 dachówek Robinsona, pozostałe można z nich otrzymać przy pomocy obrotów i odbić.
Na Rys. 2.9 pokazana jest struktura nieokresowej mozaiki Robinsona.
W 1977 Robert Ammann ustanowił nowy rekord świata minimalnej liczby kafelków pokrywających płaszczyznę tylko w sposób nieokresowy. Następnym rekordzistą został w 1996 roku Jarrko Kari z 14 kafelkami) []. Obecny rekord 13 kafelków, też z 1996 roku, należy do Karela Culika II [], Rys. 2.10.
Zapraszam do pobicia rekordu świata.
2.6. Mikroskopowy model kwazikryształu
Zaprezentujemy teraz translacyjnie niezmienniczy skończenie zasięgowy potencjał gazu sieciowego nieposiadający żadnej okresowej
konfiguracji stanu podstawowego. Nasza konstrukcja opiera się na nieokresowych mozaikach. Przykładowo użyjemy dachówek Ammanna.
Każdą dachówkę na Rys. X traktujemy jako rodzaj cząstki. Zbiorem konfiguracji gazu sieciowego jest więc
Fundamentalnym pytaniem jest czy nieokresowa struktura obecna w konfiguracjach stanu podstawowego, czyli w zerowej temperaturze, przetrwa w dodatniej temperaturze. Innymi słowy czy struktura nieokresowa jest odporna na dowolnie małe cieplne fluktuacje.
Czy istnieje klasyczny model gazu sieciowego z translacyjnie niezmienniczym skończenie zasięgowym potencjałem bez okresowych konfiguracji stanów podstawowych i z nieokresowym stanem Gibbsa?
Rozważmy model gazu sieciowego odpowiadający dachówkom Ammanna. Niech Y będzie jedną z nieokresowych konfiguracji stanu podstawowego,
Czy dla każdego
Odpowiedź twierdząca na powyższe pytanie pociąga za sobą nieokresowość
Modele gazów sieciowych odpowiadające dachówkom Robinsona badane były w [].
2.6.1. Dodatek 2
Zbiór wszystkich konfiguracji gazu sieciowego z
jest zbiorem nieprzeliczalnym.
Aby rozważać miary na tym zbiorze musimy wprowadzić
wprowadzamy topologię produktową
czyli najmniejsza topologię, w której projekcje
Ćwiczenie 2.8
Scharakteryzuj zbiory otwarte w powyższej topologii produktowej.
Ćwiczenie 2.9
Scharakteryzuj zbieżność ciągów w
Okazuje się, że wszystkie nieokresowe mozaiki przedstawione w poprzednim rozdziale, a co za tym idzie nieokresowe konfiguracje
stanu podstawowego w odpowiednim modelu gazu sieciowego, mają następującą własność. Niech
Chcielibyśmy aby istniała stała
| (2.13) |
.
Okazuje się jednak, że we wszystkich przykładach mamy
Czy istnieje skończony zbiór typów dachówek, pokrywający płaszczyznę tylko w sposób nieokresowy z jedyną translacyjnie niezmiennicza miarą