Rozpatrzmy modelowe zadanie jednowymiarowe (7.1) z zerowymi warunkami brzegowymi i c=0, którego rozwiązanie oznaczymy u*.

Następnie weźmy dowolną funkcję ciągłą ϕ, która jest kawałkami C1 na odcinku, tzn. która ma ciągłą pochodną poza skończoną ilością punktów taką, że ϕ⁢a=ϕ⁢b=0. Przemnóżmy równanie L⁢u=f przez tę funkcję. Ze wzoru na całkowanie przez części otrzymujemy:

Oczywiście tutaj d⁢ϕd⁢x jest zdefiniowana poza skończoną ilością punktów nieciągłości.

Zamiast zadania (7.1) możemy rozpatrzyć zadanie znalezienia funkcji u* w odpowiedniej przestrzeni V funkcji określonych na odcinku a,b zawierających funkcje kawałkami C1 i zerujące się w końcach odcinka (na razie nie ustalajmy precyzyjnie o jaką przestrzeń chodzi) takiej, żeby

Oczywiście rozwiązanie (7.1) spełnia (11.1), a przy odpowiednim doborze V (oraz dostatecznej gładkości f) można pokazać, że rozwiązanie (11.1) również spełnia (7.1). Zadanie (11.1) nazywamy sformułowaniem uogólnionym (słabym, wariacyjnym) zadania (7.1). Zaś (7.1) nazywamy sformułowaniem klasycznym. Metoda elementu skończonego, która jest szczególnym przypadkiem metody Galerkina polega na tym, że wprowadzamy w specjalny sposób skończenie wymiarową podprzestrzeń przestrzeni V. Następnie szukamy rozwiązania w tej przestrzeni dyskretnej, które spełnia zadanie wariacyjne (11.1) z tym, że przestrzeń V jest zastąpiona przez naszą dyskretną podprzestrzeń.

Proszę zauważyć, że podejście wariacyjne jest inne od metody różnic skończonych, w której konstrukcja rozwiązania określonego na zbiorze dyskretnym (siatce) polega na zastąpieniu odpowiednich pochodnych w równaniu różniczkowym odpowiednimi ilorazami różnicowymi na tej siatce.

Wprowadźmy podział (triangulacje) odcinka a,b na pododcinki (elementy) Th⁢a,b=τk, gdzie τk=xk,xk+1 dla a=x0<…<xN-1<xN=b. Za parametr tego podziału przyjmijmy h=maxk⁡xk-xk-1, a punkty xk nazwiemy punktami nodalnymi (węzłami) tego podziału.

Oczywiście najprostszym podziałem jest podział równomierny, jeśli bierzemy xk=k*h dla h=b-a/N.

Zakładamy, że rozpatrujemy rodzinę podziałów z h dążącym do zera.

Teraz na bazie danego podziału Th⁢a,b możemy wprowadzić przestrzeń dyskretną:

gdzie P1=s⁢p⁢a⁢n⁢1,x jest przestrzenią wielomianów liniowych, tzn. stopnia nie większego niż jeden. Funkcje z tej przestrzeni to funkcje kawałkami liniowe (czyli klasyczne splajny liniowe) z zerowymi warunkami brzegowymi na brzegu, czyli w szczególności są to funkcje ciągłe kawałkami klasy C1, zatem Vh⊂V.

Zadanie dyskretne polega na znalezieniu uh∈Vh takiego, że

Pozostawimy jako zadanie wykazanie istnienia jednoznacznego rozwiązania (11.2).

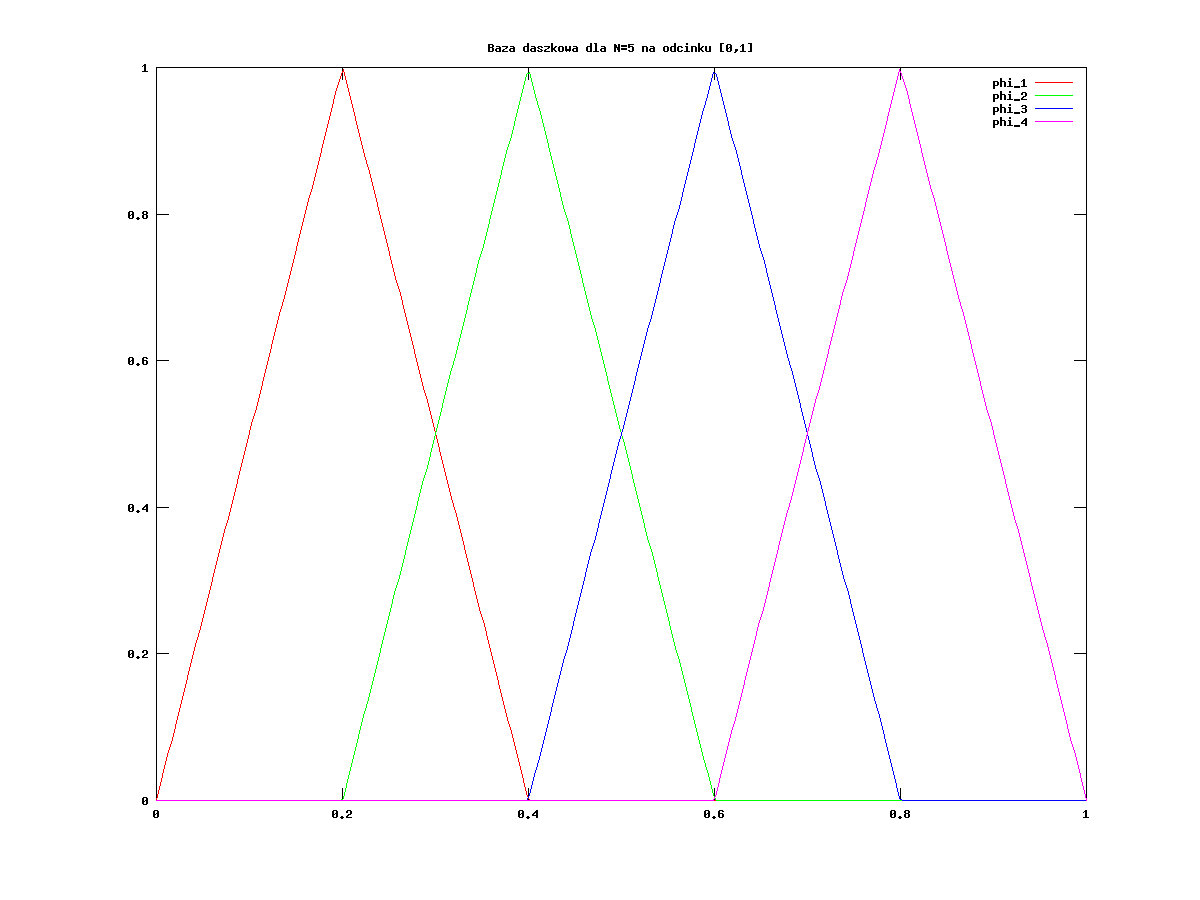
Na razie wprowadźmy tzw. funkcję nodalną: niech ϕk∈Vh dla k∈1,…,N-1 będzie taką funkcją, że ϕk⁢xk=1 i ϕk⁢xj=0 dla j≠k. Możemy podać wzór na taką funkcję:

Widzimy wykres kilku takich funkcji, por. rysunek 11.1.

Nietrudno pokazać, że ϕk jest elementem Vh, i że ϕ1,…,ϕN-1 tworzy bazę Vh taką, że jeśli u∈Vh, to

gdzie u⁢xk wartość funkcji u w punkcie nodalnym xk. Wstawiając uh=∑k=1N-1uh⁢xk⁢ϕk do (11.2) otrzymujemy następujący układ równań liniowych:

z u→=u⁢x1,…,u⁢xN-1T,

dla fk=∫abf⁢ϕk⁢⁢d⁢x.

Zauważmy, że macierz Ah jest symetryczna i trójdiagonalna. Można wykazać, że jest dodatnio określona, więc można powyższy układ rozwiązać metodą przeganiania lub odpowiednim wariantem metody Choleskiego kosztem rzędu c*N dla stałej c niezależnej od N.

Zastanówmy się nad zbieżnością uh do rozwiązania u*. Najpierw trzeba ustalić w jakiej normie chcemy wykazać zbieżność.

Naturalną normą jest norma energetyczna związana z formą dwuliniową w słabym sformułowaniu (11.1):

Wprowadzając oznaczenie eh=u*-uh i odejmując (11.2) od (11.1) otrzymujemy:

Następnie dla dowolnego vh∈Vh widzimy, że

Korzystając z nierówności Schwarza w L2⁢a,b otrzymujemy:

czyli

Przyjmując za vh liniowy interpolator u* w punktach nodalnych, tzn. Ih⁢u*:=∑ku*⁢xk⁢ϕk, można wykazać:

dla pewnych stałych Ck niezależnych od h, u* i a,b. Dowód tego oszacowania pozostawiamy jako zadanie, wynika on wprost z oszacowań błędu interpolacji dla splajnów liniowych.

Wtedy od razu otrzymujemy:

czyli dla funkcji klasy C2 błąd w normie energetycznej zachowuje się jak O⁢h.

Można też wykazać, że w normie L2⁢a,b zachodzi:

czyli błąd zachowuje się jako O⁢h2 - co nie jest oczywiste.

Porównajmy to oszacowanie z oszacowaniem błędu z metody różnic skończonych (MRS) na siatce równomiernej dla tego samego zadania różniczkowego. Można pokazać wtedy zbieżność dyskretną O⁢h2 w dyskretnej normie Lh2, por. (10.4), która w przybliżeniu odpowiada normie L2, czyli możemy powiedzieć, że szybkość zbieżności w tym przypadku metody elementu skończonego i metody różnic skończonych jest tego samego rzędu. Ale w MRS musieliśmy założyć równomierność siatki i wyższą gładkość rozwiązania (u*∈C4⁢a,b).

Przestrzeń dyskretną Vh można też zdefiniować inaczej.

Dla danego podziału Th⁢a,b zdefiniujemy następujące przestrzenie elementu skończonego dla dowolnego p=1,2,3,4,…:

gdzie Pp jest przestrzenią wielomianów stopnia nie przekraczającego p.

Widzimy, że Vh=V1h. Przestrzeń V2h nazywamy przestrzenią elementu skończonego funkcji ciągłych kawałkami kwadratowych, a przestrzeń V3h - przestrzenią elementu skończonego funkcji ciągłych kawałkami kubicznych, czy inaczej - metodą elementu skończonego typu Lagrange'a kwadratową lub kubiczną. Możemy teraz postawić zadanie dyskretne, jak poprzednio, tzn. szukamy uh,p∈Vph takiego, że

Zadanie to ma jednoznaczne rozwiązanie. Analogicznie jak dla elementu liniowego możemy wprowadzić tu tzw. bazę nodalną w Vph. Wprowadzamy dodatkowe punkty wewnątrz odcinka xk,xk+1 dla k=0,…,N-1:

Oczywiście xk,0=xk.

Dla każdego punktu xk,j oprócz x0,0=x0=a wprowadzamy funkcję bazową ϕk,j∈Vph taką, że

Można pokazać, że ϕk,jk,j jest bazą i to taką, że

Powstaje pytanie: po co stosować przestrzenie Vph dla p>1?

Jeśli rozwiązanie u* jest bardziej regularne, tzn. należy do Cp+1⁢a,b, to można wykazać, że dla Ih,p=∑k,ju⁢xk,j⁢ϕk,j∈Vph:

i stąd, jak poprzednio dla elementu liniowego, otrzymujemy, że

czyli błąd zachowuje się jak O⁢hp co oznacza, że w tej normie zachodzi zbieżność rzędu p.