Zagadnienia
3. Funkcja odwrotna
W analizie pewnego modelu dotyczącego transportu morfogenów w tkankach [16] istotną rolę odgrywa funkcja
a ściślej: funkcja odwrotna do niej,
Jasne jest, że wszelkie nasze komputerowe działania musimy zacząć od zdefiniowania funkcji
function v = sigmafun(s,M) v = (2/(M-1))*(1-(1-s).^(M-1)) - s.*(1-s).^(M-1); end
(Dalsze rozważania będziemy prowadzić dla
a to jest przecież ,,to samo”, co zbiór
Wobec tego wystarczy skorzystać z funkcji plot, ale ,,na opak”:
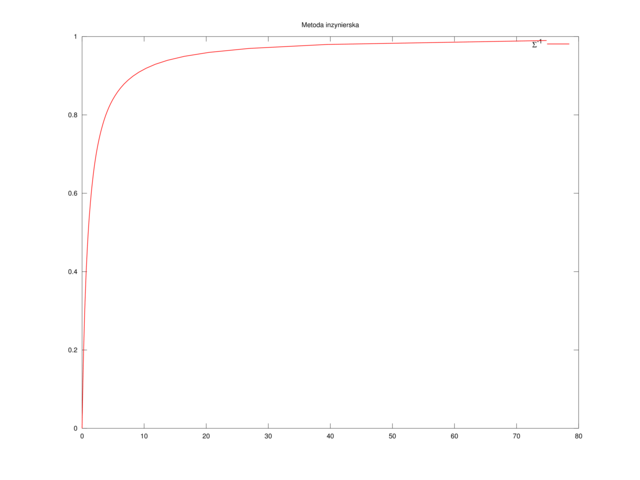
M = 0.5; s = linspace(0,1); plot(sigmafun(s,M), s, 'r-', 'linewidth', 2);
Z wykresu na rysunku 3.1 widzimy, że plot, znacznie bardziej wyraziste semilogy(sigmafun(s,M), 1-s). Jednak dla ustalenia uwagi, w dalszym ciągu pozostaniemy przy wykresie w skali liniowej.
3.1. Doprecyzowanie zadania
Niepokojący jest prawy koniec wykresu: wszak
Napiszemy zatem w Octave funkcję, która będzie wyznaczać wartości funkcji odwrotnej do
Aby dla zadanego fzero. Powyższą ideę implementuje funkcja sigmainv z poniższego listingu.
function [S, fc] = sigmainv(z, M) if z == 0 S = 0; fc = 0; else [S, FS, info,out] = fzero(@(s)Fz(s,z,M), [0,1-eps/2]); if(info ~= 1) warning(['Klopoty dla z=', num2str(z), '; info=', num2str(info)]); end fc = out.funcCount; % zliczamy liczbe wywolan Fz end end % sigmainv function Z = Fz(S, z, M) % "z" jest parametrem Z = sigmafun(S, M)-z; end
Zanim przyjrzymy się meritum funkcji sigmainv, zwróćmy uwagę na kilka programistycznych szczegółów. Jak pamiętamy, fzero żąda funkcji jednego argumentu, dlatego, dla każdego zadanego Fz(S,z,M) — korzystając z mechanizmu funkcji anonimowej: funkcja
f = @(s)Fz(s,z,M)jest funkcją jednej zmiennej, z wartościami
Fz określiliśmy zaś jako funkcję lokalną dla sigmainv. Wreszcie, aby uniknąć konsternacji fzero dla Jest oczywiste, że eps/2], gdyż 1-eps/2 jest największą liczbą maszynową mniejszą od 1 (dlaczego?).
Pozornie ,,asekurancki” sposób zdefiniowania funkcji sigmainv, w której zawsze sprawdzamy wartość parametru info zwracaną przez fzero, jest w istocie bardzo ważną i sensowną decyzją, pozwalającą wstępnie zweryfikować wyniki. Wszak nie wiemy a priori, czy nasz solver sobie poradzi z
3.2. Transformacja zadania do wygodniejszej postaci
Chociaż wykres dostajemy bez trudu, stosując prostą metodę kontynuacji — biorąc za przybliżenie początkowe wartość z poprzedniego punktu wykresu (por. wykład z Matematyki Obliczeniowej II), to przychodzi nam nań czekać dość długo. Gdy ponownie spojrzymy na wykres
Gdy zadanie jest za trudne, należy zmienić… zadanie!
Tutaj po prostu zastąpimy ,,trudną” funkcję
Różnica między
Wyznaczanie wartości
function [S, fc] = sigmainv2(z,M) if z == 0 S = 0; fc = 0; else [S, FS, info, out] = fzero(@(s)Gz(s,z,M), [0,1]); if(info ~= 1) warning(['Klopoty dla z=', num2str(z), '; info=', num2str(info)]); end fc = out.funcCount; % zliczamy liczbe wywolan Gz end end % sigmainv2 function Z = Gz(S, z, M) % "z" jest parametrem p = 2/(1-M); Z = 1 - S - ((p - S)./(p+z)).^(p/2); end
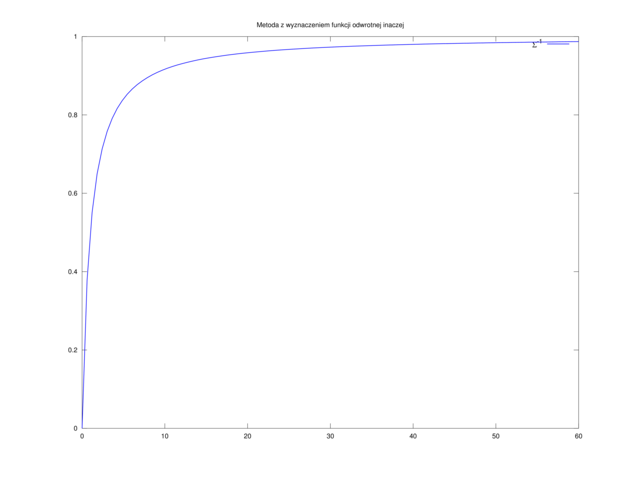
Faktycznie, dzięki tej zmianie wykres
3.3. A może wystarczy po prostu… wziąć większy młotek?
Na zakończenie warto być może zauważyć, że w dzisiejszych czasach obliczenia są na tyle tanie, że nie zawsze warto odwoływać się do aż tak wyrafinowanych metod. Gdyby naszym głównym zadaniem było narysowanie, wyłącznie w celach poglądowych, jednego wykresu na odcinku sigmafun: nasz komputer najpewniej i tak jest wystarczająco szybki, by z tym sobie błyskawicznie poradzić. Komenda logspace(k,m,N) pozwala wygenerować zestaw
Generując więc zestaw punktów skupiających się wokół
N = 10000; s = 1-logspace(-13,0,N); % punkty zagęszczają się wykładniczo wokół 1 Z = sigmafun(s,M); good = find(Z<=60); % odrzucamy te, które wykraczają poza zakres zmiennej "z" plot(Z(good), s(good));
udałoby się nam w ten sposób (nawet jeszcze szybciej, niż poprzednimi metodami!) ,,dociągnąć” wykres
(Ale i tutaj ważne jest wyczucie: gdyby nieopatrznie położyć s = 1-logspace(-300,0,N), dostalibyśmy znacznie gorszy wynik).
Ćwiczenie 3.1
Czasami funkcja może być na tyle złośliwa, że zamiast zmieniać jest postać — jak to zrobiliśmy powyżej — możemy spróbować skorzystać z mniej wyrafinowanej, a za to ogólniejszej metody rozwiązywania równania nieliniowego