4. Reakcja enzymatyczna
4.1. Równanie Michaelisa–Menten
W jednym z prostszych modeli reakcji enzymatycznych pojawia się równanie Michaelisa–Menten, ustanawiające zależność szybkość reakcji
| (4.1) |
Współczynniki
| 0.25 | 0.30 | 0.40 | 0.50 | 0.70 | 1.00 | 1.40 | 2.00 | |
| 2.4 | 2.6 | 4.2 | 3.8 | 6.2 | 7.4 | 10.2 | 11.4 |
Naszym zadaniem jest wyznaczenie takich wartości parametrów
4.1.1. Nietrafione uproszczenia
Wielu badaczy, jeszcze w czasach gdy obliczenia były zaporowo drogie, zaproponowało rozmaite transformacje powyższego problemu, pozwalające w ostatecznym rozrachunku sformułować zadanie jako liniowe zadanie najmniejszych kwadratów. Mając w pamięci numeryczną maksymę, że
Jeśli zadanie jest za trudne, należy… zmienić zadanie!
możemy ulec wrażeniu, że będzie to właściwa droga ku efektywnemu znalezieniu ,,optymalnych” wartości szukanych parametrów.
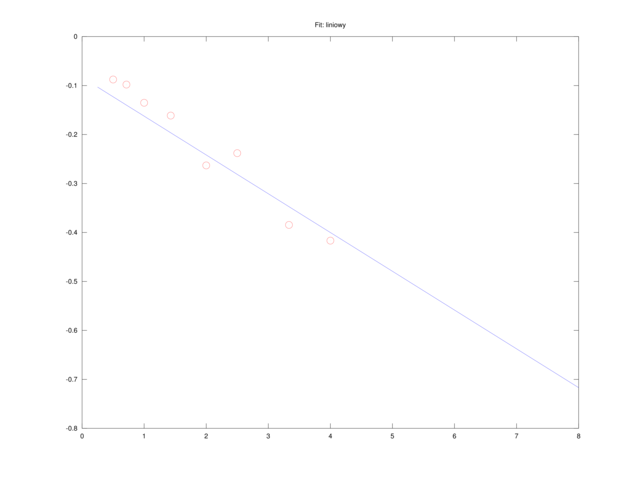
W przypadku zadania dopasowania
Równanie czysto liniowe
Mnożąc (4.1) stronami przez
| (4.2) |
które możemy oczywiście rozwiązać metodą najmniejszych kwadratów. Jeśli wektory kolumnowe S i v0 będą zawierać dane z pomiarów (odpowiednio:
e = ones(size(S),1); A = [1./S, -1./v0]; b = -e; x = A \ b; V = x(2); Km = x(1);spowodują wyznaczenie
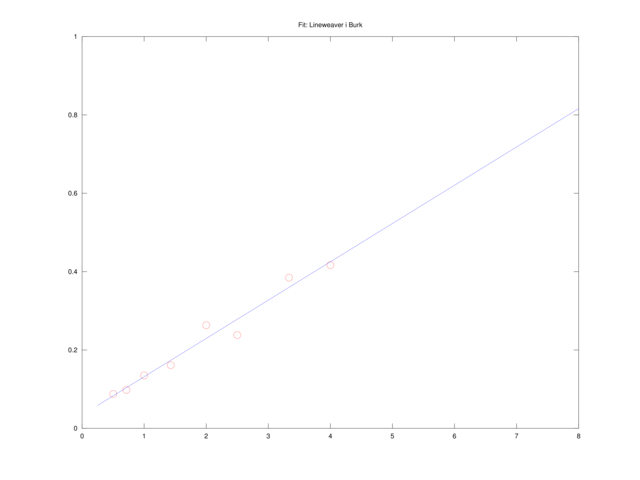
Równanie Lineweavera i Burka
Jeśli poprzednio wyprowadzone równanie podzielimy przez
które jest liniowe względem pomocniczych zmiennych
Analogicznie jak poprzednio, możemy znaleźć wartości
Rozwiążemy je w Octave, korzystając z operatora ,,\”, sekwencją komend:
A = [1./S, e]; b = 1./v0; x = A \ b; V = 1/x(2); Km = x(1)*V;
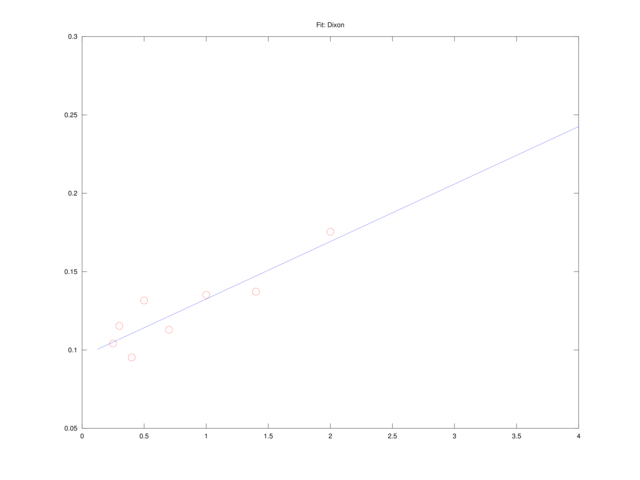
Równanie Dixona
Mnożąc równanie Lineweavera i Burka przez
liniowe w pomocniczych zmiennych
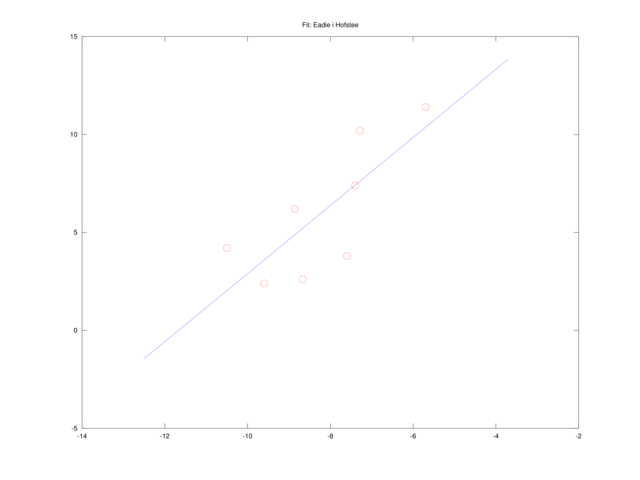
Równanie Eadie i Hofstee
Mnożąc wreszcie równanie liniowe (4.2) przez
które jest liniowe w oryginalnych zmiennych,
Ćwiczenie 4.1
Dla danych podanych w tabeli na początku rozdziału, wyznacz każdym z opisanych sposobów współczynniki
Przykładowe rozwiązania znajdują się w listingu w dalszej części wykładu. Swoją odpowiedź możesz porównać z tabelką w następnym rozdziale.
4.1.1.1. Krytyka metod prowadzących do liniowego zadania najmniejszych kwadratów
Powstaje więc — bynajmniej nie filozoficzne, ale czysto praktyczne — pytanie, która z metod jest ,,lepsza”, czyli która z nich da najlepsze możliwe dopasowanie (przy rozsądnym koszcie). Otóż wszystko zależy od tego, co będziemy rozumieli pod pojęciem ,,najlepsze”: wszak z definicji każde z uzyskanych przez nas rozwiązań było najlepsze, jako rozwiązanie zadania minimalizacji residuum postaci
Ponieważ ,,naturalnym” sformułowaniem naszego zadania było (4.1), wydaje się równie naturalnym postawienie i ocena rozwiązania w sensie nieliniowego zadania najmniejszych kwadratów:
| (4.3) |
Jeśli porównać wartości
| równanie | uwarunkowanie ( | |||
| Lineweaver i Burk | 29.43 | 2.88 | 1.71 | 12.1 |
| Dixon | 27.27 | 2.61 | 1.58 | 7.13 |
| Eadie i Hofstee | 20.27 | 1.74 | 2.65 | 874 |
| liniowe | 12.00 | 0.95 | 23.40 | 3170 |
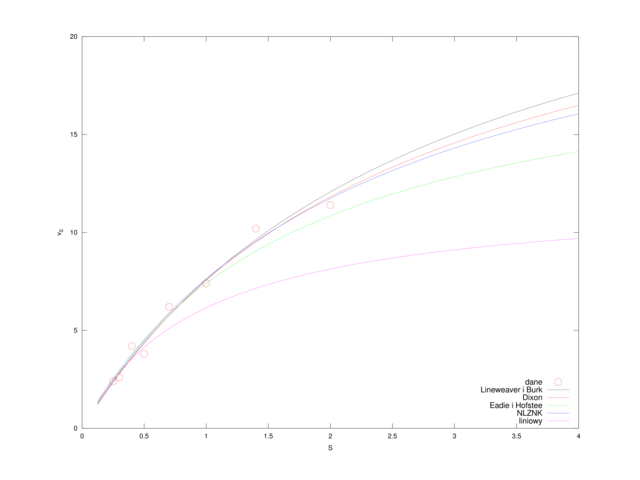
A więc w tym sensie, zdecydowanie najlepsze rezultaty dało dopasowanie metodą Dixona (por. także rysunek 4.5). Co więcej, okazuje się, że metody prowadzące do liniowej zależności od
Sensowne wyniki dają metody Lineweaver i Burk oraz Dixona, ale… czy nie można jeszcze lepiej? Wszak możemy spróbować rozwiązać wprost nieliniowe zadanie najmniejszych kwadratów (4.3), na przykład korzystając z solvera sqp, dostępnego w Octave.
4.1.2. Rozwiązanie nieliniowego zadania najmniejszych kwadratów
Solversqp jest narzędziem służącym do rozwiązywania znacznie bardziej złożonych zadań optymalizacji, dlatego jego użycie bywa skomplikowane. Ale w naszym prostym przypadku — minimalizacji bez ograniczneń, dla funkcjonału kwadratowego — nie będziemy musieli podawać mu zbyt wielu parametrów. Najpierw jednak zdefiniujemy funkcjonał, który będziemy minimalizować:
% (X(1), X(2)) <---> (V, K) F = @(X,S) (X(1)*S)./(X(2)+S); phi = @(X) sumsq(v0 - F(X,S));
Jak widać, zaczęliśmy od określenia funkcji
która pojawia się w definicji (4.1) i w (4.3), i która z pewnością nam się przyda: na przykład do narysowania wykresu phi jest anonimową funkcją tylko jednego argumentu, X, to w jej definicji zostaną użyte wcześniej przez nas zdefiniowane wektory S i v0, zawierające dane zadania. Dzięki temu, łatwo nam będzie wyznaczyć sumę kwadratów współrzędnych wektora v0 - F(X,S) — do tego właśnie służy funkcja Octave sumsq.
Teraz wystarczy wywołać solver sqp na naszym funkcjonale
% podane na wejściu sqp parametry (V, Km) zostały wyznaczone metodą Dixona [x, phix, info, iter, nphi] = sqp([V;Km], phi) V = x(1); Km = x(2);
W wyniku dostajemy info, liczba wykonanych iteracji iter, oraz wywołań funkcjonału nphi. Pożądana wartość info to, zgodnie z manualem, 101: zakończenie z powodu nikłego postępu iteracji. Musimy jednak pamiętać, że znalezione minimum może być jedynie minimum lokalnym i wybór innego punktu startowego może dać w rezultacie znacznie lepszy (lub gorszy) wynik.
Podsumowując, w dzisiejszych czasach, gdy nawet dość zaawansowae obliczenia są (w miarę) łatwe i tanie, nie powinniśmy bać się nieliniowości. Pamiętajmy także, że jeśli tylko możemy sensownie wspomóc się przybliżeniem uzyskanym na drodze rozsądnej linearyzacji — warto z tej opcji skorzystać.
Na marginesie dodajmy, że opisane przez nas wcześniej metody sprowadzenia zadania do zadania liniowego, są wciąż rutynowo stosowane w innych zadaniach dopasowywania do punktów pomiarowych wykresu, na przykład postaci
S = [0.25 ; 0.30; 0.40; 0.50; 0.70; 1.00; 1.40; 2.00];
v0 = [2.4; 2.6; 4.2; 3.8; 6.2; 7.4; 10.2; 11.4];
F = @(X,S) (X(1)*S)./(X(2)+S);
fitfun = @(X) sumsq(v0 - F(X,S));
function cbA = lsqcond(A, b, x, tol)
if nargin < 4
tol = 1e2;
end
c = norm(A*x)/norm(b);
t = norm(A*x-b)/norm(A*x);
condA = cond(A);
cb = condA/c;
cA = (condA^2)*t + condA;
cbA = cb+cA;
if (cbA) > tol
warning(['Uwarunkowanie zadania: ', num2str([cb, cA])]);
end
end
p = 0; n = 100;
s = linspace(0.125,4,n);
e = ones(size(S));
model = 5;
A = [1./S, -1./v0]; b = -e;
x = A \ b;
V(model) = x(2); Km(model) = x(1);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,1), A(:,2), 'ro'); hold on;
plot(1./s, -(1+x(1)./s)/x(2),'-b'); hold off;
title('Fit: liniowy'); pause(p);
print('-depsc','linear.eps');
% Lineweaver i Burk
model = 1;
A = [1./S, e]; b = 1./v0;
x = A \ b;
V(model) = 1/x(2); Km(model) = x(1)*V(model);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,1), b, 'ro'); hold on;
plot(1./s, x(1)./s+x(2),'-b'); hold off;
title('Fit: Lineweaver i Burk'); pause(p);
print('-depsc','lib.eps');
% Dixon
model = 2;
A = [e, S]; b = S./v0;
x = A \ b;
V(model) = 1/x(2); Km(model) = x(1)*V(model);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,2), b, 'ro'); hold on;
plot(s, x(2)*s+x(1),'-b'); hold off;
title('Fit: Dixon'); pause(p);
print('-depsc','dixon.eps');
% Eadie i Hofstee
model = 3;
A = [-v0./S, e]; b = v0;
x = A \ b;
V(model) = x(2); Km(model) = x(1);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = lsqcond(A,b,x);
plot(A(:,1), b, 'ro'); hold on;
s3 = linspace(min(A(:,1))-2, max(A(:,1))+2, 100);
plot(s3, x(1)*s3+x(2),'-b'); hold off;
title('Fit: Eadie i Hofstee'); pause(p);
print('-depsc','eih.eps');
% nonlinear fit; X = (V,Km)
model = 4;
[x, fitfunx, info, iter, nF, lambda] = sqp([V(2);Km(2)], fitfun);
V(model) = x(1); Km(model) = x(2);
resid(model) = fitfun([V(model),Km(model)]);
cbA(model) = NA;
if info ~= 101
warning('SQP: problemy z rozwiazaniem zadania');
end
printf('+------+---------+--------+----------+----------+\n');
printf(' Model | V | K | resid | cond\n');
printf('+------+---------+--------+----------+----------+\n');
printf(' %2d | %4.2f | %4.2f | %6.2f | %4.2e\n', [1:length(V);V;Km;resid;cbA]);
printf('+------+---------+--------+----------+----------+\n');
plotname = {'dane','Lineweaver i Burk','Dixon','Eadie i Hofstee','NLZNK','liniowy'};
plot(S, v0, 'ro');
hold on;
for i = 1:length(V)
plot(s, F([V(i),Km(i)],s) , ['-', num2str(i-1)]);
pause(p);
end
hold off;
xlabel('S'); ylabel('v_0');
legend(plotname, 'location', 'southeast');
print('-depsc','michaelis-fit.eps')
4.2. Różniczkowy model łańcucha reakcji enzymatycznych
W rozdziale 6. pracy [24] rozważa się model łańcucha trzech reakcji katalizowanych enzymatycznie. Niech
Wtedy kinetyka powyższego układu może być modelowana następującym zestawem równań różniczkowych zwyczajnych [24, równania (75)—(82)]11Podajemy go już po pewnych uproszczeniach.:
z parametrami
W tym celu w rutynowy sposób wyznaczymy rozwiązanie powyższego układu równań, korzystając z funkcji lsode. Najpierw jednak zapiszemy układ równań w formie takiej, by występowały w nim jedynie niewiadome
W naszych eksperymentach numerycznych przyjmiemy za [24]
Funkcja prawej strony miałaby więc postać12Jeżeli w definicji dX przypadkowo napiszesz dX = [ a -b; ..itd..], to interpreter Octave zrozumie, że chodzi o macierz o dwóch kolumnach, dX = [ a, -b; ..itd..]. Dlatego, powinniśmy tutaj konsekwentnie pisać dX = [ a - b; ..itd..] (z operatorem odejmowania otoczonym spacjami).
function dX = reaction(X,t) global a; global b; global c; global X6; global X7; global X8; global X9; global X10; dX = [a*(X7*(X8-X(1)))^c + b*(X(2)*(X8-X(1)))^c - (b+a)*X(1) ; a*X(1) + b*X(3) - b*(X(2)*(X8-X(1)))^c - a*(X(2)*(X9-X(3)))^c ; a*(X(2)*(X9-X(3)))^c + b*(X(4)*(X9-X(3)))^c - (b+a)*X(3) ; a*X(3) + b*X(5) - b*(X(4)*(X9-X(3)))^c - a*(X(4)*(X10-X(5)))^c ; a*(X(4)*(X10-X(5)))^c + b*(X6*(X10-X(5)))^c - (b+a)*X(5)]; end(dla większej skuteczności iloczyny postaci
global a; global b; global c; global X6; global X7; global X8; global X9; global X10; a = 2; b = 1; c = 4; X6 = X8 = X9 = X10 = 1; X7 = 1.425; T = 10; N = 800; t = linspace(0,T,N); X = lsode(@reaction, zeros(5,1), t); plot(t,X); pause(3); v = a*X(:,5) - b*(X6*(X10-X(:,5))).^c; plot(t,v)
Tradycyjnie, aby nieco upewnić się co do jakości otrzymanych wyników, powinniśmy przeprowadzić kilka symulacji z różnymi parametrami tolerancji błędu (i zbadać, czy przypadkiem nie padliśmy ofiarą aliasingu, czyli zbyt małej rozdzielczości wizualizacji, fałszującej rzeczywisty przebieg rozwiązania).
Ćwiczenie 4.2
Przeprowadź testy wizualnej i numerycznej jakości uzyskanego rozwiązania, zmieniając N (by zabezpieczyć się przed aliasingiem) oraz lsode_options (by zmniejszyć ryzyko wzięcia numerycznych artefaktów za prawdziwe własności rozwiązania).