Ponieważ na parametr C nie ma ograniczeń, możemy łatwo go wyeliminować z rozważań przyrównując do zera pochodną

gdzie x¯=1N⁢∑i=1Nxi i analogicznie y¯=1N⁢∑i=1Nyi.

W ten sposób zadanie zredukowało się do znalezienia wektora u=A,BT takiego, że

gdzie

Jest to więc nic innego, jak zadanie wyznaczenia wektora szczególnego¹⁵Więcej na temat wektorów i wartości szczególnych można dowiedzieć się np. w wykładzie z Matematyki Obliczeniowej II, w rozdziale dotyczącym rozkładu SVD macierzy. macierzy M, odpowiadającego najmniejszej wartości szczególnej. Rzeczywiście, jeśli M=U⁢Σ⁢VT i macierze U,V są ortogonalne, a

przy czym dla ustalenia uwagi σ1≥σ2≥0, to

a równość zachodzi gdy VT⁢x=0,1T, czyli dla x=v2.

Ponieważ w Octave znajduje się gotowa funkcja wyznaczająca pełny rozkład SVD zadanej macierzy, możemy pokusić się o implementację funkcji wyznaczenia A,B,C na podstawie punktów, których współrzędne na osiach O⁢X i O⁢Y podane są, odpowiednio, w talicach x i y:

function ABC = linefit(x,y)
x = x(:); y = y(:);
ABC = NaN(3,1);
xm = mean(x); ym = mean(y);
[U, S, V] = svd([x-xm, y-ym], 0); % ekonomiczny rozkład SVD
ABC(1:2) = V(:,end); % [A, B]
ABC(3) =  - ABC(1)*xm - ABC(2)*ym;
end

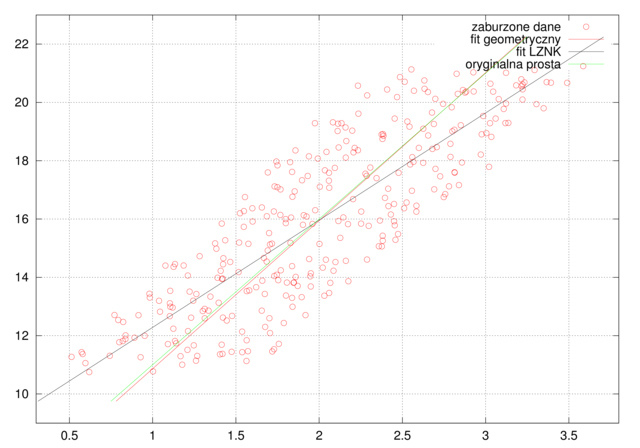
Aby przetestować działanie naszego kodu, zaburzymy losowo punkty prostej y=5⁢x+6 i sprawdzimy, co wyjdzie. Porównamy także nasz (geometryczny) fit z dopasowaniem na podstawie standardowej metody najmniejszych kwadratów.

W celu wygodnego rysowania prostej zadanej w postaci uwikłanej, naprędce opracujemy funkcję lineplot, której listing zamieszczamy poniżej.

function lineplot(ABC, X, Y, color)
if nargin < 4
	color = '';
end
xmin = X(1); xmax = X(2);
ymin = Y(1); ymax = Y(2);
A = ABC(1); B = ABC(2); C = ABC(3);
if abs(A/B) <= 1
	plot(X, (-C-A*X)/B, ['-',color]);
else
	plot((-C-B*Y)/A, Y, ['-',color]);
end
end

Teraz możemy rozpocząć testy, korzystając na przykład z kodu poniższej postaci:

a = 5; b = 6;
x = linspace(1,3,300);
y = a*x + b;
x = x+0.6*(2*rand(size(x))-1);
y = y+0.6*(2*rand(size(y))-1);
% fit geometryczny
ABC = linefit(x,y);
% fit LZNK
ba = [ones(size(x)); x]'\y';
plot(x,y,'or');
hold on;
lineplot(ABC,[0,4],[min(y)-1,max(y)+1],'r');
lineplot([ba(2),-1,ba(1)],[0,4],[min(y)-1,max(y)+1],'k');
lineplot([a,-1,b],[0,4],[min(y)-1,max(y)+1],'g');
hold off;
legend('zaburzone dane','fit geometryczny','fit LZNK','oryginalna prosta');
grid on;

Ponieważ zadanie minimalizacji tym razem dotyczy bardziej skomplikowanego funkcjonału nieliniowego, użyjemy standardowej procedury optymalizacji nieliniowej w Octave, sqp.

function d = residgeom(X,x,y)
	% a = X(1); b = X(2); r = X(3);
	d = sumsq( sqrt((x-X(1)).^2 + (y-X(2)).^2) - X(3));
end

function [S,dist,info] = fitcircle1(S0,x,y)
% S = (a,b,r)
[S,dist,info] = sqp(S0,@(X)residgeom(X,x,y));
end

Funkcja residgeom wyznacza wartość funkcjonału f⁢a,b,r, przy czym przekazujemy jej wszystkie parametry funkcjonału w pierwszym argumencie, w postaci wektora X. Musimy tak zrobić, bo sqp spodziewa się funkcji jednego argumentu — taką tworzymy w postaci funkcji anonimowej

@(X)residgeom(X,x,y)

Jakkolwiek dokonany przez nas wybór parametrów zadania: a,b,r, jest niewątpliwie kuszący, to jednak, gdy punkty xi,yi są prawie współliniowe, wyznaczany promień r może być bardzo duży w porównaniu do współrzędnych środka a,b. Ponadto małe zaburzenia położenia punktów xi,yi mogą prowadzić do dużych skoków wielkości r (a także — położenia środka okręgu), dlatego warto zadanie sformułować inaczej.

Okrąg S możemy opisać za pomocą standardowego równania krzywej drugiego stopnia,

Ponieważ wynika stąd, że

Jak podaje [1], Pratt zasugerował warunek normalizacyjny

Ponadto wówczas odległość di punktu xi,yi od okręgu jest równa

zatem musimy minimalizować funkcjonał

z ograniczeniem

To zadanie po raz kolejny zrealizujemy za pomocą funkcji sqp:

function d = residgeom2(X,x,y)
	A = X(1); B = X(2); C = X(3); D = X(4);
	P = A*(x.^2 +y.^2) + B*x + C*y + D;
	d = sumsq(2*(P./(1+sqrt(1+4*A*P))));
end

function d = constr(X)
d = X(2)^2 + X(3)^2 - 4*X(1)*X(4) - 1;
end

function [S,dist,info] = fitcircle2(S0,x,y)
% S = (A,B,C,D)
c = zeros(4,1);
c(1) = 1/(2*S0(3)); c(2:3) = -2*c(1)*S0(1:2); c(4) = (c(2)^2 + c(3)^2 - 1)/(4*c(1));

[c,dist,info] = sqp(c, @(X)residgeom2(X,x(:),y(:)), @constr);
S = [-c(2:3)/(2*c(1)); sqrt(c(2)^2 + c(3)^2 - 4*c(1)*c(4))/(2*abs(c(1)))];
end

Jakkolwiek ostatnią linijkę kodu moglibyśmy teoretycznie zastąpić tańszym S = [-c(2:3); 1]/(2*c(1)), to jednak bezpieczniej będzie zrobić tak, jak powyżej — bo warunek B2+C2-4⁢A⁢D=1 może nie być idealnie spełniony.

Pozostaje jeszcze pytanie, w jaki sposób będziemy mogli sensownie wyznaczyć początkowe przybliżenie S0. Nadspodziewanie dobrym kandydatem na S0 jest (patrz [1]) okrąg spełniający tzw. algebraiczny warunek dopasowania, tzn. minimalizujący, przy ograniczeniu B2+C2-4⁢A⁢D=1, sumę kwadratów residuum równania okręgu:

gdzie ri jest zadane przez ri=A⁢xi2+yi2+B⁢xi+C⁢yi+D.

Jest to więc — bardzo podobnie jak widzieliśmy to w przypadku fitowania prostej — zadanie najmniejszych kwadratów dla u=A,B,C,D

gdzie

Niestety, macierz K nie jest dodatnio określona, co komplikuje algorytm rozwiązywania tego zadania.

Funkcja Lagrange'a jest postaci

zatem koniecznym warunkiem dla ekstremum jest

Ponieważ Lu⁢u,λ=MT⁢M⁢u-λ⁢K⁢u, to pierwszy warunek oznacza po prostu, że para λ,u jest parą własną powyższego uogólnionego zadania własnego,

Wprowadzając (ekonomiczny) rozkład QR macierzy M,

mamy równoważnie RT⁢R⁢u-λ⁢K⁢u i stąd R⁢u,λ musi być parą własną macierzy R⁢K-1⁢RT. Ponieważ macierz K-1 ma wartości własne 1,1,1/2,-1/2, to macierz R⁢K-1⁢RT (na mocy tw. Sylvestera) także ma dokładnie jedną wartość własną ujemną, a pozostałe trzy — dodatnie.

Mnożąc stronami (7.1) przez uT dostajemy

na mocy warunku uT⁢K⁢u=1. Ponieważ M⁢u22≥0, interesująca nas λ nie może być ujemna. Ze względu na to, że poszukiwane przez nas u musi minimalizować M⁢u22, znaczy to, że minimum zostanie przyjęte równe najmniejszej dodatniej wartości własnej B. W takim razie szukana przez nas para własna to para odpowiadająca najmniejszej dodatniej wartości własnej macierzy R⁢B-1⁢RT.

Stąd jednym ze sposobów implementacji powyższego algorytmu wyznaczenia u — a tym samym okręgu spełniającego wymieniony na początku tej sekcji algebraiczny warunek dopasowania — może być funkcja:

function [S,dist,info] = fitcircle3(x,y)
x = x(:); y = y(:);
invB = [0 0 0 -0.5; 0 1 0 0; 0 0 1 0; -0.5 0 0 0]; % $B^{-1}$ explicite 
X = [x.^2+y.^2, x, y, ones(size(x))];
[Q R] = qr(X,0);
[V L] = eig(R*invB*R'); 
[L i] = sort(diag(L));
c = R \ V(:,i(2)); % interesuje nas druga najmniejsza w.wl, a raczej: wektor
S = [-c(2:3)/(2*c(1)); sqrt(c(2)^2 + c(3)^2 - 4*c(1)*c(4))/(2*abs(c(1)))];
dist = residgeom(S,x,y);
info = 1;
end

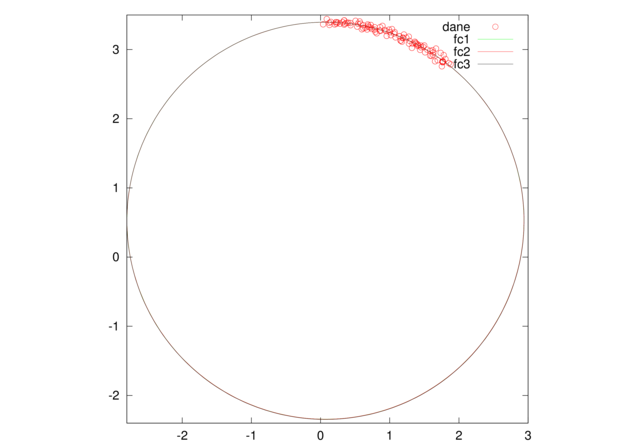
Poniżej przytaczamy przykładowy skrypt dopasowujący okrąg do zadanych punktów trzema opisanymi wcześniej metodami.

t = linspace(0,0.2*pi,100)';
X = 3*sin(t)+0.2*rand(size(t));
Y = 3.35*cos(t)+0.1*rand(size(t));

XY = [X,Y];
e = fitcircle3(X,Y);
c = fitcircle1(e,X,Y);
d = fitcircle2(e,X,Y);
[e c d]

t = linspace(0,2*pi,300);
plot(X,Y,'ro');
axis('square');
hold on;
plot(c(1) + c(3)*sin(t),c(2)+c(3)*cos(t),'g-');
plot(d(1) + d(3)*sin(t),d(2)+d(3)*cos(t),'r-');
plot(e(1) + e(3)*sin(t),e(2)+e(3)*cos(t),'k-');
plot(X,Y,'ro');
hold off;
legend('dane', 'fc1', 'fc2', 'fc3');
[residgeom(c,X,Y), residgeom(d,X,Y), residgeom(e,X,Y)]