Siecią nazywać będziemy skończony graf G=W,S;k,p wraz z dwiema funkcjami V⁢:W→R przypisującą każdemu wierzchołkowi liczbę rzeczywistą V⁢w zwaną potencjałem i C⁢:S→R przypisującą każdej krawędzi koszt przepływu. Ponieważ zawiera wierzchołki i krawędzie więc, dla uniknięcia nieporozumień, wierzchołki sieci będziemy nazywać węzłami zaś zorientowane krawędzie strzałkami.

Zagadnienie przepływy w sieciach ( o nieograniczonej przepustowości ) polega na znalezieniu schematu przepływu o minimalnych kosztach, wyrównującego potencjały.

Modelem matematycznym takiego zagadnienia będzie:

Jako zmienne wybieramy zbiór xs⁢|⁢s∈S indeksowany strzałkami grafu.

M⁢i⁢n⁢⁢x0=∑s∈S⁢C⁢s⁢xs na obszarze opisanym nierównościami:

∀w∈W⁢∑s∈S⁢|p⁢s=w⁢xs-∑s∈S⁢|k⁢s=w⁢xs=V⁢w

∀s∈S⁢xs≥0.

Zauważmy, macierz opisująca powyższe równania ma wiersze indeksowane węzłami a kolumny, z prawej strony kreski, indeksowane strzałkami s (lub zmiennymi xs ). Ponadto kolumna odpowiadająca strzałce s ma zera, jedną 1 w wierszu o indeksie p⁢s i jedną -1 w wierszu o indeksie k⁢s. W przypadku grafu ukorzenionego strzałką s1, dochodzi kolumna o indeksie s1, która ma zera i jedną 1 w wierszu o indeksie p⁢s1

Jak zsumujemy wszystkie równania, dla grafu nieukorzenionego, lewa strona zredukuje się do 0 i otrzymamy:

0=∑w∈W⁢V⁢w

A zatem ten układ równań jest zależny i jeżeli suma potencjałów jest niezerowa to jest sprzeczny. Zagadnienie gdy ∑w∈W⁢V⁢w=0 nazywamy zrównoważonym.

Zajmijmy się teraz zrównoważonym zadaniem przepływu w sieci, która jest grafem spójnym. Okazuje się, że w takim przypadku po ukorzenieniu grafu w dowolnym wierzchołku równania stają się liniowo niezależne a każdy układ bazowy jest wyznaczony przez pewne drzewo spinające. Dokładniej.

Twierdzenie 14.1 w dalszej części będziemy używać poprzez następujący wniosek.

Do dowodu części b) twierdzenia 14.1 użyjemy następującego lematu.

Algorytm sympleks w sieciach.

Algorytm ten będziemy ilustrować przykładem.

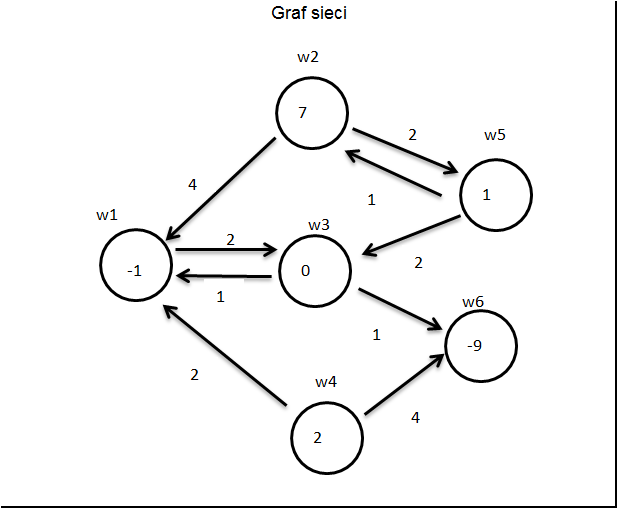
Dane zadanie opisane grafem

Liczby w węzłach opisują potencjały zaś na strzałkach koszty.

Jak widać suma potencjałów jest zerowa więc zadanie jest zbilansowane.

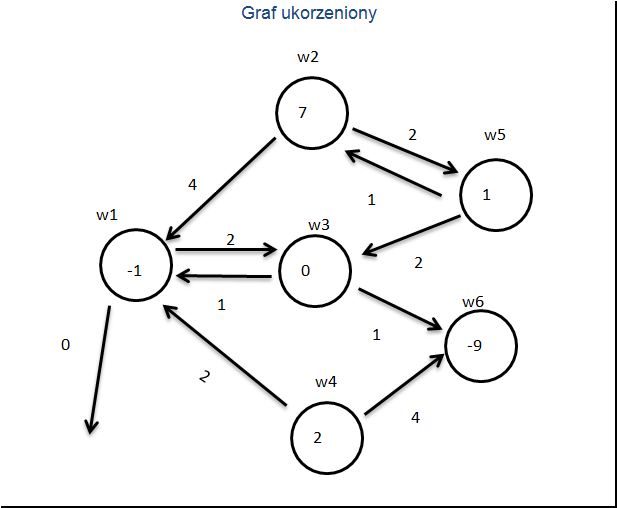
Ukorzeniamy graf w węźle w1.

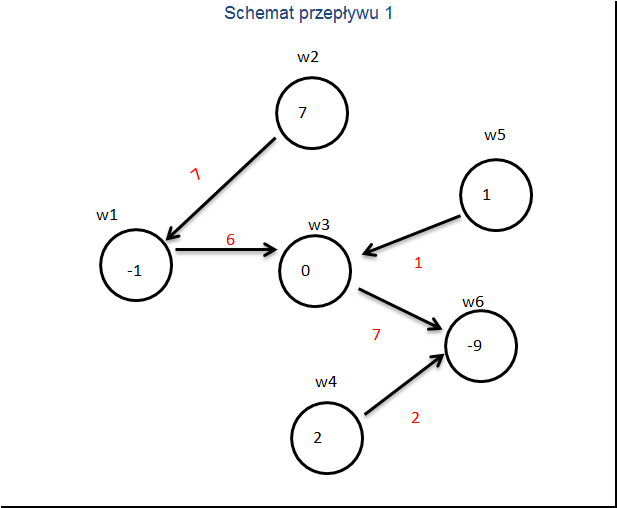
Do rozpoczęcia algorytmu potrzebujemy wierzchołek startowy. Niech będzie nim następujące drzewo spinające:

Czerwone liczby oznaczają wartości zmiennych czyli liczba towaru przepływająca przez strzałkę.

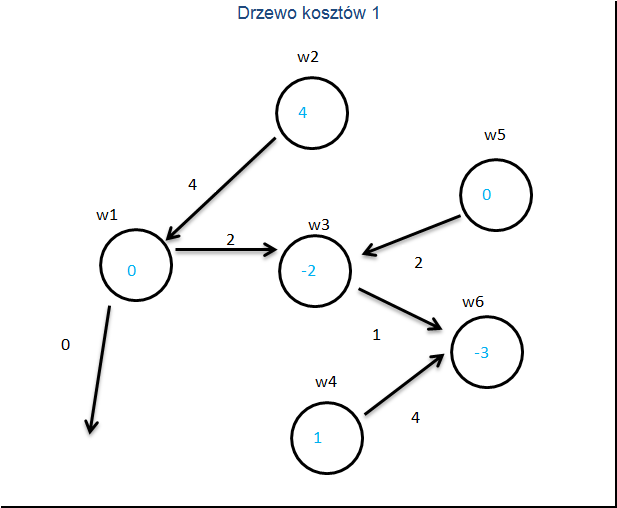
Krok 1 TEST OPTYMALNOŚCI

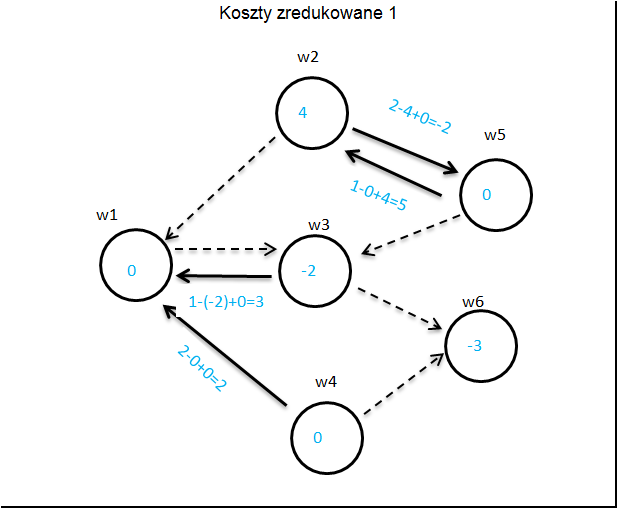
Budujemy pomocnicze drzewo kosztów. Koszty podróży po strzałkach są te same a liczby w węzłach obrazują koszt spływu jednostki towaru przez korzeń. W przypadku podróży pod prąd koszt strzałki liczymy ze znakiem minus.

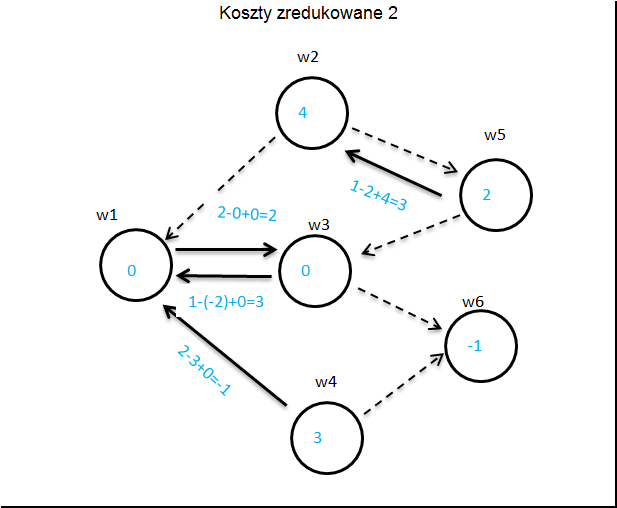
Teraz wyliczamy koszty zredukowane.

Liczymy koszty zredukowane zgodnie z zasadą: Na węźle wi umieszczamy liczbę di z drzewa kosztów. Następnie koszt każdej strzałki wychodzącej z wi zmniejszamy o di zaś koszt każdej strzałki przychodzącej do wi zwiększamy o di. Wartość funkcji celu zmieni się przy tej ope4racji o stałą di⋅V⁢wi. Metoda obliczania wartości węzłów w drzewie kosztów wymusza zerowe koszty strzałek użytych w schemacie przepływu ( zerowe koszty zmiennych bazowych ).

Koszt zredukowany strzałki si,j między węzłami wi awj wynosi ci,j′=ci,j-di+dj.

Jeżeli wszystkie strzałki mają koszt nieujemny to STOP badany schemat jest optymalny.

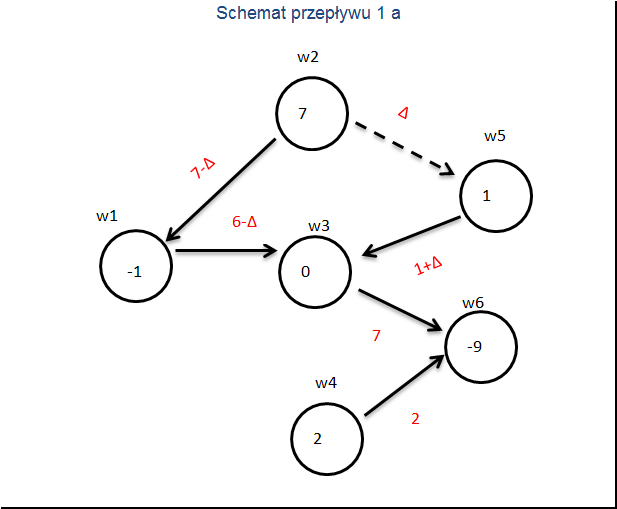
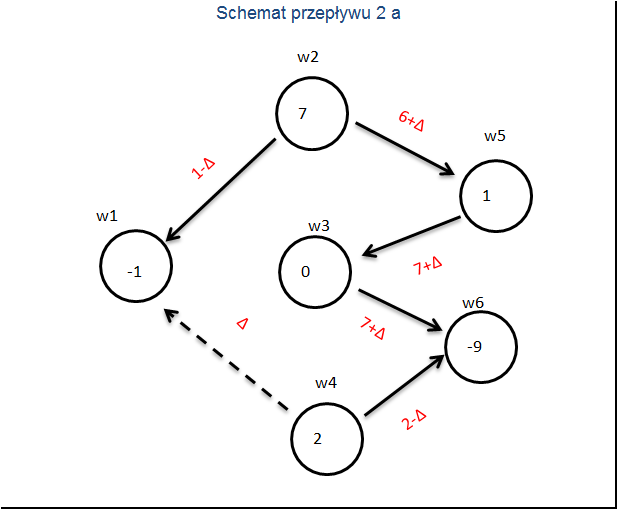
Krok 2. WYBÓR KOLUMNY POPRAWIAJĄCEJ

Wybieramy teraz strzałkę o ujemnym koszcie i dołączamy ją do drzewa. W naszym przykładzie jest to strzałka zaznaczona linią przerywaną z w2 do w5.

Krok 3. WYBÓR ELEMENTU CENTRALNEGO

Pojawia się cykl po którym staramy się przepchnąć jak najwięcej towaru. Dołączoną strzałką podróżuje Δ jednostek a pozostałymi strzałkami o Δ mniej lub więcej w zależności od ich zwrotu. Ponieważ zmienne są nieujemne jako Δ wybieramy minimum z kosztów strzałek przeciwnie zorientowanych niż dodana. W naszym przykładzie Δ=m⁢i⁢n⁢6,7=6.

Teraz z grafu wyrzucamy jedną ze strzałek po której nie płynie towar. W naszym przykładzie jest to strzałka z w1 do w3. W ten sposób otrzymaliśmy nowy schemat przewozu, który jest drzewem a więc wierzchołkiem obszaru dopuszczalnego. Funkcję celu poprawiliśmy o Δ pomnożone przez koszt dołączonej strzałki. W naszym przykładzie wyrzucamy strzałkę z w1 do w3.

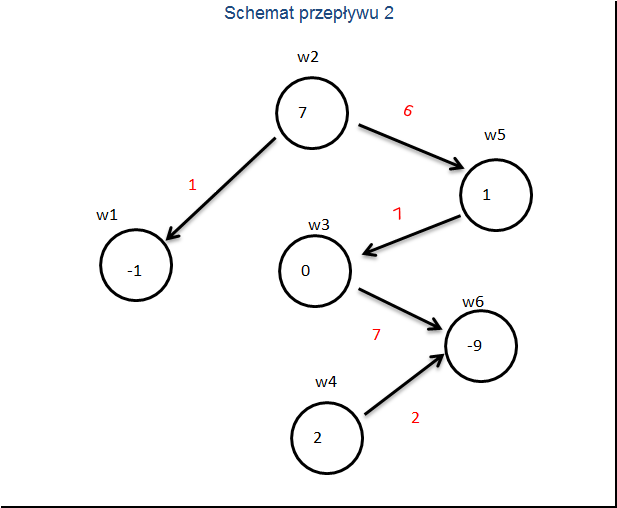
GO TO krok 1

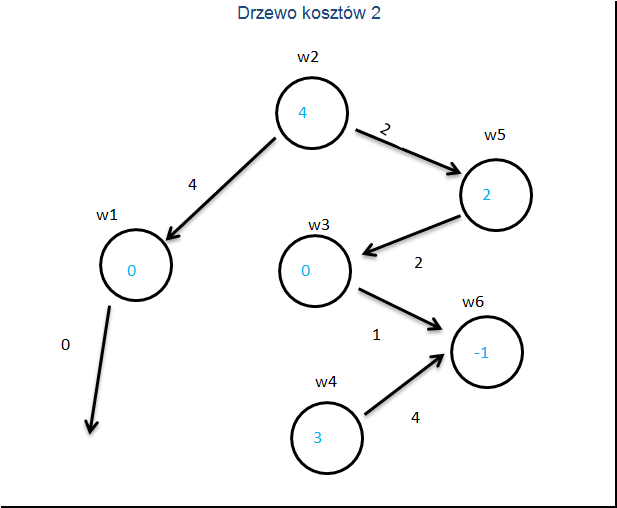
Budujemy drugie drzewo kosztów.

i wyliczamy koszty zredukowane drugiego schematu przepływu.

Tym razem ujemny koszt ma strzałka z w4 do w1. Dołączamy ją i otrzymujemy cykl:

W naszym przykładzie Δ=m⁢i⁢n⁢1,2=1 więc wyrzucamy strzałkę z w2 do w1. Otrzymujemy trzeci schemat przepływu.

Znowu liczymy koszty zredukowane.

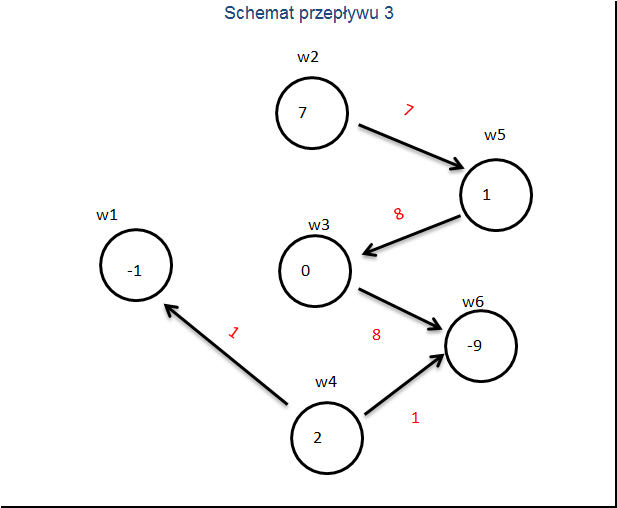
[0.5]KZ3Koszty zredukowane 3

Są one nieujemne więc schemat trzeci jest optymalny.

Dwufazowa metod sympleks.

Dana jest sieć G=W,S;k,p wraz z potencjałem V. Wprowadzamy dodatkowy (sztuczny ) węzeł o potencjale 0 i strzałki łączące sztuczny węzeł ze wszystkimi pozostałymi tak skierowane by potencjały mogły się wyrównać. Następnie wprowadzamy sztuczną funkcję celu nadając starym strzałkom koszt 0 a sztucznym koszt 1. Dalej stosujemy prosty algorytm sympleks. Jeżeli nie uda się uzyskać przepływu o koszcie 0 to znaczy, że wyjściowe zadanie jest sprzeczne. W przeciwnym przypadku uzyskamy przepływ będący wierzchołkiem obszaru dopuszczalnego.

Przypadek niezbilansowany.

Przypadek niezbilansowany sprowadzamy do zbilansowanego wprowadzając sztuczny węzeł o potencjale przeciwnym do sumy pozostałych potencjałów i strzałki łączące sztuczny węzeł ze wszystkimi pozostałymi. Jeżeli sztuczny węzeł ma potencjał dodatni to wszystkie sztuczne strzałki z niego wychodzą. Jeżeli ujemny to wszystkie sztuczne strzałki mają w nim swój koniec. Dalej stosujemy prosty algorytm sympleks.

Przykład i zadanie w tym wykładzie pochodzą z egzaminów prof. W. Ogryczaka.