« 13. Metody stochastyczne w finansach  Spis treści  15. Metody stochastyczne w finansach – cd »  

Zagadnienia

14. Metody stochastyczne w finansach - cd

14.1. Dominacja stochastyczna

Oczekiwana użyteczność zależy od wyboru funkcji użyteczności. Zachodzi pytanie, czy można ocenić, która z dwóch inwestycji jest lepsza dla wszystkich inwestorów niezależnie od ich indywidualnych preferencji. Postaramy się odpowiedzieć na to pytanie, korzystając z pojęcia dominacji stochastycznej.

Niech K1 i K2 oznaczają zmienne losowe.

Definicja 14.1

Mówimy, że K1 dominuje nad K2 gdy

K1≥K2⁢ p.n. ,

czyli PK1<K2=0.

Definicja 14.2

Mówimy, że K1 dominuje nad K2 w sensie dominacji stochastycznej rzędu pierwszego, gdy

∀x∈R⁢⁢⁢⁢F1⁢x≤F2⁢x,

gdzie Fi oznacza dystrybuantę zmiennej losowej Ki.

Piszemy wówczas:

K1≥F⁢S⁢DK2.

Relacja FSD nie zależy od wyboru definicji dystrybuanty. Jeżeli K1 dominuje nad K2 w sensie dominacji stochastycznej rzędu pierwszego dla dystybuant prawostronnie ciągłych (Fi⁢x=PKi≤x), to dominuje również w sensie dominacji stochastycznej rzędu pierwszego dla dystybuant lewostronnie ciągłych (Fi⁢x=PKi<x) i na odwrót. Ale dla ustalenia uwagi, w dalszym ciągu będziemy używać dystrybuant prawostronnie ciągłych (zgodnie z [21, 26]).

Dystrybuanta F jest funkcją nieujemną i ograniczoną, zatem zawsze istnieje granica skończona lub nieskończona całek ⁢∫yxF⁢t⁢d⁢t⁢ gdy y zbiega do -∞, czyli uogólniona całka niewłaściwa ⁢∫-∞xF⁢t⁢d⁢t⁢ jest zawsze określona.

Definicja 14.3

Mówimy, że K1 dominuje nad K2 w sensie dominacji stochastycznej rzędu drugiego, gdy

∀x∈R⁢⁢⁢⁢∫-∞xF1⁢t⁢d⁢t≤∫-∞xF2⁢t⁢d⁢t,

gdzie Fi dystrybuanta Ki, a całki są całkami uogólnionymi.

Piszemy wówczas:

K1≥S⁢S⁢DK2.

Zauważmy, że w przypadku dominacji stochastycznej rzędu pierwszego i drugiego zmienne losowe K1 i K2 nie muszą być określone na tej samej przestrzeni probabilistycznej. Ponadto, jeśli nawzajem nad sobą dominują, to mają ten sam rozkład (F1=F2). Zatem relacje dominacji stochastycznej, rzędu pierwszego i drugiego, są relacjami quasi-porządku na zbiorach zmiennych losowych, indukującymi relacje częściowego porządku na zbiorach ich rozkładów.

Uwaga. Mamy następujące zależności:

Dominacja ⇒ FSD ⇒ SSD .

Pokażemy teraz, jakie związki zachodzą między kryterium maksymalizacji oczekiwanej użyteczności a dominacją stochastyczną pierwszego i drugiego rzędu.

Twierdzenie 14.1

Niech K1 i K2 zmienne losowe. Wówczas następujące warunki są równoważne:
1. K1≥F⁢S⁢DK2;
2. Dla każdej niemalejącej funkcji φ⁢ mamy:
E⁢φ⁢K1≥E⁢φ⁢K2 lub obie wartości oczekiwane są nieokreślone lub E⁢φ⁢K1=+∞ lub E⁢φ⁢K2=-∞;
3. Istnieją zmienne losowe K1′ i K2′ o tym samym rozkładzie co odpowiednio K1 i K2, takie, że

K1′≥K2′.

Dowód.
1⇒3.
Skorzystamy ze standardowej konstrukcji (patrz [21] §5.3 zad. 2). Zmienne losowe K1′ i K2′ zdefiniujemy na nowej przestrzeni probabilistycznej. Jako zbiór zdarzeń elementarnych weźmiemy otwarty odcinek jednostkowy (Ω=0,1), a jako prawdopodobieństwo miarę Lebesgue'a μ na tym odcinku. Niech

Ki′⁢t=sup⁡u:PKi≤u<t.

Jak łatwo sprawdzić, Ki′ i Ki mają ten sam rozkład prawdopodobieństwa. Rzeczywiście dla dowolnego x∈R

μ⁢t:Ki′⁢t≤x=μ⁢t:sup⁡u:PKi≤u<t≤x=
=μ(0,P(Ki≤x))=P(Ki≤x).

Pozostaje pokazać, że K1′ dominuje nad K2′. Z pierwszej dominacji stochastycznej K1 wynika, że

∀u⁢⁢⁢⁢PK1≤u≤PK2≤u.

Zatem

∀t>0⁢⁢⁢⁢sup⁡u:PK1≤u<t≥sup⁡u:PK2≤u<t,

czyli dla dowolnego t ⁢⁢K1′⁢t≥K2′⁢t.

3⇒2.
Wartość oczekiwana zależy tylko od rozkładu, φ⁢Ki′ i φ⁢Ki mają ten sam rozkład, a więc E⁢φ⁢Ki′=E⁢φ⁢Ki lub obie są nieokreślone. Ponadto φ jest niemalejąca, zatem gdy wartości oczekiwane istnieją, to

E⁢φ⁢K1=E⁢φ⁢K1′≥E⁢φ⁢K2′=E⁢φ⁢K2.

2⇒1.
Zauważmy, że funkcje

φx⁢t=⁡0 dla t≤x1 dla t>x⁢

są niemalejące. Zatem dla dowolnego x∈R

PK1≤x=1-PK1>x=1-E⁢φx⁢K1≤
≤1-E(φx(K2))=1-P(K2>x)=P(K2≤x),

co daje K1≥F⁢S⁢DK2.

Wniosek 14.1

Niech h:I→R, I⊂R, będzie funkcją niemalejącą taką, że zmienne losowe K1 i K2 prawie na pewno przyjmują wartości z I

PK1∉I=PK2∉I=0.

Wówczas

K1≥F⁢S⁢DK2⟹h(K1)≥F⁢S⁢Dh(K2).

W szczególności dla a,m∈R i a>0

K1≥F⁢S⁢DK2⟺aK1+m≥F⁢S⁢DaK2+m.

Dowód.
Skorzystamy z pkt. 3 powyższego twierdzenia. Jeśli K1′ i K2′ mają ten sam rozkład co odpowiednio K1 i K2 i

K1′≥K2′,

to h⁢K1′ i h⁢K2′ mają ten sam rozkład co odpowiednio h⁢K1 i h⁢K2 i

h⁢K1′≥h⁢K2′.

Zatem

h(K1)≥F⁢S⁢Dh(K2).

Przejdziemy teraz do drugiej dominacji stochastycznej. Na początek pokażemy związek między całką z dystrybuanty, a wartością oczekiwaną.

Lemat 14.1

Dla dowolnej zmiennej losowej K o dystrybuancie F

∀x∈R⁢⁢⁢⁢E⁢K-x-=∫-∞xF⁢t⁢d⁢t.

Dowód.
Jak wiadomo ([21] Stwierdzenie 11 §5.6) wartość oczekiwana nieujemnej zmiennej losowej X jest równa całce z prawdopodobieństwa przekroczenia poziomu t po d⁢t,

E(X)=∫0∞P(X>t)dt.

Część ujemna K-x- jest z definicji nieujemna, zatem

E((K-x)-)=∫0∞P((K-x)->t)dt.

Ponieważ t≥0, to K-x->t wtedy i tylko wtedy, gdy K<x-t i

E((K-x)-)=∫0∞P((K<x-t)dt.

Po zamianie zmiennych, s=x-t, otrzymujemy

E((K-x)-)=∫-∞xP(K<s)ds=∫-∞xF(s)ds,

gdyż poza przeliczalną liczbą punktów F⁢s=PK<s.

Z powyższego wynika następująca charakteryzacja drugiej dominacji stochastycznej:

Wniosek 14.2
K1≥S⁢S⁢DK2⇔∀x∈RE((K1-x)-)≤E((K2-x)-).

Pokażemy teraz, że gdy K ma skończoną wartość oczekiwaną, to funkcja

G⁢x=∫-∞xF⁢t⁢d⁢t

ma prawostronną asymptotę ukośną x-E⁢K.

Lemat 14.2

Dla dowolnej zmiennej losowej K o dystrybuancie F i skończonej wartości oczekiwanej (K∈L1)

limx→+∞⁡x-∫-∞xF⁢t⁢d⁢t⁢=E⁢K.

Dowód.
Załóżmy, że x>0. Wówczas

x-∫-∞xF(t)dt=∫0x(1-F(t))dt-∫-∞0F(t)dt=∫0xP(K>t)dt-∫-∞0F(t)dt.

Dla t≥0 ⁢K>t wtedy i tylko wtedy, gdy K+>t, zatem korzystając ponownie ze stwierdzenia 11 §5.6 [21] otrzymujemy dla x zbiegającego do +∞

∫0xP(K>t)dt=∫0xP(K+>t)dt→∫0+∞P(K+>t)dt=E(K+).

Ponieważ, jak pokazaliśmy w poprzednim lemacie

∫-∞0F⁢t⁢d⁢t=E⁢K-,

to

limx→+∞⁡x-∫-∞xF⁢t⁢d⁢t=E⁢K+-E⁢K-=E⁢K.
Wniosek 14.3
K1≥S⁢S⁢DK2∧K2∈L1⇒E(K1)≥E(K2).
Twierdzenie 14.2

Niech K1 i K2 zmienne losowe o skończonych wartościach oczekiwanych (K1,K2∈L1). Wówczas następujące warunki są równoważne:
1. K1≥S⁢S⁢DK2;
2. Dla każdej niemalejącej i wklęsłej funkcji φ E⁢φ⁢K1≥E⁢φ⁢K2;
3. Istnieją zmienne losowe K1′ i K2′ o tym samym rozkładzie co odpowiednio K1 i K2, takie, że

K1′≥E(K2′|K1′),

tzn. para K1′,K2′ jest nadmartyngałem.

Dowód -patrz [23, Twierdzenie 5.2.8] lub [14, Theorem 2.58].

Wniosek 14.4

Niech K1 i K2 zmienne losowe o skończonych wartościach oczekiwanych (K1,K2∈L1), a h:I→R, I⊂R funkcja niemalejąca i wklęsła taka, że zmienne losowe K1 i K2 prawie na pewno przyjmują wartości z I

PK1∉I=PK2∉I=0.

Wówczas

K1≥S⁢S⁢DK2⟹h(K1)≥S⁢S⁢Dh(K2).

W szczególności dla a,m∈R i a>0

K1≥S⁢S⁢DK2⟺aK1+m≥S⁢S⁢DaK2+m.

Dowód.
Zauważmy, że wzięta ze znakiem przeciwnym część ujemna z funkcji niemalejącej i wklęsłej też jest niemalejąca i wklęsła. Zatem z dominacji stochastycznej, K1≥S⁢S⁢DK2, wynika, że dla każdego x∈R

E⁢-h⁢K1-x-≥E⁢-h⁢K2-x-,

co jest równoważne dominacji stochastycznej, h(K1)≥S⁢S⁢Dh(K2).

Na zakończenie pokażemy, że dominację stochastyczną pierwszego lub drugiego rzędu można stosować wymiennie do oceny wypłat z inwestycji lub zysku lub stóp zwrotu.

Niech K1 i K2 modelują wypłaty z dwóch inwestycji A i B, wymagających tych samych nakładów k, k>0.

C⁢FA,0=C⁢FB,0=-k,⁢⁢⁢C⁢FA,1=K1,⁢⁢⁢C⁢FB,1=K2.

Przez Z i r oznaczamy odpowiednio zysk i stopę zwrotu

Zi=Ki-k,⁢⁢⁢ri=Ki-kk.

Załóżmy, że dystrybuanty K1 i K2 są różne od siebie tzn.

∃t⁢⁢⁢⁢F1⁢t≠F2⁢t.

Wówczas:

Wniosek 14.5

Jeżeli zachodzi choć jeden z poniższych warunków
∙ K1≥F⁢S⁢DK2,
∙ Z1≥F⁢S⁢DZ2,
∙ r1≥F⁢S⁢Dr2,
to racjonalny inwestor wybierze inwestycję A.

Załóżmy ponadto, że wartości oczekiwane E⁢K1 i E⁢K2 są skończone.

Wniosek 14.6

Jeżeli zachodzi choć jeden z poniższych warunków
∙ K1≥S⁢S⁢DK2,
∙ Z1≥S⁢S⁢DZ2,
∙ r1≥S⁢S⁢Dr2,
to racjonalny inwestor wybierze inwestycję A.

14.2. Własności dominacji stochastycznej

Rozważania w tym podrozdziale ograniczymy do zmiennych losowych całkowalnych, tzn. posiadających skończoną wartość oczekiwaną.

Definicja 14.4

Semiwariancją ujemną i dodatnią zmiennej losowej K nazywamy odpowiednio

S⁢V-⁢K=E⁢K-E⁢K-2⁢ i ⁢S⁢V+⁢K=E⁢K-E⁢K+2.

Pierwiastek z semiwariancji nazywamy semiodchyleniem standardowym

σ-⁢K=S⁢V-⁢K,⁢⁢⁢⁢σ+⁢K=S⁢V+⁢K.

Jeśli zmienna losowa K ma rozkład symetryczny, to semiwariancje są sobie równe i wynoszą połowę wariancji

S⁢V-⁢K=S⁢V+⁢K=12⁢V⁢K.

Gdy w definicji wariancji zastąpimy kwadrat przez moduł, to otrzymamy odchylenie przeciętne. Przypomnijmy:

Definicja 14.5

Odchyleniem przeciętnym, semiodchyleniem przeciętnym
ujemnym i semiodchyleniem przeciętnym dodatnim zmiennej losowej K nazywamy odpowiednio

d⁢K=E⁢K-E⁢K,
s⁢d-⁢K=E⁢K-E⁢K-,⁢⁢⁢s⁢d+⁢K=E⁢K-E⁢K+.

Te trzy wielkości są ściśle ze sobą związane.

Lemat 14.3

Dla dowolnej zmiennej losowej K

s⁢d-⁢K=s⁢d+⁢K=12⁢⁢d⁢K.

Dowód. Zauważmy, że

E⁢K-E⁢K=E⁢K-E⁢K++E⁢K-E⁢K-.

Natomiast

E⁢K-E⁢K+-E⁢K-E⁢K-=E⁢K-E⁢K=0.

Zatem

E⁢K-E⁢K+=E⁢K-E⁢K-⁢ i ⁢E⁢K-E⁢K=2⁢E⁢K-E⁢K-.

Przeanalizujemy teraz zależności między parametrami rozkładów wynikające z dominacji stochastycznej pierwszego lub drugiego rzędu.

Lemat 14.4

Jeśli K1 dominuje stochastycznie nad K2, K1≥F⁢S⁢DK2, to
1. E⁢K1≥E⁢K2.
Jeśli ponadto E⁢K1=E⁢K2, to
2. σ-⁢K1≤σ-⁢K2;
3. σ+⁢K1≥σ+⁢K2;
4. d⁢K1=d⁢K2.

Dowód.
Ad 1.
Rozważamy funkcję φ⁢s=s. Jest to funkcja rosnąca, zatem

E⁢K1=E⁢φ⁢K1≥E⁢φ⁢K2=E⁢K2.

W dalszej części dowodu przyjmiemy, że wartości oczekiwane są równe,
E⁢K1=E⁢K2=m.

Ad 2.
Rozważamy funkcję φ⁢s=-s-m-2. Jest to funkcja niemalejąca, zatem

-S⁢V-⁢K1=E⁢φ⁢K1≥E⁢φ⁢K2=-S⁢V-⁢K2.

Ad 3.
Rozważamy funkcję φ⁢s=s-m+2. Jest to funkcja niemalejąca, zatem

S⁢V+⁢K1=E⁢φ⁢K1≥E⁢φ⁢K2=S⁢V+⁢K2.

Ad 4.
Rozważamy funkcje φ1⁢s=s-m+ i φ2⁢s=-s-m-. Obie są funkcjami niemalejącymi, a więc

s⁢d+⁢K1=E⁢φ1⁢K1≥E⁢φ1⁢K2=s⁢d+⁢K2=
=sd-(K2)=-E(φ2(K2))≥-E(φ2(K1))=sd-(K1).

Zatem s⁢d±⁢K1=s⁢d±⁢K2, czyli również d⁢K1=d⁢K2.

Druga dominacja stochastyczna implikuje trochę słabsze warunki.

Lemat 14.5

Jeśli K1 dominuje stochastycznie nad K2, K1≥S⁢S⁢DK2, to
1. E⁢K1≥E⁢K2.
Jeśli ponadto E⁢K1=E⁢K2, to
2. σ-⁢K1≤σ-⁢K2;
3. d⁢K1≤d⁢K2.

Dowód.
Nierówność dla wartości oczekiwanych była pokazana już w poprzednim podrozdziale (wniosek 14.3). Nierówności 2 i 3 wynikają z faktu, że funkcje φ⁢s=-s-m-2 i φ2⁢s=-s-m- wykorzystane do dowodu 2 i 4 w poprzednim lemacie są nie tylko niemalejące, ale i wklęsłe.

Gdy rozkłady są symetryczne, to semiodchylenia standardowe można zastąpić odchyleniem standardowym.

Wniosek 14.7

Jeśli rozkłady K1 i K2 są symetryczne, E⁢K1=E⁢K2 i K1≥F⁢S⁢DK2, to σ⁢K1=σ⁢K2.

Wniosek 14.8

Jeśli rozkłady K1 i K2 są symetryczne, E⁢K1=E⁢K2 i K1≥S⁢S⁢DK2, to σ⁢K1≤σ⁢K2.

W przypadku rozkładów normalnych dominację stochastyczną można całkowicie opisać w terminach wartości oczekiwanej i odchylenia standardowego.

Twierdzenie 14.3

Niech zmienne losowe K1 i K2 mają rozkłady normalne o parametrach

E⁢Ki=mi,⁢⁢⁢σ⁢Ki=σi.

Wówczas

K1≥F⁢S⁢DK2⟺m1≥m2∧σ1=σ2;
K1≥S⁢S⁢DK2⟺m1≥m2∧σ1≤σ2.

Dowód.
Niech F oznacza dystrybuantę rozkładu normalnego standardowego N⁢0,1. Dystrybuanty zmiennych Ki możemy zapisać w następujący sposób

F1⁢t=F⁢t-m1σ1,⁢⁢⁢F2⁢t=F⁢t-m2σ2.
K1≥F⁢S⁢DK2⇔∀tF1(t)≤F2(t)⇔∀tF(t-m1σ1)≤F(t-m2σ2)

Dystrybuanta F jest ściśle rosnąca, zatem

K1≥F⁢S⁢DK2⇔∀tt-m1σ1≤t-m2σ2⇔m1≥m2∧σ1=σ2.

Druga dominacja jest bardziej skomplikowana. Zauważmy, że

∫-∞xFi⁢t⁢d⁢t=∫-∞xF⁢t-miσi⁢d⁢t=∫-∞x-miF⁢tσi⁢d⁢t.

Najpierw pokażemy, że z nierówności

m1≥m2,⁢⁢⁢σ1≤σ2

wynika druga dominacja stochastyczna. Pokażemy, że pochodna po σ jest nieujemna

∂∂⁡σ⁢∫-∞xF⁢tσ⁢d⁢t=∫-∞xF′⁢tσ⁢-tσ2⁢d⁢t=12⁢π⁢∫-∞x-tσ2⁢exp⁡-t22⁢σ2⁢d⁢t=
=12⁢πexp(-t22⁢σ2)|-∞x=12⁢πexp(-x22⁢σ2)>0.

Zatem przy ustalonych m i x zależność od σ jest monotoniczna. A więc

∫-∞xF1⁢t⁢d⁢t=∫-∞x-m1F⁢tσ1⁢d⁢t≤∫-∞x-m1F⁢tσ2⁢d⁢t≤
≤∫-∞x-m2F(tσ2)dt=∫-∞xF2(t)dt.

Dowód implikacji w drugą stronę. Jak pokazaliśmy powyżej, druga dominacja stochastyczna implikuje nierówność wartości oczekiwanych.

K1≥S⁢S⁢DK2⇒m1≥m2.

Rozważmy następującą granicę, gdy x dąży do -∞

g=limx→-∞⁡∫-∞xF2⁢t⁢d⁢t∫-∞xF1⁢t⁢d⁢t.

Stosując dwukrotnie regułę de l'Hospitala, otrzymujemy

g=limx→-∞⁡F2⁢xF1⁢x=limx→-∞⁡F⁢x-m2σ2F⁢x-m1σ1=
=σ1σ2limx→-∞exp(x-m122⁢σ12-x-m222⁢σ22)=
=⁡0 dla σ1>σ20 dla σ1=σ2∧m1<m21 dla σ1=σ2∧m1=m2+∞ dla σ1=σ2∧m1>m2+∞ dla σ1<σ2⁢

Z drugiej dominacji stochastycznej wynika, że g jest nie mniejsze od 1. Zatem przypadek σ1>σ2 można wykluczyć.

Na zakończenie zajmiemy się zmiennymi losowymi o rozkładzie lognormalnym.

Twierdzenie 14.4

Niech K1 i K2 zmienne losowe o rozkładzie lognormalnym,
Ki=eXi, gdzie zmienne losowe Xi mają rozkład normalny o parametrach

E⁢Xi=mi,⁢⁢⁢σ⁢Xi=σi.

Wówczas

K1≥F⁢S⁢DK2⟺m1≥m2∧σ1=σ2;
K1≥S⁢S⁢DK2⟺   0≤σ22-σ12≤2(m1-m2).

Dowód.
Równoważność dla dominacji stochastycznej pierwszego rzędu wynika z faktu, że funkcja wykładnicza jest rosnąca i odwracalna. Zatem z wniosku 14.1 i charakteryzacji dominacji stochastycznej dla rozkładów normalnych (twierdzenie 14.3) otrzymujemy:

K1≥F⁢S⁢DK2⟺X1≥F⁢S⁢DX2⟺m1≥m2∧σ1=σ2.

W przypadku dominacji stochastycznej drugiego rzędu dominacja X1 nad X2 nie jest równoważna dominacji K1 and K2. Prawdziwa jest tylko implikacja w jedną stronę, która wynika z faktu, że Xi=ln⁡Ki, a logarytm naturalny jest funkcją rosnąca i wklęsła. Z wniosku 14.4 i twierdzenia 14.3 otrzymujemy:

K1≥S⁢S⁢DK2⟹X1≥S⁢S⁢DX2⟹m1≥m2∧σ1≤σ2.

Ponadto z dominacji stochastycznej wynika nierowność dla wartości oczekiwanych

K1≥S⁢S⁢DK2⟹E(K1)≥E(K2).

Przypomnimy, że

E⁢Ki=E⁢eXi=1σi⁢2⁢π⁢∫-∞+∞ex⁢exp⁡-x-mi22⁢σ2⁢d⁢x=
=12⁢π∫-∞+∞eσi⁢x+mie-x22dx=
=12⁢π∫-∞+∞exp(-x-σi22+σi22+mi)dx=exp(σi22+mi).

Zatem

E(K1)≥E(K2)⟺σ122+m1≥σ222+m2⟺σ22-σ12≤2(m1-m2).

Co kończy dowód implikacji w prawą stronę.

Pokażemy teraz, że warunki na parametry σi i mi wystarczają, aby zachodziła dominacja stochastyczna rzędu drugiego. Skorzystamy z warunku 3 twierdzenia 14.2. Niech X1^ i X3^ niezależne zmienne losowe o rozkładzie normalnym

X1^∼N⁢m1,σ1,⁢⁢⁢X3^∼N⁢m2-m1,σ22-σ12.

Niech X2^=X1^+X3^, zatem X2^ też ma rozkład normalny

X2^∼N⁢m2,σ2.

Okazuje się, że para exp⁡X1^, exp⁡X2^ jest nadmartyngałem. Otóż z niezależności X3^ od X1^ wynika, że

E(exp(X2^)|exp(X1^))=exp(X1^)E(exp(X3^))=
=exp⁡X1^⁢exp⁡m2-m1+12⁢σ22-σ12.

Ponieważ założyliśmy, że m2-m1+12⁢σ22-σ12≤0, to

E(exp(X2^)|exp(X1^))≤exp(X1^),

czyli

exp(X1^)≥S⁢S⁢Dexp(X2^).

Aby zakończyć dowód, wystarczy zauważyć, że K1 ma taki sam rozkład jak exp⁡X1^, a K2 jak exp⁡X2^.

14.3. Dochód i ryzyko

14.3.1. Oczekiwany dochód i miary ryzyka

Strategie oparte na dominacji stochastycznej wymagają dokładnej znajomości całego rozkładu, co jest:
a) pracochłonne;
b) kosztowne;
c) czasami niewykonalne.
Ponadto prowadzą one do optymalizacji ,,∞-kryterialnej”. Dlatego bardziej popularne są strategie oparte na dwu kryteriach: prognozowany dochód i ryzyko. Maksymalizujemy prognozowany dochód i minimalizujemy ryzyko. Prowadzi to do następującego kryterium wyboru inwestycji.

Niech zmienne losowe R1 i R2 modelują zysk z dwu inwestycji wymagających tych samych nakładów. Załóżmy, że mają one różne prognozy dochodu lub różne miary ryzyka. Oczywistym jest, że jeśli prognozowany dochód dla R1 jest większy lub równy prognozowanemu dochodowi dla R2 i ryzyko dla R1 jest mniejsze lub równe ryzyku dla R2, to inwestor wybierze R1.

Jako prognozę dochodu najczęściej przyjmuje się wartość oczekiwaną E⁢R, rzadziej medianę me⁢R. W obu przypadkach jest to prognoza punktowa zysku. Im większa wartość prognozy, tym inwestycja jest korzystniejsza. Ale R jest przecież zmienną losową i należy uwzględnić, że wynik może być różny od prognozy. Dlatego wprowadza się pojęcie ryzyka. Ma ono w analizie portfelowej dwa znaczenia.
1. Możliwość wystąpienia efektu niezgodnego z przewidywaniami. Nieważne, czy jest to przykra niespodzianka, czy przyjemne zaskoczenie; ważne, że prognoza była niedokładna.
2. Możliwość poniesienia straty. Uwzględniamy tylko przykre niespodzianki.

Najbardziej popularne miary ryzyka to:

∙ dla niezgodności z przewidywaniami (1.).
Odchylenie standardowe i wariancja.

V⁢R=E⁢R-E⁢R2,⁢⁢⁢σ⁢R=V⁢R;

wyznaczamy prognozę błędu prognozy.

∙ dla możliwości straty (2.).
Ujemne semiodchylenie standardowe i ujemna semiwariancja.

S⁢V-⁢R=E⁢R-E⁢R-2,⁢⁢⁢σ-⁢R=S⁢V-⁢R

S⁢V- i σ-, to odpowiedniki odchylenia standardowego i wariancji w przypadku drugiej interpretacji ryzyka.

∙ dla obu interpretacji ryzyka (1. i 2.).
Odchylenie przeciętne i ujemne semiodchylenie przeciętne.

d⁢R=E⁢R-E⁢R,⁢⁢⁢s⁢d-⁢R=E⁢R-E⁢R-.

Ponieważ d⁢R=2⁢s⁢d-⁢R (lemat 14.3) to można je stosować przy obu interpretacjach ryzyka, mierzą one zarówno błąd prognozy, jak i wielkość możliwej straty.

Zauważmy, że w przypadku rozkładu normalnego powyższe miary są równoważne, w szczególności odchylenie standardowe, semiodchylenie standardowe, odchylenie przeciętne i semiodchylenie przeciętne są proporcjonalne. Rzeczywiście, jeśli R ma rozkład normalny o parametrach m i σ, R∼N⁢m,σ2, to (por. ćwiczenie 14.2)

V⁢R=σ2,⁢⁢σ⁢R=σ,⁢⁢S⁢V-⁢R=12⁢σ2,⁢⁢σ-⁢R=22⁢σ,⁢⁢s⁢d-⁢R=σ2⁢π,⁢⁢d⁢R=2π⁢σ.

14.3.2. Model Markowitza

Przyjęcie wartości oczekiwanej jako miary dochodowości, a odchylenia standardowego jako miary ryzyka jest równoważne stwierdzeniu, że inwestor dokonuje wyboru inwestycji zgodnie z relacją (kryterium) Markowitza ([28, 29]).

Definicja 14.6
R1⪰MR2⇔E(R1)≥E(R2)∧σ(R1)≤σ(R2).

Relacja Markowitza jest określona tylko dla zmiennych losowych o skończonych zarówno wartości oczekiwanej, jak i wariancji (R1,R2∈L2). W przypadku zmiennych losowych o rozkładzie normalnym relacja Markowitza jest zgodna z drugą dominacją stochastyczną. Natomiast w przypadku zmiennych losowych o rozkładach w znaczny sposób różniących się od rozkładu normalnego (np. dyskretnych) należy przy jej stosowaniu zachować dużą ostrożność. Zilustrujemy to następującym przykładem.

Przykład
Rozważmy dwie inwestycje, które wymagają takich samych nakładów i rozliczenie, których nastąpi w tym samym czasie. Wiadomo, że wypłata z pierwszej wyniesie 3 tys. zł, a z drugiej z tym samym prawdopodobieństwem (50%) 3 lub 4 tys. zł. Oczywiste jest, że każdy racjonalny inwestor wybierze drugą inwestycję. Niemniej zauważmy, że

E⁢K2=3,5⁢⁢⁢ i ⁢⁢⁢σ2⁢K2=32⁢12+42⁢12-3,52=252-494=0,25.

Zatem σ⁢K2=0,5, podczas gdy

E⁢K1=3,⁢⁢⁢σ⁢K1=0,

co oznacza, że z punktu widzenia kryterium Markowitza inwestycje K1 i K2 są nieporównywalne.

Zauważmy, że relacja Markowitza zachowuje się przy przeskalowaniu.

Lemat 14.6

Niech a,m∈R, a>0, wówczas

R1⪰MR2⇔aR1+m⪰MaR2+m.

Dowód.
Wartość oczekiwana jest liniowa, a odchylenie standardowe dodatnio jednorodne, zatem

E(R1)≥E(R2)⇔aE(R1)+m≥aE(R2)+m⇔E(aR1+m)≥E(aR2+m),
σ(R1)≤σ(R2)⇔aσ(R1)≤aσ(R2)⇔σ(aR1)≤σ(aR2).

Wobec tego

σ⁢a⁢R1+m≤σ⁢a⁢R2+m.

Zatem obie nierówności zostają zachowane przy przeskalowaniu.

Wniosek 14.9

Niech K1,K2 wypłaty, Z1,Z2 zysk, a R1,R2 stopy zwrotu z dwóch inwestycji, które wymagają tych samych nakładów k. Wówczas następujące warunki są równoważne
i. K1⪰MK2,
ii. Z1⪰MZ2,
iii. R1⪰MR2.

Kryterium Markowitza jest powszechnie używane przy planowaniu składu portfela inwestycyjnego.

Założenia modelowe.
Inwestor inwestuje kwotę k, k>0 w portfel inwestycyjny, który może zawierać d papierów wartościowych. Oznaczmy przez ri stopę zwrotu z i-tego papieru, a przez ki kwotę zainwestowaną w ten papier (k1+…⁢kd=k). ki są znane w momencie zawarcia transakcji, a ri modelujemy jako zmienne losowe o skończonej wariancji. Zysk i stopa zwrotu z portfela wynoszą

Z=k1⁢r1+…+kd⁢rd,⁢⁢⁢R=Zk=k1k⁢r1+…+kdk⁢rd.

Oznaczmy przez xi udział i-tego waloru w portfelu

xi=kik.

Wówczas wzór na stopę zwrotu przyjmuje postać

R=x1⁢r1+…+xd⁢rd.

Wartość oczekiwana stopy zwrotu z portfela jest kombinacją liniową stóp zwrotu z poszczególnych papierów

E⁢R=x1⁢E⁢r1+…+xd⁢E⁢rd,

a wariancja kombinacją liniową ich wariancji i kowariancji ([21] §5.6 Twierdzenie 16)

σ2⁢R=x12⁢σ2⁢r1+…+xd2⁢σ2⁢rd+2⁢x1⁢x2⁢⁢c⁢o⁢v⁢r1,r2+…+2⁢xd-1⁢xd⁢⁢c⁢o⁢v⁢rd-1,rd.

Biorąc pod uwagę, że c⁢o⁢v⁢ri,ri=σ2⁢ri i c⁢o⁢v⁢ri,rj=c⁢o⁢v⁢rj,ri, możemy zapisać powyższy wzór jako podwójną sumę

σ2⁢R=∑i=1d∑j=1dxi⁢xj⁢c⁢o⁢v⁢ri,rj,

lub w postaci macierzowej

σ2⁢R=xT⁢C⁢x,⁢⁢ gdzie ⁢⁢⁢x=x1…xd,⁢⁢⁢C=c⁢o⁢v⁢ri,rji,j=1,…,d⁢.

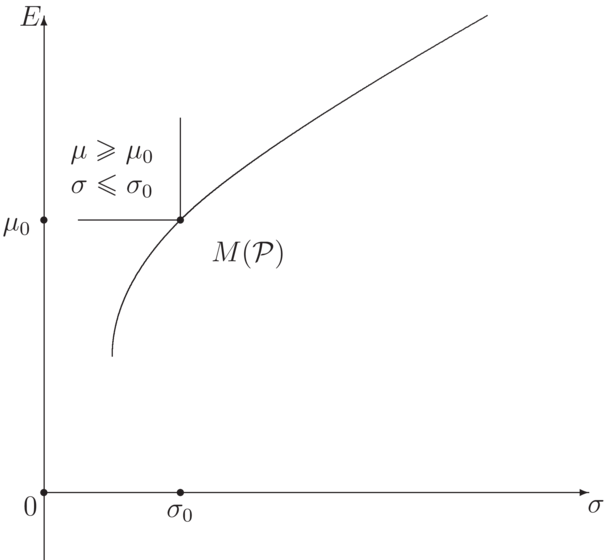
Zbiór inwestycji dopuszczalnych P opisujemy jako podzbiór Rd. Punkt x=x1,…,xd należy do P wtedy i tylko wtedy, gdy inwestor może zainwestować w portfel o składzie x1,…,xd. Na ogół przyjmuje się, że wszystkie aktywa są nieskończenie podzielne i P jest podzbiorem wypukłym hiperpłaszczyzny x1+…+xd=1.

Odwzorowanie, które przyporządkowuje portfelowi o składzie x odchylenie standardowe jego stopy zwrotu σ⁢Rx i jej wartość oczekiwaną E⁢Rx, nazywa się odwzorowaniem Markowitza

M:P→R2,⁢⁢⁢x↦σ⁢Rx,E⁢Rx.

Obraz M⁢P nazywa się zbiorem możliwości. Portfel o składzie x, x∈P, nazywamy efektywnym, gdy stopa zwrotu z tego portfela Rx jest maksymalna względem relacji Markowitza

¬∃y∈PRy≻MRx.

Obraz zbioru portfeli efektywnych jest zawarty w brzegu zbioru możliwości i nazywa się granicą efektywną (rys. 5.2). Zauważmy, że ma ona prostą interpretację geometryczną. Punkt σ0,μ0 należy do granicy efektywnej, gdy zbiór możliwości i zbiór punktów leżących na lewo i powyżej punktu σ0,μ0 przecinają się tylko w tym punkcie

M⁢P∩σ,μ:σ≤σ0∧μ≥μ0=σ0,μ0.
Rys. 14.1. Granica efektywna.

14.4. Ćwiczenia

Ćwiczenie 14.1

Oszacowano następujące prawdopodobieństwa wypłat dla inwestycji A, B i C:

Inwestycja A:

wypłata [tys. zł] 6 8 10 13 15
prawdopodobieństwo [%] 20 10 15 25 30

Inwestycja B:

wypłata [tys. zł] 6 7 9 10 11 14 15 16
prawdopodobieństwo [%] 15 5 5 15 5 25 20 10

Inwestycja C:

wypłata [tys. zł] 6 7 8 9 11 13 14 15
prawdopodobieństwo [%] 10 5 10 5 15 10 25 20

Sprawdzić, czy na podstawie kryterium dominacji stochastycznej można wybrać najlepszą spośród nich (każda wymaga zainwestowania 10 000 zł).

Rozwiązanie.Wypłaty są skokowymi zmiennymi losowymi, zatem ich dystrybuanty (F) są funkcjami schodkowymi, a całki z dystrybuant (G) ciągłymi funkcjami kawałkami liniowymi. Aby je scharakteryzować, wystarczy wyznaczyć ich wartości na dyskretnym zbiorze punktów zawierającym wszystkie wartości, jakie mogą przyjmować z niezerowym prawdopodobieństwem wypłaty KA, KB i KC. Wielkości te są przedstawione w poniższej tabelce.

K 6 7 8 9 10 11 13 14 15 16
A 20 0 10 0 15 0 25 0 30 0
P(K) B 15 5 0 5 15 5 0 25 20 10
C 10 5 10 5 0 15 10 25 20 0
A 20 20 30 30 45 45 70 70 100 100
F B 15 20 20 25 40 45 45 70 90 100
C 10 15 25 30 30 45 55 80 100 100
A 0 20 40 70 100 145 235 305 375 475
G B 0 15 35 55 80 120 210 255 325 415
C 0 10 25 50 80 110 200 255 335 435

Wiersz K zawiera wszystkie możliwe wartości wypłat. W następnych trzech wierszach podane są prawdopodobieństwa, z jakimi są one przyjmowane odpowiednio przez KA, KB i KC. Poniżej są wartości dystrybuant, a pod nimi całek z dystrybuant. Zauważmy, że wartości dystrybuant F i całek G oblicza się rekurencyjnie według następujących wzorów:

F⁢Ki=F⁢Ki-1+pi,⁢⁢⁢G⁢Ki=G⁢Ki-1+F⁢Ki-1⋅Ki-Ki-1.

Na podstawie tabelki stwierdzamy, że w każdym punkcie dystrybuanta FA przyjmuje wartości większe niż dystrybuanta FB bądź równe. Nie jest to prawdą dla pozostałych par dystrybuant FA i FC oraz FB i FC. Zatem KB>F⁢S⁢DKA, a KC jest F⁢S⁢D-nieporównywalne z KB i KA.

Całki G mierzą pola pod wykresami dystrybuant, zatem GA przyjmuje nie mniejsze wartości niż GB. Z tabelki otrzymujemy, że również wykres GC leży poniżej wykresu GA. Natomiast wykresy GB i GC przecinają się. Zatem KB>S⁢S⁢DKA i KC>S⁢S⁢DKA, ale KC jest S⁢S⁢D-nieporównywalne z KB.

Odpowiedź. Inwestor dokonujący wyboru inwestycji na podstawie dominacji stochastycznej pierwszego lub drugiego rzędu powinien odrzucić inwestycję A. Inwestycje B i C są nieporównywalne względem obu dominacji. Zatem kryteria oparte na pierwszej i drugiej dominacji stochastycznej nie dają wskazówek, którą z inwestycji należy wybrać.

Ćwiczenie 14.2

Wyznaczyć ujemne semiodchylenie przeciętne dla zmiennej losowej R o rozkładzie N⁢m,σ2.

Rozwiązanie.

s⁢d-⁢R=E⁢R-m-=-1σ⁢2⁢π⁢∫-∞mx⁢exp⁡-x-m22⁢σ2⁢d⁢x⁢-1σ⁢2⁢π⁢∫-∞0x⁢exp⁡-x22⁢σ2⁢d⁢x=
=σ2⁢πexp(-x22⁢σ2)|0-∞=σ2⁢π.

Odpowiedź. Ujemne semiodchylenie przeciętne dla zmiennej losowej R o rozkładzie N⁢m,σ2 wynosi σ2⁢π.

Ćwiczenie 14.3

W oparciu o relację Markowitza określić, która z poniższych inwestycji jest bardziej, a która mniej korzystna:
inwestycja A – stopa zwrotu ma rozkład N⁢0,1;0,022;
inwestycja B – stopa zwrotu ma rozkład N⁢0,2;0,022;
inwestycja C – stopa zwrotu ma rozkład N⁢0,2;0,032.

Rozwiązanie.Porównujemy wartości oczekiwane i odchylenia standardowe

E⁢RA=0,1<0,2=E⁢RB=E⁢RC,
σ⁢RA=σ⁢RB=0,02<0,03=σ⁢RC.

Zatem inwestycja B ma największą wartość oczekiwaną stopy zwrotu i najmniejsze odchylenie standardowe, czyli

RB≻MRA i RB≻MRC.

Natomiast stopy zwrotu z inwestycji A i C są nieporównywalne względem relacji Markowitza, A ma lepsze odchylenie standardowe, a C wartość oczekiwaną.

Odpowiedź. Zgodnie z relacją Markowitza najkorzystniejsza jest inwestycja B. Pozostałe dwie inwestycje są nieporównywalne względem relacji Markowitza, a tym samym nie daje ona wskazówek, która z nich jest bardziej, a która mniej korzystna.

« 13. Metody stochastyczne w finansach  Spis treści  15. Metody stochastyczne w finansach – cd »  

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

strona główna | webmaster | o portalu | pomoc

© Wydział Matematyki, Informatyki i Mechaniki UW, 2009-2010. Niniejsze materiały są udostępnione bezpłatnie na licencji Creative Commons Uznanie autorstwa-Użycie niekomercyjne-Bez utworów zależnych 3.0 Polska.

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego.

Projekt współfinansowany przez Ministerstwo Nauki i Szkolnictwa Wyższego i przez Uniwersytet Warszawski.