Zagadnienia
3. Struktura terminowa stóp procentowych
Liczba godzin 2.
Zakres materiału:
Wartość pieniądza w czasie. Struktura terminowa stóp procentowych. Stopy spotowe i terminowe. Kontrakty FRA i opcje.
3.1. Wprowadzenie
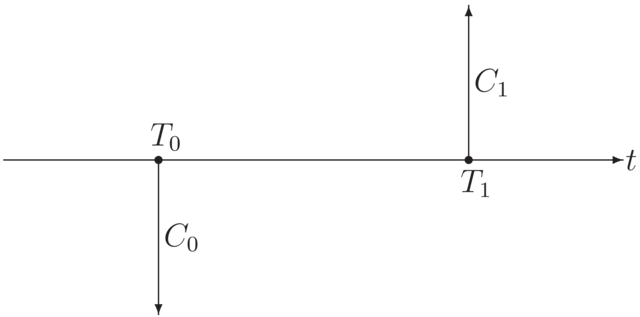
Rozważmy inwestycję o dwu przepływach gotówki
Efektywność takiej inwestycji daje się opisać na kilka sposobów.
Na przykład możemy pytać o
następujące wielkości:
1. Ile kosztuje w chwili
2. Jaka jest (efektywna) stopa zwrotu?
3. Jaka jest (efektywna) intensywność oprocentowania?
Powyższe wielkości są ze sobą powiązane:
Struktura terminowa to
relacja między efektywnością opisanej powyżej inwestycji, a czasem pozostałym do momentu zapadalności.
opisują strukturę terminową stóp zwrotu
(stóp procentowych).
Ich wykresy nazywa się ,,krzywą dochodowości”
lub ,,krzywą zwrotów” (yield curve).
Natomiast
opisuje strukturę terminową czynnika dyskontującego.
Mamy następujące ograniczenia (warunki brzegowe) na funkcję
Ponadto
Rzeczywiście, gdyby dla pewnych
Rynek dostarcza nam informacje tylko o wartościach
Zauważmy, że skoro
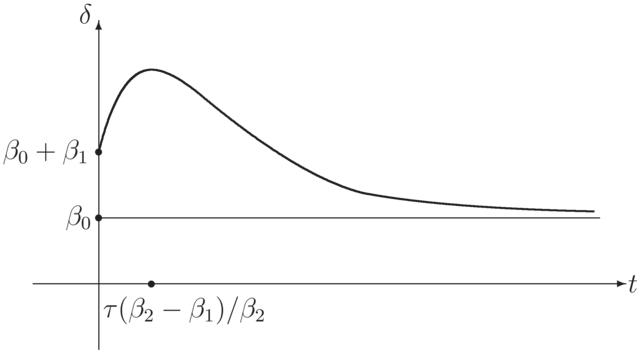
3.2. Interpretacja R ¯ t δ t
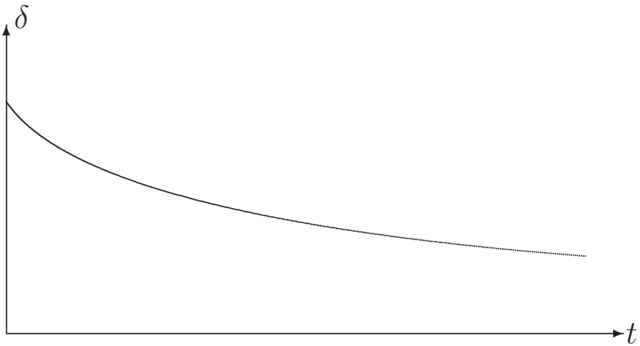
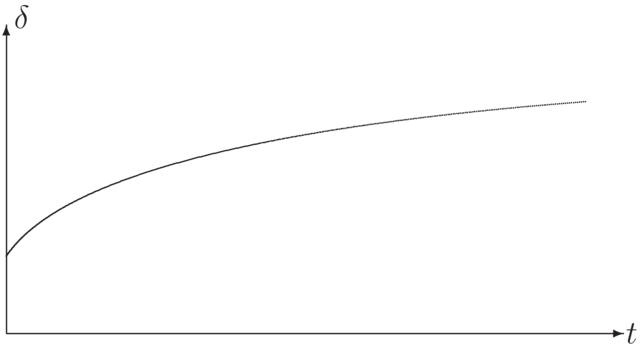
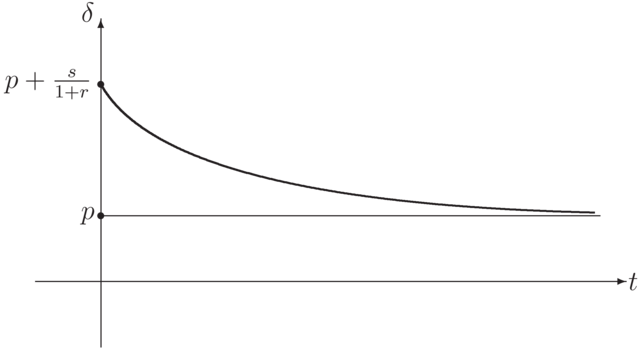
Powyższe rysunki są ilustracją tzw. faktów stylizowanych, tzn. pewnych uproszczeń sytuacji,
z którymi spotykamy się w życiu. Strukturę terminową modelujemy za pomocą rodziny funkcji zależnych od parametrów.
Dobry model powinien opisywać fakty stylizowane.
3.3. Przykłady struktur terminowych
Dla większej czytelności zapisu wprowadzimy nową funkcję
Niektórzy autorzy nazywają ją funkcją dochodowości (yield function).
3.3.1. Struktura terminowa płaska
Zauważmy, że wartości
Lemat 3.1
Jeśli
Dowód.
3.3.2. Struktura terminowa kawałkami płaska
gdzie
Lemat 3.2
Dla
Strukturę kawałkami płaską stosujemy gdy znamy tylko skończoną liczbę wartości
3.3.3. Wzór Stoodleya
Wówczas
Jak widać z powyższego,
Własności funkcji
Funkcja
3.3.4. Wzór Nelsona-Siegela
Wzór Nelsona-Siegela ([24, §15.4]) jest często używany do przybliżonego opisu struktury terminowej.
Wówczas
Zaletą wzoru Nelsona-Siegela jest liniowa zależność
Ponadto
Czyli pochodna
Zatem intensywność
Dla parametru
3.3.5. Wzór Vasička
W tym przypadku wzór na funkcję dochodowości
Po scałkowaniu otrzymujemy
Funkcja
Chwilową intensywność otrzymujemy, różniczkując
Zauważmy, że
Okazuje się, że dobierając odpowiednio parametry,
możemy otrzymać funkcję
Lemat 3.3
Jeżeli
Jeżeli
Jeżeli
Dowód.
Funkcję
Trójmian kwadratowy
Gdy
Interpretacja parametrów modelu:
3.3.6. Wzór CIR
Tym razem wzór na funkcję dochodowości
Po scałkowaniu otrzymujemy
Funkcja
Chwilową intensywność otrzymujemy, różniczkując
Zauważmy, że
Lemat 3.4
Jeżeli
Jeżeli
Jeżeli
Interpretacja parametrów jest identyczna jak w modelu Vasička.
3.4. Instrumenty pochodne
3.4.1. Kontrakty FRA
FRA (ang. Forward Rate Agreement) to umowa pomiędzy dwoma kontrahentami, którzy ustalają wysokość stopy procentowej mającej obowiązywać w przyszłości dla określonej kwoty wyrażonej w walucie transakcji dla z góry ustalonego okresu.
W kontrakcie FRA są dwie strony transakcji:
1. Długa pozycja (ang. long position –- a FRA buyer) otrzymuje przepływ determinowany przez stawkę referencyjną, w zamian za stawkę stałą kontraktu (co niekiedy, w celu uniknięcia popełnienia błędu, bywa zapisywane jako: RECEIVE floating and PAY fixed),
2. Krótka pozycja (ang. short position –- a FRA seller) otrzymuje przepływ stały (którego wysokość w rzeczywistości jest ustalona w dniu zawarcia transakcji) w zamian za stawkę referencyjną (RECEIVE fixed and PAY floating).
W kontrakcie FRA występuje:
1. Data zawarcia transakcji (ang. transaction date)
2. Data ustalenia stawki referencyjnej (ang. fixing date)
3. Data rozpoczęcia okresu odsetkowego obowiązywania stawki referencyjnej (ang. start date)
4. Data zakończenia okresu odsetkowego obowiązywania stawki referencyjnej (ang. end date)
Stopy (stawki)
Rozliczenie kontraktu następuje w drugim kolejnym dniu roboczym po ustaleniu stawki
gdzie
Stawki
Lemat 3.5
Dowód.
Rozważmy dwie inwestycje:
A. Sprzedaż kontraktu FRA na okres
B. Kupno obligacji płacących 1 w chwili
Rozliczenie.
W chwili zawarcia transakcji mamy:
Rozliczenie obu transakcji nastąpi w chwili
Po przyrównaniu obydwu wypłat otrzymujemy
Co po uproszczeniu daje tezę lematu.
3.4.2. Kontrakty IRS
Swap stopy procentowej, IRS (ang. interest rate swap), to kontrakt wymiany płatności odsetkowych, jeden z podstawowych instrumentów pochodnych, będący przedmiotem obrotu na rynku międzybankowym. IRS jest umową pomiędzy dwiema stronami, na podstawie której strony wypłacają sobie wzajemnie (w określonych odstępach czasu w trakcie trwania kontraktu) odsetki od umownego nominału kontraktu, naliczane według odmiennie zdefiniowanych stóp procentowych. Transakcja IRS może być traktowana jako seria kontraktów FRA, albo jako wymiana odsetek od dwóch obligacji kuponowych.
Obecnie w coraz większym zakresie transakcje IRS zawierane są przez korporacje. Dokonują tego m.in. w celu zapewnienia sobie stałego kosztu finansowania (receive floating rate and pay fixed), albo pozyskania tańszego finansowania w walucie obcej (receive foreing fixed rate vs. pay domestic fixed rate).
W rodzinie IRS można wyróżnić:
1. Prosty (waniliowy) swap stopy procentowej (ang. plain vanilla IRS) – strony wymieniają się przepływami uzależnionymi od stopy stałej i zmiennej (fixed rate vs. floating rate).
2. Basis swap - obie strony płacą odsetki wg różnej stopy zmiennej, np. WIBOR 3-miesięczny w zamian za WIBOR 6-miesięczny (floating rate vs. floating rate).
3. Walutowy swap stopy procentowej (ang. currency IRS, CIRS) – strony wymieniają się płatnościami denominowanymi w różnych walutach. Nie należy go mylić ze swapem walutowym.
W waniliowej transakcji IRS wyróżnia się dwie pozycje, przy czym to kierunek płatności stawki zmiennej określa jaką pozycję zajmuje kontrahent w transakcji IRS:
1. Kontrahent A zajmuje długą pozycję w stopie zmiennej – referencyjnej, gdy otrzymuje przepływ wyznaczony przez stawkę zmienną w zamian za ustaloną stawkę stałą (RECEIVE floating and PAY fixed).
2. Kontrahent B zajmuje krótką pozycję w stopie zmiennej (ang. short position), gdy płaci odsetki określone przez stawkę zmienną, a w zamian otrzymuje płatności determinowane przez stawkę stałą (RECEIVE fixed and PAY floating).
W charakterze stopy zmiennej występuje zazwyczaj stopa ”rynkowa” (LIBOR, EURIBOR, WIBOR lub inna, zależnie od rynku). Wysokość stopy stałej dla standardowych kontraktów jest kwotowana przez banki i zwana stopą swapową (ang. swap rate). Jest ona dobrana w taki sposób, by początkowa wartość kontraktu była zerowa.
Należy zwrócić uwagę, że wysokość stopy zmiennej płaconej w danym okresie odsetkowym standardowo ustalana jest z góry na początku tego okresu (tak jak dla lokat bankowych). Niekiedy spotykane są kontrakty, w których stopa ta ustalana jest z dołu (tzw. ang. LIA swap lub Libor in arrears swap). Należą one jednak do grupy skomplikowanych w wycenie, tzw. egzotycznych instrumentów pochodnych.
3.4.3. Opcje na stopę procentową
Opcja na górny pułap stopy procentowej (interest rate cap)
jest instrumentem służącym do ochrony różnego rodzaju zobowiązań głównie długoterminowych przed wzrostem stopy procentowej. Przedmiotem zabezpieczenia mogą być na przykład długoterminowe kredyty lub różnego rodzaju instrumenty finansowe, których oprocentowanie jest zmienne i ustalane na bazie danej stawki referencyjnej. Opcja cap jest wielookresowym odpowiednikiem opcji call. W wyniku zawarcia transakcji cap nabywca opcji otrzymuje gwarancję od sprzedawcy, którym jest najczęściej bank, że wzrost stopy procentowej ponad poziom uzgodniony w umowie zostanie zrekompensowany przez sprzedającego
Opcja na dolny pułap stopy procentowej (interest rate floor)
jest instrumentem służącym do ochrony różnego rodzaju należności długoterminowych (choć nie tylko) przed spadkiem stopy procentowej. Przedmiotem tego zabezpieczenia mogą być długoterminowe lokaty lub różnego rodzaju instrumenty finansowe, których oprocentowanie jest zmienne i ustalane na bazie danej stawki referencyjnej. Opcja floor jest wielookresowym odpowiednikiem opcji put. W wyniku zawarcia transakcji typu floor nabywca opcji otrzymuje od sprzedawcy, którym jest najczęściej bank, gwarancję, że spadek stopy procentowej poniżej uzgodnionego w umowie pułapu zostanie zrekompensowany przez sprzedającego. Kompensata polega na przekazaniu przez wystawcę floor kwoty stanowiącej różnicę pomiędzy referencyjną stopą procentową, a stopą procentową ustaloną w transakcji opcyjnej zwaną pułapem. Wystawca płaci ją na początku każdego podokresu wówczas, gdy różnica pomiędzy powyższymi kwotami jest ujemna. W każdym innym przypadku nie dochodzi do żadnej płatności.
3.5. Ćwiczenia
Ćwiczenie 3.1
Rozważamy strukturę terminową stóp procentowych opisaną przez chwilową intensywność
Inwestor zainwestował 1 JM na okres
Rozwiązanie.
Niech
Ponadto
Odpowiedź. Wypłata jest równa
Ćwiczenie 3.2
Udowodnić lemat 3.4.
Ćwiczenie 3.3
Wyznaczyć stopę
a. dla płaskiej struktury terminowej.
b. dla struktury terminowej opisanej wzorem Stoodleya.
c. dla struktury terminowej opisanej wzorem Nelsona-Siegela.
d. dla struktury terminowej opisanej wzorem Vasička.
Zakładamy, że
Ćwiczenie 3.4
Struktura terminowa jest wyznaczona przez chwilową stopę