Zagadnienia
7. Analiza instrumentów dłużnych – cd
7.1. Wewnętrzna stopa zwrotu
7.1.1. Definicja I R R
Rozważmy ciąg płatności
Dla płaskiej struktury terminowej mamy
lub jeśli zastąpimy stopę procentową
Pytanie: Przy jakiej stałej stopie procentowej
Aby odpowiedzieć na to pytanie, wprowadza się pojęcie wewnętrznej stopy zwrotu.
Definicja 7.1
Wewnętrzną stopą zwrotu –
Natomiast wewnętrzną intensywością nazywamy dodatnią liczbę
Jak łatwo zauważyć, wewnętrzna stopa zwrotu, to taka stopa procentowa, przy której
wartość obecna wpływów z inwestycji jest równa wartości obecnej
nakładów inwestycyjnych. Podobnie wewnętrzna intensywność, to taka intensywność oprocentowania,
przy której
wartość obecna wpływów z inwestycji jest równa wartości obecnej
nakładów inwestycyjnych.
Oczywiście obie te wielkości są związane zależnością
Zilustrujemy definicje na przykładzie.
Przykład 7.1
Rozważmy pięcioletni projekt
inwestycyjny:
| Rok | Nakłady | Przychody | |
| 0 | 5000 | 0 | -5000 |
| 1 | 2000 | 0 | -2000 |
| 2 | 1000 | 2000 | 1000 |
| 3 | 1000 | 3000 | 2000 |
| 4 | 1000 | 4000 | 3000 |
| 5 | 1000 | 5000 | 4000 |
Zgodnie z danymi z tabelki mamy
Jedynym dodatnim miejscem zerowym jest 0,10193. Zatem
7.1.2. Istnienie I R R
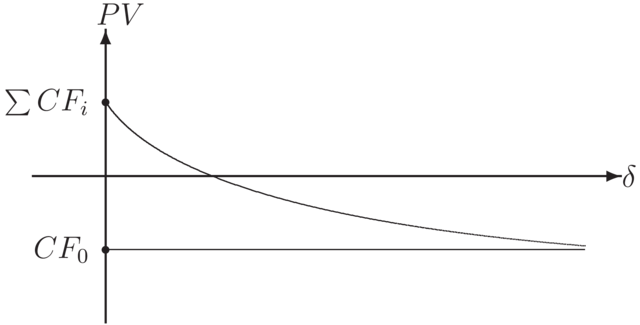
W ogólnym przypadku funkcja
Rozważmy następujący przykład:
Inwestor wpłaca 100 natychmiast i 132 na
koniec dwóch lat w zamian za 230 otrzymane na koniec pierwszego roku.
Równanie wartości dla tej transakcji ma postać
lub
Po sprowadzeniu do postaci iloczynu mamy
Stąd stopą zwrotu jest
Wprawdzie nie jest rzeczą łatwą pogodzić się z faktem, że istnieją
transakcje z wieloma stopami zwrotu, jednak gdy zaobserwujemy, że funkcja
Można sobie wyobrazić przypadki jeszcze bardziej niezwykłe:
Przykład 7.2
Inwestor A może pożyczyć 1000 od inwestora B na rok na 8%
oraz natychmiast zainwestować tę kwotę na rok na 10%. Jaka jest stopa
zwrotu inwestora A?
Odpowiedź. Zysk inwestora A w ciągu roku wynosi 20, ale kwota, którą zainwestował rzeczywiście A, wynosi 0. Tak więc jego stopa zwrotu jest nieskończona.
Przykład 7.3
Jaka jest stopa zwrotu z transakcji, w której inwestor płaci
100 natychmiast oraz 101 na końcu dwóch lat
w zamian za 200 otrzymane na koniec roku?
Odpowiedź. Równaniem wartości jest
co oznacza, że
W tym przypadku wewnętrzna stopa zwrotu nie istnieje.
Pokażemy, że dla w miarę naturalnych ograniczeń na przepływy gotówki
Lemat 7.1
Jeżeli
Dowód.
Rozważmy funkcję
Funkcja
Teza lematu pozostanie prawdziwa, gdy pierwszy przepływ gotówki (wpłata) ma miejsce w momencie
Lemat 7.2
Jeżeli
Dowód patrz ćwiczenie 7.1
7.1.3. Jednoznaczność I R R
Warunki gwarantujące jednoznaczność nie są już tak oczywiste. Najprostszy przypadek to ,,najpierw wpłaty, a potem wypłaty”. W szczególności obejmuje to przypadek inwestycji w obligacje, kiedy mamy jedną wpłatę, a następnie same wypłaty.
Lemat 7.3
Jeżeli
Dowód.
Niech
Wyłączamy czynnik wykładniczy
Następnie rozkładamy sumę na część dodatnią i ujemną. Zauważmy, że funkcja
jest ściśle malejąca. Rzeczywiście dla
Również funkcja
jest ściśle malejąca. Rzeczywiście dla
Zatem funkcja
Ponieważ czynnik wykładniczy nigdzie się nie zeruje, to istnieje dokładnie jedno miejsce zerowe funkcji
Powyższy lemat można uogólnić na przypadek, gdy pierwsza wpłata następuje po czasie
Lemat 7.4
Jeżeli
Bardziej skomplikowany przypadek to ,,jedna zmiana znaku skumulowanego przepływu”.
Oznaczmy przez
Lemat 7.5
Jeżeli
Dowód.
Niech
Zaczniemy od dowodu pomocniczego faktu.
Zatem, gdy
to
Dalej powtarzamy rozumownie z poprzedniego lematu i pokazujemy, że istnieje dokładnie jedna
7.1.4. Kryterium inwestycyjne oparte na I R R
Załóżmy, że istnieje dokładnie jedna
Lemat 7.6
Jeżeli
Dowód.
Uwaga. Gdy
Gdy
Jeżeli
Przykład 7.4
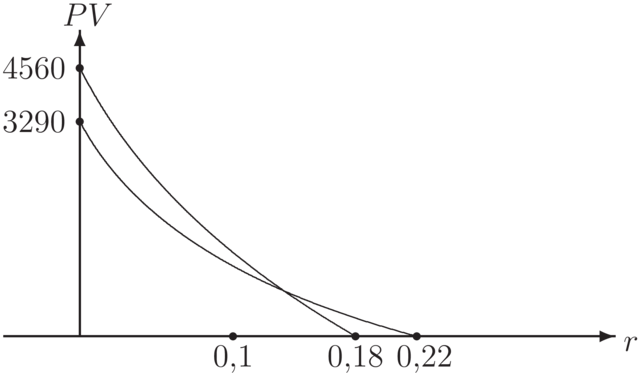
Rozważmy dwa wykluczające się projekty. W projekcie A nakłady
inwestycyjne wynoszą 7000 zł, natomiast wpływy 3430 zł, płatne na koniec każdego
z trzech lat. W projekcie B nakłady inwestycyjne wynoszą 12000 zł, a wpływy 5520 zł,
płatne na koniec każdego z trzech lat. Przy założeniu, że koszt
kapitału wynosi 10% rocznie (rynkowa stopa procentowa),
stosując kryterium PV oraz
Rozwiązanie.
Dla projektu A mamy
7.1.5. I R R Y T M
Rozważmy obligację, z której
Dla takiej obligacji stopa zwrotu liczona do momentu zapadalności (
Lub po podzieleniu przez
To samo równanie wyznacza wewnętrzną stopę zwrotu.
Wniosek 7.1
Ponadto spełnione są założenia lematu 2.2.3. Zatem
7.1.6. Rzeczywista roczna stopa oprocentowania
Wewnętrzna stopa zwrotu znalazła swoje miejsce w obowiązujących w Polsce aktach prawnych
dotyczących kredytów. W ustawie o kredycie konsumenckim ([45, 46])
ustawodawca wprowadził wymóg informowania kredytobiorcy o
,,rzeczywistej rocznej stopie oprocentowania”, którą dla kredytów o stałym
oprocentowaniu wyznacza się jako wewnętrzną stopę
zwrotu dla wszystkich przepływów gotówki wynikających z danej umowy kredytowej.
Zatem jest to stopa procentowa
gdzie,
Transze kredytu (
Zgodnie z ustawą, rzeczywistą roczną stopę oprocentowania podaje się z dokładnością co najmniej do 1 promila.
7.1.7. Uogólnienia
1. Przypadek nieskończonej liczby płatności.
Równanie wartości ma postać
Zadanie jest dobrze postawione, gdy szereg jest zbieżny.
2. Przypadek ciągłego strumienia płatności.
Równanie wartości ma postać
gdzie:
Oznaczmy przez
Lemat 7.7
Jeżeli
Dowód.
Rozważmy funkcję
Jak łatwo zauważyć, zmienia ona znak
Po scałkowaniu przez części otrzymamy
Ponieważ obie otrzymane całki są funkcjami malejącymi zmiennej
7.2. Ćwiczenia
Ćwiczenie 7.1
Udowodnić lemat 7.2.
Rozwiązanie.
Mamy
Oznaczmy drugi czynnik przez
Ponieważ
Funkcja
Ćwiczenie 7.2
Udowodnić lemat 7.4.
Ćwiczenie 7.3
Zainwestowane 200 zł zwracają 120 zł po roku i 110 zł po dwóch latach. Wyznaczyć wewnętrzną stopę zwrotu dla tej inwestycji.
Rozwiązanie.
Równanie wartości ma postać
Skracamy współczynniki przez 10, podstawiamy
Czyli
Odpowiedź.
Wewnętrzna stopa zwrotu rozpatrywanej inwestycji wynosi 10%.
Ćwiczenie 7.4
Która z poniższych inwestycji ma wyższą wewnętrzną stopę zwrotu?
Inwestycja A.
Zakup za 900 zł czteroletniej kuponowej obligacji o wartości nominalnej 1 000 zł
o stałym rocznym oprocentowaniu 20% (odsetki płatne po upływie kolejnego roku).
Inwestycja B.
Zakup za 800 zł zerokuponowej rocznej obligacji o wartości nominalnej 1 000 zł.
Rozwiązanie.
Wewnętrzna stopa zwrotu dla zerokuponowej rocznej obligacji o wartości nominalnej 1 000 zł i cenie 800 zł jest równa ,,zwykłej” stopie zwrotu i wynosi
Wyznaczamy Present Value inwestycji A dla
Ponieważ
Odpowiedź.
Inwestycja B ma wyższą wewnętrzną stopę zwrotu.
Ćwiczenie 7.5
Kredytobiorca otrzymał kredyt 10 tys. zł wypłacony w dwóch równych transzach w odstępie rocznym.
W kolejnych latach kredytobiorca spłacił kredyt w czterech równych ratach po 3000 zł.
Spłaty miały miejsce po dwóch, trzech, czterech i pięciu latach od dnia
wypłaty pierwszej transzy. Ponadto przy wypłacie pierwszej transzy pobrano prowizję
w wysokości 500 zł. Ile wyniosła rzeczywista roczna stopa oprocentowania?
Rozwiązanie.
Mamy sześć przepływów gotówki
Z lematu 2.2.3 wynika, że dla powyższych przepływów gotówki wewnętrzna stopa zwrotu,
a więc i rzeczywista roczna stopa oprocentowania
Po jego rozwiązaniu otrzymujemy
Odpowiedź.
Rzeczywista roczna stopa oprocentowania wynosi 8,3%.
Ćwiczenie 7.6
Sklep z artykułami gospodarstwa domowego proponuje swoim klientom ,,kredyt 0%”.
Należność za nabyty towar klient płaci w 12 równych miesięcznych ratach.
Ponadto za udzielenie kredytu pobierana jest prowizja, która wynosi 5% kwoty kredytu.
Wiedząc, że pierwsza rata ma miejsce po miesiącu od zawarcia umowy kredytowej (i zakupu towaru), a prowizja
jest pobierana w dniu zawarcia umowy, wyznacz rzeczywistą roczną stopę oprocentowania.
Rozwiązanie.
Mamy trzynaście przepływów gotówki
Zatem rzeczywista roczna stopa oprocentowania
Po jego rozwiązaniu otrzymujemy
Odpowiedź.
Rzeczywista roczna stopa oprocentowania wynosi 10%.
Ćwiczenie 7.7
Inwestor zakupił za 100 JM rentę o ciągłym stałym strumieniu płatności o gęstości 10 w skali roku. Płatności zaczną się za rok i będą trwały nieprzerwanie 11 lat. Wyznaczyć wewnętrzną stopę zwrotu.
Rozwiązanie.
Równanie wartości ma postać
Jego pierwiastek to
Zatem
Odpowiedź.
Wewnętrzna intensywnośc wynosi 0,0148, a wewnętrzna stopa zwrotu 0,0149.