Zagadnienia
3. Centralne Twierdzenie Graniczne
Centralne twierdzenie graniczne dotyczy zachowania się rozkładu sum niezależnych zmiennych losowych, przy odpowiedniej normalizacji i pewnych dodatkowych założeniach. Intuicyjnie, suma dużej liczby ,,małych”, niezależnych zmiennych losowych ma rozkład normalny. Główny wynik niniejszego rozdziału jest następujący.
Twierdzenie 3.1 (Lindeberg)
Załóżmy, że dla każdego ![]() , zmienne
, zmienne ![]() ,
, ![]() ,
, ![]() ,
, ![]() są niezależnymi zmiennymi losowymi o średniej
są niezależnymi zmiennymi losowymi o średniej ![]() , takimi, że
, takimi, że
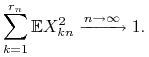 |
Dodatkowo, załóżmy, że jest spełniony warunek Lindeberga
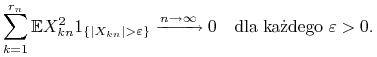 |
(L) |
Wówczas ![]()
Powstaje tu naturalne pytanie, co tak naprawdę mówi warunek Lindeberga. Intuicyjnie rzecz biorąc, oznacza on, iż przy ![]() zbiegającym do nieskończoności,
zmienne
zbiegającym do nieskończoności,
zmienne ![]() ,
, ![]() ,
, ![]() ,
, ![]() są
,,równie małe”. Innymi słowy, w
są
,,równie małe”. Innymi słowy, w ![]() -tym wierszu nie ma zmiennych losowych, które byłyby dominujące w stosunku do pozostałych. Ściślej, mamy następujące
dwie własności.
-tym wierszu nie ma zmiennych losowych, które byłyby dominujące w stosunku do pozostałych. Ściślej, mamy następujące
dwie własności.
Wnioski z warunku Lindeberga
1. Mamy ![]() . Istotnie, dla każdego
. Istotnie, dla każdego ![]() ,
,
2. Mamy ![]() . Rzeczywiście, dla dowolnego
. Rzeczywiście, dla dowolnego ![]() ,
,
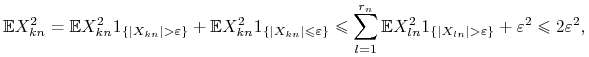 |
o ile ![]() jest dostatecznie duże.
jest dostatecznie duże.
Sformułujmy teraz nieco inną wersję CTG.
Twierdzenie 3.2
Załóżmy, że ![]() są niezależnymi zmiennymi losowymi całkowalnymi z kwadratem,
są niezależnymi zmiennymi losowymi całkowalnymi z kwadratem, ![]() ,
, ![]() Var
Var![]() ,
, ![]() . Jeśli jest spełniony warunek Lindeberga
. Jeśli jest spełniony warunek Lindeberga
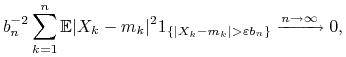 |
(L) |
to
Wynika to bezpośrednio z twierdzenia Lindeberga, przy ![]() ,
, ![]()
Powstaje naturalne pytanie: kiedy warunek Lindeberga jest spełniony? Podamy tu kilka własności wymuszających ten warunek.
Stwierdzenie 3.1
Załóżmy, że ![]() ,
, ![]() ,
, ![]() są niezależne i mają ten sam rozkład o dodatniej wariancji. Oznaczmy
są niezależne i mają ten sam rozkład o dodatniej wariancji. Oznaczmy ![]() ,
, ![]() Var
Var![]() . Wówczas warunek Lindeberga jest spełniony i
. Wówczas warunek Lindeberga jest spełniony i
Dowód:
Wystarczy sprawdzić warunek Lindeberga. Mamy
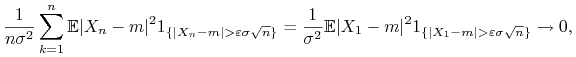 |
na mocy twierdzenia Lebesgue'a.
∎Sprawdzenie dwóch poniższych warunków pozostawiamy jako ćwiczenie.
Stwierdzenie 3.2
Załóżmy, że ![]() są wspólnie ograniczonymi niezależnymi zmiennymi losowymi spełniającymi warunek
są wspólnie ograniczonymi niezależnymi zmiennymi losowymi spełniającymi warunek ![]() Var
Var![]() . Wówczas spełniony jest warunek Lindeberga.
. Wówczas spełniony jest warunek Lindeberga.
Stwierdzenie 3.3 (Lapunow)
Załóżmy, że dla każdego ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() są niezależnymi, scentrowanymi zmiennymi losowymi spełniającymi warunki
są niezależnymi, scentrowanymi zmiennymi losowymi spełniającymi warunki
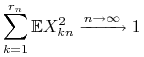 |
oraz
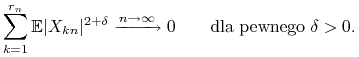 |
Wówczas jest spełniony warunek Lindeberga.
Przechodzimy do dowodu twierdzenia Lindeberga.
Lemat 3.1
Załóżmy, że ![]() ,
, ![]() są liczbami zespolonymi, z których każda ma moduł niewiększy niż
są liczbami zespolonymi, z których każda ma moduł niewiększy niż ![]() . Wówczas
. Wówczas
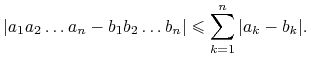 |
Dowód:
Stosujemy indukcję. Dla ![]() nierówność jest oczywista. Dalej, załóżmy, że jest ona prawdziwa dla pewnego
nierówność jest oczywista. Dalej, załóżmy, że jest ona prawdziwa dla pewnego ![]() spróbujmy ją udowodnić dla
spróbujmy ją udowodnić dla ![]() . Oznaczając
. Oznaczając ![]() ,
, ![]() , mamy
, mamy
co kończy dowód.
∎Lemat 3.2
Dla dowolnego ![]() oraz
oraz ![]() mamy
mamy
Dowód:
Stosujemy indukcję. Dla ![]() mamy
mamy
Dalej, załóżmy, że nierówność zachodzi dla pewnego ![]() . Wówczas
. Wówczas
Dowód jest zakończony.
∎Dowód twierdzenia Lindeberga:
Oznaczmy ![]() ,
, ![]() ,
, ![]() . Na mocy twierdzenia Levy-Cramera wystarczy udowodnić, że dla każdego
. Na mocy twierdzenia Levy-Cramera wystarczy udowodnić, że dla każdego ![]() ,
, ![]() Ustalmy więc
Ustalmy więc ![]() . Mamy
. Mamy
Stosujemy teraz pierwszy z powyższych lematów oraz fakt, iż ![]() , gdzie
, gdzie ![]() . W konsekwencji,
. W konsekwencji,
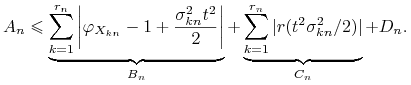 |
Wystarczy wykazać, że ![]() dążą do
dążą do ![]() . Zbieżność ciągu
. Zbieżność ciągu ![]() do
do ![]() jest oczywista na mocy warunku
jest oczywista na mocy warunku ![]() . Zajmijmy się teraz ciągiem
. Zajmijmy się teraz ciągiem ![]() . Ustalmy
. Ustalmy ![]() . Istnieje
. Istnieje ![]() taka,że jeśli
taka,że jeśli ![]() , to
, to ![]() . Jak już wiemy, warunek Lindeberga pociąga za sobą, iż dla dostatecznie dużych
. Jak już wiemy, warunek Lindeberga pociąga za sobą, iż dla dostatecznie dużych ![]() ,
, ![]() , a co za tym idzie,
, a co za tym idzie,
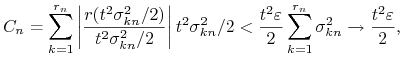 |
a więc ciąg ![]() zbiega do
zbiega do ![]() . Wreszcie, dla ustalonego
. Wreszcie, dla ustalonego ![]() , korzystając z drugiego z powyższych lematów (z
, korzystając z drugiego z powyższych lematów (z ![]() oraz z
oraz z ![]() ),
),
Zatem
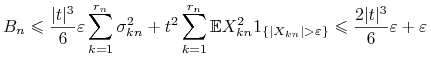 |
dla dostatecznie dużych ![]() . Stąd teza.
. Stąd teza.
Jako wniosek, otrzymujemy
Twierdzenie 3.3 (de Moivre'a-Laplace'a)
Załóżmy, że ![]() ma rozkład Bernoulliego z parametrami
ma rozkład Bernoulliego z parametrami ![]() ,
, ![]() . Wówczas
. Wówczas
Dowód:
Niech ![]() będą niezależnymi zmiennymi losowymi o tym samym rozkładzie dwupunktowym
będą niezależnymi zmiennymi losowymi o tym samym rozkładzie dwupunktowym ![]()
![]() . Mamy
. Mamy
i wystarczy skorzystać z odpowiedniej wersji CTG.
∎Sformułujmy teraz uogólnienie twierdzenia Lindeberga. Dowodzi się je w sposób analogiczny.
Twierdzenie 3.4
Załóżmy, że dla każdego ![]() zmienne
zmienne ![]() ,
, ![]() ,
, ![]() ,
, ![]() są niezależne i całkowalne z kwadratem. Oznaczmy
są niezależne i całkowalne z kwadratem. Oznaczmy ![]() i przypuśćmy, że
i przypuśćmy, że
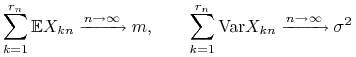 |
oraz
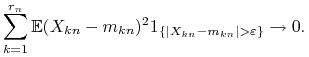 |
(L) |
Wówczas ![]()
Centralne twierdzenie graniczne pozwala badać zachowanie dystrybuant sum niezależnych zmiennych losowych. Istotnie, zbieżność
jest równoważna zbieżności punktowej dystrybuant:
Co więcej, zbieżność jest jednostajna względem ![]() (por. zadanie 9 z rozdziału o słabej zbieżności). Zatem dla każdego
(por. zadanie 9 z rozdziału o słabej zbieżności). Zatem dla każdego ![]() istnieje numer
istnieje numer ![]() taki, że dla
taki, że dla ![]() ,
,
czyli
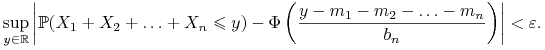 |
Powstaje naturalne pytanie w jaki sposób wyznaczać ![]() w zależności od
w zależności od ![]() ; innymi słowy, w jaki sposób szacować błąd związany z przybliżeniem dysrtybuanty sumy przez dystrybuantę standardowego rozkładu normalnego.
; innymi słowy, w jaki sposób szacować błąd związany z przybliżeniem dysrtybuanty sumy przez dystrybuantę standardowego rozkładu normalnego.
Twierdzenie 3.5 (Nierówność Berry-Essena)
Załóżmy, że ![]() ,
, ![]() ,
, ![]() , są niezależnymi scentrowanymi zmiennymi losowymi o tym samym rozkładzie i niech
, są niezależnymi scentrowanymi zmiennymi losowymi o tym samym rozkładzie i niech ![]() Var
Var![]() ,
, ![]() . Wówczas
. Wówczas
gdzie jako ![]() można wziąć
można wziąć ![]() (optymalna - czyli najmniejsza możliwa - wartość
(optymalna - czyli najmniejsza możliwa - wartość ![]() nie jest znana).
nie jest znana).
W szczególności, przy założeniach twierdzenia de Moivre'a-Laplace'a,
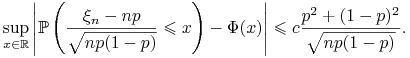 |
Jest to niezwykle użyteczny rezultat z punktu widzenia konkretnych zastosowań: w sposób jawny określa on tempo zbieżności.
3.1. Zadania
1. Sumujemy ![]() liczb, każdą zaokrągloną z dokładnością do
liczb, każdą zaokrągloną z dokładnością do ![]() . Przypuśćmy, że błędy spowodowane przez zaokrąglenia są niezależnymi zmiennymi losowymi o rozkładzie jednostajnym na przedziale
. Przypuśćmy, że błędy spowodowane przez zaokrąglenia są niezależnymi zmiennymi losowymi o rozkładzie jednostajnym na przedziale ![]() . Znaleźć przedział (możliwie krótki), do którego z prawdopodobieństwem
. Znaleźć przedział (możliwie krótki), do którego z prawdopodobieństwem ![]() będzie należał błąd całkowity (tzn. po zsumowaniu).
będzie należał błąd całkowity (tzn. po zsumowaniu).
2. Obliczyć
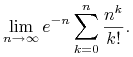 |
3. Udowodnić Stwierdzenie 10 oraz Stwierdzenie 11.
4. Dany jest ciąg ![]() niezależnych zmiennych losowych, przy czym dla
niezależnych zmiennych losowych, przy czym dla ![]() ,
,
Udowodnić, że
mimo iż ![]() Var
Var![]() .
.
5. Zmienne losowe ![]() są niezależne, przy czym dla
są niezależne, przy czym dla ![]() ,
,
![]() . Niech
. Niech ![]() .
Czy ciąg zmiennych losowych
.
Czy ciąg zmiennych losowych
jest zbieżny wedlug rozkładu, a jeśli tak, to do jakiej
granicy?
6. Załóżmy, że ![]() jest zmienną losową spełniającą warunki
jest zmienną losową spełniającą warunki
(i) ![]() ,
,
(ii) Jeśli ![]() ,
, ![]() są niezależne i mają ten sam rozkład co
są niezależne i mają ten sam rozkład co ![]() , to
, to ![]() .
.
Wykazać, że ![]() ma rozkład Gaussa o średniej
ma rozkład Gaussa o średniej ![]() .
.
7. Rzucono ![]() razy kostką. Sumujemy oddzielnie parzyste
liczby oczek i nieparzyste liczby oczek. Jakie jest przybliżone
prawdopodobieństwo tego, że suma parzystych liczb oczek będzie o co
najmniej
razy kostką. Sumujemy oddzielnie parzyste
liczby oczek i nieparzyste liczby oczek. Jakie jest przybliżone
prawdopodobieństwo tego, że suma parzystych liczb oczek będzie o co
najmniej ![]() większa od sumy nieparzystych liczb oczek?
większa od sumy nieparzystych liczb oczek?
8. Liczba studentów przyjętych na pierwszy rok jest zmienną
losową o rozkładzie Poissona z parametrem 100. Jeśli ta liczba
przekroczy 120, tworzy się 2 grupy wykładowe. Obliczyć przybliżone
prawdopodobieństwo (korzystając z CTG), że nie trzeba będzie
tworzyć dwóch grup.
9. Dane są dwa ciągi ![]() ,
, ![]() niezależnych zmiennych
losowych, przy czym zmienne
niezależnych zmiennych
losowych, przy czym zmienne ![]() mają ten sam
rozkład wykładniczy z parametrem
mają ten sam
rozkład wykładniczy z parametrem ![]() , a
, a ![]() mają rozkład
Poissona z parametrem
mają rozkład
Poissona z parametrem ![]() . Zbadać zbieżność według rozkładu ciągu
. Zbadać zbieżność według rozkładu ciągu




