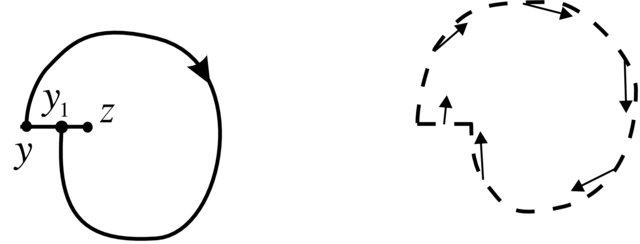Zagadnienia
2. Portrety fazowe autonomicznych pól wektorowych
Definicja 2.1.Portret fazowy autonomicznego pola
wektorowego
Krzywe fazowe są trzech typów:
(i) punkty równowagi, czyli zdegenerowane krzywe odpowiadające stałym rozwiązaniom;
(ii) włożone odcinki (ograniczone lub nieograniczone), czyli
obrazy
(iii) zamknięte krzywe fazowe (włożone okręgi), odpowiadające okresowym rozwiązaniom
| (2.1) |
gdzie
W całym tym rozdziale rozważamy tylko autonomiczne pola wektorowe; dlatego też będziemy opuszczali przmiotnik `autonomiczne'.
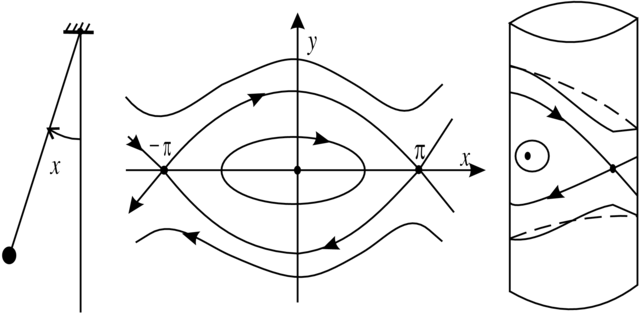
Przykład 2.2 (Wahadło Matematyczne). Jest to następujący układ
na przestrzeni fazowej
Łatwo sprawdzić, że funkcja
| (2.2) |
jest całką pierwszą tego układu, tj.
–punkt
–punkt
–
Łatwo też sprawdzić, że oprócz wskazanych wyżej punktów równowagi mamy dwie krzywe fazowe typu (ii); są to
separatrysy siodła
Możemy policzyć okresy powyższych rozwiązań okresowych leżących na poziomicy
gdzie
Niestety, powyższe całki nie dają się policzyć w terminach
elementarnych funkcji. Rzeczywiście, po podstawieniu
Całka po prawej stronie ostatniej równości to tzw. całka eliptyczna definiująca pewną funkcję eliptyczną6Całki i funkcje eliptyczne pojawiają się bardzo często w równaniach różniczkowych mechaniki klasycznej (patrz [4]. (Zadanie 2.44).
Zauważmy jeszcze, że zamknięte krzywe fazowe w tym przykładzie są nieizolowane, występują w całych rodzinach.
2.1. Rozwiązania okresowe
Zamknięte krzywe fazowe są też nazywane trajektoriami okresowymi lub orbitami okresowymi. W Przykładzie 2.2 występują one w całych rodzinach, ale istnieją też trajektorie okresowe izolowane.
Definicja 2.3.Cyklem granicznym autonomicznego pola wektorowego nazywamy izolowaną zamkniętą krzywą fazową tego pola.
Punkt równowagi takiego pola, który jest otoczony nieizolowanymi zamkniętymi krzywymi fazowymi, nazywa się centrum.
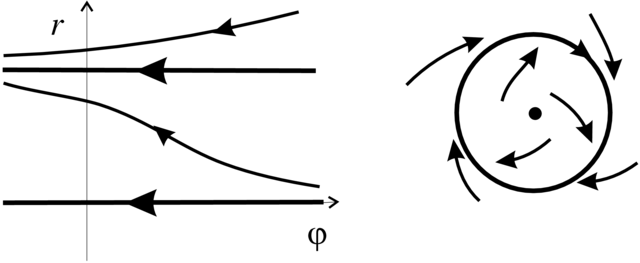
Przykład 2.4. Rozważmy układ
Wygodnie jest badać ten układ w biegunowym układzie współrzędnych
(Zadanie 2.46). Widać, że rozwiązania startujące z
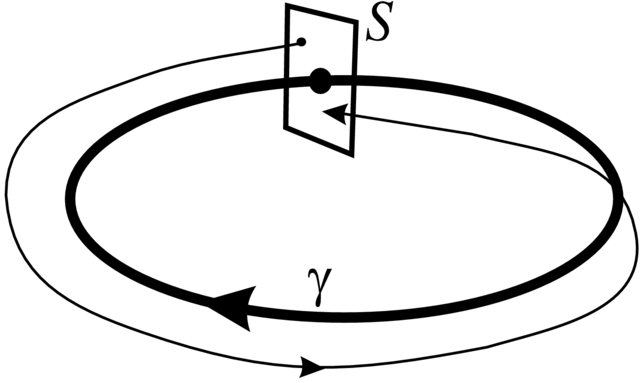
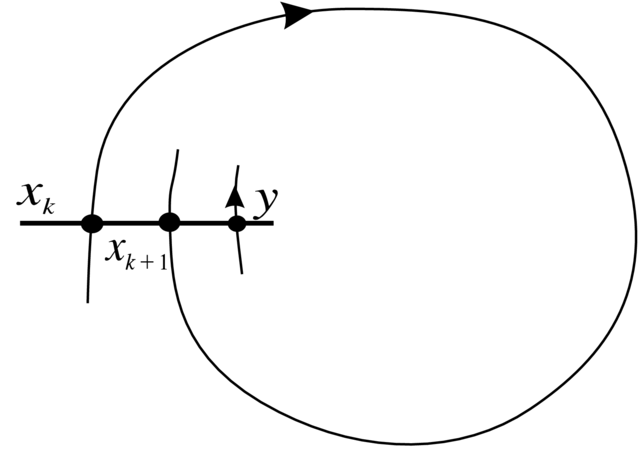
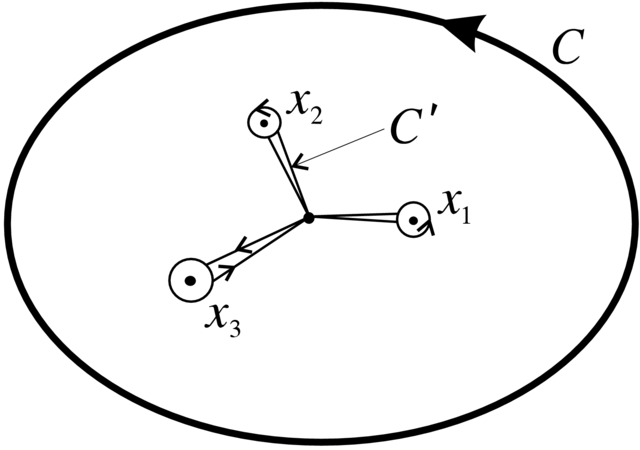
Definicja 2.5. Niech
nazywa się przekształceniem powrotu Poincarégo (patrz Rysunek 2.3).
W tej definicji występuje znaczna dowolność związana z
wyborem cięcia
Lemat 2.6.Dyfeomorfizmy
Dowód. Niech
Cięcie
(Zadanie 2.47).
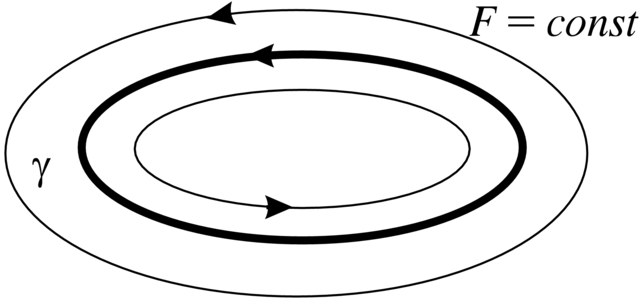
Definicja 2.7. Zamknięta krzywa fazowa
Następujące dwa stwierdzenia są prostymi analogami Twierdzenia Lapunowa i Twierdzenia Hadamarda–Perrona.
Stwierdzenie 2.8.Jeśli
Stwierdzenie 2.9.Jeśli krzywa
Bardziej interesujące chyba jest następujące
Stwierdzenie 2.10.Gdy
Dowód. W istocie tutaj trzeba udowodnić, że rozwiązania okresowe pola
W przypadku
To stwierdzenie ma analog dla punktu osobliwego
| (2.3) |
Stwierdzenie 2.11.W przypadku analitycznego pola typu
(2.3) na płaszczyźnie zachodzi jedna z dwóch możliwości:
albo punkt
Dowód. Trzeba przejść do biegunowego układu współrzędnych
| (2.4) |
gdzie
| (2.5) |
Jego rozwiązania
które jest analogiem przekształcenia powrotu Poincarégo. W istocie
jest to przekształcenie powrotu dla pola (2.3) z półosi
Punkty stałe dyfeomorfizmu
Przekształcenie powrotu Poincarégo
| (2.6) |
Łatwo sprawdzić, że
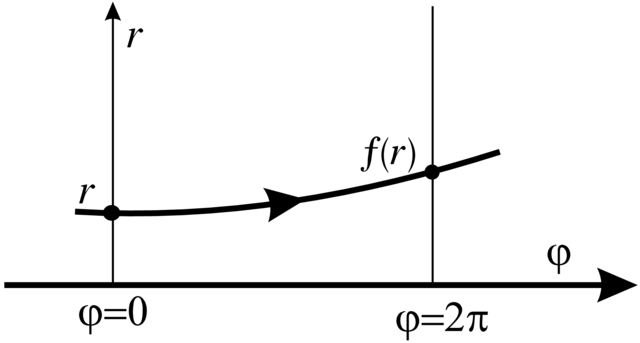
Lemat 2.12.Jeśli
Ten lemat jest konsekwencją Twierdzenia Poincarégo–Dulaca
(dowodzonego w Rozdziale 3.3.1) i dlatego go tutaj nie dowodzimy. Słuchacze mogą dowodzić go wykorzystując pewne własności
symetrii (względem zamiany
Stąd wynika, że jeśli
Definicja 2.13. Wspólczynniki
nazywają się liczbami ogniskowymi Lapunowa–Poincarégo.
Uwaga 2.14. Liczby ogniskowe są ważnie przy badaniu tzw. małych cykli granicznych, tzn. które rodzą się z ogniska w przypadku, gdy pole wektorowe zależy od pewnych parametrów. Jednak są one trudne do policzenia. Poniżej podaję pewien sposób ich wyliczenia; ten sposób w istocie był wykorzystywany przez Lapunowa.
Zamiast współrzędnych rzeczywistych będziemy używać współrzędnych zespolonych
| (2.7) |
gdzie
Będziemy poszukiwać całki pierwszej dla równania (2.7) w postaci
| (2.8) |
gdzie warunek rzeczywistości
Oczekiwana własność
dla współczynników wielomianu
Widzimy, że aby
spodziewamy się, że liczba ogniskowa
Aby znaleźć stałą proporcjonalności, zauważmy, że
To daje
| (2.9) |
(Zadanie 2.50).
2.2. Kryterium Poincarégo–Bendixsona
Problem badania cykli granicznych okazuje się bardzo trudny. Swiadczy o tym następujący problem nierozwiązany do dziś.
Hipoteza 2.15 (Szesnasty Problem Hilberta). 7W istocie jest to druga część 16-go Problemu Hilberta. Pierwsza
część dotyczy liczby i położenia składowych spójnych (tzw. owali) dla rzeczywistych krzywych algebraicznych postaci
| (2.10) |
Uwaga 2.16. Wiadomo, że liczba cykli granicznych dla
pojedynczego pola postaci (2.10) jest skończona (Yu. Ilyashenko i J.
Ecalle), ale nie wiadomo czy istnieje jej ograniczenie w terminach
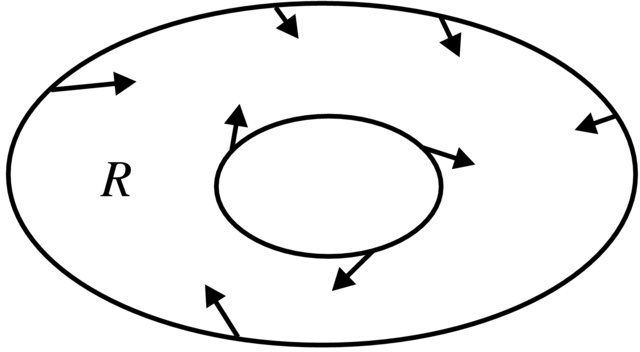
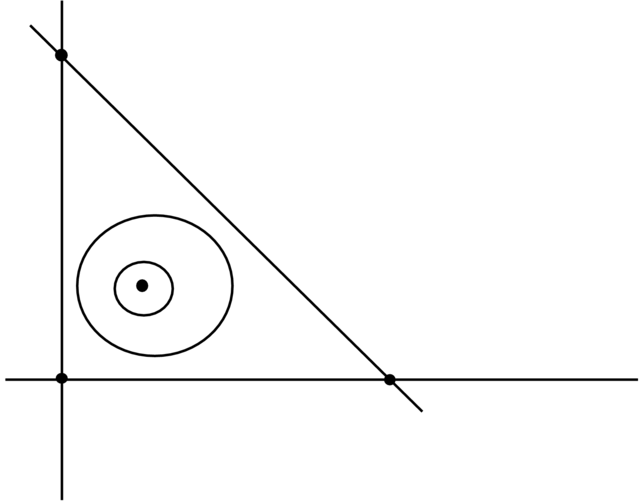
Dlatego ważne są konkretne metody pokazujące istnienie cykli granicznych lub ich brak. Prezentowane poniżej kryterium Poincarégo–Bendixsona gwarantuje nam istnienie przynajmniej jednego cyklu granicznego pod warunkiem, że pole wektorowe jest analityczne (patrz Stwierdzenie 2.10).
Załóżmy, że mamy pole wektorowe
(i) pole
(ii) pole
Twierdzenie 2.17 (Poincaré–Bendixson). Przy tych założeniach wewnątrz obszaru
W dowodzie tego twierdzenia wykorzystuje się następujące ważne pojęcie w Układach Dynamicznych.
Definicja 2.18.Zbiorem
(lub
W przypadku punktów skupienia ujemnej orbity punktu
Oczywiście przyciągający cykl graniczny jest zbiorem
Twierdzenie 2.19.Jeśli dla pola wektorowego
(a) ograniczony i
(b) nie zawiera punktów równowagi pola,
to
Dowód. Niech
W tym celu wybierzmy lokalne cięcie (odcinek)
Oczywiście
Przypuśćmy, że krzywa
Teraz deformując nieznacznie kawałek trajektorii
zauważmy, że
Dowód Twierdzenia 2.17. Bierzemy dowolny punkt
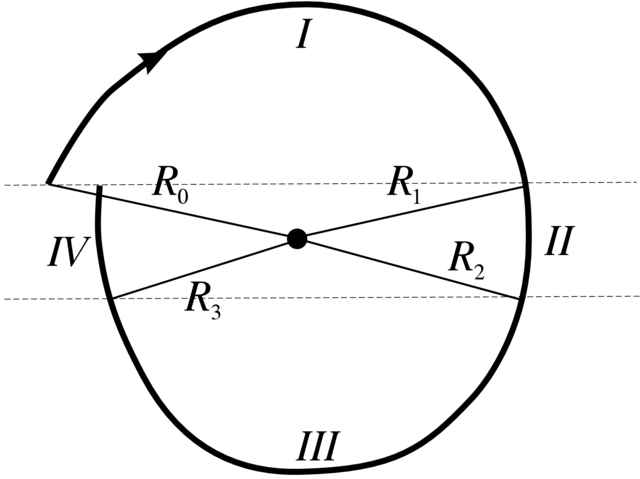
Przykład 2.20.8Ten przykład pochodzi z monografii “Modern
Geometry” Dubrovina, Novikova i Fomenko. Niestety tam nie
ma pewnych istotnych detali, które uzupełniłem. Ponadto układ Liénarda zwykle przyjmuje formy
| (2.11) |
gdzie
Zauważmy, że jedyny punkt równowagi
dla małego
Chciałoby się wybrać zewnętrzny brzeg w postaci dużego okręgu
pokazuje, że w obszarze
Aby wszystko uściślić, rozważmy cztery obszary płaszczyzny
(I, II, III, IV), w których badamy
Startujemy z punktu
gdzie
Wkraczamy do obszaru II z promieniem
i mamay oszacowanie
dla pewnej stałej
Analogicznie jak w obszarze I dostajemy
dla stałej
Zatem promień
Słuchacze mogą zapytać, dlaczego w twierdzeniu Poincarégo–Bendixsona obszar
Twierdzenie 2.21.Wewnątrz obszaru ograniczonego przez zamkniętą krzywą fazową pola wektorowego na płaszczyźnie istnieje co najmniej jeden punkt osobliwy tego pola.
Dowód tego wyniku używa metod topologicznych, a dokładniej, pojęcia indeksu.
Definicja 2.22. Niech
| (2.12) |
Indeksem
Jeśli
Przykłady 2.23. Dla pola
Stwierdzenie 2.24.Dla dodatnio zorientowanej krzywej
gdzie sumowanie biegnie po punktach osobliwych pola wewnątrz
obszaru ograniczonego przez krzywą
Dowód. Zauważmy, że odwzorowanie
jest funkcją ciągłą na przestrzeni par
Możemy zdeformować krzywą do krzywej
Lemat 2.25.Jeśli
Dowód. Korzystając z własności niezmienniczości
indeksu względem deformacji (w klasie (2.12)) możemy zdeformować
krzywą i pole tak, aby otrzymać
Następujący wniosek uściśla Twierdzenie 2.21.
Wniosek 2.26. Jeśli
gdzie sumujemy po punktach równowagi pola wewnątrz obszaru
zakreślonego przez krzywą
2.3. Kryterium Dulaca
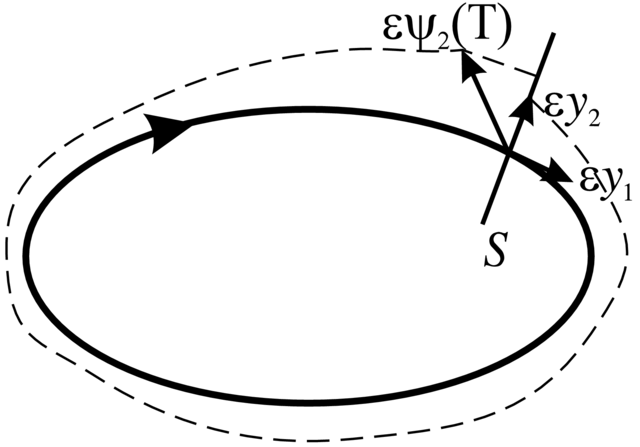
Rozważmy pole wektorowe
Definicja 2.27. Liczba
Twierdzenie 2.28 (Dulac). Mamy
gdzie
Dowód. Rozważmy równanie w wariacjach względem
warunków początkowych wzdłuż rozwiązania
(patrz wzór (6.13)). Wybierzmy dwa warunki początkowe dla tego równania:
Zgodnie ze wzorem (6.28) rozwiązania
Zauważmy teraz, że równoległobok rozpięty przez wektory
Ale Twierdzenie 6.23, czyli
Twierdzenie Dulaca okazuje się być użyteczne przy pokazywaniu braku cykli granicznych dla pewnych pól wektorowych. Zilustrujemy to na następującum przykładzie.
Przykład 2.29 (Układ Jouanolou). Ma on następującą postać
Zgodnie z Twierdzeniem 2.21 każdy cykl graniczny tego pola powinien okrążać przynajmniej jeden punkt osobliwy. Równania punktów
osobliwych, czyli
Część liniowa układu w tym punkcie zadaje się macierzą
z równaniem charakterystycznym
Przypuśćmy, że
Z drugiej strony, dywergencja pola Jouanolou wynosi
Widać, że jeśli
Jeśli
Twierdzenie Dulaca ma jeszcze inne zastosowania.
Definicja 2.30. Funkcja
Twierdzenie 2.31.Jeśli dla pola wektorowego
Dowód. Pomnożenie pola wektorowego przez funkcję dodatnią nie zmienia portretu fazowego tego pola. Zmienia się tylko prędkość punktu (tj. rozwiązania) wzdłuż krzywej fazowej. ∎
Uwaga 2.32. Można w Twierdzeniu 2.31 dopuścić nieostre
nierówności
Przykład 2.33. (Uogólniony układ Lotki–Volterry). Jest to układ opisujący zmianę populacji drapieżników i ofiar (np. wilków i zajęcy)
(z
jeśli
Aby to potwierdzić, rozważmy następującą kandydatkę na funkcję Dulaca
Sprawdzamy (z
Jeśli
Jeśli
(przy
Przykład 2.34 (Równanie van der Pola). Jest to następujący układ
szczególny przypadek układu Liénarda. Pojawia się on w
elektrotechnice, dla układu składającego się z kondensatora o
pojemności
to jest właśnie oryginalne równanie van der Pola. Po
zamianie
Udowodnimy, że:
układ van der Pola posiada dokładnie jeden cykl graniczny.
Po pierwsze zauważmy, że
Rozważmy funkcję
gdzie
a stała
Okazuje się, że funkcja
jest funkcją Dulaca dla układu van der Pola w obszarze
Rzeczywiście, mamy
gdzie
i
Stąd otrzymujemy dwa wnioski:
(a)
(b) W obszarze
Pozostaje jeszcze udowodnić, że w obszarze
Z własności (a) wynika, że na kawałkach brzegu w
wynika, że
czyli przyrost
Powyższy dowód jednoznaczności cyklu granicznego pochodzi od L.
Czerkasa z Mińska Białoruskiego. W Zadaniu 4.17 poniżej
proponujemy inny dowód jednoznaczności cyklu granicznego w
przypadku, gdy parametr
2.4. Rysowanie portretów fazowych na płaszczyźnie
Jak już było powiedziane w Definicji 2.1 portret fazowy pola
wektorowego
2.4.1. Punkty osobliwe
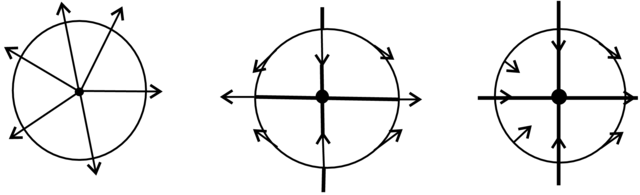
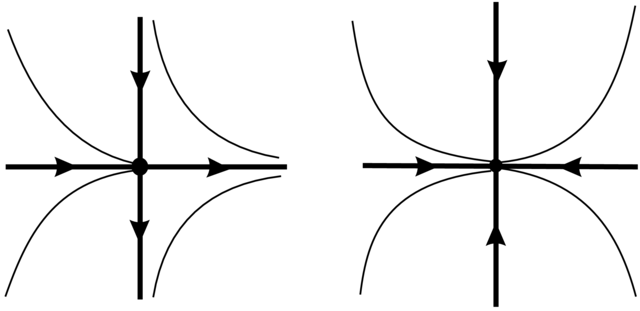
Dzielą się one na elementarne i nieelementarne.Przy tym elementarne punkty osobliwe można podzielić na niezdegenerowane i zdegenerowane.
Definicja 2.35. Punkt równowagi
Punkt równowagi
siodłem, jeśli
węzłem stabilnym (odpowiednio węzłem
niestabilnym), jeśli
ogniskiem stabilnym (odpowiednio ogniskiem
niestabilnym), jeśli
siodło–węzłem, jeśli
Lokalne portrety fazowe w otoczeniu elementarnych punktów osobliwych zdefiniowanych powyżej są przedstawione na Rysunkach 2.17 i 2.18.
Uwaga 2.36. W przypadku
Uwaga 2.37. Pojęcie siodła–węzła podane powyżej jest dosyć szerokie. Rzecz w tym, że możemy mieć następujące modelowe sytuacje
| (2.13) | |||||
| (2.14) |
W Podrozdziale 3.3 poniżej wzory (2.13)–(2.14) będą dokładniej uzasadnione. Gdy
Z punktu widzenia topologicznego lokalny portret fazowy nie zależy od
Uwaga 2.38 (Nieelementarne punkty osobliwe). Przypomnę, że
tutaj mamy
Polega ona na prostej operacji wprowadzenia biegunowych współrzędnych
| (2.15) |
to w zmiennych biegunowych dostajemy
| (2.16) |
gdzie
Zauważmy, że prawe strony równań (2.16) zerują się
przy
Ale po takiej operacji dostajemy pole wektorowe na cylindrze
W przeciwnym przypadku powtarzamy procedurę rozdmuchania (połączo-
ną z dzieleniem) w otoczeniu każdego nieelementarnego punktu
osobliwego
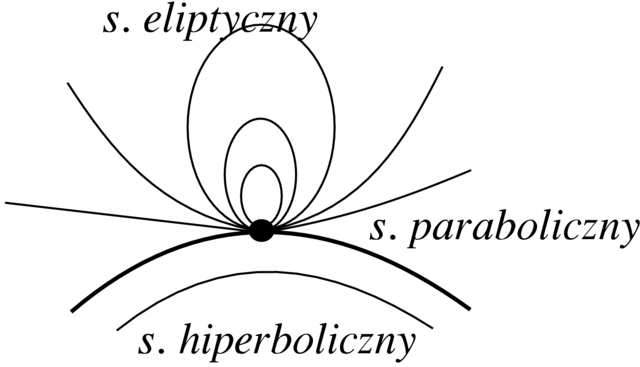
W przypadku nieelementarnego punktu osobliwego często jego otoczenie można podzielić na sektory: hiperboliczne, paraboliczne, i eliptyczne. Są one zobrazowane na Rysunku 2.19. Jest pewna teoria związana z nimi, którą nie będziemy się zajmować. Zainteresowanych słuchaczy odsyłam do książki P. Hartmana [13].
2.4.2. Zamknięte krzywe fazowe
One odpowiadają rozwiązaniom (i trajektoriom) okresowym i były dosyć szczegółowo omawiane w poprzednim podrozdziale.
2.4.3. Separatrysy punktów osobliwych
Definicja 2.39.Separatrysą punktu osobliwego
Na przykład, dla siodła separatrysami są składowe `nakłutych'
rozmaitości stabilnej
W ogólnym przypadku, gdy mamy podział na sektory hiperboliczne, eliptyczne i paraboliczne, separatrysy występują na brzegach sektorów hiperbolicznych.
Uwaga 2.40. Ważnym elementem portretu fazowego pola wektorowego
jest `los' drugiego końca danej separatrysy
Może on lądować w innym punkcie osobliwym
Drugi koniec separatrysy może też nawijać się na cykl graniczny.
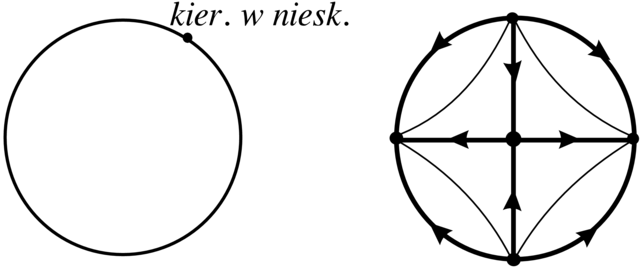
2.4.4. Zachowanie na nieskończoności
Istnieje wiele uzwarceń płaszczyzny
Uzwarcenie Poincarégo jest przydatne przy badaniu zachowania się
krzywych fazowych wielomianowych pól wektorowych, tzn. takich układów
Wtedy w otoczeniu okręgu w nieskończoności można wpropwadzić współrzędne typu biegunowego
Dostaniemy układ postaci
czyli z biegunem w zbiorze
Zauważmy, że punkty osobliwe
Przykład 2.41. Liniowe pole wektorowe
2.4.5. Orbitalna równoważność
Definicja 2.42. Dwa pola wektorowe
Pole wektorowe
Jak łatwo się przekonać, powyższa definicja orbitalnej równoważności i orbitalnej strukturalnej stabilności jest słabsza od definicji równoważności i strukturalnej stabilności podanej w Definicji 1.24.
Zatem z Twierdzenie Grobmana–Hartmana (Twierdzenie 1.23) i następującego po nim Stwierdzenia 1.25 wynika, że dwa pola wektorowe w otoczeniu hiperbolicznych punktów osobliwych o takich samych wymiarach rozmaitości stabilnej i niestabilnej są orbitalnie równoważne. Są one też orbitalnie strukturalnie stabilne.
Poniżej, bez dowodu podajemy warunki konieczne dla orbitalnej strukturalnej stabilności pola wektorowego na płaszczyźnie.
Twierdzenie 2.43.Jeśli pole
(i) jego punkty osobliwe są hiperboliczne,
(ii) jego zamknięte krzywe fazowe są hiperbolicznymi cyklami granicznymi,
(ii) nie ma połączeń separatrys.
Jeśli obszar
ZADANIA
Zadanie 2.44. Wyliczyć rozwiązanie układu
Zadanie 2.45. Analogicznie jak w przypadku wahaddła matematycznego znaleźć całkę pierwszą i naszkicować krzywe fazowe dla układu Duffinga
Wyliczyć rozwiązanie z warunkiem początkowym
Zadanie 2.46. Wyliczyć
Zadanie 2.47. Pokazać, że wartości własne macierzy
Zadanie 2.48. Udowodnić wzór (2.4).
Zadanie 2.49. Wyliczyć współczynnik
Zadanie 2.50. Przy założeniu, że po prawej stronie równania (2.7) występują tylko wyrazy kwadratowe (tj.
Zadanie 2.51. Pokazać, że dla liniowego pola wektorowego
liczba cykli granicznych wynosi
Zadanie 2.52. Pokazać, że zbiór
Zadanie 2.53. Pokazać, że w dowodzie Twierdzenia 2.19
kolejne punkty
Zadanie 2.54. Pokazać, że pole wektorowe (2.11) ma własność, że kwadrat promienia
Zadanie 2.55. Policzyć indeks w
Zadanie 2.56. Pokazać, że
Zadanie 2.57. Pokazać, że pole wektorowe
Zadanie 2.58. Pokazać, że wykładnik charakterystyczny orbity okresowej zdefiniowany w Definicji 2.27 jest dobrze określony.
Zadanie 2.59. Uzupełnić analizę układu Jouanolou w
przypadku nieparzystego
Zadanie 2.60. Wyliczyć div
Zadanie 2.61. Naszkicować portret fazowy (w
Zadanie 2.62. Naszkicować portret fazowy dla układu
Zadanie 2.63. Naszkicować portret fazowy dla równań
Zadanie 2.64. Rozważmy pole wektorowe
(a) Zacznijmy od prostszego pola wektorowego
| (2.17) |
Robiąc podstawienie
(b) Stosując dwukrotnie rozdmuchanie pokazać, że pola
(c) Pokazać, że dodanie składnika
(d) Pokazać, że również pozostałe punkty z
otoczenia