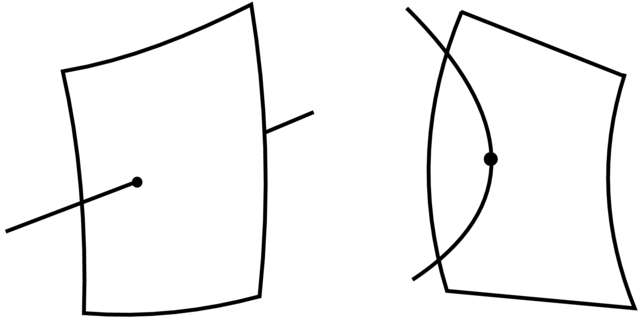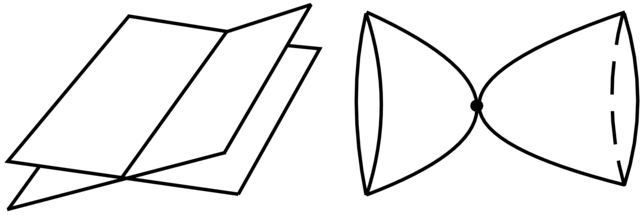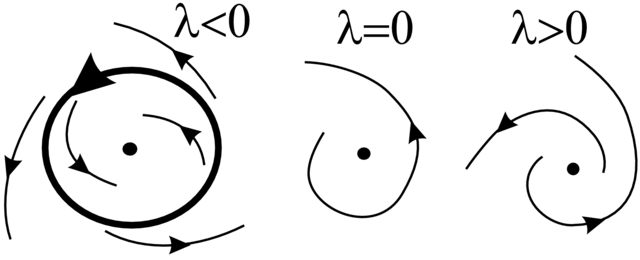Zagadnienia

3.1 Wersalność
3.2 Transwersalność
3.3 Bifurkacje kowymiaru 1

3. Teoria bifurkacji

3.1. Wersalność

Zgodnie z Twierdzeniem 2.43 typowe pola wektorowe na zwartej 2-wymia- rowej rozmaitości M są orbitalnie strukturalnie stabilne. Jeśli oznaczymy przez X nieskończenie wymiarową przestrzeń wszystkich pól wektorowych na M (danej klasy i z odpowiednią topologią, o której nie będziemy mówić), to podzbiór Σ, nazywany zbiorem bifurkacyjnym, przestrzeni Xzłożony z pól, które nie są orbtalnie strukturalnie stabilne, powinien mieć kowymiar ≥1. Należy się spodziewać, że ten podzbiór Σ jest na ogół gładki, ale może mieć punkty nieregularne (jak na Rysunku 3.1). Te ostatnie punkty powinny odpowiadać polom wektorowym, które mają osobliwości bardziej skomplikowane niż pola odpowiadające typowym punktom z Σ.

Rys. 3.1. Zbiór bifurkacyjny.

Jeśli wybierzemy przypadkowo pojedyncze pole z X, to z prawdopodobieństwem 1 będzie ono poza zbiorem Σ. Ale cała rodzina vλλ∈R pól wektorowych stanowi krzywą w X i już może przeciąć hiperpowierzchnię Σ. Spodziewamy się też, że dla typowej rodziny odpowiednia krzywa przetnie hiperpowierzchnię Σ pod kątem i w punktach typowych tej hiperpowierzchnii (patrz Rysunek 3.1).

Teoria bifurkacji zajmuje się badaniem zarówno geometrii zbioru bifurkacyjnego Σ jak i zachownia się wieloparametrowych rodzin pól wektorowych. My ograniczymy się do 1-parametrowych rodzin.

Należy zwrócić uwagę na jeszcze jeden aspekt tej sytuacji. Na przestrzeni X działa grupa G orbitalnych równoważności i podzbiór bifurkacyjny Σ jest niezmienniczy względem tego działania. Należy zatem powiązać analizę 1-parametrowych rodzin vλ z działaniem grupy G. V. Arnold w [5] wprowadził raz na zawsze porządek na tym polu i poniższe definicje pochodzą od niego. My podajemy te definicje dla 1-parametrowych rodzin, ale łatwo je uogólnić na przypadek wieloparametrowy.¹¹Ta filozofia pracuje również w innych ogólnych sytuacjach. Na przykład, gdy X jest przestrzenią funkcji f na rozmaitości a G jest grupą dyfeomorfizmów h rozmaitości z działaniem f⟼f∘h. Podobnie X może być przestrzenią dyfeomorfizmów f rozmaitości M a grupa G dyfeomorfizmów M może działać poprzez sprzężenie: f⟼h∘f∘h-1.

Definicja 3.1. Dwie rodziny vλλ∈J i wλλ∈J, J⊂R, pól wektorowych na M są orbitalnie równoważne, jeśli dla każdego λ∈J pola vλ⁢x i wλ⁢x są orbitalnie równoważne za pomocą homeomorfizmu hλ⁢x, który zależy w sposób ciągły od parametru λ.

Mówimy, że rodzina wνν∈K jest indukowana z rodziny vλλ∈J, jeśli istnieje ciągłe od wzorowanie φ:K⟼J takie, że

wν=vφ⁢ν.

Rodzina vλλ∈R,0, z zadanym polem v0, jest wersalna, jeśli dowolna inna rodzina wνν∈R,0 z w0=v0 jest orbitalnie równoważna rodzinie indukowanej z rodziny vλ.

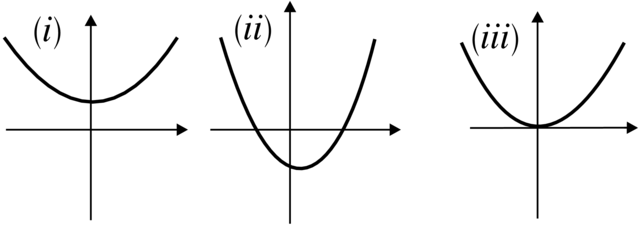
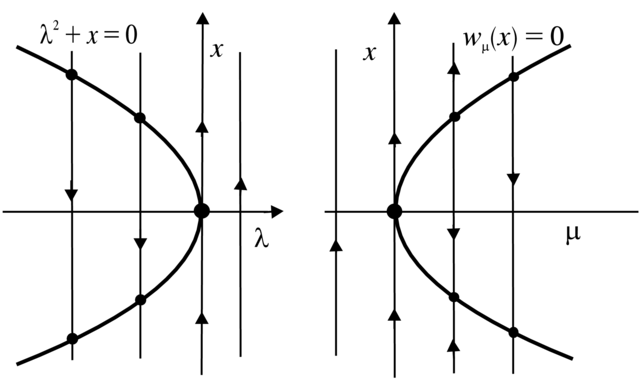
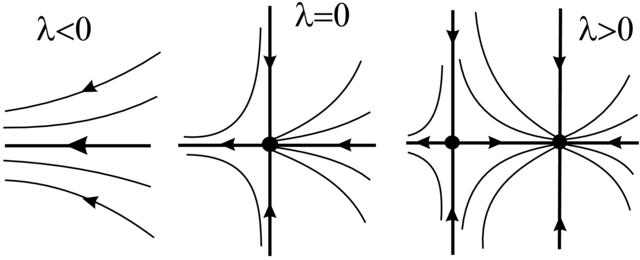
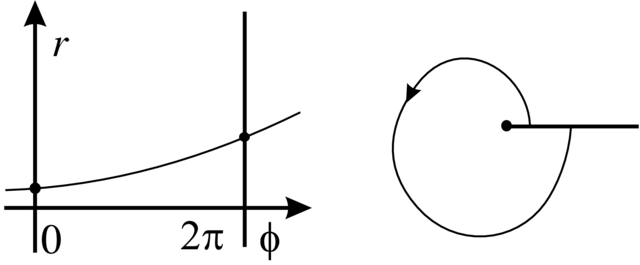
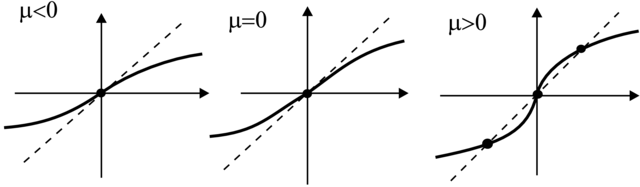
Przykład 3.2. Rodzina x˙=ν2+x3 jest indukowana z rodziny x˙=λ+x3 przy pomocy zamiany zmiennych λ=φ⁢ν=ν2.

Przykład 3.3. Weźmy modelową rodzinę pól wektorowych

x˙=vλ⁢x=λ+x2.

(3.1)

Odpowiednie portrety fazowe są przedstawione na Rysunku 3.2.

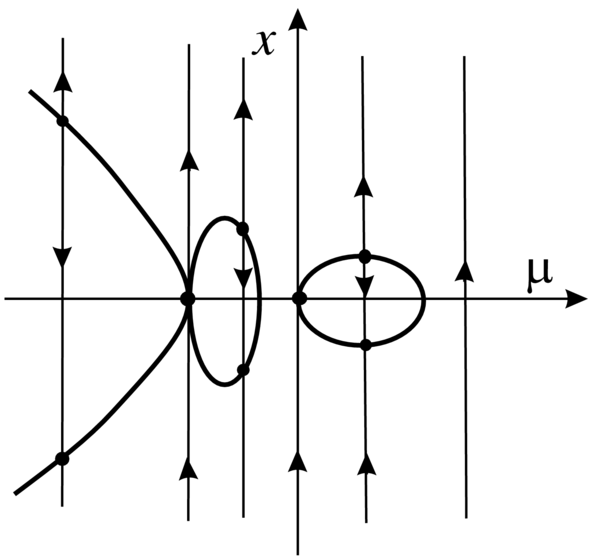
Weźmy teraz dowolną rodzinę postaci

x˙=wμ(x)=x2+μw~(x,μ)=:f(x,μ),

(3.2)

gdzie w~⁢x,μ jest gładką funkcją w otoczeniu x=μ=0. Twierdzę, że

Rys. 3.2. Portrety fazowe.

dla dażdego μ pole wektorowe wμ posiada albo 1 albo 2 albo 0 punktów osobliwych w otoczeniux=0. Aby to zobaczyć rozważmy równanie

g⁢x,μ=0,

gdzie g⁢x,μ=fx′⁢x,μ. Ponieważ fx⁢x′′⁢0,0≠0, to gx′⁢0,0≠0, i z Twierdzenia o Funkcji Uwikłanej wynika istnienie gładkiej funkcji ψ⁢μ takiej, że jest spełnione równanie g⁢ψ⁢μ,μ≡0. To oznacza, że punkt

xμ=ψ⁢μ

Rys. 3.3. Wykresy prawej strony.

jest punktem lokalnego minimum funkcji wμ=f(⋅,μ): d⁢wμd⁢x⁢xμ=0. Mamy trzy możliwości na wartość pola wμ w punkcie xμ: (i) wμ⁢xμ=0, (ii) wμ⁢xμ<0, (iii) wμ⁢xμ>0. W przypadku (i) pole wμ ma dokłanie jeden punkt równowagi (typu siodło–węzeł), w przypadku (ii) pole wμ ma dwa hiperboliczne punkty równowagi a w przypadku (iii) nie ma żadnych punktów równowagi (patrz Rysunek 3.3).

Zatem dla każdego μ portret fazowy pola wμ jest topologicznie równoważny z portretem fazowym pola vλ dla odpowiedniego λ. Pojawia się naturalne pytanie, czy można tak dobrać λ=φ⁢μ i homeomorfizmy hμ realizujące orbitalne sprzężenie wμ z vφ⁢μ, aby zależność od μ była ciągła. Okazuje się, że tak; to oznacza, że rodzina (3.1) jest wersalna.

Rys. 3.4. Bifurkacja modelowej rodziny i bifurkacja typowej rodziny.

Aby się o tym przekonać, rozważmy najpierw przypadek, gdy

(a)∂⁡f∂⁡μ⁢0,0≠0 w (3.2). Wtedy krzywa punktów równowagi

Γ:wμ⁢x=f⁢x,μ=0

pola wμ na płaszczyżnie zmiennych x,μ jest `pionowa' i homeomorficzna z parabolą (patrz Rysunek 3.4). Również parabolą jest krzywa punktów równowagi Δ={λ=-x2} dla pola vλ.

W zależności od znaku fμ′⁢0,0 kładziemy φ⁢μ=μ lub φ⁢μ=-μ; czyli dalej można zakładać, że obie `parabole' są zorientowane tak samo. W tym przypadku konstrukcję homeomorfizmów hμ, czyli homeomorfizmu płaszczyzny

μ,x⟼μ,hμ⁢x,

rozpoczynamy od konstrukcji homeomorfizmu pomiędzy krzywymi punktów równowagi: Γ⟼Δ. Następnie przedłużamy ten homeomorfizm do homeomorfizmu płaszczyzny, tak aby odcinki pionowe (w μ=const) poza punktami równowagi przechodziły na odpowiednie odcinki pionowe. Jest raczej jasne, że tak da się zrobić.

(b) W zdegenerowanym przypadku, gdy fμ′⁢0,0≠0, krzywa punktów równowagi Γ={f=0} może być bardzo skomplikowana (patrz Rysunek 3.5). Ale wiemy, że z każdą prostą pionową μ=const ta krzywa ma co najwyżej dwa punkty przecięcia. Oznaczmy Γμ przecięcie Γ z taką prostą. Zatem konstrukcja przeparametryzowania μ⟼φ⁢μ polega na tym aby parametry μ, dla których #⁢Γμ=2, przeszły na lewo od λ=0 a parametry μ, dla których #⁢Γμ=0 przeszły na prawo od λ=0 (z zachowaniem ciągłości). Następnie, powtarzając argumenty z przypadku (a), konstrujemy najpierw ciągłe przekształcenie μ,x⟼φ⁢μ,hμ⁢x pomiędzy krzywymi Γ i Δ a następnie przedłużamy je w sposób ciągły z zachowaniem pionowości.

Rys. 3.5. Bifurkacja nietypowej rodziny.

3.2. Transwersalność

Matematycznym aparatem do ścisłego sformułowania teorii bifurkacji i odpowiednich twierdzeń jest teoria transwersalności sformułowana przez francuskiego matematyka R. Thoma.

Niech M będzie n-wymiarową rozmaitością a B⊂M będzie jej k-wymiarową podrozmaitością. Ponadto niech A będzie m-wymarową rozmaitością a

f:A⟼M

będzie odwzorowaniem różniczkowalnym (o wystarczającej klasie różniczkowalności). W przypadku zwartych rozmaitości A i M w przestrzeni Ck⁢A,M odwzorowań wprowadza się naturalną topologię (której nie będę uściślał).

Definicja 3.4. Mówimy, że odwzorowanie f jest transwersalne do podrozmaitości B, jeśli dla każdego punktu x∈A takiego, że y=f⁢x∈B, ma miejsce następująca własność

f∗⁢Tx⁢A+Ty⁢B=Ty⁢M.

Gdy A⊂M jest podrozmaitością i f=i⁢dA jest włożeniem, to mówimy, że A jest transwersalne do B, gdy własność

Ty⁢A+Ty⁢B=Ty⁢M

zachodzi dla każdego punktu y∈A∩B. Mamy standardowe oznaczenia

Rys. 3.6. Transwersalność krzywych na płaszczyźnie.

f⋔B⁢ i ⁢A⋔B

dla własności transwersalności.

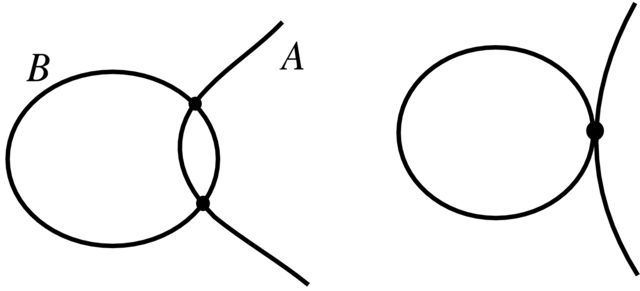
Przykład 3.5. (a) Niech M=R2 oraz A⊂M i B⊂M będą gładkimi krzywymi. Wtedy A⋔B gdy krzywa A przecina krzywę B pod niezerowym kątem (patrz Rysunek 3.6).

(b) Niech M=R3, A⊂M to krzywa i B⊂M to powierzchnia. Rysunek 3.7 pokazuje przypadki transwersalności i nietransweralsności.

(d) Gdy M=R3 i A⊂M, B⊂M są krzywymi, to A⋔B wtedy i tylko wtedy gdy krzywe są rozłączne.

(e) Niech M=R2=x,y, A=R1 i B={x=0} oraz niech f:A⟼M będzie zadane wzorem f⁢t=t3,0. Oczywiście f⁢t∈B tylko dla t=0. Ale wtedy f∗⁢0=f′⁢0=0. Zatem f∗⁢T0⁢A+T00⁢B=T0,0⁢B≃B≠T0,0⁢M. Ten przykład pokazuje zasadność własności transwersalności odwzorowania to podrozmaitości.

Zachodzi następujące fundamentalne twierdzenie pochodzące od Thoma¹²To Twierdzenie Thoma o Transwersalności, jak również jego uogólnienie podane poniżej, stanowiły istotny element stworzonej przez niego Teorii Katastrof . Ta teoria zawiera w sobie po części teorię osobliwości odwzorowań i funkcji jak również teorię bifurkacji układów dynamicznych. Warto jeszcze dodać, że w przypadku uogólnienia Twierdzenia Thoma na przypadek rozmaitości niezwartych wprowadza się specjalną topologię (tzw. topologię Whitney'a) w przestrzeni odwzorowań klasy Ck..

Twierdzenie 3.6 (Thom). Niech M, A i B będą ustalonymi zwartymi rozmaitościami jak powyżej. Wtedy podzbiór przestrzeni odwzorowań f:A⟼M złożony z odwzorowań, które są transwersalne do B, jest otwarty i gęsty.

To oznacza, że, z jednej strony, jeśli odwzorowanie f0 jest transwersalne do B, to dowolne bliskie niemu odwzorowanie fε też jest transwersalne do B, a, z drugiej strony, jeśli f0 nie jest transwersalne, to dowolnie blisko niego istnieje odwzorowanie fε, które już jest transwersalne.

Rys. 3.7. Transwersalność krzywej i powierzchni w przestrzeni.

Dowód. Nietrudno zauważyć, że można ograniczyć się do sytuacji lokalnej, gdy A⊂Rm i M⊂Rn są podzbiorami otwartymi a

B={y1=…=yn-k=0}∩M

jest (lokalnie) podprzestrzenią kowymiaru n-k (Zadanie 3.16).

Wtedy f⁢x=f1⁢x,…⁢fn⁢x i

Ty⁢B=q∈Rn:q1=…=qn-k=0⊂Ty⁢M=Rn.

Jeśli f⁢x0∈B, tzn. f1⁢x0=…⁢fn-k⁢x0=0, to f jest transwersalne w x0 do B wtedy i tylko wtedy gdy wektory f∗⁢∂x1,…,f∗⁢∂xm razem z wektorami ∂y⁢n-k+1,…⁢∂yn rozpinają Rn. (Tutaj ∂xj i ∂yk są bazowymi wektorami w Rm i Rn odpowiednio.) Do tego wystarczy, aby rzuty wektorów f∗⁢∂xj na przestrzeń ilorazową Ty⁢M/Ty⁢B≃Rn-k rozpinały tę przestrzeń. To oznacza, że macierz

C=∂⁡f1/∂⁡x1…∂⁡f1/∂⁡xm………∂⁡fn-k/∂⁡x1…∂⁡fn-k/∂⁡xm

ma rząd rk⁢C≥n-k.

Mamy dwie możliwości:

(i) m<n-k i wtedy rząd jest mniejszy od n-k,

(ii) m≥n-k (wtedy własność rkC≥n-k jest warunkiem otwartym w przestrzeni macierzy). W przypadku (i) transwersalność oznacza brak przecięcia f⁢A z B i jest to warunek otwarty w przestrzeni odwzorowań. Również w przypadku (ii) nietrudno pokazać, że warunek transwersalności też jest otwarty (Zadanie 3.13).

Aby udowodnić gęstość własności transwersalności musimy wprowadzić dodatkowe pojęcia (Zadanie 3.14).

W przypadku (ii) weźmy lokalne odwzorowanie g:A⟼Rn-k,

g⁢x=f1⁢x,…,fn-k⁢x.

Przypomnijmy (patrz Definicja 3.7 poniżej), że x0 jest punktem krytycznym dla g, jeśli rk∂⁡g∂⁡x⁢x0 =rkC<n-k, a wartość g⁢x0 nazywa się wartością krytyczną dla g. Skorzystamy z klasycznego Twierdzenia Sarda (Twierdzenie 3.7 poniżej), które zapewnia, że zbiór wartości krytycznych dla g jest `rzadki'. Zgodnie z Zadaniem 3.15 f⋔B, gdy 0 nie jest wartością krytyczną dla g. Niech z będzie wartością niekrytyczną dla g i bliską zeru. Zaburzymy odwzorowanie f=g,h w następujący sposób

fε⁢x=g⁢x-z,h⁢x.

Latwo sprawdzić, że fε jest transwersalne do B (Zadanie 3.16). ∎

Rys. 3.8. Transwersalność powierzchnii w przestrzeni.

Definicja 3.7. Niech h:Rm⟼Rl będzie odwzorowaniem różniczkowalnym. Mówimy, że że x0 jest punktem krytycznym dla h jeśli rk∂⁡h∂⁡x⁢x0 nie jest maksymalny. Wartość h⁢x0 w punkcie krytycznym nazywa się wartością krytyczną dla h.

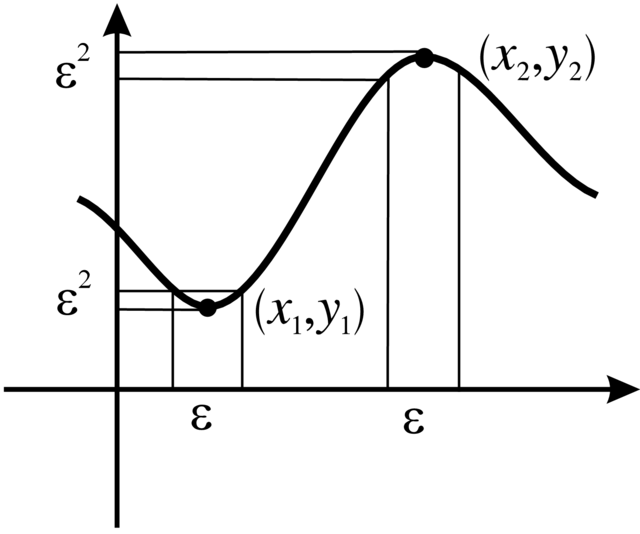
Twierdzenie 3.8 (Sard). Zbiór wartości krytycznych dla odwzorowania różniczkowalnego h:Rm⟼Rl dostatecznie wysokiej klasy gładkości ma zerową miarę Lebesque'a.

Uzasadnienie. Rozważmy przypadek m=l=1. Nie jest wykluczone, że wartości krytyczne dla g mogą tworzyć zbiór gęsty w R.

Możemy jednak pokryć każdy punkt krytyczny xj odcinkiem Ij o szerokości Ij≤ε dla dowolnie małego ε. Ponieważ g′⁢xj=0, to długość obrazu g⁢Ij takiego odcinka będzie szerokości rzędu O⁢ε2=O⁢ε⁢Ij (patrz Rysunek 3.9). Zatem

g⁢⋃Ij≤O⁢ε⋅⋃Ij≤O⁢ε,

co dąży do zera przy ε→0.

W istocie ten sam argument pracuje przy dowolnych m≤l (Zadanie 3.17). Gdy m>l dowód jest bardziej skomplikowany (z rozbiciem Rm na podzbiory stałego rzędu macierzy ∂h/∂x). ∎

Rys. 3.9. Twierdzenie Sarda.

Następująca definicja jest potrzebna do uogólnienia Twierdzenia Thoma. Niech

f:Rm⟼Rn

(3.3)

będzie odwzorowaniem dostatecznie wiele razy różniczkowalnym. Z takim odwzorowaniem można związać serię geometrycznych obiektów. Pierwszym z nich jest wykres

{(x,f(x))}⊂Rm×Rn=:J0(Rm,Rm).

Innym jest wykres pochodnej, czyli wykres odwzorowania D⁢f:x⟼y,p=f⁢x,∂⁡f∂⁡x⁢x,

{(x,f(x),∂⁡f∂⁡x(x))}⊂Rm×Rn×Rm⋅n=:J1(Rm,Rn).

Ogólnie, wykres odwzorowania r-tej pochodnej odwzorowaniax⟼f⁢x,D⁢f⁢x,…,Dr⁢f⁢x jest podzbiorem (dosyć dużej) przestrzeni oznaczanej przez Jr⁢Rm,Rn.

Definicja 3.9. Przestrzenie Jr⁢Rm,⁢Rn nazywają się przestrzeniami dżetów rzędu r odzworowań z Rm do Rn. Z każdym odzworowaniem postaci (3.3) wiąże się jego r-ty dżet

x⟼jr⁢f⁢x=x,f⁢x,D⁢f⁢x,…,Dr⁢f⁢x∈Jr⁢Rm,Rn.

Analogicznie, jeśli A i M są rozmaitościami wymiarów m i n odpowiednio, to definiuje się przestrzenie Jr⁢A,M dżetów odwzorowań z A do M i z każdym różniczkowalnym odwzorowaniem f:A⟼M wiąże się jego rty dżet jr⁢f:A⟼Jr⁢A,M.

Definicja 3.10. Jeśli C⊂Jr⁢A,M jest podrozmaitością, to mówimy, że odwzorowanie f:A⟼M jest transwersalne do C (oznaczenie f⋔C) gdy jr⁢f⋔C.

Twierdzenie 3.11 (Thom). Niech A, M i C⊂Jr⁢A,M będą ustalone. Wtedy zbiór odwzorowań f:A⟼M, które są transwersalne do C, jest otwarty i gęsty w zbiorze wszystkich takich odwzorowań.

Dowód. Ten dowód w znacznej części powtarza dowód Twierdzenia 3.6. Podstawowa różnica leży w dowodzie gęstości, a dokładniej, w wyborze zaburzenia. Otóż, zamiast zamiany g⁢x→g⁢x-z (gdzie z jest `małą' wartością niekrytyczną dla g), bierze się zamianę g⁢x→g⁢x-z-p~⁢x-q~⁢x,x-…-s~⁢x,…⁢x, gdzie p~, q~, …,s~ są odpowiednio `małymi' przekształeceniami liniowymi, jednorodnymi kwadratowymi, czy jednorodnymi stopnia r. ∎

Przykład 3.12. Pewne naturalne warunki na odwzorowanie są interpretowane jako warunki na jego transwersalność w dżetach. Na przykład, warunek

∂⁡f∂⁡λ⁢x,λ⋅∂2∂⁡x2⁢f⁢x,λ≠0⁢ gdy ⁢f⁢x,λ=∂⁡f∂⁡x⁢x,λ=0

wynika z jednoczesnej transwersalności odwzorowania

j1⁢f:R2=x,λ⟼J1⁢R2,R=x,λ,y,px,pλ

do dwóch podrozmaitości

C1={y=0} i C2={y=px=0}.

Istotnie, transwersalność do C1 oznacza, że ∂⁡y∂⁡x=∂⁡f∂⁡x≠0 lub ∂⁡y∂⁡λ=∂⁡f∂⁡λ≠0 gdy y=f⁢x,λ=0. Tymczasem transweralność do C2 oznacza, że fx′fλ′fx⁢x′′fx⁢λ′′≠0 gdy y=f=0 i px=fx′=0.

W zagadnieniach teorii bifurkacji zawsze, gdy pojawiają się warunki podobnego charakteru jak w Przykładzie 3.12, możemy założyć, że albo są spełnione z prawdopodobieństwem 1 albo z takim samym przwdopodobieństwem nie mogą być spełnione. Ten drugi przypadek zachodzi gdy dim⁡A+dim⁡C<dim⁡Jr⁢A,M. Taki jest praktyczny wniosek z twierdzeń Thoma.

ZADANIA

Zadanie 3.13. W przypadku m≥n-k zauważyć, że (w dowodzie Twierdzenia 3.6) rkC≥n-k oznacza rkC=n-k. Skorzystać z Twierdzenia o Funkcji Uwikłanej aby pokazać, że f-1⁢B⊂A w otoczeniu x0 jest podrozmaitością w A kowymiaru n-k. Pokazać następnie, że dla dowolnego fε bliskiego f również fε-1⁢B jest lokalnie podrozmaitością kowymiaru n-k bliską f-1⁢B. Wywnioskować stąd i z otwartości podzbioru macierzy rzędu n-k w przestrzeni macierzy wymiaru n-k×n, że fε jest transwersalne do B w otoczeniu x0.

Zadanie 3.14. Pokazać lokalną gęstość własności transwersalności w przypadku m<n-k.

Wskazówka: Wybrać odpowiednie zaburzenie fε dla f, które nie jest transwersalne do B.

Zadanie 3.15. Pokazać, że f⋔B wtedy i tylko wtedy gdy 0 nie jest wartością krytyczną dla odwzorowania g.

Zadanie 3.16. Uzupełnić dowód Twierdzenia 3.6.

Wskazówka: Użyć odpowiedniego rozkładu jedności 1=∑φj⁢x w A związanego z lokalnymi afinicznymi mapami w A, M i B. Lokalne zaburzenia wybierać w postaci fε=g-ψk⁢x⁢zk,h⁢x, z odpowiednimi funkcjami ψk⁢x o zwartym nośniku i `małymi' wektorami zk. Na koniec skorzystać ze zwartości A.

Zadanie 3.17. Udowodnić Twierdzenie Sarda w przypadkach m<l i m=l>1.

3.3. Bifurkacje kowymiaru 1

Bifurkacje autonomicznych pól wektorowych będziemy dzielić na lokalne i nielokalne.

Lokalne bifurkacje zachodzą w otoczeniu punktu osobliwego x=0 dla wartości bifurkacyjnej parametru. Dokładniej, mamy rodzinę

x˙=v⁢x;μ

taką, że

v⁢x,0=A⁢x+….

W przypadku typowych 1-parametrowych rodzin naruszenie warunku hi- perboliczności (tzn. Re⁢λj⁢A≠0 dla wszystkich wartości własnych) zachodzi w dwu przypadkach:

1. λ1⁢A=0 i Re⁢λj⁢A≠0 dla j>1; jest to bifurkacja siodło–węzeł.

2. λ1=λ¯2=i⁢ω∈i⁢R∖0 i Re⁢λj≠0 dla j>2; jest to bifurkacja narodzin cyklu granicznego albo bifurkacja Andronowa–Hopfa.

Mamy trzy nielokalne bifurkacje związane z orbitą okresową γ dla pola v⁢x,0. Niech λj będą wartościami własnymi części liniowej przekształcenia powrotu Poincarégo. Przypomnijmy, że warunek hiperboliczności dla γ oznacza, że λj≠1 dla wszystkich j. Zatem typowe bifurkacje kowymiaru 1 mają miejsce w następujących przypadkach:

3. λ1=1 i λj≠1 dla j>1; jest to bifurkacja siodło–węzeł dla orbity okresowej.

4. λ1=-1 i λj≠1 dla j>1; jest to bifurkacja podwojenia okresu.

5. λ1=λ¯2∈S1∖1,-1. Tutaj przypadki, gdy λ1=e2⁢π⁢i⁢k/m jest pierwiastkiem z 1 stopnia m, nazywają się rezonansowymi; dodatkowo, gdy m=3,4 to mówimy o silnym rezonansie.

Rys. 3.10. Połączenie separatrys i pętla separatrys.

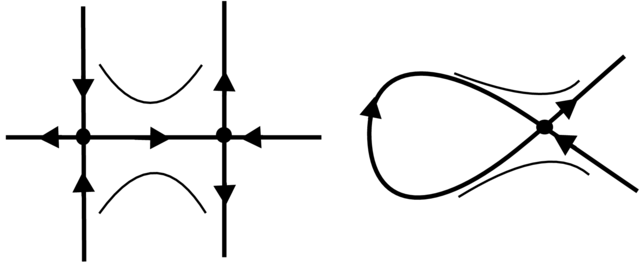
Na koniec mamy dwie nielokalne bifurkacje związane z połaczeniem separatrys (patrz Rysunek 3.10):

6. Połączenie separatrys różnych siodeł.

7. Pętla separatrys jednego siodła.

3.3.1. Redukcja do rozmaitości centralnej i forma normalna Poincarégo–Dulaca

Załóżmy, że mamy pole wektorowe

x˙=v⁢x=A⁢x+…

z punktem osobliwym x=0. Możemy założyć, że macierz A ma postać blokowo diagonalną

A=As⊕Au⊕Ac,

(3.4)

gdzie As (odpowiednio Au i Ac) ma wartości własne z Re⁢λj<0 (odpowiednio z Re⁢λj>0 i z Reλj=0).

Twierdzenie 3.18 (Szoszitaiszwili). W sytuacji jak powyżej istnieje lokalny homeomorfizm h:Rn,0⟼Rn,0 przeprowadzający portret fazowy pola v⁢x na portret fazowy następującego pola

y˙1=-y1, ⁢y˙2=y2, ⁢y˙3=w⁢y3,

(3.5)

gdzie

w⁢y3=Ac⁢y3+…

Dowód tego twierdzenia jest techniczny i skomplikowany (patrz [5]). Dlatego nie będziemy go tutaj przytaczać. Za to wyciągniemy z niego bardzo praktyczne zastosowania. Zauważmy też, że to twierdzenie jest uogólnieniem Twierdzenia Grobmana–Hartmana.

Definicja 3.19. Podrozmaitość zadaną równaniem

Wc={y1=0, y2=0}

(w terminach (3.5)) nazywamy rozmaitością centralną.

Twierszenie Szoszitaiszwiliego mówi, że w przypadku niehiperbolicznego puktu osobliwego `ciekawa część' dynamiki odbywa się na rozmaitości centralnej.

Dla rodziny pól wektorowych v⁢x,μ możemy potraktować μ jako dodatkową zmienną, tzn. mamy układ

x˙=v⁢x,μ, ⁢μ˙=0,

do którego stosujemy Twierdzenie 3.18 (z h(x,μ)=(h0(x,μ),μ)). Mamy następującą redukcję do rozmaitości centralnej.

Stwierdzenie 3.20. Dla rodziny x˙=v⁢x,μ z v⁢x,0=A⁢x+… A=As⊕Au⊕Ac, istnieje lokalny homeomeorfizm h0⁢x,μ,μ zadajający topologiczną równoważność tej rodziny z następującą rodziną

z˙=w⁢z,μ, ⁢z˙1=-z1, ⁢z˙2=z2.

Samo istnienie rozmaitości centralnej Wc jest uogólnieniem Twierdzenia Hadamarda–Perrona. Można jej poszukiwać jak w dwodzie Twierdzenia 1.19. Przy tym okaże się, że rozmaitość centralna nie jest wyznaczona jednoznacznie; zależy ona od wyboru przedłużenia pola (lub dyfeomorfizmu) na całe Rn.

Ale istnieje sposób wyznaczenia Wc w sposób formalny. Poszukujemy jej jako wykresu

Wc=x1=f⁢x3, ⁢x2=g⁢x3:x3∈Ec

(gdzie współrzędne x1,x2,x3 są związane z rozkładem (3.4)), który jest niezmienniczy względem pola v⁢x. Okazuje się, że odwzorowania f:Ec⟼Es i g:Ec⟼Eu mają jednoznacznie wyznaczone szeregi Taylora, f⁢x3,g⁢x3=O⁢x32. Na Wc, które jest parametryozwane przez x3∈Ec, otrzymujemy pole wektorowe

x˙3=w⁢x3.

Ta redukcja do Wc nazywa się redukcją Lapunowa–Schmidta.

Niestety, na ogół okazuje się, że szeregi zadające f i g są rozbieżne (nawet gdy v⁢x było analityczne). Tym też tłumaczy się niejednoznaczność Wc w sensie topologicznym.

Przykład 3.21. Rozważmy układ

x˙=x2, ⁢y˙=y-x2.

Tutaj Wu={x=0} jest rozmaitością niestabilną. Rozmaitość centralną poszukujemy w postaci Wc={y=a2x2+a3x3+…}. Podstawiając takie y do układu, dostajemy

a2⁢x2+a3⁢x3+…-x2=2⁢a2⁢x+3⁢a3⁢x2+…⋅x2.

To prowadzi do następującej rekurencji: a2=1, an+1=n⁢an, z rozwiązaniem an=n-1!. Zatem rozmaitość centralna zadaje się jednoznacznym, ale rozbieżnym, szeregiem

y=∑n≥2n-1!⁢xn

(Zadania 3.27 i 3.28).

Innym narzędziem użytecznym w teorii bifurkacji, które również opiera się na (często rozbieżnych) szeregach formalnych, jest następne twierdzenie. Rozważamy kiełki analitycznych pól wektorowych

x˙=A⁢x+O⁢x2, ⁢x∈Cn,0,

(3.6)

takich, że macierz A jest diagonalna, A=diagλ1,…,λn. Przypomnijmy jeszcze standardowe oznaczenia e1,…,en dla standardowej basy w Cn (zatem x=∑xj⁢ej), xk=x1k1⁢…⁢xnkn i k=k1+…⁢kn.

Definicja 3.22. Mówimy, że wartości własne spełniają relację rezonansową typu j,k, j∈1,…,n, k=k1,…,kn∈Nn, jeśli

λj=k1⁢λ1+…⁢kn⁢λn=k,λ.

Twierdzenie 3.23 (Poincaré–Dulac). Załóżmy że mamy kiełek zespolonego analitycznego pola wektorowego (3.6). Wtedy istnieje zamiana

x=y+O⁢y2

taka, że każda składowa po prawej stronie jest formalnym szeregiem potęgowym od y, która prowadzi do układu

y˙j=λj⁢yj+∑cj;k⁢yk, ⁢j=1,…,n,

(3.7)

przy czym sumy po prawych stronach równań (3.7) biegną po takich wielowskaźnikach k=k1,…,kn, że jest spełniona relacja rezonansowa typu j,k.

Dowód. Sprowadzanie do postaci normalnej Poincarégo–Dulaca (3.7) odbywa się przy pomocy serii zamian postaci

x=y-∑j,k:k=mbj,k⁢yk⁢ej,

(3.8)

czyli dodajemy wyrazy jednorodne stopnia m. (Zaczynamy od m=2, potem bierzemy m=3, itd.) Łatwo sprawdzić, że przekształcenie odwrotne do (3.8) ma postać y=x+∑j,k:k=mbj,k⁢yk⁢ej+… (Zadanie 3.29).

Załóżmy, że w polu (3.6) do stopnia m-1 występują tylko wyrazy rezonansowe (założenie indukcyjne). Chcemy przy pomocy podstawienia (3.8) zlikwidować wyrazy nierezonansowe stopnia dokładnie m. Mamy

x˙i=y˙i-∑k:k=mbi,k⁢yk⋅,

(3.9)

gdzie

y˙i=λiyi+(wyrazy rezon. st. ≤m)+h.o.t.

∑k:k=mbi,k⁢yk⋅=∑bi,k⋅λ,k⁢yk+h.o.t.

Z lewej strony wzoru (3.9), po podstawieniu (3.8), mamy

	x˙i	=	λi⁢yi-∑k:k=mbi,k⁢yk+wyrazy rezon. st. ≤m-1
			+∑k:k=mai,k⁢yk+h.o.t.

Teraz, porównując wyrazy jednorodne stopnia m, dostajemy równania

bi,k⋅λ,k-λi=ai,k.

Z nich jasno wynika, że jeśli λ,k-λi≠0, to można dobrać bi,k tak, aby zlikwidować odpowiedni nierezonansowy wyraz xk⁢ei. Pozostają tylko wyrazy rezonansowe. ∎

Przykład 3.24. Rozważmy przypadek rezonansowego węzła

x˙1=x1+…, ⁢x˙2=n⁢x2+…,

czyli dla λ1=1 i λ2=n∈N∖1 Jak łatwo stwierdzić, jedyną relacją rezonansową jest λ2=n⁢λ1+0⋅λ2. Zatem normalna forma Poincarégo–Dulaca jest następująca

y˙1=y1, ⁢y˙2=n⁢y2+c⁢y1n

(Zadanie 3.30). Okazuje się, że w tym przypadku zamiana prowadząca do postaci normalnej jest analityczna (o ile wyjściowy kiełek był analityczny). ¹³Do tego przypadku można też zaliczyć sytuację, gdy n=1, czyli, gdy część liniowa nie jest diagonalna. Istnieje naturale rozszerzenie Twierdzenia 3.23 na przypadek, gdy część linowa pola posiada nietrywialne klatki Jordana.

Przykład 3.25. Dla siodło–węzła

x˙1=…, ⁢x˙2=x2+…,

czyli z λ1=0 i λ2=1, relacje rezonasowe są postaci λ1=k⁢λ1+0⋅λ2 i λ2=k⁢λ1+1⋅λ2. Stąd wynika następująca forma Poincarégo–Dulaca

y˙1=∑k≥2ak⁢y1k, ⁢y˙2=y2⁢1+∑k≥1bk⁢y1k.

Okazuje się, że na ogół ta forma normalna nie jest analityczna.

Przykład 3.26.Dla 1:-1 rezonansowego siodła

x˙1=x1+…, ⁢x˙2=-x2+…,

czyli z λ1=1 i λ2=-1 relacje rezonansowe są postaci λ1=k+1⁢λ1+k⁢λ2 i λ2=k⁢λ1+k+1⁢λ2. Stąd wynika następująca postać normalna Poincarégo–Dulaca

y˙1=y1⁢1+∑ak⁢y1⁢y2k, ⁢y˙2=-y2⁢1+∑bk⁢y1⁢y2k.

Również i ta forma nie jest na ogól analityczna (Zadanie 3.31).

ZADANIA

Zadanie 3.27. Znaleźć rozmaitość centralną punktu 0,0 dla układu z Zadania 1.33 przy a=-1, tzn. dla x˙=-x+y+x2, y˙=x-y+y2.

Zadanie 3.28. Znaleźć przybliżenie rozmaitości centralnej z dokładnością do wyrazów sześciennych dla punktu 0,0,0 układu x˙=-y+x2+z⁢y, y˙=x+x⁢y+z2, z˙=z+x⁢y.

Zadanie 3.29. Pokazać, że przekształcenie odwrotne do przekształcenia (3.8) ma postać jak w dowodzie Twierdzenia 3.23.

Zadanie 3.30. Pokazać, że w każdym innym przypadku węzła, tzn. gdy 1<λ2/λ1∉N, normalna forma Poincarégo–Dulaca jest liniowa (brak nieliniowych wyrazów rezonansowych).

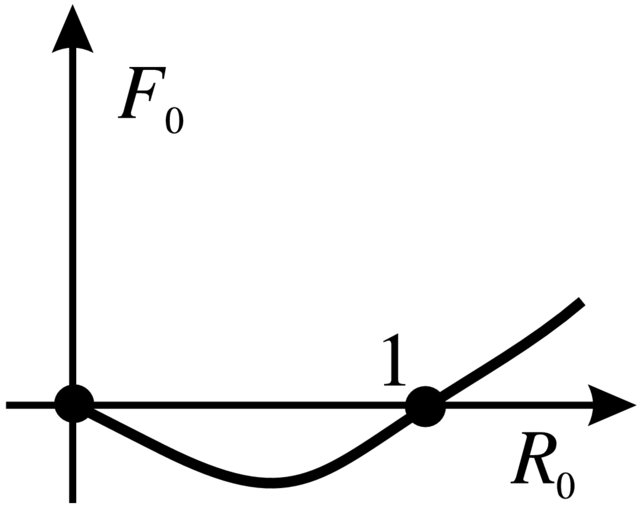
Zadanie 3.31. Uogólnić Przykład 3.26 na przypadek (p:-q)-rezonansowego siodła, tzn. gdy 0<λ1/λ2=-p/q∈Q (ułamek zredukowany).

3.3.2. Bifurkacja siodło–węzeł

Mamy 1-parametrową rodzinę pól wektorowych

x˙=v⁢x;μ=vμ⁢x, ⁢x,μ∈Rn×R,0×0.

Na nią nakładamy następujące warunki:

1. v⁢0;0=0 i v⁢x;0=A⁢x+…

2. Macierz A ma jedną zerową wartość własną, λ1=0, (w szczególności detA=0) i Re⁢λj≠0 dla j>1. Zatem można założyć, że A ma postać blokową

A=000B.

3. Niech x,y będzie liniowym układem współrzędnych związanym z powyższą postacią A. Możemy przepisać układ w postaci

x˙=f⁢x,y;μ, ⁢y˙=B⁢y+…,

gdzie f⁢0,0;0=0 i fx′⁢0,0;0=0, fy′⁢0,0;0=0. Następne założenie mówi, że

∂2⁡f∂⁡x2⁢0,0;0≠0.

4. Ostatnie założenie mówi, że

∂⁡f∂⁡μ⁢0,0;0≠0

(Zadanie 3.34).

Uwaga 3.32. Powyższe warunki są warunkami w przestrzeni J2=J2⁢Rn×R,Rn dżetów rzędu 2. Są to warunki na transwersalność względem pewnych podrozmaitości w J2. Dzięki Twierdzeniu 3.11 typowe v⁢x;μ spełnia te warunki (porównaj też Przykład 3.12).

Rys. 3.11. Bifurkacja siodło–węzeł.

Twierdzenie 3.33.Jeśli są spełnione powyższe warunki, to rodzina vμ jest wersalna. W szczególności, jest ona równoważna jednej z rodzin postaci

x˙=λ±x2, ⁢y˙1=-y1, ⁢y˙2=y2.

Dowód. Z twierdzenia o redukcji do rozmaitości centralnej możemy założyć, że mamy układ postaci

x˙=f⁢x,μ, ⁢y˙1=-y1, ⁢y˙2=y2.

Mamy następujące własności wynikające bezpośrednio z Warunków 1, 2, 3 i 4:

(i) f⁢0,0=0,

(ii) fx′⁢0,0=0,

(iii) fx⁢x′′⁢0,0≠0,

(iv) fμ′⁢0,0≠0.

Dalszy dowód przebiega dokładnie jak w Przykładzie 3.3.

Na Rysunku 3.11 jest przedstawiona bifurkacja siodło–węzeł dla rodziny dwuwymiarowych pól wektorowych. ∎

ZADANIA

Zadanie 3.34. Pokazać, że Warunek 4 posiada następującą interpretację. Z Warunku 3 wynika, że równanie fx′=0 posiada jednoznaczne rozwiązanie x=x0⁢y,μ (punkt lokalnego extremum). Niech g⁢y,μ=f⁢x0⁢y,μ,y;μ (wartość w tego ekstremum). Wtedy ∂⁡f∂⁡μ⁢0,0;0≠0 ⟺ ∂⁡g∂⁡μ⁢0,0≠0.

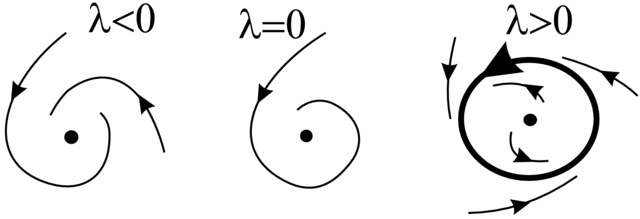
Zadanie 3.35. Dla 2-parametrowej rodziny 1-wymiarowych pól wektorowych x˙=λ1+λ2⁢x+x3 (deformacja osobliwości typu siodło–węzeł kowymiaru 2) zbadać bifurkacje punktów równowagi.

3.3.3. Bifurkacja Andronowa–Hopfa

Mamy 1-parametrową rodzinę pól wektorowych

x˙=v⁢x;μ=vμ⁢x, ⁢x,μ∈Rn×R,0×0.

Na nią nakładamy następujące warunki:

1. v⁢0;0=0, zatem v⁢x;0=A⁢x+…

2. λ1=λ¯2=i⁢ω∈i⁢R∖0 i Re⁢λj≠0 dla j>2. To implikuje det⁡A≠0 i z Twierdzenia o Funkcjach Uwikłanych równanie v⁢x;μ=0 ma rozwiązanie x=x0⁢μ, które odpowiada punktowi równowagi. Następnie przesuwamy ten punkt równowagi do początku układu współrzędnych: x⟼x-x0⁢μ. Teraz mamy układ

x˙=A⁢μ⁢x+….

3. Następne założenie mówi, że

Rys. 3.12. Ostra utrata stabilności.

∂∂⁡μ⁢Re⁢λ1,2⁢μμ=0≠0.

4. Ostatnie założenie wykorzystuje formę normalną Poincarégo–Dulaca dla μ=0. W dziedzinie zespolonej mamy λ1=-λ2 i zgodnie z Przykładem 3.26 forma normalna przyjmuje postać

z˙1=i⁢ω⁢z1⁢1+∑aj⁢z1⁢z2j, ⁢z˙2=-i⁢ω⁢z2⁢1+∑bj⁢z1⁢z2j,

gdzie z1,2=x1±-1⁢x2+…=y1±i⁢y2 są (formalnymi) zmiennymi zespolonymi po ograniczniu do rozmaitości centralnnej. Ponieważ wyjściowe pole było rzeczywiste, to z2=z¯1 i powyższe równania są względem siebie sprzężone. W zmiennych rzeczywistych y1=x1+… i y2=x2+… dostajemy następującą postać normalną Poincarégo–Dulaca dla ogniska

	y˙1	=	y1⁢c3⁢r2+c5⁢r4+…-ω⁢y2⁢1+d3⁢r2+…,
	y˙2	=	ω⁢y1⁢1+d3⁢r2+…+y2⁢c3⁢r2+c5⁢r4+…,

gdzie r2=y12+y22. Tutaj c3,c5,… są liczbami ogniskowymi Lapunowa–Poincarego z Definicji 2.13 (Zadanie 3.40).

Ostatni warunek niezdegenerowania mówi, że

c3≠0.

Następujące twierdzenie nosi też nazwę Twierdzenia o narodzinach cyklu granicznego i jest najbardziej chyba znanym twierdzeniem z teorii bifurkacji.

Twierdzenie 3.36 (Andronov–Hopf). Jeśli są spełnione powyższe warunki, to rodzina vμ jest wersalna. W szczególności jest ona równoważna rodzinie

x˙1=x1⁢λ±r2-ω⁢x2, ⁢x˙2=ω⁢x1+x2⁢λ±r2, ⁢y˙1=-y1, ⁢y˙2=y2,

(r2=x12+x22) lub (równoważnie i na rozmaitości centralnej) rodzinie

z˙=λ+i⁢ω⁢z±z⁢z2, ⁢z=x1+i⁢x2∈C≃R2.

(3.10)

Rys. 3.13. Łagodna utrata stabilności.

Uwaga 3.37. Z dokładnością do zmiany orientacji płaszczyzny (np. (x,y)⟼(x,-y)) można przyjąć, że częstotliwość ω>0. Przy tym założeniu mamy dwie lokalne bifurkacje rodzin (3.10) odpowiadających dwu wartościom c3=1 i c3=-1. Są one przedstawione na Rysunkach 3.12 i 3.13 odpowiednio. Różnica pomiędzy tymi rysunkami ma istotne znaczenie praktyczne.

Na Rysunku 3.12 obserwujemy tzw. ostrą utratę stabilności. Istotnie, dla λ<0 punkt równowagi jest stabilny (chociaż `basen' jego przyciągania kurczy się) a dla λ≥0 punkt równowagi staje się `globalnie' niestabilny (tutaj układ kompletnie się rozstraja).

Na Rysunku 3.13 mamy do czynienia z tzw. łagodną utratą stabilności. Dla μ≤0 punkt równowagi jest `globalnie' stabilny i dla λ>0 traci on stabilność. Ale dla λ>0 pojawia się stabilny cykl graniczny, zlokalizowany blisko punktu równowagi. Zatem układ (np. mechaniczny) zaczyna lekko oscylować wokół położenia równowagi.

Dowód Twierdzenia 3.36. Podobnie jak w przypadku Twierdzenia o Bifurkacji Siodło–Węzeł sprowadzamy najpierw zagadnienie do sytuacji dwuwymiarowej (na rozmaitości centralnej).

Lekko uzupełniając dowód Twierdzenia Poincarégo–Dulaca sprowadzamy całą rodzinę do następującej postaci normalnej, modulo wyrazy rzędu ≥4:

z˙=c1⁢μ+i⁢ω⁢μ⁢z+c3⁢μ+i⁢d3⁢μ⁢z2⁢z+O⁢z4,

(3.11)

z=y1+i⁢y2, gdzie c1⁢0=0, c1′⁢0≠0 i c3⁢0≠0 (Zadanie 3.41). Możemy spokojnie przyjąć, że c1⁢μ=μ, i, przechodząc do biegunowego układu współrzędnych, z=r⁢ei⁢φ, możemy napisać

r˙=r⁢μ+c3⁢r2+O⁢r3, ⁢φ˙=ω+O⁢r2

(3.12)

(Zadanie 3.42).

Rys. 3.14. Dowód Twierdzenia Andronowa–Hopfa.

Dla układu (3.12) definiujemy przekształcenie powrotu Poincarégo P:{φ=0} ⟼{φ=2π} jak na Rysunku 3.14. Dla ustalenia uwagi założymy, że c3=1. Dalszą analizę dzielimy na trzy kroki.

(a) Dla μ≥0 mamy r˙>0 (dla r>0), czyli P⁢r>r i nie ma cykli granicznych.

(b) Niech μ<0. Rozważmy obszar 0≤r≤2⁢-μ. Dokonajmy następującej normalizacji

r=τ⁢R, ⁢μ=-τ2.

Wtedy w obszarze 0≤R≤2 dostajemy układ

R˙=τ2⁢R⁢-1+R2+O⁢τ, ⁢φ˙=ω+O⁢τ

(3.13)

dla małego parametru τ. Teraz już łatwo wyliczyć przekształcenie P.Zauważmy, że rozwiązanie układu (3.13) z warunkiem początkowym R⁢0=R0, φ⁢0=0 spełnia R⁢t=R0+O⁢τ. Zatem

	P⁢R0-R0	=	∫02⁢πd⁢Rd⁢φ⁢d⁢φ=τ2ω⁢∫02⁢πR⁢-1+R2+…1+…⁢d⁢φ
		=	τ2⁢2⁢πω⁢R0⁢R02-1+O⁢τ.

Oznaczmy F⁢R0,τ=P⁢R0-R0/τ2=F0⁢R0+O⁢τ, gdzie wykres funkcji F0R0)=πR0(R02-1)/ω jest przedstawiony na Rysunku 3.15. Widzimy, że równanie F⁢R0,τ=0 posiada dokładnie dwa proste rozwiązania R0=0 i R0=1+O⁢τ (Zadanie 3.43). Pierwsze z nich odpowiada punktowi równowagi, a drugie cyklowi granicznemu bliskiemu okręgu r=-μ.

(c) Dla μ<0 rozważmy obszar 2⁢-μ<r<ε dla małego ε>0 (niezależnego od μ). Z (3.12) łatwo widać, że tutaj r˙>0 i nie może być cykli granicznych.

Rys. 3.15. Wykres funkcji F0.

Widać zatem, że w każdej z trzech powyższych sytuacji portrety fazowe są `jakościowo' takie same jak dla modelowej rodziny (3.10). Wypadałoby jeszcze skonstruować rodzinę hμ lokalnych homeomorfizmów realizujących topologiczne orbitalne równoważności odpowiednich portretów fazowych. Jest to dosyć żmudne zadanie (jeśli potraktować je bardzo serio) i my je opuścimy (nawet w [5] jest to pominięte). ∎

Uwaga 3.38. E. Hopf w swojej oryginalnej pracy udowodnił ogólniejsze wynik niż Twierdzenie 3.36. Mianowicie opuścił on założenie, że c3≠0 (patrz [14]). Pokazał on istnienie 1-parametrowej rodziny γν rozwiązań okresowych dla pól wektorowych vμ⁢ν⁢x, gdzie R+,0∋ν⟶μ⁢ν jest pewnym gładkim odwzorowaniem. To twierdzenie nazywa się Twierdzeniem o Bifurkacji Hopfa. Na przykład, dla rodziny

z˙=μ+i⁢z=vμ⁢z,z¯

mamy rodzinę rozwiązań okresowych γν={|z|2=ν} dla jednego pola z˙=i⁢z=v0⁢z,z¯, tzn. μ⁢ν≡0.

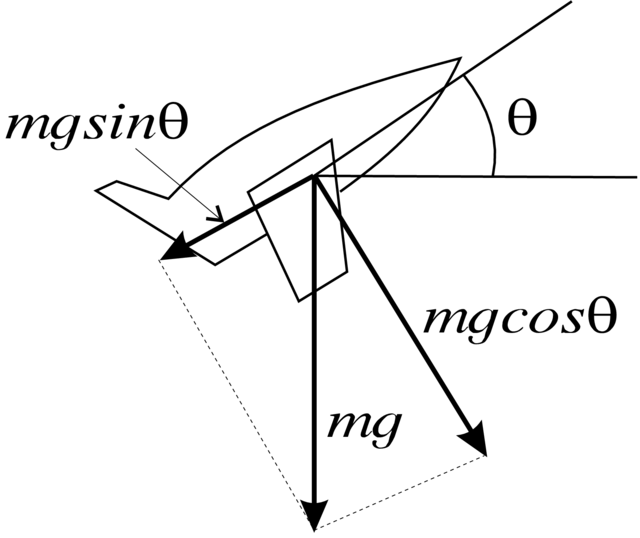
Arnold [5] często podkreślał, że w przypadku c3≠0 odpowiednią bifurkację badał równolegle A. Andronov [2]. Dlatego też bifurkacja z Twierdzenia 3.36 nazywa się Bifurkacją Andronowa–Hopfa.

Rys. 3.16. Szybowiec Żukowskiego.

Przykład 3.39 (Model Żukowskiego szybowca). Niech samolot leci z prędkością v (która może się zmieniać) i jest podniesiony pod kątem θ względem poziomu (patrz Rysunek 3.16). Na samolot działają następujące siły: siła ciągu Fc skierowana wzdłuż samolotu, siła ciężkości m⁢g skierowana do dołu i siła oporu powietrza proporcjonalna do v2. Rozkładamy siłę ciężkości na składową wzdłuż samolotu (powodującą wytracanie prędkości) i w kierunku prostopadłym (powodując obrót w dół). Mamy zatem następującą parę równań: m⁢v˙=Fc-m⁢g⁢sin⁡θ-c2⁢v2 i m⁢v⁢θ˙=-m⁢g⁢cos⁡θ+c2⁢v2. Tutaj stałe c1 i c2 zależą od kilku czynników, których nie będę specyfikował (patrz [8], Rozdz. 3, Paragr. 3) i [7], Rozdz. 14, Paragr. 3, Rozdz. 15, Paragr. 3). Po odpowiedniej normalizacji y=const⋅v dostajemy następującą 2-parametrową rodzinę pól wektorowych

θ˙=y2-cos⁡θ/y, ⁢y˙=λ-μ⁢y2-sin⁡θ,

(3.14)

-π/2≤θ≤π/2, y≥0,z biegunem wzdłuż y=0.

Rozważmy najpierw przypadek λ=0, który odpowiada modelowi szybowca. Po pomnożeniu przez y (przeskalowanie czasu) dostajemy portret fazowy regularnego pola

V=y2-cos⁡θ⁢∂θ-y⁢sin⁡θ+μ⁢y2⁢∂y.

(3.15)

Przy μ=0 dostajemy układ hamiltonowski z całką pierwszą

F=13⁢y3-y⁢cos⁡θ

i punktami równowagi S±=±π/2,0 i C=0,1. Przy μ>0 dostajemy div⁢V=-2⁢μ⁢y<0, czyli funkcja Φ=y jest funkcją Dulaca dla pola (3.14). Stąd łatwo wynika, że dla μ=0 ruch szybowca jest okresowy (oscylujący wokół centrum C) a dla μ>0 odpowiedni punkt krytyczny C (bifurkujący z (0,1)) jest globalnie stabilnym ogniskiem (Zadanie 3.44). To znaczy, że ruch szybowca stabilizuje się.

Dla ogólnej rodziny (3.14) z małymi λ i μ można badać pojawiające się możliwe cykle graniczne metodą całek abelowych (patrz Przykład 4.5 poniżej). Przyrost Δ⁢F całki pierwszej wzdłuż trajektorii układu (3.14) (od cięcia do cięcia) wynosi w przybliżeniu

∫F˙⁢d⁢t=∫y2-cos⁡θ⁢λ-μ⁢y2⁢d⁢t≈∫F=cλ-μ⁢y2⁢y⁢d⁢θ=λ⁢I0⁢c-μ⁢I1⁢c,

gdzie I0⁢c=∫∫d⁢y⁢d⁢x jest polem obszaru zakreślonego przez krzywąF⁢θ,y=c. W [7] pokazano, że funkcja c⟼I1⁢c/I0⁢c jest monotoniczna, czyli, że równanie λ⁢I0⁢c-μ⁢I1⁢c=0 ma co najwyżej jedno rozwiązanie. To oznacza, że układ (4.14) dla małych λ i μ może posiadać co najwyżej jeden cykl graniczny.

Tutaj w momencie, gdy dywergencja pola (3.14) w ognisku C jest zerowa, zachodzi bifurkacja Andronowa–Hopfa. Można sprawdzić, że jest ona niezdegenerowana (zachęcam czytelników do sprawdzenia tego).

ZADANIA

Zadanie 3.40. Pokazać, że współczynniki c3,c5,… z Punktu 4 założeń do Twierdzenia Andronowa–Hopfa pokrywają się ze liczbami oniskowymi Lapunowa–Poincarégo z Definicji 2.13. Znaleźć zależność pomiędzy wspólczynnikami c2⁢j+1 i d2⁢j+1 a aj i bj.

Zadanie 3.41. Udowodnić wzór (3.11).

Wskazówka: Redukcję skończonej liczby wyrazów rezonansowych można przeprowadzać jednocześnie dla 1-parametrowej rodziny.

Zadanie 3.42. Udowodnić wzór (3.12).

Zadanie 3.43. Pokazać ściśle, że równanie F=0 z dowodu Twierdzenia 3.36 ma dokładnie dwa rozwiązania.

Zadanie 3.44. Zbadać punkty osobliwe pola (3.15). Naszkicować portrety fazowe dla μ=0 i μ≠0.

3.3.4. Bifurkacje dla cykli granicznych

Niech γ⊂M będzie zamknniętą krzywą fazową dla pola wektorowego v0⁢x na rozmaitości M (n-wymiarowej). Ponadto pole v0⁢x jest zanurzone w 1-parametrowej rodzinie vμ⁢x, μ∈R,0, pól wektorowych na M. Weźmy cięcie S transwersalne do γ w M. Dla μ bliskich 0 mamy dobrze zdefiniowane przekształcenia Poincarégo Pμ:S⟼S. Utożsamiając S z (Rn-1,0), otrzymujemy rodzinę lokalnych przekształceń

fμ:Rn-1,0⟼Rn-1,0, ⁢fμ⁢z=f⁢z;μ,

takich, że f0⁢0=0. Zatem

Rys. 3.17. Bifurkacja siodło–węzeł dla dyfeomorfizmów.

f0⁢z=A⁢z+…

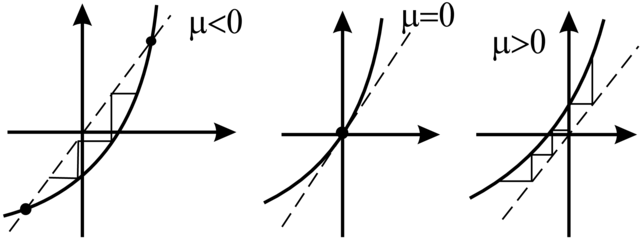
Zakładamy też, że dla μ=0 orbita γ jest niehiperboliczna, tzn. punkt stały z=0 dyfeomorfizmu f0 jest niehiperboliczny. W zależności od typu niehiperboliczności mamy różne rodzaje bifurkacji. My omówimy tutaj tylko dwie.

A. Bifurkacja siodło–węzeł dla cyklu granicznego. Tutaj mamy λ1=1 i λj≠1 j>1 dla wartości własnych macierzy A. Sprowadzając sytuację do rozmaitości centralnej (czyli 1-wymiarowej dla dyfeomorfizmu) i nakładając odpowiednie warunki niezdegenerowania (tzn. ∂2⁡f∂⁡z2⁢0;0⁢∂⁡f∂⁡μ⁢0;0 ≠0), pokazuje się równoważność odpowiedniej rodziny 1-wymiarowych przekształceń z następującą modelową rodziną

f⁢z;μ=x+μ±x2.

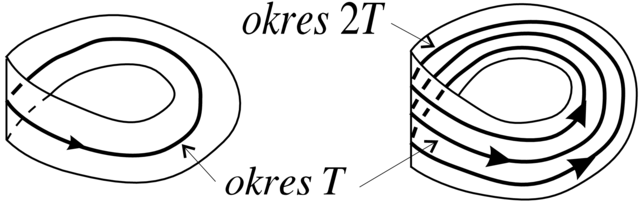
Odpowiednie bifurkacje są przedstawione na Rysunku 3.17. Widzimy, że dla μ<0 mamy dwa cykle graniczne, które się zlewają przy μ=0 a następnie znikają.

B. Bifurkacja podwojenia okresu. Tutaj mamy λ1=-1 i λj≠1 dla j>1. Ponieważ przekształcenie powrotu zmienia orientację, to rozmaitość centralna dla orbity γ jest wstęgą Möbiusa (patrz Rysunek 3.19).

Rys. 3.18. Bifurkacja podwojenia okresu dla dyfeomorfizmów.

Modelową rodziną przekształceń w tym przypadku jest

fμ⁢z=f⁢z,μ=-1+μ⁢z±z3.

Oczywiście to przekształcenie ma tylko jeden punkt stały, tj. z=0. Ale jego druga iteracja ma postać

fμ∘fμ⁢z=1-2⁢μ⁢z∓2⁢z3+…

i posiada dwa dodatkowe punkty stałe z1,2≈∓μ dla ∓μ>0. Te punkty stałe odpowiadają orbicie okresowej dla fμ o okresie 2. Stąd bierze się nazwa bifurkacji; czasami też jest używana nazwa bifurkacja widełki (od kształtu krzywej punktów okresowych na płaszczyźnie (μ,z)).

Odpowiednie bifurkacje dla fμ są przedstawione na Rysunku 3.18.¹⁴Bifurkacja podwojenia okresu leży u podstaw znanej bifurkacji Feigenbauma dla nieodwracalnego przekształcenia g:I⟼I odcinka w siebie. Najpierw punkt stały traci stabilność przy przechodzeniu wartości własnej przez -1. Potem powstała obrita okresowa o okresie 2 znowu traci stabilność i powstaje orbita okresowa o okresie 22, itd. Dla granicznej wartości parametru mamy bifurkację Feigenbauma.

Rys. 3.19. Bifurkacja podwojenia okresu dla cykkli granicznych.

Na tym kończymy omawianie bifurkacji pól wektorowych. Po więcej szczegółów na temat bifurkacji opisanych wyżej i innych bifurkacji odsyłam słuchaczy do literatury ([1], [2], [5], [6], [7], [8], [11], [14]).

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Jakościowa Teoria Równań Różniczkowych Zwyczajnych

Zagadnienia

3. Teoria bifurkacji

3.1. Wersalność

3.2. Transwersalność

3.3. Bifurkacje kowymiaru 1

3.3.1. Redukcja do rozmaitości centralnej i forma normalna Poincarégo–Dulaca

3.3.2. Bifurkacja siodło–węzeł

3.3.3. Bifurkacja Andronowa–Hopfa

3.3.4. Bifurkacje dla cykli granicznych