5.1. Wstęp do teorii chaosu i jeden przykład
Dla autonomicznego pola wektorowego w R2 portret fazowy i ruch
jest w pełni zdeterminowany; to zostało opisane w Rozddziale 2.4. Ale
gdy przestrzeń fazowa nie jest tak prosta, to mogą się zdarzać ciekawe zjawiska.
Na przykład, stałe pole wektorowe
na torusie T2=φ1,φ2 może mieć gęste krzywe fazowe, tj. gdy ω2/ω1 jest niewymierne. Wtedy krzywe fazowe są obmotkami
(jak na Rysunku 4.1 powyżej) a ruch jest prawie okresowy, co
oznacza, że rozwiązanie powraca z grubsza okresowo do każdego małego obszaru przestrzeni fazowej. Ponadto, z każdego małego
obszaru można dojść do dowolnego innego małego obszaru. Taka własność nazywa się tranzytywnością w teorii Układów Dynamicznych. Ruch nie jest w pełni deterministyczny, dlatego
że po długim czasie trudno powiedzieć, gdzie znajduje się
ewoluująca cząstka. Jednak nie jest to ruch chaotyczny, ponieważ, jeśli na początku mieliśmy skupiony obszar przestrzeni
fazowej, to ten obszar zachowuje swój skupiony kształt w trakcie
ewolucji. Tymczasem w ruchu chaotycznym taka komórka zaczyna
`rozpływać się' w przestrzeni fazowej.
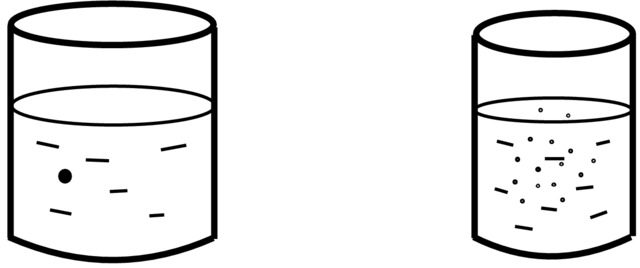
Przykład 5.1 (Tranzytywność i chaos). Dobrym przykładem
sytuacji obrazującej różnicę pomiędzy tranzytywnością a chaosem są dwie szklanki z wodą takie, że w jedną
wpuszczono małą kropelkę oliwy a w drugą wlano taką samą ilość soku (Rysunek 5.1). Kropelka oliwy będzie dryfować, odwiedzająć każde miejsce w wodzie, a sok zacznie się
rozpuszczać, zapełniając równomiernie cały obszar wody (ta własność jest też nazywana mieszaniem).
Chyba najprostszymi układami różniczkowymi, w których można zaobserwować chaos są okresowe nieautonomiczne układy postaci
|
x˙=vt,x, x∈M, vt+T,x=vt,x, |
| (5.1) |
gdzie M jest 2-wymiarową rozmaitością. Jak wiemy, taki układ można potraktować jako autonomiczny w rozszerzonej przestrzeni
fazowej S1×M. Wtedy wygodnie jest pracować z przekształceniem monodromi (po okresie)
gdzie gst jest 2-parametrową rodziną dyfeomorfizmów
definiujących ewolucję. W terminach rozszerzonej przestrzeni
fazowej jest to przekształcenie powrotu na hiperpowierzchnię 0×M.
W monografii J. Guckenheimera i P. Holmes'a [11] jest zanalizowany przykład układu Duffinga z siłą zewnętrzną
My zajmiemy się nieco innym przykładem.
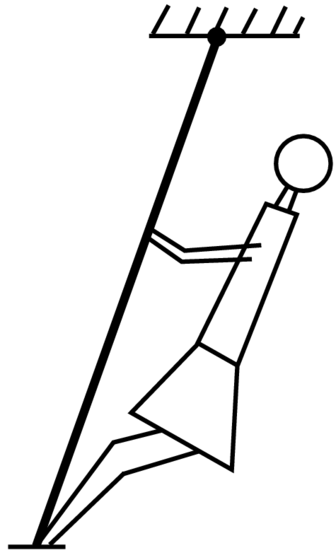
Przykład 5.2 (Huśtawka). Jest to równanie
gdzie εcosωt jest małą okresową siłą zewnętrzną, z okresem T=2π/ω. Można
to interpretować jak równanie huśtawki z dziewczynką, która wykonuje okresowe przykucnięcia (patrz Rysunek 5.2). Można też potraktować ten układ jako podukład 4-wymiarowego układu
autonomicznego
|
x˙=y, y˙=-sinx+εz, z˙=ωu, u˙=-ωz. |
|
Skupmy się jednak na rozszerzonej przestrzeni fazowej S1×M, gdzie M=S1×R jest cylindrem i
mamy
|
t˙=1, x˙=y, y˙=-sinx+εcosωt. |
| (5.2) |
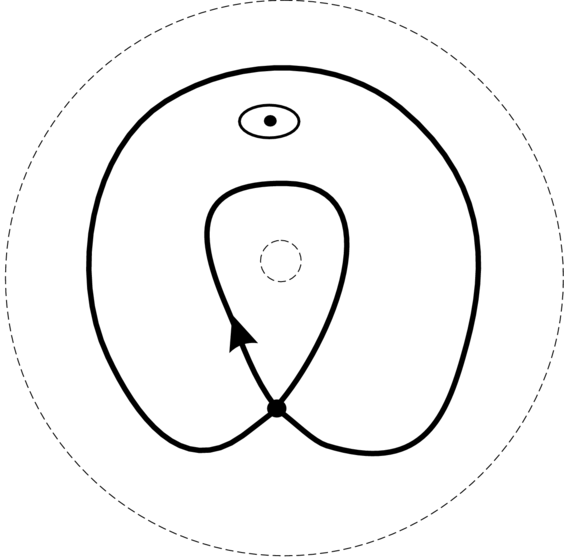
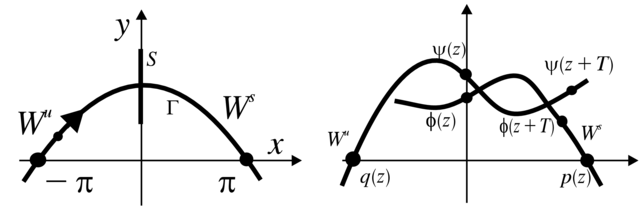
Dla sytuacji niezaburzonej (ε=0) portret fazowy jest znany
(patrz Rysunek 2.1 powyżej); my go przedstawiamy na Rysunku 5.3, gdzie górna i dolna krawędzie walca są przedstawione jako koncentryczne
przerywane okręgi. Nas interesuje, co będzie się działo z pętlą separatrys Γ punktu siodłowego x=π, y=0.
Gdyby zaburzenie było niezależne od czasu, to oczekiwany portret
fazowy zaburzonego pola byłby jak na Rysunku 5.4, czyli separatrysy punktu
siodłowego rozdzieliłyby się. Jednak w przypadku układu
nieautonomicznym, ale okresowym ze względu na czas, portret fazowy układu niezaburzonego należy traktować jako dynamikę przekształcenia monodromii. Przy tym w układzie zaburzonym separatrysy nie mają
obowiązku rozłączyć się. Spodziewamy się, że będą one przecinać się transwersalnie, jak na Rysunku 5.5. Niżej to wykażemy.
Rozwiązanie układu niezaburzonego, odpowiadające górnej pętli separatrys, jest następujące
|
x=x0t=π-4tan-1e-t-t0, y=y0t=2/cosht-t0 |
| (5.3) |
(porównaj Zadanie 2.44). Ma ono tę własność, że xt0=0, yt0=2 i wartość całki pierwszej
wynosi 1 (patrz Rysunek 5.6).
Do badania ukladu zaburzonego (ε≠0) użyjemy całej
rodziny przekształceń monodromii
gdzie M=S1×R jest utożsamiane z cięciem z×M w rozszerzonej przestrzeni fazowej R/T×Z×M. Każde przekształcenie Pz ma swój punkt stały qz (utożsamiany z pz=qz+2π,0; ten punkt zależy od z i od ε i leży blisko punktu x=-π, y=0. Ponieważ jest to punkt stały
i hiperboliczny (siodło) to ma swoją podrozmaitość stabilną
Wspz i niestabilną Wuqz (patrz Rysunek 5.6); oczywiście te podrozmaitości też zależą od z i ε.
Wybierzmy cięcie S={x=0,1<y<3} transwersalne do Wspz i do Wuqz. Niech ϕt (odpowiednio ψ(t)) będzie rozwiązaniem z warunkiem początkowym ϕz=S∩Wspz (odpowiednio ψ(z)=S∩Wu(q(z)))). Oczywiście ϕt→pz przy t→+∞ i ψt→qz przy t→-∞. Ponadto Pzϕz=ϕz+T i Pzψz=ψz+T (niezmienniczość podrozmaitości).
Punkt przecięcia podrozmaitości stabilnej i niestabilnej odpowiada
sytuacji, gdy ϕz=ψz dla odpowiedniego z. Jak w przypadu
autonomicznych zaburzeń układów hamiltonowskich (patrz Przykład
4.5) odległość pomiędzy ϕz i ψz liczymy za
pomocą różnicy wartości całki pierwszej w tych punktach,
|
ΔH|S=H(ψ(z))-H(ϕ(z))={H(ψ(z)-H(q(z))}+{H(p(z))-H(ϕ(z)}. |
|
Mamy
|
H(ψ(z)-H(q(z))=∫-∞zH˙dt=ε∫-∞zycosωtdt,Hpz-Hϕz=∫z∞H˙dt=ε∫z∞ycosωtdt. |
|
Zatem ΔH=ε∫-∞∞ycosωtdt, którą to całkę przybliżmy kładąc y=y0t ze wzoru (5.3). Dostajemy tzw. całkę Mielnikowa
(analog całki abelowej)
|
ΔH=εMz+Oε2=ε⋅2∫-∞∞cosωtcosht-zdt+Oε2. |
| (5.5) |
Nietrudno pokazać następujący
Lemat 5.3.Jeśli Mz0=0 i M′z0≠0, to podrozmaitości Wspz i Wuqz przecinają się transwersalnie w
punkcie bliskimS (Zadanie 5.5).
Okazuje się, że całka Mielnikowa ze wzoru (5.5) jest policzalna.
Podstawiając s=e-t (z ds=-sdt) dostajemy
|
Mz=-2∫0∞eiωzs-iω+e-iωzsiω1+s2ds. |
|
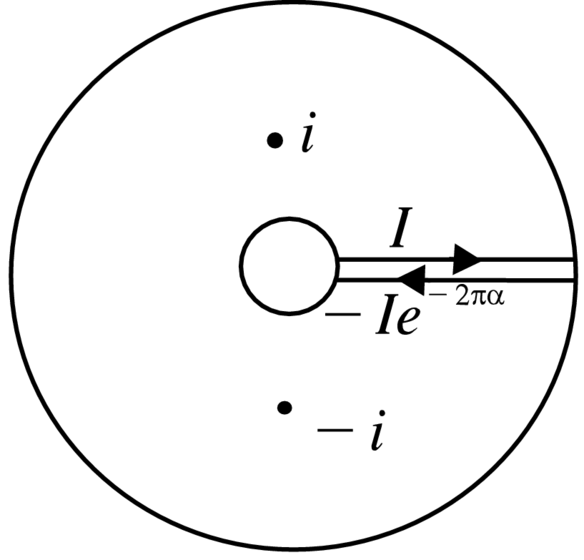
Wyliczymy całkę I=∫0∞siα1+s2-1ds metodą konturową. Całka wzdłuż konturu z
Rysunku 5.7, w granicy z promieniami okręgów dążących do
0 i ∞ odpowiednio, wynosi
|
1-e-2πiαI=2πiress=isiα1+s2-1+ress=-isiα1+s2-1=2πi2ie-πα/2-e-3πα/2=2πe-παsinhπα/2. |
|
To daje I=π/2coshπα/2 i
|
Mz=-2πcosωzcoshπω/2. |
|
Łatwo widać, że ta funkcja spełnia wymaganie M′M=0≠0.
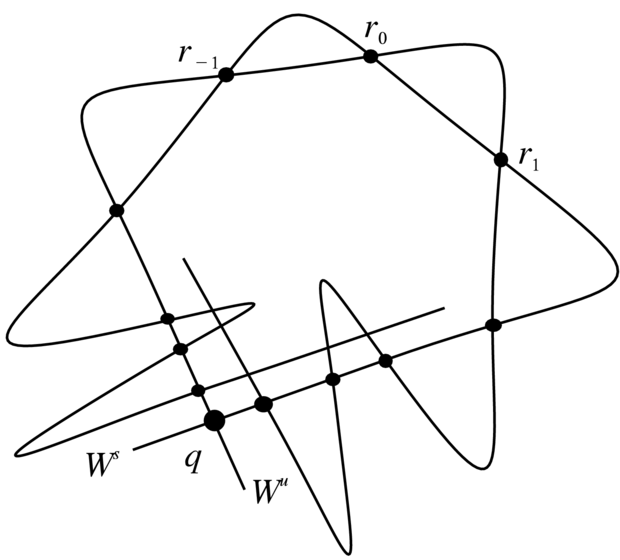
Znaleźliśmy przynajmniej jeden punkt r0 przecięcia się
rozmaitości stabilnej i niestabilnej punktu stałego q=q0 dla
dyfeomorfizmu
gdzie U jest pewnym otoczeniem pętli separatrys Γ siodła x=±π, y=0, a P0 jest wyróżnionym przekształceniem monodromii z rodzimy Pz (z
hiperbolicznymi punktami stałymi q(z)). Ale takich punktów jest
znacznie więcej; są one postaci rn=Pnr0, n∈Z.Przy n→∞ i przy n→-∞
punkty rn dążą do punktu stałego q0.
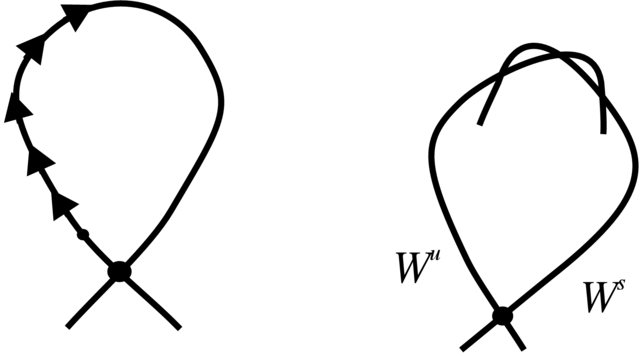
Jednakże podrozmaitości Ws=Wsq0 i Wu=Wuq0 zachowują się co najmniej niestandardowo. Na przykład, rozmaitość Wu przechodząc przez coraz dalsze punkty rnn→∞ zaczyna być coraz bardziej równoległa do
samej siebie, ale w okolicy siodła q (czyli do lokalnej rozmaitości
niestabilnej Wlocu). Przy tym oczywiście, pomiędzy punktami rn i rn+1 wykonuje ostry zakręt. To samo mniej więcej
dzieje się z rozmaitością Ws przyprzejściu
przez punkty rn dla n→-∞ i pomiędzy tymi
punktami. W szczególności wyróżnione powyżej kawałki Wu i Ws zaczynają się przecinać w innych puktach (niż rn). Aż strach pomyśleć, co się dzieje przy
dalszych iteracjach; np. kawałki Wu równoległe do Wlocu zaczynają być coraz dłuższe (patrz Rysunek 5.8).
Zadanie 5.4. Pokazać, że jeśli gst jest 2-parametrową rodziną dyfeomorfizmów definiujących ewolucję
nieautonomicznego pola wektorowego x˙=vt,x, które jest okresowe
z okresem T względem czasu, to gs+Tt+T=gst.
Zadanie 5.5. Udowodnić Lemat 5.3.
Wskazówka: Po pierwsze, pokazać, że (jako bliskie krzywej
fazowej z równania (5.3)) w otoczeniu punktu x=0, y=1 podrozmaitości Wspz i Wuqz leżą poziomo, czyli są
wykresami pewnych funkcji od x. Dla z=z0 będziemy trakować
je jako wykresy funkcji F i G odpowiednio z pewnego odcinka J (na
osi x-ów) do cięcia S, przy czym S jest parametryzowane przez HS.
Po drugie. przekształcenia Pz0 i Pz są sprzężone, Pz=gz0z∘Pz0∘gz0z-1. Wywnioskować stąd, że Wspz=gz0zWspz i podobnie jest z Wu. Przekształcenia gz0z są bliskie przekształceniom g0z-z0ε=0 potoku fazowego niezaburzonego układu (5.2), które w otoczeniu punktu x=0, y=2 jest z grubsza
`ruchem w prawo'. Stąd wynika, że przy zmianie z rozmaitości
Wspz powstają z rozmaitości Wspz0 przez
`przesuwanie' jej. Stąd wynika, że jeśli x0t jest zadane
jak w (5.3), to funkcję H=Fx, której wykresem jest Wspz0, można zadać w pierwszym przybliżeniu jako
Podobnie wykres funkcji Gx≈H∘ψx0-1x w pierwszym przybliżeniu zadaje Wuqz0. Różnica Gx-Fx≈ΔH≈εMz. Pokazać, że
warunek transwersalności Ws i Wu wynika z własności: ddxG-F≠0 dla G-F=0.
5.2. Podkowa Smale'a, dyfeomorfizmy Anosowa i atraktory
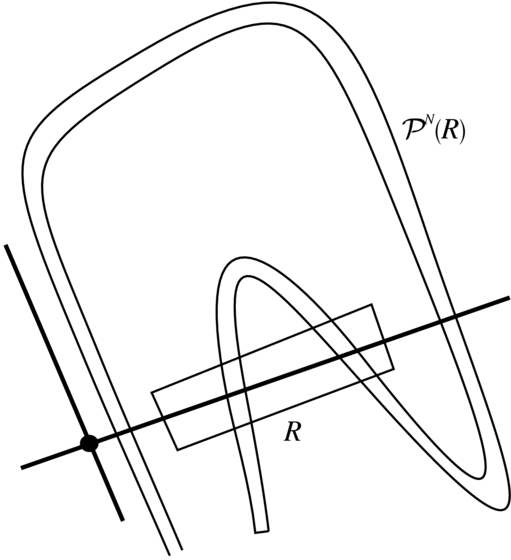
Prawdopodobnie S. Smale był pierwszym, który dobrze zrozumiał zjawisko z końca poprzedniego rozdziału i opisał je w ścisłych matematycznych terminach. Na Rysunku 5.9 widzimy (nieco krzywoliniowy)
`prostokąt ' R wzdłuż lokalnej rozmaitości stabilnej Wlocs, który pod działaniem odpowiednio wysokiej iteracji
przekształcenia P przechodzi na figurę, która
przecina R w dwu miejscach. Można dobrać parametry definiujące
prostokąt R, aby to rzeczywiście miało miejsce; (my tego nie
robimy, ale możemy odesłać czytelnika do książek R.
Devaney'a [9], C. Robinsona [17] i W. Szlenka [18]).
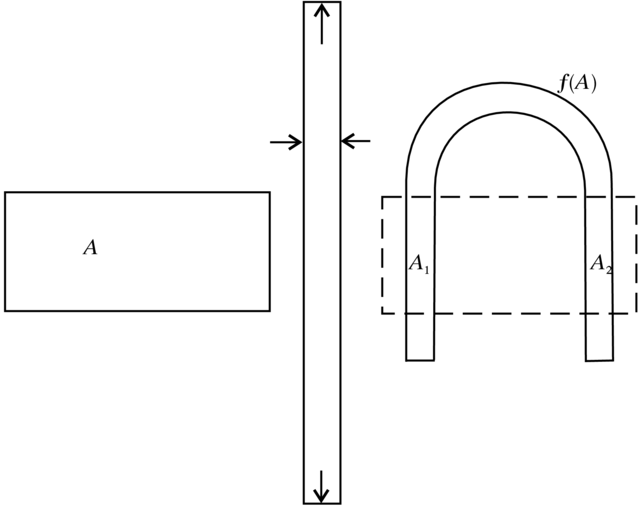
Modelowy przykład przekształcenia jak na Rysunku 5.9 to przekształcenie podkowy Smale'a przedstawione na Rysunku 5.10.
Definicja 5.6 (Podkowa Smale'a). Mamy (autentyczny) prostokąt A na płaszczyźnie, z którym dokonujemy następującej
operacji. Najpierw wydłużmy go w kierunku pionowym i zwężamy w
kierunku poziomym. Następnie zaginamy nasz wydłużony prostokąt
i kładziemy na płaszczyznę tak ,aby przecinał wyjściowy prostokąt wzdłuż dwóch równoległych pionowych pasków
W ten sposób dostajemy nową figurę, oznaczaną fA, gdzie f:A⟼fA jest dyfeomorfizmem podkowy.
Podkowa Smale'a, chociaż prosto zdefiniowana, wcale taka prosta nie
jest. Latwo stwierdzić, że f2A∩A składa się z 4
pionowych pasków; ogólniej, fnA∩A składa się z 2n pionowych pasków (Zadanie 5.14). Z drugiej strony, f-1A∩A=f-1A∩fA składa się z dwu poziomych pasków; ogólniej, f-nA∩A, n>0, składa się z 2n poziomych i
cienkich pasków (Zadanie 5.15). Zatem fnA∩f-mA, m,n>0, składa się z 2n×2m małych prostokącików.
Bardzo ważny jest następujący zbiór
Łatwo sprawdzić, że jest to zbiór niezmienniczy względem f: fΛ=f-1Λ=Λ (Zadanie 5.16). Można
powiedzieć więcej o Λ i o fΛ, ale najpierw
powinniśmy wprowadzić jedną definicję.
Definicja 5.7. Niech Σ=Σk=1,…,kZ będzie przeliczalnym iloczynem kartejańskim ustalonego zbioru k-elementowego; składa się ona z ciągów a=…,a-1,a0,a1,…, aj∈1,…,k. Zdefiniujemy przekształcenie σ:Σ⟼Σ następująco:
Układ dynamiczny Σ,σ zdefiniowany powyżej
nazywa się układem symbolicznym, albo przesunięciem.
Na przetrzeni Σ wprowadza się topologię produktową,
gdzie otoczeniami danego ciągu symboli a=…,a-1,a0,a1,… są zbiory cylindryczne
postaci
|
b=…,b-1,b0,b1,…:b-M=a-M,b-M+1=a-M+1,…,bN=aN |
|
(dla ustalonych M,N). Σ jest też przestrzenią metryczna,
bo odległość dwóch ciągów to dista,b=∑n∈Z2-nan-bn.
Twierdzenie 5.8.Istnieje ciągły homeomorfizm Φ:Λ⟼Σ2, który sprzęga σ zf|Λ:
Dowód. Przekształcenie Φ jest łatwe do
zdefiniowania. Jeśli x∈Λ, to kładziemy Φx=…,a-1,a0,a1,…, gdzie
|
an=1 gdy fnx∈A1 i an=2 gdy fnx∈A2. |
|
Własność sprzęgania sprawdza się bezpośrednio (Zadanie
5.18). Pozostaje zatem tylko sprawdzić ciągłość i
odwracalność przekształcenia Φ.
Te dwie własności wynikają z hiperboliczności przekształcenia podkowy: w kierunku poziomym jest ściskanie ze stałą λ1<1 a w kierunku pionowym mamy rozciąganie ze stałą λ1>1. Zatem prostokąciki, pojawiające się przy
lokalizacji punktów x, tzn.
|
x:f-Mx∈Aa-M,…,fNx∈AaN, |
| (5.7) |
stają się eksponencjalnie małe przy M i N bardzo dużych. W
granicy dostaniemy tylko jeden punkt (odwracalność). Małe rozmiary
zbiorów (5.7) odpowiadają małości odpowiednich zbiorów
cylindrycznych w Σ; jest to dokładnie ciągłość Φ i Φ-1. ∎
Ponieważ Λ jest jedynym zbiorem niezmienniczym w prostokącie A, to cała interesująca dynamika przekształcenia podkowy
ogranicza się do dynamiki fΛ. Dzięki powyższemu
twierdzeniu jest to taka sama dynamika, jak dla przekształcenia
symbolicznego σ na Σ. Z drugiej strony, przekształcenie
symboliczne jest przyjemne do badania. Ma ono następujące ciekawe włsności.
Stwierdzenie 5.9.Punkty okreowe dla σ są gęste w przestrzeni symbolicznejΣ.
Dowód. Niech a=…,a-1,a0,a1,…∈Σ. Dla dużego N>0 wszyskie ciągib=…,b-1,b0,b1,… takie, że b-N=a-N,…,bN=aN są bliskie a. Zatem bliski jest też ciąg utworzony z bloku a-N,…,aN (długości 2N+1) i powtarzanego periodycznie. Odpowiada on puktowi
okresowemu dla σ o okresie 2N+1. ∎
Stwierdzenie 5.10.Układ dynamiczny Σ,σ jest tranzytywny, tzn. dla dowolnych podzbiorów otwartych U,V⊂Σ istnieje i n>0 takie, żefnU∩V≠∅.
Dowód. Wystarczy rozważyć przypadek, gdy U i V są zbiorami cylindrycznymi definiowanymi przy pomocy bloków a1,…,aM i b1,…,bN. Wtedy
wystaczy wziąć dowolny ciąg z blokiem a1,…,aM,b1,…bN (długości M+N). ∎
Uwaga 5.11. Można wprowadzić na Σ probabilistyczną miarę produktową μ, taką, że μ({a0=j})=1/k (miara Bernoulliego). Okazuje się ona być niezmiennicza względem przesunięcia σ. Ponadto
zachodzi własność mieszania, o której wspomniałem na początku rozdziału a której nie chcę ściśle definiować. Zatem układ podkowy Smale'a a także układ huśtawki są układami chaotycznymi.
Podzbiór Λ⊂R2, niezmienniczy dla przekształcenia podkowy Smale's, ma jeszcze jedną ważną własność. Mianowicie jest hiperboliczny, co oznacza, że indukowane
przekształcenia liniowe f∗x:TxR2⟼TfxR2 są hiperboliczne (mają jedną wartość własną λ1∈0,1 i drugą λ2>1).
Niestety, zbiór Λ jest bardzo cienki (jego wymiar Hausdorffa
zależy od λ1 i λ2) i na pewno nie jest rozmaitością (nawet lokalnie). Ale istnieją chaotyczne układy
dynamiczne ze strukturą hiperboliczną na całej rozmaitości. Są to tzw. dyfeomorfizmy Anosowa, których najbardziej znanym
reprezentatnem jest następujący
Przykład 5.12 (Hiperboliczny automorfizm torusa). Utożsamijmy
dwuwymiatowy torus z płaszczyzną podzieloną przez kratę, T2=R2/Z2. Macierz
zadaje przekształcenie płaszczyzny, które punkty o współrzędnych całkowitych przekształca na podobne punkty. Zatem definiuje ono
przekształcenie f:T2⟼T2. Ponieważ
wyznacznik naszej macierzy jest równy 1, to i przekształcenie odwrotne
zachowuje kratę; zatem f jest dyfeomorfizmem.
Przekształcenie f ma dokładnie jeden punkt stały, odpowiadający
punktowi 0,0. Za to równania na punkty okresowe o
okresie 2 przyjmują postać 4x1+3x2=m1, 3x1+x2=m2, m1,2∈Z. Nietrudno zobaczyć, że daje to 25 rozwiązań. Ogólnie, ze wzrostem n liczba punktów okresowych dla f o okresie ≤n rośnie do nieskończoności; w szczególności, punkty z wymiernymi obiema współrzędnymi są okresowe (Zadanie 5.19).
Macierz pochodnej f∗x:TxT2⟼TfxT2 w każdym punkcie x jest taka sama i równa A. Z
kolei macierz A jest hiperboliczna, z wartościami własnymi λ1=123-5<1 i λ2=123+5>1. Zatem f ma (równomierną) strukturę hiperboliczną. (Ta własność wchodzi w definicję dyfeomorfizmu Anosowa, której nie przytaczam).
Co więcej, przez każdy punkt x∈T2 przechodzą
dwie specjalne krzywe: jedna Wsx odpowiada prostej w kierunku własnym odpowiadającym λ1, i druga Wux odpowieda
prostej w drugim kierunku własnym. Ponieważ wartości własne są niewymierne, to współczynniki nachylenia obu kierunków własnych są niewymierne. Zatem każda z rozmaitości Wsx i Wux jest gęsta w torusie (tworzy obmotkę); w topologii mówi się o podrozmaitościach immersyjnych.
Okazuje się, że hiperboliczny automorfizm torusa ma własność tranzytywności mieszania względem miary Lebesque'a (która jest zachowana przez f).
Na koniec, poinformuję czytelników, że dyfeomorfizm f jest
strukturalnie stabilny. To znaczy, że dowolny bliski niemu dyfeomorfizm g jest z nim sprzężony przy pomocy pewnego homeomorfizmu torusa h (analog Twierdzenia Grobmana–Hartmana). Jest to ogólna własność dyfeomorfizmów Anosowa.
Innym naturalny układem typu Anosowa jest potok geodezyjny na powierzchni o stałej ujemnej krzywiźnie.
Bardzo ważnymi przykładami układów dynamicznych są tzw.
atraktory hiperboliczne. Są to przekształcenia gładkie
(nawet niekoniecznie odwracalne) f:M⟼M dla których istnieje
domknięty podzbiór niezmienniczy Λ⊂M z otoczeniem U⊃Λ takim, że Λ=⋂n≥0fnU.
Lokalnie Λ ma postać N×C, gdzie N jest regularną
rozmaitością (z 0<dimN<dimM) a C jest zbiorem typu Cantora.
Ponadto Λ ma strukturę hiperboliczną w tym sensie, że f∗x jednostajnie rozciąga w kierunku N i jednostajnie
ściska w kierunku transwersalnym do N.
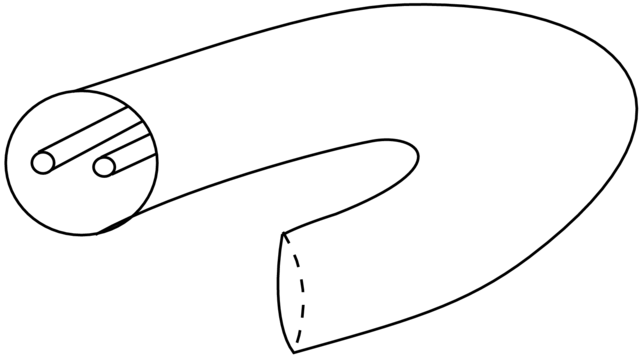
Przykład 5.13 (Selenoid). Niech M=D2×S1=z,y będzie pełnym torusem, gdzie
D2=z:z≤1⊂C
to dysk a S1=y mod Z. Przekształcenie jest zadane następująco
|
f:z,y⟼14z+12e2πiy,2y mod Z. |
|
Obrazem fM⊂M będzie torus czterokrotnie cieńczy i
dwukrotnie dłuższy oraz włożony w M tak, że owija się
dwukrotnie wokół `równika' M przy tym lekko skręcając
(patrz Rysunek 5.11).
Oczywiście Λ=⋂n≥0fnM jest zbiorem
niezmienniczym i spełnia wymagania, które nałożyłem powyżej na hiperboliczne atraktory.
Na koniec, chciałbym zauważyć, że w teorii układów
dynamicznych trudny do rozwiązania problem stanowią tzw. dziwne atraktory, które spełniają własność Λ=⋂n≥0fnU, ale nie chcą być równomiernie
hiperboliczne. Najbardziej znane to atraktor Hènona zadany
odwzorowaniem
(gdzie np. a=1.4 i b=0.3) i atraktor Lorenza zadany polem
wektorowym
|
x˙=-σx+σy, y˙=-xz+rx-y, z˙=xy-bz |
|
(gdzie np. σ=10, r-28 i b=8/3).
Zadanie 5.14. Narysować f2A.
Zadanie 5.15. Pokazać, że f-nA∩A, n>0, składa się z 2n poziomych pasków.
Zadanie 5.16. Udowodnić, że Λ ze wzoru (5.6) jest
zbiorem niezmienniczym.
Zadanie 5.17. Pokazać, że Λ (z (5.6)) jest
homeomorficzne z C×C, gdzie C jest (odpowiednio zdefiniowanym)
zbiorem Cantora.
Zadanie 5.18. Sprawdzić, że Φ sprzęga f z σ.
Zadanie 5.19. Udowodnić, że zbiór punktów
okresowych przekształcenia z Przykładu 5.12 pokrywa się ze zbiorem
punktów o wymierych obu współrzędnych.
Wskazówka: Zbiór pN,qN mod Z2: p,q∈N
dla ustalonego N∈N jest skończony i niezmienniczy względem f. Ponadto równania na punkty okresowy o okresie n przyjmują
postać An-Ix=m, gdzie m=m1,m2∈Z2.