Zagadnienia

1.1 Zmienne ilościowe
- 1.1.1 Miary rozrzutu
- 1.1.2 Miary zależności
1.2 Zmienne porządkowe
- 1.2.1 Miary zależności
1.3 Zmienne jakościowe
1.4 Przykłady w programie R

1. Miary zależności i miary bliskości między zmiennymi

W rozdziale tym przedstawione zostaną wskaźniki liczbowe do analizy danych jedno- i dwuwymiarowych. Przypomniane zostaną miary rozrzutu oraz omówione miary zależności i miary bliskości między zmiennymi (cechami).

Główna różnica:

miary zależności: minimalne dla zmiennych niezależnych, maksymalne dla zmiennych identycznych;
miary bliskości (odległości, zróżnicowania): minimalne dla zmiennych identycznych;

Wygodnie jest podzielić zmienne na ilościowe (liczbowe), porządkowe i jakościowe (nominalne). Miary wprowadzone dla danych liczbowych, wykorzystujące wartości liczbowe, mają zastosowanie tylko dla nich. Miary dla zmiennych porządkowych nadają się również dla zmiennych liczbowych, ponieważ otrzymujemy je przez zamianę wartości cechy na kolejne liczby naturalne $1,2,\ldots,n$ lub ułamki jednostajnie rozłożone na odcinku $[0,1]$ , czyli $\frac{i}{n}-\frac{1}{2n}$ , gdzie $i=1,2,\ldots,n$ . Miary dla zmiennych jakościowych są oparte na gęstościach i mają zastosowanie do wszystkich zmiennych.

Miary zależności i bliskości zostaną podzielone na symetryczne i niesymetryczne (zależność czy błąd nie muszą być relacjami symetrycznymi). Podsumowanie znajduje się w poniższej tabelce:

	Zmienne ilościowe	Zmienne porządkowe	Zmienne jakościowe
Miary zależności	Korelacja	Korelacja rang,	Wspólna
symetryczne		Współczynnik Kendalla	Informacja
Miary zależności			Współczynnik
niesymetryczne			Goodmana-Kruskala
Miary odległości	Błąd średniokwadratowy
symetryczne	$\mathbb{E}(X-Y)^{2}$
Miary odległości	$\frac{\mathbb{E}(X-Y)^{2}}{\mathbb{E}Y^{2}}$		$\chi^{2}(p,q)$ ,
niesymetryczne			$\text{H}(p\|\|q)$

W dalszej części skryptu będziemy oznaczać wielkimi literami, np. $X$ , $Y$ zarówno zmienne losowe jak i ich realizacje. Rozróżnienie będzie wynikać z kontekstu.

Definicja 1.1

Próbą będziemy nazywali $n$ realizacji zmiennej losowej: $X=(X_{1},\ldots,X_{n})$ .

Średnią z próby będziemy oznaczać jako:

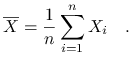$\overline{X}=\frac{1}{n}\sum _{{i=1}}^{n}X_{i}\quad.$

1.1. Zmienne ilościowe

Dla zmiennych ilościowych możemy zdefiniować kwantyle:

Definicja 1.2

Kwantyl rzędu $p$ , $p$ $\in$ $(0,1)$ :

$\varphi _{p}(X)=F_{X}^{{-1}}(p)=\inf\{ x:F_{X}(x)\geq p\},$

gdzie $F_{X}$ oznacza dystrybuantę. Kwantyle rzędu $\frac{1}{4},\frac{1}{2},$ i $\frac{3}{4}$ nazywamy kwartylami, z czego kwantyl rzędu $\frac{1}{2}$ to mediana.

Estymatorami kwantyli dla próby $X=(X_{1},\ldots,X_{n})$ są kwantyle próbkowe.

Definicja 1.3

Kwantyle próbkowe rzędu $p$ dla próby n-elementowej, $p$ $\in$ $(0,1)$ :

$\widehat{\varphi}_{p}(X)=\frac{1}{2}(X_{{\lfloor p(n+1):n\rfloor}}+X_{{\lceil p(n+1):n\rceil}}),$

gdzie $X_{{k:n}}$ oznacza $k$ -ty element statystyki pozycyjnej: po uszeregowaniu niemalejąco wartości $X_{i}\quad i=1,\ldots,n,\quad X_{{k:n}}$ oznacza $k$ -tą wartość z $n$ -elementowego ciągu. Funkcja ceiling zwraca najmniejszą liczbę całkowitą mniejszą od danej, a funkcja floor największą liczbę całkowitą mniejszą.

1.1.1. Miary rozrzutu

Wariancja:

wersja populacyjna

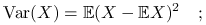
$\text{Var}(X)=\mathbb{E}(X-\mathbb{E}X)^{2}\quad;$

wersja próbkowa

$\text{var}(X)=\frac{1}{n}\sum _{{i=1}}^{n}(X_{i}-\overline{X})^{2}\quad;$

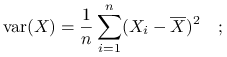
wersja próbkowa nieobciążona

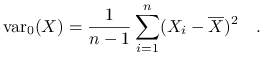
$\text{var}_{0}(X)=\frac{1}{n-1}\sum _{{i=1}}^{n}(X_{i}-\overline{X})^{2}\quad.$
Odchylenie standardowe:

wersja populacyjna

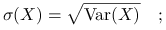
$\sigma(X)=\sqrt{\text{Var}(X)}\quad;$

wersja próbkowa

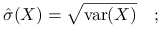
$\hat{\sigma}(X)=\sqrt{\text{var}(X)}\quad;$

wersja próbkowa niebciążona

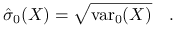
$\hat{\sigma}_{0}(X)=\sqrt{\text{var}_{0}(X)}\quad.$
MAD (Median of Absolute Deviation):

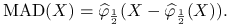
$\text{MAD}(X)=\widehat{\varphi}_{{\frac{1}{2}}}(X-\widehat{\varphi}_{{\frac{1}{2}}}(X)).$

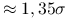Dla rozkładu normalnego, MAD $\approx 1,35\sigma$ .
IQR (Interquartile Range)

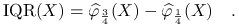
$\text{IQR}(X)=\widehat{\varphi}_{{\frac{3}{4}}}(X)-\widehat{\varphi}_{{\frac{1}{4}}}(X)\quad.$

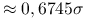Dla rozkładu normalnego IQR $\approx 0,6745\sigma$ .

1.1.2. Miary zależności

Korelacja pomiędzy zmiennymi 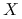$X$ i $Y$ :

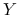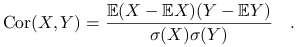
$\text{Cor}(X,Y)=\frac{\mathbb{E}(X-\mathbb{E}X)(Y-\mathbb{E}Y)}{\sigma(X)\sigma(Y)}\quad.$

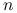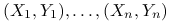Dla próby $n$ -elemnentowej: $(X_{1},Y_{1}),\ldots,(X_{n},Y_{n})$ korelacja próbkowa:

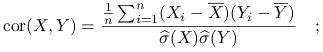
$\text{cor}(X,Y)=\frac{\frac{1}{n}\sum _{{i=1}}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\widehat{\sigma}(X)\widehat{\sigma}(Y)}\quad;$

korelacja próbkowa nieobciążona:

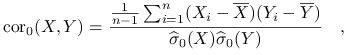
$\text{cor}_{0}(X,Y)=\frac{\frac{1}{n-1}\sum _{{i=1}}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\widehat{\sigma}_{0}(X)\widehat{\sigma}_{0}(Y)}\quad,$

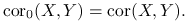
$\text{cor}_{0}(X,Y)=\text{cor}(X,Y).$

1.2. Zmienne porządkowe

Zmienne porządkowe to takie, dla których nie są ważne wartości, ale kolejność, w jakiej są ustawione. Z pojęciem zmiennej porządkowej ściśle wiąże się pojęcie rangi. Nadanie rang obserwacjom uniezależnia je od skali.

Definicja 1.4

Rangi dla obserwacji w próbie $X=(X_{1},\ldots,X_{n})$ :

$R_{i}=R(X_{i})=\#\{ j:X_{j}<X_{i}\}+\frac{1+\#\{ j:X_{j}=X_{i}\}}{2}\quad.$

Przykład 1.1

Dla $X=(2;3;2,5;2,5;1,5)$ rangi są równe:

X	2	3	2,5	2,5	1,5
R	2	5	3,5	3,5	1

1.2.1. Miary zależności

Korelacja rang (Spearmana):

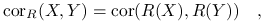
$\text{cor}_{R}(X,Y)=\text{cor}(R(X),R(Y))\quad,$

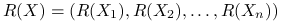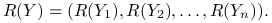
gdzie $R(X)=(R(X_{1}),R(X_{2}),\ldots,R(X_{n}))$ , $R(Y)=(R(Y_{1}),R(Y_{2}),\ldots,R(Y_{n})).$

Stwierdzenie 1.1

Załóżmy, że $X,Y$ mają rozkłady o ciągłych i ściśle rosnących dystrybuantach. Wtedy:

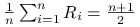$\frac{1}{n}\sum _{{i=1}}^{n}R_{i}=\frac{n+1}{2}$ ;
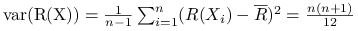$\text{var(R(X))}=\frac{1}{n-1}\sum _{{i=1}}^{n}(R(X_{i})-\overline{R})^{2}=\frac{n(n+1)}{12}$ ;
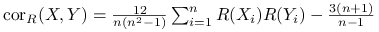$\text{cor}_{R}(X,Y)=\frac{12}{n(n^{2}-1)}\sum _{{i=1}}^{n}R(X_{i})R(Y_{i})-\frac{3(n+1)}{n-1}$ ;
$\text{cor}_{R}(X,Y)\xrightarrow[n\rightarrow\infty]{p.n}\text{Cor}(F_{X}(X),F_{Y}(Y))$ ;
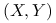Jeżeli $(X,Y)$ ma 2-wymiarowy rozkład normalny,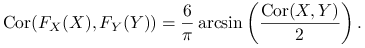

$\text{Cor}(F_{X}(X),F_{Y}(Y))=\frac{6}{\pi}\arcsin\left(\frac{\text{Cor}(X,Y)}{2}\right).$

Współczynnik Kendala zależności między 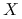$X$ a $Y$ :

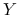Załóżmy, że 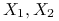$X_{1},X_{2}$ to zmienne losowe niezależne i o takim samym rozkładzie co 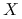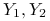$X$ , $Y_{1},Y_{2}$ niezależne o takim samym rozkładzie co 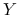$Y$ . Niech:

$X_{{12}}=\left\{\begin{array}[]{ll}1,&\hbox{$X_{1}>X_{2}$ ;}\\ 0,&\hbox{$X_{1}=X_{2}$ ;}\\ -1,&\hbox{$X_{1}<X_{2}$ .}\end{array}\right.\quad Y_{{12}}=\left\{\begin{array}[]{ll}1,&\hbox{$Y_{1}>Y_{2}$ ;}\\ 0,&\hbox{$Y_{1}=Y_{2}$ ;}\\ -1,&\hbox{$Y_{1}<Y_{2}$ .}\end{array}\right.$

$\tau _{k}(X,Y)=\text{Cor}(X_{{12}},Y_{{12}})=$

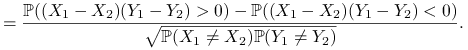$=\frac{\mathbb{P}((X_{1}-X_{2})(Y_{1}-Y_{2})>0)-\mathbb{P}((X_{1}-X_{2})(Y_{1}-Y_{2})<0)}{\sqrt{\mathbb{P}(X_{1}\neq X_{2})\mathbb{P}(Y_{1}\neq Y_{2})}}.$

Jeśli $X,Y$ mają ciągłe dystrybuanty, to

$\tau _{k}(X,Y)=\mathbb{P}((X_{1}-X_{2})(Y_{1}-Y_{2})=1)-\mathbb{P}((X_{1}-X_{2})(Y_{1}-Y_{2})=-1).$

Wersja próbkowa $\tau _{k}$ :

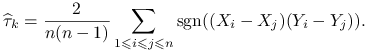$\widehat{\tau}_{k}=\frac{2}{n(n-1)}\sum _{{1\leq i\leq j\leq n}}\text{sgn}((X_{i}-X_{j})(Y_{i}-Y_{j})).$

Uwaga 1.1

W programie R: cor(X, Y, method = c(”pearson”, ”kendall”, ”spearman”)) z domyślnie ustawioną opcją ”pearson”.

1.3. Zmienne jakościowe

W tej części omówione zostaną miary rozrzutu, zależności i bliskości oparte na gęstościach prawdopodobieństwa, wykorzystywane przede wszytkim do analizy cech jakościowych.

1.3.1. Miary rozrzutu

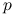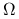Entropia dla gęstości $p$ o nośniku $\Omega$ :

$\text{H}(p)=-\int _{{\Omega}}[\ln p(v)]p(v)dv.$

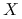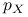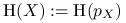Jeśli $X$ - zmienna losowa o gęstości $p_{X}$ , to $\text{H}(X):=\text{H}(p_{X})$ .

Uwaga 1.2

Różnice i podobieństwa między H $(X)$ i Var $(X)$ :

Załóżmy, że 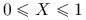$0\leq X\leq 1$ . Wtedy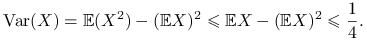

$\text{Var}(X)=\mathbb{E}(X^{2})-(\mathbb{E}X)^{2}\leq\mathbb{E}X-(\mathbb{E}X)^{2}\leq\frac{1}{4}.$

Zatem wariancja jest największa dla rozkładu dwupunktowego: 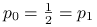$p_{0}=\frac{1}{2}=p_{1}$ . Entropia natomiast jest największa dla rozkładu jednostajnego.
Załóżmy teraz, że 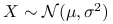$X\sim\mathcal{N}(\mu,\sigma^{2})$ . Mamy: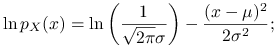

$\ln p_{X}(x)=\ln\left(\frac{1}{\sqrt{2\pi}\sigma}\right)-\frac{(x-\mu)^{2}}{2\sigma^{2}};$

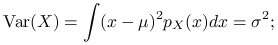
$\text{Var}(X)=\int(x-\mu)^{2}p_{X}(x)dx=\sigma^{2};$

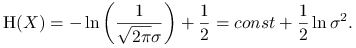
$\text{H}(X)=-\ln\left(\frac{1}{\sqrt{2\pi}\sigma}\right)+\frac{1}{2}=const+\frac{1}{2}\ln\sigma^{2}.$

Współczynnik Giniego dla gęstości $p$ :

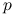$\text{V}(p)=\int _{{\Omega}}[1-p(v)]p(v)dv=1-\int _{{\Omega}}p^{2}(v)dv.$

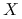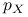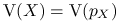Jeśli $X$ - zmienna losowa o gęstości $p_{X}$ , to $\text{V}(X)=\text{V}(p_{X})$ .

V(p) jest liniowym (rozwinięcie Taylora dla logarytmu naturalnego: 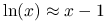$\ln(x)\approx x-1$ ) przybliżeniem H(p).

1.3.2. Miary bliskości

Dla prostoty ograniczymy się w dalszej części wykładu do rozkładów dyskretnych zadanych gęstościami $p$ i $q$ o wspólnym nośniku $\Omega$ .

Odległość Kullbacka-Leiblera (względna entropia):

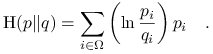
$\text{H}(p||q)=\sum _{{i\in\Omega}}\left(\ln\frac{p_{i}}{q_{i}}\right)p_{i}\quad.$

Stwierdzenie 1.2

Własności Odległości Kullbacka-Leiblera (entropii względnej):

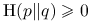$\text{H}(p||q)\geq 0$ ;
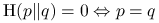$\text{H}(p||q)=0\Leftrightarrow p=q$ .

Skorzystajmy z nierówności: $\ln(x)\leq x-1$ :

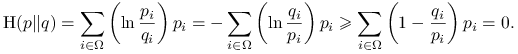$\text{H}(p||q)=\sum _{{i\in\Omega}}\left(\ln\frac{p_{i}}{q_{i}}\right)p_{i}=-\sum _{{i\in\Omega}}\left(\ln\frac{q_{i}}{p_{i}}\right)p_{i}\geq\sum _{{i\in\Omega}}\left(1-\frac{q_{i}}{p_{i}}\right)p_{i}=0.$

Stąd otrzymujemy $(1).$ Równość w ostatniej nierówności jest równoważna warunkowi $\frac{q_{i}}{p_{i}}=1$ dla wszystkich $i$ , otrzymujemy $(2).$

∎

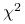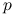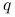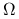Odległość $\chi^{2}$ między rozkładami dyskretnymi zadanymi gęstościami $p$ i $q$ o wspólnym nośniku $\Omega$ :

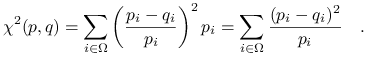
$\chi^{2}(p,q)=\sum _{{i\in\Omega}}\left(\frac{p_{i}-q_{i}}{p_{i}}\right)^{2}p_{i}=\sum _{{i\in\Omega}}\frac{(p_{i}-q_{i})^{2}}{p_{i}}\quad.$ (1.1)

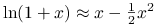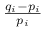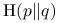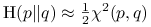Odległość $\chi^{2}$ jest kwadratowym (rozwinięcie Taylora dla logarytmu: $\ln(1+x)\approx x-\frac{1}{2}x^{2}$ , gdzie za $x$ wstawiamy $\frac{q_{i}-p_{i}}{p_{i}}$ ) przybliżeniem $\text{H}(p||q)$ : $\text{H}(p||q)\approx\frac{1}{2}\chi^{2}(p,q)$ .

1.3.3. Miary zależności

Niech $X,Y$ będą zmiennymi o rozkładzie dyskretnym, niekoniecznie o tym samym nośniku $\Omega$ . Ponadto zdefiniujmy:

$p_{{ij}}=\mathbb{P}(X=i,Y=j)$ ;

$p_{{j|i}}=\mathbb{P}(Y=j|X=i)$ ;

$p_{{i.}}=\mathbb{P}(X=i)$ ;

$p_{{.j}}=\mathbb{P}(Y=j)$ ;

warunkowy współczynnik Giniego $\text{V}(Y|X=i)=1-\sum _{{j}}p^{2}_{{j|i}}$ ;

warunkową entropię $\text{H}(Y|X=i)=-\sum _{{j}}(\ln p_{{j|i}})p_{{j|i}}$ .

Zauważmy, że:

$\mathbb{E}\text{V}(Y|X)=\sum _{{i}}\text{V}(Y|X=i)p_{{i.}}=1-\sum _{{i}}p_{{i.}}\sum _{{j}}p^{2}_{{j|i}};$

$\mathbb{E}\text{H}(Y|X)=\sum _{{i}}\text{H}(Y|X=i)p_{{i.}}.$

Współczynnik Goodmana-Kruskala (mówi on o tym, jak zmienił się rozrzut po zaobserwowaniu cechy $X$ ):

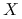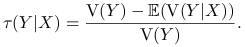
$\tau(Y|X)=\frac{\text{V}(Y)-\mathbb{E}(\text{V}(Y|X))}{\text{V}(Y)}.$

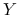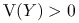Zakładamy, że rozkład $Y$ jest niezdegenerowany, czyli że $\text{V}(Y)>0$ .

Stwierdzenie 1.3

Własności Współczynnika Goodmana-Kruskala:

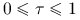$0\leq\tau\leq 1$ ;
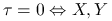$\tau=0\Leftrightarrow X,Y$ niezależne.

Oczywiście $\tau\leq 1$ . Dla dowodu, że $\tau\geq 0$ zauważmy, że $\mathbb{E}\text{V}(Y|X)=1-\sum _{{i}}p_{{i.}}\sum _{{j}}p^{2}_{{j|i}}.$ Wystarczy pokazać, że $\sum _{{j}}p^{2}_{{.j}}\leq\sum _{{j}}\sum _{{i}}p_{{i.}}p^{2}_{{j|i}}$ . Z kolei wystarczy pokazać, że $p^{2}_{{.j}}\leq\sum _{{i}}p_{{i.}}p^{2}_{{j|i}}$ . Lewa $=p^{2}_{{.j}}=(\sum _{{i}}p_{{ij}})^{2}=(\sum _{{i}}p_{{j|i}}p_{{i.}})^{2}$ , więc $(1)$ wynika z nierówności Jensena.

Dla dowodu $(2)$ zauważmy, że ,,=” w nierówności Jensena wyrazów $p_{{j|i}}=p_{{.j}}$ $\forall i,j$ jest równoważna niezależności $X,Y$ .

∎

Wspólna informacja zawarta w 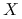$X$ i $Y$ :

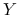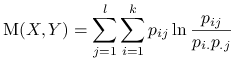
$\text{M}(X,Y)=\sum _{{j=1}}^{l}\sum _{{i=1}}^{k}p_{{ij}}\ln\frac{p_{{ij}}}{p_{{i.}}p_{{.j}}}$

Stwierdzenie 1.4

Własności Wspólnej informacji:

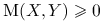$\text{M}(X,Y)\geq 0$ ;
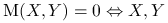$\text{M}(X,Y)=0\Leftrightarrow X,Y$ niezależne.

Wynika z własności odległości Kullbacka-Leiblera (stwierdzenie 1.2), bo $\text{M}(X,Y)=H(p_{{ij}}||(p_{{i.}}p_{{.j}}))$

∎

Uwaga 1.3

Korzystając z przybliżenia rozwinięciem w szereg Taylora logarytmu: $\ln(1+x)\approx x-\frac{1}{2}x^{2}$ , otrzymujemy:

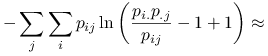	$\displaystyle\text{M}(X,Y)=$	$\displaystyle-\sum _{j}\sum _{i}p_{{ij}}\ln\left(\frac{p_{{i.}}p_{{.j}}}{p_{{ij}}}-1+1\right)\approx$
	$\displaystyle=$	$\displaystyle-\left[\sum _{{ji}}\left(\frac{p_{{i.}}p_{{.j}}}{p_{{ij}}}-1\right)p_{{ij}}-\frac{1}{2}\sum _{{ji}}\left(\frac{p_{{i.}}p_{{.j}}}{p_{{ij}}}-1\right)^{2}p_{{ij}}\right]=$
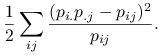	$\displaystyle=$	$\displaystyle\frac{1}{2}\sum _{{ij}}\frac{(p_{{i.}}p_{{.j}}-p_{{ij}})^{2}}{p_{{ij}}}.$

Ostatnie wyrażenie oraz statystyka $\chi^{2}=\sum _{{ij}}\frac{(p_{{ij}}-p_{{i.}}p_{{.j}})^{2}}{p_{{i.}}p_{{.j}}}$ dla testowania niezależności mają podobną interpretację, chociaż różnica w treści matematycznej jest zasadnicza. Być może o podobieństwie wyrażeń decydują własności błędu względnego: jeśli błąd względny oszacowania $a$ za pomocą $b$ jest nie większy od $\varepsilon$ , to błąd względny oszacowania $b$ za pomocą $a$ jest nie większy niż $\frac{\varepsilon}{1-\varepsilon}$ . Przy małym $\varepsilon$ wyrażenia te są porównywalne.

Uwaga 1.4

Wspólna informacja dla rozkładu dwuwymiarowego normalnego, gdzie $(X,Y)\sim\mathcal{N}\left(\left(\begin{array}[]{c}\mu _{X}\\ \mu _{Y}\\ \end{array}\right),\left(\begin{array}[]{cc}\sigma^{2}_{X}&\rho\sigma _{X}\sigma _{Y}\\ \rho\sigma _{X}\sigma _{Y}&\sigma _{Y}^{2}\\ \end{array}\right)\right)$ , jest równa:

$\text{M}(X,Y)=-\ln\sqrt{1-\rho^{2}},$

gdzie $\rho=\text{Cor}(X,Y)$ .

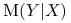Jeżeli zamiast współczynnika Giniego we wzorze na współczynnik Goodmana-Kruskala użyjemy entropii, otrzymamy analogiczny współczynnik $\text{M}(Y|X)$ :

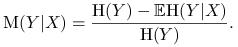
$\text{M}(Y|X)=\frac{\text{H}(Y)-\mathbb{E}\text{H}(Y|X)}{\text{H}(Y)}.$

Stwierdzenie 1.5

$\text{M}(Y|X)=\frac{\text{H}(Y)-\mathbb{E}\text{H}(Y|X)}{\text{H}(Y)}=\frac{\text{M}(X,Y)}{\text{H}(Y)}.$

	$\displaystyle\mathbb{E}\text{H}(Y\|X)$	$\displaystyle=-\sum _{i}p_{{i.}}\sum _{j}p_{{j\|i}}\ln p_{{j\|i}}=-\sum _{{ij}}p_{{ij}}\ln p_{{j\|i}}=$
		$\displaystyle=-\left[\sum _{{ij}}p_{{ij}}\ln p_{{ij}}-\sum _{{ij}}p_{{ij}}\ln p_{{i.}}\right]=$
		$\displaystyle=\text{H}(X,Y)+\sum _{{i}}\ln p_{{i.}}\sum _{j}p_{{ij}}=\text{H}(X,Y)+\sum _{{i}}\ln p_{{i.}}\cdot p_{{i.}}=$
		$\displaystyle=\text{H}(X,Y)-\text{H}(X),$

gdzie $\text{H}(X,Y)=\text{H}(P_{{(X,Y)}})$ .

Zatem $\text{M}(Y|X)=\frac{\text{H}(X)+\text{H}(Y)-\text{H}(X,Y)}{\text{H}(Y)}$ .

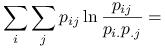	$\displaystyle\text{M}(X,Y)=$	$\displaystyle\sum _{i}\sum _{j}p_{{ij}}\ln\frac{p_{{ij}}}{p_{{i.}}p_{{.j}}}=$
	$\displaystyle=$	$\displaystyle\sum _{i}\sum _{j}p_{{ij}}\ln p_{{ij}}-\sum _{i}\sum _{j}p_{{ij}}\ln(p_{{i.}}p_{{.j}})=$
	$\displaystyle=$	$\displaystyle-\text{H}(X,Y)-\sum _{i}\sum _{j}p_{{ij}}\ln p_{{i.}}-\sum _{j}\sum _{i}p_{{ij}}\ln p_{{.j}}=$
	$\displaystyle=$	$\displaystyle-\text{H}(X,Y)-\sum _{i}\ln(p_{{i.}})p_{{i.}}-\sum _{j}\ln(p_{{.j}})p_{{.j}}=$
	$\displaystyle=$	$\displaystyle-\text{H}(X,Y)+\text{H}(X)+\text{H}(Y).$