11. Opcje amerykańskie i egzotyczne w modelu Blacka-Scholesa
11.1. Opcje amerykańskie
Celem tego paragrafu jest podanie podstawowych rezultatów dotyczących opcji amerykańskich w modelu Blacka-Scholesa. Jak wiemy, opcje te dają posiadaczowi prawo do wykonania opcji w dowolnej chwili, dlatego analogicznie jak w przypadku rynku skończonego trzeba zastosować inne podejście niż w przypadku opcji europejskich.
Zaczniemy od definicji opcji amerykańskiej. Niech ![]() będzie funkcją ciągłą.
będzie funkcją ciągłą.
Definicja 11.1
Opcją amerykańską ![]() american contingent claim
american contingent claim![]() z funkcją wypłaty
z funkcją wypłaty ![]() nazywamy
instrument finansowy określony przez:
nazywamy
instrument finansowy określony przez:
-
a) moment wygaśnięcia
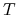 ,
, -
b) wypłatę w chwili
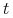 równą
równą 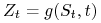 ,
,
-
c) moment realizacji opcji — jest to moment stopu
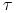 względem filtracji
względem filtracji 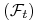 przyjmujący wartości w
przyjmujący wartości w ![[0,T]](wyklady/ip1/mi/mi1035.png) , a
zatem wypłata w momencie realizacji jest równa
, a
zatem wypłata w momencie realizacji jest równa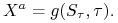
(11.1)
Wymiennie z terminem opcja amerykańska z funkcją wypłaty ![]() będziemy używać terminu opcja amerykańska z procesem wypłaty
będziemy używać terminu opcja amerykańska z procesem wypłaty ![]() lub opcja amerykańska o wypłacie
lub opcja amerykańska o wypłacie ![]() .
.
Intuicyjnie, moment wykonania opcji amerykańskiej bazuje na
informacji o cenach. O tym, czy wykonać opcję w momencie ![]() decydujemy obserwując ceny do chwili
decydujemy obserwując ceny do chwili ![]() . Dlatego moment wykonania
jest momentem stopu i jest elementem rodziny
. Dlatego moment wykonania
jest momentem stopu i jest elementem rodziny ![]() ,
czyli rodziny momentów stopu o wartościach w
,
czyli rodziny momentów stopu o wartościach w ![]() (to uzasadnia
założenie
(to uzasadnia
założenie ![]() w definicji). Wypłata zależy od wartości akcji
w definicji). Wypłata zależy od wartości akcji
![]() w chwili realizacji, a nie od całej trajektorii
w chwili realizacji, a nie od całej trajektorii ![]() do
momentu
do
momentu ![]() (stąd założenie (11.1) w definicji).
Typowe przykłady opcji amerykańskich to opcja kupna o wypłacie
w chwili realizacji:
(stąd założenie (11.1) w definicji).
Typowe przykłady opcji amerykańskich to opcja kupna o wypłacie
w chwili realizacji:
a także opcja sprzedaży o wypłacie w chwili realizacji:
Zatem funkcja wypłaty dla amerykańskiej opcji kupna ma postać
![]() , a dla amerykańskiej opcji sprzedaży ma
postać
, a dla amerykańskiej opcji sprzedaży ma
postać ![]() . Często dopuszcza się, że cena wykonania
opcji zmienia się wraz z czasem, ale jest funkcją deterministyczną,
tj.
. Często dopuszcza się, że cena wykonania
opcji zmienia się wraz z czasem, ale jest funkcją deterministyczną,
tj. ![]() , wtedy np. zmodyfikowana
amerykańska opcja kupna ma wypłatę postaci
, wtedy np. zmodyfikowana
amerykańska opcja kupna ma wypłatę postaci
tj. ![]() . Jest to przykład tzw. niestandardowej
amerykańskiej opcji kupna (nonstandard american call option).
Są to opcje, dla których warunki wczesnej realizacji są nietypowe.
Przykładowo, cena realizacji może zależeć od czasu i tak np. dla
5-letniej opcji kupna cena wykonania
. Jest to przykład tzw. niestandardowej
amerykańskiej opcji kupna (nonstandard american call option).
Są to opcje, dla których warunki wczesnej realizacji są nietypowe.
Przykładowo, cena realizacji może zależeć od czasu i tak np. dla
5-letniej opcji kupna cena wykonania ![]() może wynosić 50 przez
pierwszy rok, 55 przez drugi i trzeci, a 60 w ostatnich dwu.
może wynosić 50 przez
pierwszy rok, 55 przez drugi i trzeci, a 60 w ostatnich dwu.
Celem tego paragrafu jest znalezienie racjonalnej ceny i sensownego
momentu wykonania opcji amerykańskiej za pomocą argumentów
arbitrażowych. Dla prostoty zapisu skoncentrujemy się na momencie
![]() .
.
Przez strategię ,,kup i trzymaj” (buy-and-hold) związaną z opcją
amerykańską o wypłacie ![]() rozumiemy parę
rozumiemy parę ![]() ,
,
![]() ,
, ![]() . Interpretacja tej
strategii jest następująca: gdy
. Interpretacja tej
strategii jest następująca: gdy ![]() , to kupujemy
, to kupujemy ![]() jednostek
opcji amerykańskiej w chwili 0, a gdy
jednostek
opcji amerykańskiej w chwili 0, a gdy ![]() to przeprowadzamy krótką
sprzedaż tych jednostek w chwili 0 i trzymamy je w portfelu do
momentu
to przeprowadzamy krótką
sprzedaż tych jednostek w chwili 0 i trzymamy je w portfelu do
momentu ![]() , w którym zamykamy pozycję.
, w którym zamykamy pozycję.
Definicja 11.2
Strategia samofinansująca się dla modelu ![]() to trójka
to trójka
![]() , gdzie
, gdzie ![]() jest strategią samofinansująca
się w modelu Blacka-Scholesa, a
jest strategią samofinansująca
się w modelu Blacka-Scholesa, a ![]() jest strategią ,,kup
i trzymaj”
związaną z
jest strategią ,,kup
i trzymaj”
związaną z ![]() i taką, że dla
i taką, że dla ![]() zachodzi
zachodzi
W definicji strategii samofinansującej się zakładamy, że gdy
wypłata amerykańska jest realizowana w momencie ![]() , to pozycja
w aktywie jest w tym momencie zamykana i wszystko co pozostaje, jest
wkładane na rachunek oszczędnościowy.
, to pozycja
w aktywie jest w tym momencie zamykana i wszystko co pozostaje, jest
wkładane na rachunek oszczędnościowy.
Przypomnijmy, że strategia ![]() jest
samofinansującą się w modelu Blacka-Scholesa, gdy proces bogactwa
jest
samofinansującą się w modelu Blacka-Scholesa, gdy proces bogactwa
![]() spełnia
spełnia
Wprowadziliśmy nowy instrument bazowy, którym możemy handlować na
rynku, opcje amerykańskie. Gdy oznaczymy przez ![]() liczbę
opcji w portfelu, to strategię ,,kup
i trzymaj”
zapiszemy wzorem
liczbę
opcji w portfelu, to strategię ,,kup
i trzymaj”
zapiszemy wzorem ![]() .
.
Gdy ![]() jest wartością w chwili 0 opcji amerykańskiej z wypłatą
jest wartością w chwili 0 opcji amerykańskiej z wypłatą
![]() , to wartości portfela
, to wartości portfela ![]() w momencie początkowym
i końcowym wynoszą:
w momencie początkowym
i końcowym wynoszą:
| (11.2) | |||||
| (11.3) |
Mówimy, że portfel samofinansującej się ![]() jest
dopuszczalny, gdy
jest
dopuszczalny, gdy ![]() jest strategią dopuszczalną. Klasę
strategii dopuszczalnych oznaczymy przez
jest strategią dopuszczalną. Klasę
strategii dopuszczalnych oznaczymy przez ![]() . Definiujemy klasę
portfeli arbitrażowych:
. Definiujemy klasę
portfeli arbitrażowych:
Równoważnie jest to klasa portfeli dopuszczalnych ![]() ,
takich że
,
takich że
bo istnieje rachunek oszczędnościowy ze stopą procentową ![]() .
.
Definicja 11.3
Na rynku ![]() z ceną początkową
z ceną początkową ![]() wypłaty
wypłaty
![]() istnieje arbitraż, gdy zachodzi jeden z warunków
istnieje arbitraż, gdy zachodzi jeden z warunków ![]() ,
, ![]() :
:
-
a) istnieje arbitraż związany z pozycją długą (tj. posiadacza opcji amerykańskiej), czyli gdy istnieje moment stopu
![\tau\in{\cal T}_{{[0,T]}}](wyklady/ip1/mi/mi2008.png) taki, że dla pewnego
taki, że dla pewnego 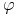 strategia
strategia
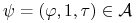 ,
,
-
b) istnieje arbitraż związany z pozycją krótką (tj. wystawcy opcji amerykańskiej), czyli gdy istnieje
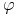 strategia taka,
że dla wszystkich momentów stopu
strategia taka,
że dla wszystkich momentów stopu ![\tau\in{\cal T}_{{[0,T]}}](wyklady/ip1/mi/mi2008.png) strategia
strategia 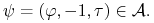
Gdy nie istnieje arbitraż, to mówimy, że model jest wolny od arbitrażu.
Te dwa rodzaje arbitrażu wynikają z niesymetrycznej pozycji sprzedawcy i nabywcy opcji amerykańskiej. Nabywca może wybrać termin wykonania, a sprzedawca musi zabezpieczyć wypłatę.
Z definicji wynika, że na rynku nie ma arbitrażu, gdy zachodzą dwa warunki:
a) dla wszystkich ![]() i wszystkich
i wszystkich ![]() mamy
mamy ![]() ,
,
oraz
b) dla każdego ![]() istnieje
istnieje ![]() takie, że
takie, że ![]()
Punkt a) mówi, że posiadacz opcji amerykańskiej nie może znaleźć
momentu wykonania opcji ![]() i strategii
i strategii ![]() działania na
rynku akcji i rachunku bankowego dających zysk bez ryzyka. Natomiast
punkt b) oznacza, że niezależnie od tego, jaką politykę prowadzi
sprzedawca opcji (czyli niezależnie od
działania na
rynku akcji i rachunku bankowego dających zysk bez ryzyka. Natomiast
punkt b) oznacza, że niezależnie od tego, jaką politykę prowadzi
sprzedawca opcji (czyli niezależnie od ![]() ), nabywca może
wybrać taki moment wykonania
), nabywca może
wybrać taki moment wykonania ![]() , że sprzedawca nie ma zysku bez
ryzyka.
, że sprzedawca nie ma zysku bez
ryzyka.
Definicja 11.4
Ceną arbitrażową opcji amerykańskiej ![]() nazywamy cenę
nazywamy cenę ![]() , dla której opisany model rynku jest modelem
wolnym od arbitrażu.
, dla której opisany model rynku jest modelem
wolnym od arbitrażu.
Okazuje się, że założenie braku arbitrażu prowadzi do istnienia jednoznacznie wyznaczonej ceny arbitrażowej.
Twierdzenie 11.1
Niech ![]() będzie funkcją o liniowym
wzroście (czyli spełniającą warunek
będzie funkcją o liniowym
wzroście (czyli spełniającą warunek ![]() . Załóżmy,
że na rynku
. Załóżmy,
że na rynku ![]() nie ma możliwości arbitrażu. Wtedy
cena arbitrażowa w chwili
nie ma możliwości arbitrażu. Wtedy
cena arbitrażowa w chwili ![]() opcji amerykańskiej z funkcją wypłaty
opcji amerykańskiej z funkcją wypłaty
![]() jest równa:
jest równa:
| (11.4) |
gdzie ![]() jest miarą martyngałową dla rynku Blacka-Scholesa
jest miarą martyngałową dla rynku Blacka-Scholesa
![]() .
.
Przypomnijmy, że supremum istotne rodziny zmiennych losowych ![]() jest to jedyna zmienna losowa
jest to jedyna zmienna losowa
![]() (ozn.
(ozn. ![]() )
o własnościach:
)
o własnościach:
-
a)
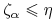
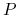 -p.n. dla każdego
-p.n. dla każdego 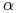 ,
, -
b) jeśli
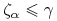
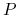 -p.n. dla każdego
-p.n. dla każdego 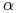 , to
, to
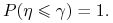
Idea dowodu tw. 11.1 jest analogiczna do idei dowodu
twierdzenia podającego cenę arbitrażową wypłaty amerykańskiej dla
modelu z czasem dyskretnym. Korzysta się z ogólnych faktów z teorii
optymalnego stopowania. Gdy ![]() jest
zdyskontowanym procesem wypłaty, to dowodzimy, że obwiednia Snella
procesu
jest
zdyskontowanym procesem wypłaty, to dowodzimy, że obwiednia Snella
procesu ![]() , czyli najmniejszy nadmartyngał majoryzujący
, czyli najmniejszy nadmartyngał majoryzujący ![]() ,
jest postaci
,
jest postaci
i daje nam cenę arbitrażową ![]() . Ponadto moment wykonania zadany
jest wzorem:
. Ponadto moment wykonania zadany
jest wzorem:
W szczególności
a optymalny moment wykonania
Szczegóły techniczne można znaleźć w Myneni [Myn], Karatzas [Kar]. Warto zauważyć, że zachodzi też twierdzenie odwrotne: warunek
implikuje, że na rynku ![]() nie ma możliwości
arbitrażu (patrz ćw. 11.2).
nie ma możliwości
arbitrażu (patrz ćw. 11.2).
Można udowodnić (patrz ćw. 11.1), że istnieje portfel
dopuszczalny ![]() , spełniający warunki:
, spełniający warunki: ![]() i
i
| (11.5) |
czyli ![]() jest portfelem zabezpieczającym opcję amerykańską
z kapitałem początkowym równym cenie opcji amerykańskiej. Dla tego
portfela zachodzi
jest portfelem zabezpieczającym opcję amerykańską
z kapitałem początkowym równym cenie opcji amerykańskiej. Dla tego
portfela zachodzi
Ze wzoru (11.4) wynika, analogicznie jak w przypadku
dyskretnym, że cena opcji amerykańskiej o wypłacie ![]() jest nie mniejsza niż cena opcji europejskiej o wypłacie
jest nie mniejsza niż cena opcji europejskiej o wypłacie ![]() .
Ponadto
.
Ponadto
Twierdzenie 11.2
Europejska opcja kupna i standardowa amerykańska opcja kupna o tym samym terminie zapadalności i tej samej cenie wykonania mają równe ceny.
Załóżmy, że ![]() (dla
(dla ![]() dowód jest analogiczny). Niech
dowód jest analogiczny). Niech
![]() , gdzie
, gdzie ![]() Wtedy z (11.4)
Wtedy z (11.4)
zatem by zakończyć dowód trzeba pokazać nierówność przeciwną.
Wystarczy pokazać, że dla dowolnego momentu stopu ![]() zachodzi:
zachodzi:
| (11.6) |
gdyż stąd ![]() .
Ponieważ
.
Ponieważ ![]() jest
jest ![]() -martyngałem,
-martyngałem, ![]() ,
, ![]() , więc
, więc
Prawa strona jest nieujemna, więc stąd
Biorąc wartość oczekiwaną obu stron otrzymujemy (11.6).
∎Uwaga 11.1
Warto prześledzić inne rozumowanie prowadzące do tego wyniku.
Gdy ![]() , to z parytetu dla cen opcji europejskich
, to z parytetu dla cen opcji europejskich
więc wartość amerykańskiej opcji kupna w chwili ![]() jest większa niż
zysk z jej realizacji w chwili
jest większa niż
zysk z jej realizacji w chwili ![]() , czyli nie opłaca się realizować
opcji przed jej wygaśnięciem.
, czyli nie opłaca się realizować
opcji przed jej wygaśnięciem.
Z tw. 11.2 wynika, że dla znalezienia ceny amerykańskiej opcji kupna możemy korzystać ze wzoru Blacka-Scholesa na cenę europejskiej opcji kupna.
W przypadku opcji sprzedaży cena amerykańska opcji jest różna od ceny europejskiej. Ma różne dobre własności, ale nie istnieje postać jawna ceny amerykańskiej opcji sprzedaży. Do wyliczenia tej ceny stosuje się inne metody: metody Monte Carlo, metody quasi Monte Carlo, metody aproksymacji modelem CRR lub metody numeryczne związane z rozwiązywaniem równań różniczkowych cząstkowych.
11.2. Opcje egzotyczne
Są to opcje inne niż standardowe opcje kupna/sprzedaży europejskie i amerykańskie (które z kolei nazywa się opcjami waniliowymi). Zatem opcje egzotyczne mają funkcje wypłaty inne niż funkcje wypłaty związane z opcjami waniliowymi. Nie zawsze znajdują się one w obrocie giełdowym, są raczej opcjami na zamówienie (over the counter options). Są oferowane przez instytucje finansowe dla swoich klientów. Opiszemy przykładowo kilka najczęściej pojawiających się rodzajów takich opcji. Wyceny tych opcji pozostawimy jako zadanie (często bardzo trudne, jak w przypadku opcji azjatyckich).
1. Niestandardowe opcje amerykańskie, które opisaliśmy w poprzednim paragrafie.
2. Opcje bermudzkie (Bermudan options). Są to opcje,
które mogą być realizowane tylko w pewne dni (zatem opcje te,
obrazowo mówiąc, tworzą pomost pomiędzy opcjami europejskimi
i amerykańskimi). Można je traktować jako specyficzny rodzaj opcji
amerykańskich, dla których funkcja wypłaty ![]() dla tych chwil
dla tych chwil
![]() , kiedy opcji nie możemy zrealizować.
, kiedy opcji nie możemy zrealizować.
3. Opcje startujące w przyszłości (forward start
options). Niech ![]() . W chwili
. W chwili ![]() jedna strona
kontraktu otrzymuje opcję z terminem wygaśnięcia
jedna strona
kontraktu otrzymuje opcję z terminem wygaśnięcia ![]() i ceną
wykonania
i ceną
wykonania ![]() i płaci za to drugiej stronie w chwili zero.
Przykładowo, dla opcji kupna startującej w przyszłości wypłata
wynosi
i płaci za to drugiej stronie w chwili zero.
Przykładowo, dla opcji kupna startującej w przyszłości wypłata
wynosi ![]()
4. Opcje wyboru (chooser options, as-you-like-it
options). Opcja, której właściciel w określonej chwili ![]() w przyszłości ma prawo zdecydować czy chce, żeby była to opcja
sprzedaży czy kupna (czas realizacji
w przyszłości ma prawo zdecydować czy chce, żeby była to opcja
sprzedaży czy kupna (czas realizacji ![]() i cena wykonania
i cena wykonania ![]() są
określone z góry w momencie sprzedaży opcji). Właściciel opcji
w chwili
są
określone z góry w momencie sprzedaży opcji). Właściciel opcji
w chwili ![]() wybiera opcję o większej wartości, stąd wartość tej
opcji w chwili
wybiera opcję o większej wartości, stąd wartość tej
opcji w chwili ![]() wynosi
wynosi
co pozwala łatwo ją wycenić.
5. Opcje binarne (binary options). Są to opcje, których
wypłata zależy w sposób nieciągły od ceny instrumentu pierwotnego
![]() w momencie wykonania opcji
w momencie wykonania opcji ![]() .
.
Przykład 11.1
a) Opcja pieniądze albo nic (opcja cash or nothing).
Dla tej opcji wypłata ![]() w chwili wygaśnięcia
w chwili wygaśnięcia ![]() wynosi:
wynosi:
— dla binarnej opcji kupna ![]() ,
,
— dla binarnej opcji sprzedaży ![]() ,
,
gdzie stałe ![]() i
i ![]() zostały ustalone z góry.
zostały ustalone z góry.
b) Opcja walor albo nic (opcja asset or nothing).
Dla tej opcji wypłata ![]() w chwili wygaśnięcia
w chwili wygaśnięcia ![]() wynosi:
wynosi:
— dla opcji kupna ![]() ,
,
— dla opcji sprzedaży ![]() ,
,
gdzie stała ![]() została ustalone z góry.
została ustalone z góry.
Zauważmy, że opcje powyższe można porównać do zakładu, czy cena
waloru jest większa czy nie od z góry ustalonego progu ![]() . Opcja
kupna daje niezerową wypłatę, gdy cena instrumentu pierwotnego
. Opcja
kupna daje niezerową wypłatę, gdy cena instrumentu pierwotnego ![]() jest większa niż stała
jest większa niż stała ![]() (cena wykonania), natomiast opcja
sprzedaży daje zysk, gdy
(cena wykonania), natomiast opcja
sprzedaży daje zysk, gdy ![]() .
.
Takie opcje na ogół łatwo wyceniać (patrz ćw. 11.5). Inna spotykana nazwa takich opcji to opcje cyfrowe (digital).
6. Opcje zależne od trajektorii (path-dependent
options). Są to opcje, dla których funkcja wypłaty zależy od cen
akcji w całym okresie trwania kontraktu, tj. ![]() , gdzie
, gdzie ![]() jest funkcją rzeczywistą określona na przestrzeni funkcji ciągłych
jest funkcją rzeczywistą określona na przestrzeni funkcji ciągłych
![]() (dla ustalonej
(dla ustalonej ![]() trajektoria procesu cen
trajektoria procesu cen
![]() należy do przestrzeni
należy do przestrzeni ![]() ).
).
a) Przykład takich opcji stanowią opcje azjatyckie, dla których
wypłata zależy od średniej ceny waloru w określonym przedziale
czasowym ![]() . Są one bardzo popularne na rynku, gdyż są
tańsze do odpowiadających im standardowych opcji europejskich, są
użyteczne na rynkach o małej płynności, a więc na rynkach o większym
ryzyku, a ponadto branie średniej zabezpiecza przed manipulacją
cenami blisko daty wygaśnięcia opcji. Wypłatą z opcji kupna jest
. Są one bardzo popularne na rynku, gdyż są
tańsze do odpowiadających im standardowych opcji europejskich, są
użyteczne na rynkach o małej płynności, a więc na rynkach o większym
ryzyku, a ponadto branie średniej zabezpiecza przed manipulacją
cenami blisko daty wygaśnięcia opcji. Wypłatą z opcji kupna jest
![]() , a z opcji sprzedaży
, a z opcji sprzedaży ![]() ,
gdzie
,
gdzie ![]() jest ceną realizacji opcji, a
jest ceną realizacji opcji, a ![]() średnią cena
waloru. Są różne sposoby obliczania średniej
średnią cena
waloru. Są różne sposoby obliczania średniej ![]() np. dla
kontraktu zawartego na
np. dla
kontraktu zawartego na ![]() dni można wziąć
dni można wziąć ![]() jako średnią
arytmetyczną z cen zamknięcia w
jako średnią
arytmetyczną z cen zamknięcia w ![]() -tym dniu
-tym dniu ![]() , czyli
, czyli
![]() , gdzie
, gdzie ![]() to
liczba dni handlu w roku (zwykle przyjmuje się
to
liczba dni handlu w roku (zwykle przyjmuje się ![]() równe 252), ale
też można wziąć jako
równe 252), ale
też można wziąć jako ![]() średnią geometryczną. Rozważa się też
opcje ze średnimi ,,ciągłymi”:
średnią geometryczną. Rozważa się też
opcje ze średnimi ,,ciągłymi”:
— średnią arytmetyczną ![]() ,
,
— średnią geometryczną ![]()
(te średnie otrzymujemy przez przejście graniczne dla średnich
liczonych w sposób dyskretny). Opcje opisane powyżej są to opcje
azjatyckie I rodzaju (average value Asian option). Rozważa się
też opcje azjatyckie II rodzaju (average strike Asian option)
— są to opcje o wypłatach ![]() (dla opcji
kupna) i
(dla opcji
kupna) i ![]() (dla opcji sprzedaży).
(dla opcji sprzedaży).
b) Innym przykładem opcji zależnych od trajektorii są opcje typu lookback (lookback option).
Są to opcje, z których dochód zależy od maksimum lub minimum ceny
instrumentu podstawowego. Właściciel opcji kupna typu lookback ma
zagwarantowane kupno waloru (akcji) po najniższej cenie, po jakiej
walor był sprzedawany w okresie ważności opcji, natomiast właściciel
opcji sprzedaży sprzedaje walor po najwyższej cenie w okresie
![]() . Zatem wypłata z opcji kupna wynosi
. Zatem wypłata z opcji kupna wynosi ![]() ,
a wypłata z opcji sprzedaży to
,
a wypłata z opcji sprzedaży to ![]() , gdzie
, gdzie ![]() ,
,
![]() są, odpowiednio, najmniejszą i największą ceną
instrumentu pierwotnego w ustalonym okresie
są, odpowiednio, najmniejszą i największą ceną
instrumentu pierwotnego w ustalonym okresie ![]() .
.
7. Opcje barierowe (barrier options). Te opcje są też zależne od trajektorii. Wypłata z tych opcji zależy od tego, czy w ustalonym okresie czasu cena waloru spadnie poniżej pewnej ustalonej wartości, lub/oraz czy cena waloru przekroczy pewną ustaloną wartość. Te ustalone wartości nazywa się barierami. Zasadniczo dzielimy je na opcje wyjścia (knock-out option) i wejścia (knock-in option). Opcje wyjścia przestają istnieć, gdy cena waloru przekroczy pewną ustaloną barierę, a opcje wejścia zaczynają istnieć, gdy cena waloru przekroczy barierę.
Standardowo wypłata z opcji barierowych jest wypłatą z opcji waniliowych, gdy zostanie spełniony warunek związany z barierą. Standardowo dla opcji kupna występują następujące rodzaje opcji:
-
Opcje, które zostają unieważnione, gdy zachodzi jeden z przypadków:
-
cena waloru spadnie poniżej bariery
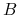 (opcja down-and-out),
wtedy wypłata dla opcji kupna wynosi:
(opcja down-and-out),
wtedy wypłata dla opcji kupna wynosi: 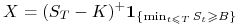 ,
, -
cena waloru przekroczy barierę
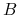 (opcja up-and-out), wtedy
wypłata dla opcji kupna wynosi:
(opcja up-and-out), wtedy
wypłata dla opcji kupna wynosi: 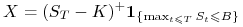 .
.
-
-
Opcje, które uzyskują ważność, gdy zachodzi jeden z przypadków:
-
cena waloru przekroczy barierę
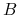 (opcja up-and-in), wtedy
wypłata dla opcji kupna wynosi:
(opcja up-and-in), wtedy
wypłata dla opcji kupna wynosi: 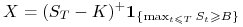 ,
, -
cena waloru spadnie poniżej bariery
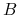 (opcja down-and-in), wtedy
wypłata dla opcji kupna wynosi:
(opcja down-and-in), wtedy
wypłata dla opcji kupna wynosi: 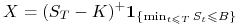 .
.
-
Warto zauważyć, że suma wypłat z opcji typu up, jak i typu out są równe wypłacie ze standardowej opcji kupna.
Analogicznie określone są standardowe opcje barierowe związane z opcją sprzedaży.
Istnieje też wiele innych opcji tego typu (tzw. opcje kombinowane) np. opcja o wypłacie
8. Opcje z nieliniową wypłatą. Są to opcje, których wypłata
jest nieliniową funkcją ceny instrumentu pierwotnego ![]() w momencie wykonania opcji
w momencie wykonania opcji ![]() , zatem opcje kupna są to opcje
o wypłacie
, zatem opcje kupna są to opcje
o wypłacie ![]() , gdzie
, gdzie ![]() jest dowolną nieliniową
funkcją np. opcja potęgowa z parametrem
jest dowolną nieliniową
funkcją np. opcja potęgowa z parametrem ![]() jest to opcja dla
której
jest to opcja dla
której ![]() ,
, ![]() ,
, ![]() .
.
Istnieje wiele innych opcji egzotycznych, m.in. złożone, kwantylowe, koszykowe. Więcej na ten temat można znaleźć np. w książkach Kwoka [Kwok] oraz A. Werona i R. Werona [Wer].
Jak już wspominaliśmy, wycena opcji egzotycznych jest na ogół
trudnym zadaniem i bardzo często otrzymuje się formuły niejawne.
Czasem można znaleźć wzór analityczny, np. dla opcji potęgowej
z parametrem ![]() otrzymujemy
otrzymujemy
gdzie ![]() (patrz ćw. 11.3).
(patrz ćw. 11.3).
Nie potrafimy już jednak znaleźć jawnych wzorów na cenę opcji
nieliniowej o bardziej skomplikowanej postaci funkcji ![]() . W takich
przypadkach często stosuje się metody symulacyjne opierające się na
mocnym prawie wielkich liczb. Zwykle takie wypłaty wycenia się za
pomocą symulacji komputerowych i procedur numerycznych bazujących na
przybliżaniu geometrycznego ruchu Browna przez model CRR.
. W takich
przypadkach często stosuje się metody symulacyjne opierające się na
mocnym prawie wielkich liczb. Zwykle takie wypłaty wycenia się za
pomocą symulacji komputerowych i procedur numerycznych bazujących na
przybliżaniu geometrycznego ruchu Browna przez model CRR.
Jak wiemy, osiągalna wypłata ![]() w chwili
w chwili ![]() ma w chwili 0 cenę
ma w chwili 0 cenę ![]() . Zatem, aby znaleźć cenę wypłaty
. Zatem, aby znaleźć cenę wypłaty ![]() ,
należy obliczyć wartość oczekiwaną
,
należy obliczyć wartość oczekiwaną ![]() przy mierze
martyngałowej
przy mierze
martyngałowej ![]() . Do wyliczenia tej wartości oczekiwanej używamy
metod Monte Carlo. Symulujemy przebieg trajektorii procesu ceny
instrumentu bazowego
. Do wyliczenia tej wartości oczekiwanej używamy
metod Monte Carlo. Symulujemy przebieg trajektorii procesu ceny
instrumentu bazowego ![]() w skończonej liczbie punktów (korzystamy
z tego, że przy mierze martyngałowej
w skończonej liczbie punktów (korzystamy
z tego, że przy mierze martyngałowej ![]() ceny
ceny ![]() mają rozkład
normalny (wzór (9.16)), który znamy, gdy znamy
mają rozkład
normalny (wzór (9.16)), który znamy, gdy znamy ![]() i
i ![]() ). Następnie obliczamy wartość wypłaty
). Następnie obliczamy wartość wypłaty ![]() przy tej
realizacji trajektorii i otrzymujemy liczbę
przy tej
realizacji trajektorii i otrzymujemy liczbę ![]() . Powtarzamy to
postępowanie niezależnie
. Powtarzamy to
postępowanie niezależnie ![]() razy i otrzymujemy z tej symulacji ciąg
wypłat
razy i otrzymujemy z tej symulacji ciąg
wypłat ![]() . Korzystając z mocnego prawa wielkich
liczb otrzymujemy, że cena wypłaty wynosi w przybliżeniu
. Korzystając z mocnego prawa wielkich
liczb otrzymujemy, że cena wypłaty wynosi w przybliżeniu
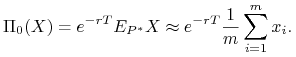 |
Przykład 11.2
Prześledzimy to rozumowanie na przykładzie opcji lookback
Zaczynamy od wyznaczenia trajektorii ceny akcji. Termin do wykonania
opcji dzielimy na ![]() równych odcinków czasu. Niech
równych odcinków czasu. Niech ![]() będzie
ceną na końcu i-tego odcinka,
będzie
ceną na końcu i-tego odcinka, ![]() ,
, ![]() . Wtedy, jak
wiemy z (9.16)
. Wtedy, jak
wiemy z (9.16)
gdzie ![]() ma rozkład normalny
ma rozkład normalny
przy czym ![]() jest długością odcinka czasu liczoną w skali roku,
jest długością odcinka czasu liczoną w skali roku,
![]() . Ponadto
. Ponadto ![]() są niezależnymi zmiennymi
losowymi. Stąd
są niezależnymi zmiennymi
losowymi. Stąd
| (11.7) |
Za pomocą tego przedstawienia wyliczamy trajektorie cen. Najpierw
generujemy wyniki ![]() niezależnych zmiennych losowych o rozkładzie
niezależnych zmiennych losowych o rozkładzie
![]() i otrzymujemy ciąg realizacji
i otrzymujemy ciąg realizacji ![]() . Następnie
wyliczamy ceny na końcu każdego odcinka czasu korzystając
z (11.7):
. Następnie
wyliczamy ceny na końcu każdego odcinka czasu korzystając
z (11.7):
Dla tej konkretnej realizacji cen obliczamy zdyskontowaną wartość opcji lookback:
Powtarzamy tę procedurę ![]() razy otrzymując ciąg wyników
razy otrzymując ciąg wyników ![]() i bierzemy ich średnią arytmetyczną jako estymator
Monte Carlo ceny opcji.
i bierzemy ich średnią arytmetyczną jako estymator
Monte Carlo ceny opcji.
Klasyczna metoda Monte Carlo jest nieefektywna, więc stosuje się jej ulepszenia, ale idea wyceny pozostaje ta sama. Więcej informacji na ten temat, a także na temat innych metod numerycznych stosowanych w finansach, czytelnik może znaleźć w monografiach Glassermana [Gla], Jäckela [Ja] i Seydela [Sey].
11.3. Zagadnienia i zadania na ćwiczenia
Ćwiczenie 11.1
Udowodnić, że istnieje portfel dopuszczalny ![]() o kapitale
początkowym
o kapitale
początkowym ![]() zabezpieczający wypłatę związaną z opcją
amerykańską, tj.
zabezpieczający wypłatę związaną z opcją
amerykańską, tj. ![]() . Udowodnić, że dla tego
portfela zachodzi równość
. Udowodnić, że dla tego
portfela zachodzi równość
gdzie ![]() jest optymalnym momentem wykonania.
jest optymalnym momentem wykonania.
Z tw. Dooba-Meyera ![]() , gdzie
, gdzie ![]() jest martyngałem,
jest martyngałem, ![]() — procesem rosnącym
prognozowalnym,
— procesem rosnącym
prognozowalnym, ![]() . Z tw. o reprezentacji martyngału
. Z tw. o reprezentacji martyngału
dla pewnego procesu ![]() całkowalnego względem
całkowalnego względem ![]() .
.
Strategia
| (11.8) |
spełnia warunki zadania. Istotnie, z (11.4)
a dla ![]() optymalnego momentu wykonania zachodzi równość.
optymalnego momentu wykonania zachodzi równość.
Ćwiczenie 11.2
Udowodnić, że warunek
implikuje brak arbitrażu na rynku ![]() .
.
Nie wprost. Niech cena opcji amerykańskiej ![]() spełnia
spełnia ![]() (opcja jest na rynku
przewartościowana).
(opcja jest na rynku
przewartościowana).
Skonstruujemy arbitraż związany z pozycją krótką. Weźmy strategię
![]() daną wzorem (11.8) i strategię ,,kup
i trzymaj”
daną wzorem (11.8) i strategię ,,kup
i trzymaj” ![]() , gdzie
, gdzie ![]() jest
dowolnym momentem stopu. Niech strategia
jest
dowolnym momentem stopu. Niech strategia ![]() będzie zadana wzorem:
będzie zadana wzorem:
Ponieważ ![]() spełnia (11.5), więc
spełnia (11.5), więc
a ponadto
Zatem strategia ![]() jest arbitrażem.
jest arbitrażem.
Rozpatrzymy teraz przypadek ![]() (opcja na rynku jest
niedowartościowana).
(opcja na rynku jest
niedowartościowana).
Możemy założyć, że nabywca opcji zachowuje się racjonalnie i wybiera
optymalny moment realizacji opcji. Gdy wybierze on portfel ![]() , to
, to
i z określenia optymalnego momentu realizacji opcji wynika, że
![]() .
.
Ćwiczenie 11.3
Wycenić opcję potęgową
Ćwiczenie 11.4
W modelu Blacka-Scholesa wycenić na chwilę ![]() opcje binarne
płacące:
opcje binarne
płacące:
a) ![]() ,
,
b) ![]() ,
,
c) ![]() ,
,
gdzie ![]() są stałymi.
są stałymi.
Jak wiemy z uwagi 9.2, cena ![]() , gdzie
, gdzie
a stąd a)
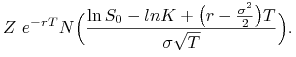 |
b)
gdzie ![]() i
i ![]() . Ostatnią równość
można otrzymać np. metodą zamiany miary, jak w dowodzie tw. Blacka.
. Ostatnią równość
można otrzymać np. metodą zamiany miary, jak w dowodzie tw. Blacka.
Ćwiczenie 11.5
W modelu Blacka-Scholesa wycenić na chwilę ![]() opcje binarne płacące:
opcje binarne płacące:
a) ![]() ,
,
b) ![]() .
.
Wyprowadzić wzór łączący te dwie ceny.
Ćwiczenie 11.6
Znaleźć w chwili ![]() cenę zmodyfikowanej opcji startującej
w przyszłości, czyli opcji o wypłacie
cenę zmodyfikowanej opcji startującej
w przyszłości, czyli opcji o wypłacie ![]() ,
gdzie stała
,
gdzie stała ![]() .
.




