Zagadnienia

3.1 Model rynku, portfel
3.2 Arbitraż
3.3 Wypłata europejska i jej wycena
3.4 Zagadnienia i zadania na ćwiczenia

3. Rynki skończone

Teraz uogólnimy model z poprzedniego wykładu. Dopuścimy dowolną skończoną liczbę możliwych scenariuszy i skończenie wiele chwil czasu, w których dokonuje się transakcji. Taki rynek będziemy nazywać rynkiem skończonym. Ograniczenie liczby możliwych scenariuszy pozwala uniknąć stosowania zaawansowanych narzędzi technicznych i pozwala skupić się na interpretacjach stosowanych metod i otrzymywanych wyników.

3.1. Model rynku, portfel

Założymy, że mamy do czynienia z rynkiem wielookresowym, czyli chwile czasu, w których odbywają się transakcje, to są chwile $0,1,2,\dots,T$ (w zależności od sytuacji odpowiada to minutom, dniom, itp.), gdzie horyzont czasowy jest skończony: $T<\infty$ . Założymy ponadto, że liczba możliwych scenariuszy (przypadków) jest skończona, zatem przestrzeń probabilistyczna

$\Omega=\{\omega _{{1}},\omega _{{2}},\dots,\omega _{{d}}\}$

jest zbiorem skończonym, rodzina zdarzeń ${\cal F}=2^{{\Omega}}$ , a prawdopodobieństwo $P$ jest takie, że

$P(\{\omega _{{i}}\})>0,\quad i=1,2,\dots,d.$

Wprowadźmy $\sigma$ -ciała ${\cal F}_{t}$ , $t\in\{ 0,1,\dots,T\}$ , które interpretujemy jako zasób wiedzy o rynku zebrany do chwili $t$ . Nasza wiedza z czasem rośnie: ${\cal F}_{t}\subset{\cal F}_{s}$ dla $t\leq s$ , więc ciąg ${\cal F}_{{t}}$ jest filtracją. Bez straty ogólności możemy założyć, że ${\cal F}_{0}$ jest $\sigma$ -ciałem trywialnym i ${\cal F}_{{T}}={\cal F}$ . Dla wygody oznaczmy

${\cal T}=\{ 0,1,\dots,T\}.$

Na rynku znajduje się $(k+1)$ instrumentów finansowych (instrumenty pierwotne), których ceny za jedną jednostkę w chwili $t$ są opisywane przez zmienne losowe $S_{{t}}^{{0}},S_{{t}}^{{1}},\dots,S_{{t}}^{{k}}$ . Są one ${\cal F}_{t}$ -mierzalne, gdyż nasza dzisiejsza wiedza nie pozwala nam przewidzieć przyszłych cen: w chwili $t$ znamy jedynie ceny $S_{{u}}^{{i}}$ dla $u\leq t$ . Zatem wektor cen

$S_{t}=(S_{{t}}^{{0}},S_{{t}}^{{1}},\dots,S_{{t}}^{{k}})^{{\prime}},$

gdzie symbol ${}^{{\prime}}$ oznacza transpozycję, jest ciągiem adaptowanych zmiennych losowych. $S_{0}$ jest wektorem cen początkowych, które znamy (cen w chwili zero), więc jest to wektor stały o wartościach w $\mathbb{R}^{{k+1}}$ . Zwykle przyjmuje się (i to robimy), że $S^{{0}}$ jest ceną aktywa bezryzykownego. Zakładamy, że $S_{0}^{{0}}=1$ i kapitalizacja jest okresowa, oprocentowanie jest stałe i równe w skali jednego okresu $r$ , $r\geq 0$ , a więc

$S_{{t}}^{{0}}=(1+r)^{{t}}.$

(3.1)

Zatem $\beta _{{t}}=1/{S_{{t}}^{{0}}}$ jest czynnikiem dyskontującym, czyli gdy zainwestujemy $\beta _{{t}}$ w chwili $0$ , to otrzymamy $1$ w chwili $t$ . Rynek spełniający powyższe założenia będziemy nazywać rynkiem skończonym.

Strategią finansową (portfelem, procesem portfelowym) będziemy nazywać dowolny proces prognozowalny $(\varphi _{{t}})_{{t\in{\cal T}}}$ o wartościach w $\mathbb{R}^{{k+1}}$ :

$\varphi _{{t}}=(\varphi _{{t}}^{{0}},\varphi _{{t}}^{{1}},\dots,\varphi _{{t}}^{{k}})^{{\prime}},$

czyli $\varphi _{0}^{{i}}$ jest zmienną losową ${\cal F}_{0}$ -mierzalną, a dla $t=1,2,\dots,T$ zmienna losowa $\varphi _{{t}}^{{i}}$ jest ${\cal F}_{{t-1}}$ -mierzalna. Zmienną losową $\varphi _{{t}}^{{i}}$ , czyli $i$ -tą współrzędną wektora $\varphi _{{t}}$ interpretujemy jako liczbę jednostek $i$ -tego waloru trzymanych w portfelu od chwili $t-1$ do chwili $t$ . Wielkości $\varphi _{{t}}^{{i}}$ są dowolnymi liczbami rzeczywistymi, co odzwierciedla fakt, że dopuszczamy krótką sprzedaż, możliwość zaciągania kredytu w dowolnej wysokości i zakładamy nieskończoną podzielność papierów. Prognozowalność $\varphi$ jest matematycznym sformułowaniem faktu, że portfel na chwilę $t$ , czyli wektor $\varphi _{{t}}$ jest konstruowany na podstawie wiedzy osiągalnej do chwili $t-1$ (tj. wiedzy sprzed momentu $t$ ) i nie zmienia się do chwili $t$ , w której inwestor poznaje nowe ceny. Wtedy inwestor konstruuje nowy skład portfela na następną chwilę $(t+1)$ , czyli $\varphi _{{t+1}}$ .

Definicja 3.1

Wartością portfela $\varphi$ $($ procesem wartości, bogactwem $)$ w chwili $t$ nazywamy zmienną losową:

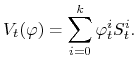$V_{{t}}(\varphi)=\sum _{{i=0}}^{{k}}\varphi _{{t}}^{{i}}S_{{t}}^{{i}}.$

Ponieważ $V_{t}(\varphi)$ jest iloczynem skalarnym wektorów losowych $\varphi _{{t}}$ i $S_{{t}}$ , to będziemy używać notacji iloczynowej: $V_{{t}}(\varphi)=\varphi _{{t}}S_{{t}}.$ Wielkość $V_{0}(\varphi)=\varphi _{0}S_{0}$ jest nazywana kapitałem początkowym lub wielkością początkową inwestycji.

Niektórzy autorzy przez portfel rozumieją parę $(x,\varphi)$ , gdzie $x$ jest kapitałem początkowym, a proces prognozowalny $\varphi=(\varphi _{{t}})_{{t\in\{{1,...,T}\}}}$ jest strategią postępowania w kolejnych chwilach czasu. To podejście jest równoważne prezentowanemu na wykładzie, gdyż $x$ jest jednoznacznie wyznaczony przez $\varphi _{0}$ , a mianowicie $x=\varphi _{0}S_{0}$ .

Gdy inwestor w chwili $t$ konstruuje portfel $\varphi _{{t+1}}$ na chwilę $(t+1)$ , to koszt konstrukcji tego portfela wynosi $\varphi _{{t+1}}S_{{t}}$ , a jego wartość w chwili na którą był on konstruowany, a więc w chwili $(t+1)$ wynosi $\varphi _{{t+1}}S_{{t+1}}$ (opisujemy rynek doskonały, a więc bez kosztów transakcji, podatków itp.). Czyli wielkość $\varphi _{{t+1}}S_{{t+1}}-\varphi _{{t+1}}S_{{t}}$ jest zyskiem w chwili $t+1$ wynikającym ze zmiany cen. Stąd

Definicja 3.2

Proces zysku $G(\varphi)$ portfela $\varphi$ definiowany jest wzorem

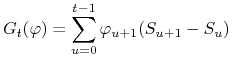$G_{{t}}(\varphi)=\sum _{{u=0}}^{{t-1}}\varphi _{{u+1}}(S_{{u+1}}-S_{{u}})$

(3.2)

dla $t=1,\dots,T$ .

Wyróżnimy teraz specjalną klasę portfeli:

Definicja 3.3

Strategię nazywamy samofinansującą się, gdy

$\varphi _{{t}}S_{{t}}=\varphi _{{t+1}}S_{{t}}$

(3.3)

dla $t=0,1,\dots,T-1$ .

Ta własność strategii oznacza, że inwestor zmienia swoją pozycję (portfel) z $\varphi _{{t}}$ na $\varphi _{{t+1}}$ bez konsumpcji lub dopływu kapitału z zewnątrz. W chwili $t$ inwestor dysponuje kapitałem $V_{{t}}(\varphi)$ , który w całości przeznacza na zakup portfela $\varphi _{{t+1}}$ , płacąc ceny $S_{{t}}$ za aktywa.

Niech $\Phi$ będzie klasą strategii samofinansujących się. Wprost z definicji wynika, że $\Phi$ jest przestrzenią liniową. Podamy teraz bardzo przydatną charakteryzację portfeli samofinansujących się, mówiącą, że w chwili $t$ kapitał takiego portfela jest równy sumie kapitału początkowego i wartości procesu zysku tego portfela w tej chwili. Zysk w chwili $t$ jest sumą zysków w poprzednich chwilach wynikających tylko ze zmiany cen z $S_{{u}}$ w chwili $u$ na $S_{{u+1}}$ w chwili $u+1$ , gdzie $u=0,\ldots,T-1$ .

Twierdzenie 3.1

Portfel $\varphi$ jest samofinansujący się wtedy i tylko wtedy, gdy dla wszystkich $t$ spełniona jest równość

$V_{{t}}(\varphi)=V_{0}(\varphi)+G_{{t}}(\varphi).$

(3.4)

Konieczność.

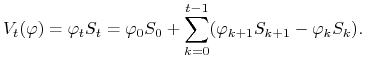$V_{{t}}(\varphi)=\varphi _{{t}}S_{{t}}=\varphi _{0}S_{0}+\sum _{{k=0}}^{{t-1}}(\varphi _{{k+1}}S_{{k+1}}-\varphi _{{k}}S_{{k}}).$

Korzystając z założenia $\varphi _{{u}}S_{{u}}=\varphi _{{u+1}}S_{{u}}$ , mamy

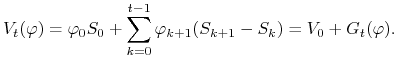$V_{{t}}(\varphi)=\varphi _{0}S_{0}+\sum _{{k=0}}^{{t-1}}\varphi _{{k+1}}(S_{{k+1}}-S_{{k}})=V_{0}+G_{{t}}(\varphi).$

Dostateczność. Z założenia (3.4) dla dowolnego $t$ mamy

$V_{{t+1}}(\varphi)-V_{{t}}(\varphi)=\varphi _{{t+1}}(S_{{t+1}}-S_{{t}}).$

(3.5)

Ponadto, z definicji

$V_{{t+1}}(\varphi)-V_{{t}}(\varphi)=\varphi _{{t+1}}S_{{t+1}}-\varphi _{{t}}S_{{t}}.$

Porównując prawe strony widzimy, że $\varphi _{{t}}S_{{t}}=\varphi _{{t+1}}S_{{t}}$ dla wszystkich $t$ , co oznacza, że $\varphi\in\Phi$ .

∎

Z powyższego twierdzenia wynika, że bogactwo portfela dla strategii samofinansującej się zależy tylko od portfela i zmian cen.

Uwaga 3.1

Z dowodu tw. 3.1 wynika, że portfel $\varphi$ jest samofinansujący się wtedy i tylko wtedy, gdy dla wszystkich $t$ zachodzi (3.5), czyli:

$\varphi\in\Phi\quad\Longleftrightarrow\quad V_{{t+1}}(\varphi)-V_{{t}}(\varphi)=\varphi _{{t+1}}(S_{{t+1}}-S_{{t}})\quad\hbox{dla każdego $t$}.$

Ćwiczenie 3.1

Udowodnić, że portfel stały jest strategią samofinansującą się.

Rozwiązanie:

Ponieważ iloczyn skalarny jest liniowy, więc

$\varphi\in\Phi\quad\Longleftrightarrow\quad(\varphi _{{t+1}}-\varphi _{{t}})S_{{t}}=0\quad\hbox{dla każdego $t$},$

(3.6)

a stąd teza wynika natychmiast.

Okazuje się, że gdy inwestor postępuje zgodnie ze strategią samofinansującą, to wartość portfela jest całkowicie zdeterminowana przez bogactwo początkowe i strategię postępowania z aktywami ryzykownymi.

Twierdzenie 3.2

Dla dowolnego procesu prognozowalnego $(\varphi _{{t}}^{{1}},\dots,\varphi _{{t}}^{{k}})^{{\prime}}$ , $t={\in}\{ 0,1,\dots,T\}$ i dowolnego rzeczywistego $x$ istnieje jednoznacznie wyznaczony proces prognozowalny $\varphi _{{t}}^{{0}}$ , $t\in\{ 0,1,\dots,T\}$ , taki, że strategia $\varphi=(\varphi^{{0}},\dots,\varphi^{{k}})^{{\prime}}$ jest samofinansującą się i jej początkowe bogactwo jest równe $x$ .

Wielkość początkowa inwestycji jest równa $x$ , zatem

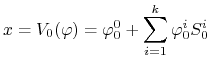$x=V_{0}(\varphi)=\varphi _{0}^{{0}}+\sum _{{i=1}}^{{k}}\varphi _{0}^{{i}}S_{0}^{{i}}$

i stąd mamy wyznaczoną jednoznacznie stałą $\varphi _{0}^{{0}}$ :

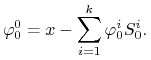$\varphi _{0}^{{0}}=x-\sum _{{i=1}}^{{k}}\varphi _{0}^{{i}}S_{0}^{{i}}.$

Dalej skorzystamy z zasady indukcji matematycznej. Załóżmy, że $\varphi _{{t}}$ jest wyznaczone jednoznacznie i jest ${\cal F}_{{t-1}}$ -mierzalne. Z warunku samofinansowalności (3.3) mamy

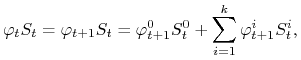$\varphi _{{t}}S_{{t}}=\varphi _{{t+1}}S_{{t}}=\varphi _{{t+1}}^{{0}}S_{{t}}^{{0}}+\sum _{{i=1}}^{{k}}\varphi _{{t+1}}^{{i}}S_{{t}}^{{i}},$

a stąd $\varphi _{{t+1}}^{{0}}$ jest wyznaczone jednoznacznie wzorem

$\varphi _{{t+1}}^{{0}}=\frac{1}{S_{{t}}^{{0}}}\Big[\varphi _{{t}}S_{{t}}-\sum _{{i=1}}^{{k}}\varphi _{{t+1}}^{{i}}S_{{t}}^{{i}}\Big].$

Wszystkie składniki z prawej strony są ${\cal F}_{{t}}$ -mierzalne, więc $\varphi _{{t+1}}^{0}$ jest ${\cal F}_{{t}}$ –mierzalne. Mamy zatem jednoznacznie określony proces prognozowalny $(\varphi _{{t}}^{{0}})_{{t}}$ .

∎

3.2. Arbitraż

Definicja 3.4

Strategię $\varphi$ nazywamy arbitrażem $($ strategią arbitrażową $)$ , gdy

$V_{0}(\varphi)=0$

oraz

$P(V_{{T}}(\varphi)\geq 0)=1,\quad P(V_{{T}}(\varphi)>0)>0.$

Uwaga 3.2

Ponieważ $P(\{\omega _{{i}}\})>0$ dla każdego $i$ , więc warunki z definicji są równoważne następującym:

$\forall _{{\omega\in\Omega}}\ \mbox{ zachodzi }\ V_{0}(\varphi)(\omega)=0,\ V_{{T}}(\varphi)(\omega)\geq 0$

oraz

$\exists _{{\omega _{{i}}}}\mbox{ takie, że }V_{{T}}(\varphi)(\omega _{{i}})>0.$

b) Warunek braku arbitrażu na rynku można też wyrazić inaczej:

$\forall\varphi\in\Phi\quad V_{0}(\varphi)=0,\quad V_{{T}}(\varphi)\geq 0\quad P-p.n.\quad\Rightarrow\quad V_{{T}}(\varphi)=0.$

Widać, że definicja 3.4 uogólnia pojęcie arbitrażu dla rynku jednookresowego dwustanowego, a jednocześnie wyraża to pojęcie w terminach prawdopodobieństwa i nie używa pojęcia scenariusza, więc łatwo ją przenieść na szerszą klasę modeli.

Definicja 3.5

Modelem rynku finansowego nazwiemy pare ${\cal M}=(S,\Phi)$ . Rynek nazywamy rynkiem bez możliwości arbitrażu $($ bezarbitrażowym, pozbawionym arbitrażu $)$ , gdy nie istnieje strategia arbitrażowa w klasie strategii samofinansujących się.

Pojęcie arbitrażu zdefiniowaliśmy globalnie. Okazuje się, że nasza definicja obejmuje przypadek, gdy można mieć zysk bez żadnego nakładu i bez ryzyka we wcześniejszych chwilach czasu. Intuicyjnie można to uzasadnić w następujący sposób: wiemy, że istnieje arbitraż w chwili $t<T$ na pewnym zbiorze $A$ . Wtedy wybieramy strategię wstrzymania się od jakichkolwiek działań do momentu $t$ . Gdy w chwili $t$ znajdziemy się w zbiorze $A$ (zatem scenariusz sprzyjał zajściu zdarzenia $A$ ), to wykorzystujemy naszą okazję. Wchodzimy w kontrakt arbitrażowy, następnie w chwili $(t+1)$ realizujemy zysk, który natychmiast wkładamy na rachunek bankowy i ostatecznie osiągamy dodatni zysk. Gdy w chwili $t$ nie znajdziemy się w zbiorze $A$ , to nic nie robimy (zatem na końcu mamy zero). Tę intuicję potwierdza twierdzenie mówiące, że jeśli na rynku nie istnieje arbitraż globalny, to nie istnieje arbitraż lokalny, czyli arbitraż w jednym okresie. Aby móc porównywać wartość portfela w różnych chwilach czasu musimy uwzględniać oprocentowanie, zatem porównujemy zdyskontowane wartości portfela, czyli porównujemy w różnych chwilach wartości procesu $V^{*}_{t}(\varphi)=V_{t}(\varphi)/S^{0}_{t}$ . Dlatego twierdzenie o arbitrażu lokalnym przybiera postać:

Twierdzenie 3.3

Jeżeli na rynku $(S,\Phi)$ nie ma możliwości arbitrażu, to dla każdego $t\in\{ 0,\dots,T-1\}$ , $A\in{\cal F}_{{t}}$ i dla $\varphi\in\Phi$ mamy

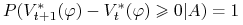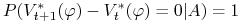i) $P(V^{*}_{{t+1}}(\varphi)-V^{*}_{{t}}(\varphi)\geq 0|A)=1$ implikuje $P(V^{*}_{{t+1}}(\varphi)-V^{*}_{{t}}(\varphi)=0|A)=1$ .
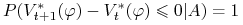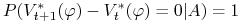ii) $P(V^{*}_{{t+1}}(\varphi)-V^{*}_{{t}}(\varphi)\leq 0|A)=1$ implikuje $P(V^{*}_{{t+1}}(\varphi)-V^{*}_{{t}}(\varphi)=0|A)=1$ .

Sformalizujemy idee opisane powyżej. Udowodnimy punkt i) twierdzenia. Ustalmy chwilę $t$ , strategię $\varphi\in\Phi$ i $A\in{\cal F}_{t}$ takie, że $P(A)>0$ i

$P(V^{*}_{{t+1}}(\varphi)-V^{*}_{t}(\varphi)\geq 0|A)=1.$

(3.7)

Zdefiniujemy teraz proces $\psi$ . Niech $\psi _{0}=0$ , a dla $0<u~\leq T$ niech

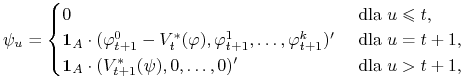$\psi _{u}=\begin{cases}0&\text{ dla }u\leq t,\cr{\bf 1}_{A}\cdot(\varphi^{0}_{{t+1}}-V^{*}_{t}(\varphi),\varphi^{1}_{{t+1}},\dots,\varphi^{k}_{{t+1}})^{{\prime}}&\text{ dla }u=t+1,\cr{\bf 1}_{A}\cdot(V^{*}_{{t+1}}(\psi),0,\dots,0)^{{\prime}}&\text{ dla }u>t+1,\end{cases}$

gdzie ${\bf 1}_{A}$ jest funkcją wskaźnikową zbioru $A$ , tj.

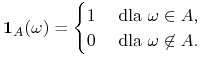${\bf 1}_{A}(\omega)=\begin{cases}1&\text{ dla }\omega\in A,\cr 0&\text{ dla }\omega\not\in A.\end{cases}$

Z postaci $\psi$ wynika, że jest to proces prognozowalny, a więc $\psi$ jest portfelem. Sprawdzamy teraz, że portfel $\psi$ jest samofinansujący się, korzystając z warunku (3.6) i z tego, że $\varphi\in\Phi$ .

Gdy $u<t$ lub $u>t+1$ , to $\psi _{{u+1}}-\psi _{u}=0$ , więc $(\psi _{{u+1}}-\psi _{u})S_{u}=0$ .

Gdy $u=t$ , to

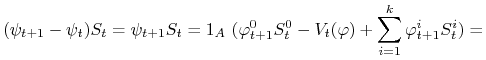	$\displaystyle(\psi _{{t+1}}-\psi _{{t}})S_{t}=\psi _{{t+1}}S_{t}=1_{A}\ (\varphi _{{t+1}}^{0}S^{0}_{t}-V_{t}(\varphi)+\sum _{{i=1}}^{k}\varphi _{{t+1}}^{i}S_{t}^{i})=$
	$\displaystyle={\bf 1}_{A}\ (\varphi _{{t+1}}S_{t}-V_{t}(\varphi))={\bf 1}_{A}\ (\varphi _{t}S_{t}-V_{t}(\varphi))=0.$

Natomiast gdy $u=t+1$ , to

$(\psi _{{t+2}}-\psi _{{t+1}})S_{{t+1}}={\bf 1}_{A}\ (V^{*}_{{t+1}}(\psi)S_{{t+1}}^{0}-V_{{t+1}}(\psi))=0.$

Ponieważ $V^{*}_{{t+1}}(\psi)={\bf 1}_{A}(V^{*}_{{t+1}}(\varphi)-V^{*}_{t}(\varphi))$ , więc z (3.7) i definicji $\psi _{T}$ otrzymujemy

$V_{T}(\psi)=\psi _{T}S_{T}={\bf 1}_{A}\cdot(V^{*}_{{t+1}}(\varphi)-V^{*}_{t}(\varphi))\, S^{0}_{T}\geq 0.$

Stąd, oraz z tego, że $\psi\in\Phi$ , $V_{0}(\psi)=0$ oraz z założenia o braku arbitrażu wynika, że $V_{T}(\psi)=0$ . Zatem

	$\displaystyle 0$	$\displaystyle=$	$\displaystyle P(V_{T}(\psi)>0)=P(\{ V_{T}(\psi)>0\}\cap A)=$
		$\displaystyle=$	$\displaystyle P(V^{}_{{t+1}}(\varphi)-V^{}_{t}(\varphi)>0\|A)\cdot P(A).$

Ponieważ $P(A)>0$ , więc $P(V^{*}_{{t+1}}(\varphi)-V^{*}_{t}(\varphi)>0|A)=0$ , zatem

$P(V^{*}_{{t+1}}(\varphi)-V^{*}_{{t}}(\varphi)=0|A)=1,$

co wraz z założeniem (3.7) daje punkt i).

Punkt ii) dowodzi się analogicznie.

∎

3.3. Wypłata europejska i jej wycena

Teraz naszym celem będzie podanie metody wyceny i zabezpieczania instrumentów finansowych na rynku bez możliwości arbitrażu. Jak zawsze, instrument europejski utożsamiamy z wypłatą, którą otrzymuje jego posiadacz w określonej chwili $T$ , wobec tego zaczniemy od ścisłej definicji wypłaty.

Definicja 3.6

Wypłatą $($ europejską $)$ $X$ w chwili $T$ nazywamy dowolną ${\cal F}_{T}$ –mierzalną zmienną losową.

Oznacza to, że wypłata europejska zależy od wiedzy zebranej na rynku. Gdy wypłata zależy od cen instrumentów podstawowych tzn. od $S$ , to instrument nazywamy instrumentem pochodnym. Później zajmiemy się instrumentami, których nie da się opisać przy pomocy jednej wypłaty w momencie $T$ .

Strategię $\varphi\in\Phi$ nazywamy strategią replikującą wypłatę $X$ gdy

$V_{{T}}(\varphi)=X,$

czyli gdy wartość portfela w chwili $T$ jest równa $X$ . Wypłatę $X$ nazywa się osiągalną, gdy istnieje strategia ją replikująca. Warto zauważyć, że wypłaty osiągalne tworzą podprzestrzeń liniową w zbiorze wypłat.

Mówimy, że wypłata jest jednoznacznie replikowalna w modelu ${\cal M}$ , gdy dla dowolnych strategii $\varphi,\psi$ replikujących $X$ mamy $V_{{t}}(\varphi)=V_{{t}}(\psi)$ dla wszystkich $t$ . Wtedy proces $V_{{t}}(\varphi)$ nazywamy procesem replikującym $X$ lub procesem bogactwa $X$ w ${\cal M}$ . Jak wiemy, na rynku jednookresowym dwustanowym wszystkie wypłaty są osiągalne, istnieje dokładnie jedna strategia replikująca, więc wypłaty osiągalne są jednoznacznie replikowalne. W modelu rynku skończonego nie wszystkie wypłaty są osiągalne (patrz ćw. 3.10), ale wypłaty osiągalne są jednoznacznie replikowalne, choć nie oznacza to, że istnieje dokładnie jedna strategia replikująca (patrz zad. 3.9).

Twierdzenie 3.4

Jeśli ${\cal M}$ jest rynkiem bez możliwości arbitrażu, to każda wypłata $X$ osiągalna w ${\cal M}$ jest jednoznacznie replikowalna w ${\cal M}$ .

Nie wprost. Załóżmy, że istnieją strategie $\varphi$ , $\psi$ replikujące $X$ , takie że dla pewnego $t<T$ mamy $V_{{u}}(\varphi)=V_{{u}}(\psi)$ dla $u<t$ i $V_{{t}}(\varphi)\neq V_{{t}}(\psi)$ . Rozważymy dwa przypadki.

I. Niech $t>0$ i niech $A=\{ V_{{t}}(\varphi)>V_{{t}}(\psi)\}.$ Bez straty ogólności można założyć, że $P(A)>0$ .

Niech $\zeta=V_{{t}}(\varphi)-V_{{t}}(\psi)$ . Z definicji zmiennej losowej $\zeta$ wynika, że przyjmuje ona wartości dodatnie na zbiorze $A$ . Udowodnimy, że strategia $\eta$ zdefiniowana wzorami:

$\eta _{{u}}=\left\{\begin{array}[]{ll}\varphi _{{u}}-\psi _{{u}}&\mbox{ dla }u~\leq t,\\ {\bf 1}_{{A^{c}}}(\varphi _{{u}}-\psi _{{u}})+{\bf 1}_{{A}}(\frac{\zeta}{S_{{t}}^{{0}}},0,\ldots,0)^{{\prime}}&\mbox{ dla }u>t\end{array}\right.$

jest strategią arbitrażową, a więc doprowadzimy do sprzeczności. Strategia $\eta$ jest do chwili $t$ równa różnicy strategii $\varphi$ i $\psi$ . Gdy w chwili $t$ zrealizuje się zdarzenie $A^{c}$ , to nie zmieniamy postępowania, a gdy zrealizuje się zdarzenie $A$ to realizujemy nasz zysk i od chwili $t+1$ trzymamy wszystko w banku. Zaczniemy od wykazania, że strategia $\eta$ jest samofinansująca się. Gdy $u<t$ , to

$\eta _{{u}}S_{{u}}=(\varphi _{{u}}-\psi _{{u}})S_{{u}}=(\varphi _{{u+1}}-\psi _{{u+1}})S_{{u}}=\eta _{{u+1}}S_{{u}},$

przy czym w drugiej równości korzystamy z faktu, że $\varphi$ i $\psi$ są strategiami samofinansującymi się. Dla $u=t$ mamy:

$\eta _{{t}}S_{{t}}=\varphi _{{t}}S_{{t}}-\psi _{{t}}S_{{t}}=V_{t}({\varphi})-V_{{t}}(\psi).$

A ponieważ strategie $\varphi,\psi$ replikujące $X$ są samofinansujące się, więc

	$\displaystyle\eta _{{t+1}}S_{{t}}$	$\displaystyle={\bf 1}_{{A^{c}}}(\varphi _{{t+1}}-\psi _{{t+1}})^{{\prime}}S_{{t}}+{\bf 1}_{{A}}(\frac{\zeta}{S_{{t}}^{{0}}},0,\dots,0)S_{{t}}=$
		$\displaystyle={\bf 1}_{{A^{c}}}(\varphi _{{t}}S_{{t}}-\psi _{{t}}S_{{t}})+{\bf 1}_{{A}}\zeta=V_{{t}}(\varphi)-V_{{t}}(\psi),$

zatem $\eta _{{t+1}}S_{{t}}=\eta _{{t}}S_{{t}}$ . Gdy $u>t$ , to

	$\displaystyle\eta _{{u}}S_{{u}}$	$\displaystyle=$	$\displaystyle[(\varphi _{{u}}-\psi _{{u}})S_{{u}}]{\bf 1}_{{A^{c}}}+{\bf 1}_{{A}}\frac{\zeta}{S_{{t}}^{{0}}}S_{{u}}^{{0}}=$
		$\displaystyle=$	$\displaystyle{\bf 1}_{{A^{c}}}(\varphi _{{u+1}}-\psi _{{u+1}})S_{{u}}+{\bf 1}_{A}\frac{\zeta}{S_{{t}}^{{0}}}S_{{u}}^{{0}}=\eta _{{u+1}}S_{{u}}.$

Czyli strategia $\eta$ jest samofinansująca się. Teraz sprawdzimy, że $\eta$ jest arbitrażem. Z założenia $0=V_{0}(\varphi)-V_{0}(\psi)=V_{0}(\eta)$ . Dalej, ponieważ strategie $\varphi,\psi$ replikują $X$ , więc

$V_{{T}}(\eta)={\bf 1}_{{A^{c}}}(\varphi _{{T}}-\psi _{{T}})S_{{T}}+{\bf 1}_{{A}}\frac{\zeta}{S_{{t}}^{{0}}}S_{{T}}^{{0}}={\bf 1}_{{A}}\frac{\zeta}{S_{{t}}^{{0}}}S_{{T}}^{{0}}\geq 0.$

Nieujemność wynika z dodatniości zmiennej losowej $\zeta$ na zbiorze $A$ i dodatniości $S^{0}$ . A ponieważ $P(V_{{T}}(\eta)>0)=P(A)>0$ , więc $\eta$ jest arbitrażem.

II. Przypadek $t=0$ zostawimy jako zadanie (ćw. 3.11).

∎

Implikacja odwrotna nie jest prawdziwa.

Ćwiczenie 3.2

Skonstruować rynek skończony, dla którego wszystkie wypłaty są jednoznacznie replikowalne i istnieje dodatnia wypłata $Y$ , dla której istnieje strategia $\varphi$ , taka że $V_{0}(\varphi)<0$ oraz $V_{{T}}(\varphi)=Y>0$ .

Wskazówka:

Patrz zad. (2.4).

Analogicznie do przypadku rynku dwustanowego wprowadzamy definicję ceny arbitrażowej.

Definicja 3.7

Niech ${\cal M}$ będzie rynkiem bez możliwości arbitrażu. Wtedy proces replikujący wypłaty osiągalnej $X$ nazywamy arbitrażową ceną $X$ na rynku ${\cal M}$ i oznaczamy przez $\Pi _{{t}}(X)$ , $t\in{\cal T}$ .

Uwaga 3.3

Z tw. 3.4 wynika, że cena arbitrażową $\Pi _{{t}}(X)$ wypłaty osiągalnej $X$ istnieje zawsze i jest wyznaczona jednoznacznie.

3.4. Zagadnienia i zadania na ćwiczenia

Ćwiczenie 3.3

Udowodnić uwagę 3.1, czyli:

	$\displaystyle\varphi\in\Phi$		$\displaystyle\Longleftrightarrow\quad V_{{t+1}}(\varphi)-V_{{t}}(\varphi)=\varphi _{{t+1}}(S_{{t+1}}-S_{{t}})\ \hbox{dla każdego $t$}$
			$\displaystyle\Longleftrightarrow\quad(\varphi _{{t+1}}-\varphi _{{t}})S_{{t}}=0\quad\hbox{dla każdego $t$}.$

Rozwiązanie:

	$\displaystyle V_{{t+1}}(\varphi)-V_{{t}}(\varphi)$	$\displaystyle=$	$\displaystyle\varphi _{{t+1}}S_{{t+1}}-\varphi _{{t+1}}S_{{t}}+\varphi _{{t+1}}S_{{t}}-\varphi _{{t}}S_{{t}}=$
		$\displaystyle=$	$\displaystyle\varphi _{{t+1}}(S_{{t+1}}-S_{t})+(\varphi _{{t+1}}-\varphi _{{t}})S_{{t}}.$

Ćwiczenie 3.4

Udowodnić, że strategia $\varphi$ polegająca na kupieniu za własne pieniądze $i$ -tej akcji w chwili 0, sprzedaniu jej w chwili $\tau$ , $\tau<T$ i włożeniu uzyskanych pieniędzy do banku jest samofinansująca się, gdy

a) $\tau$ jest ustaloną chwilą czasu,

b) $\tau$ jest momentem stopu.

Rozwiązanie:

Gdy $\tau\equiv u$ , to strategia $\varphi=\varphi^{{(u)}}$ ma postać

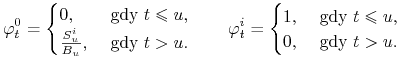$\varphi^{{0}}_{t}=\begin{cases}0,&\text{ gdy }t\leq u,\cr\frac{S^{i}_{u}}{B_{u}},&\text{ gdy }t>u.\end{cases}\qquad\varphi^{{i}}_{t}=\begin{cases}1,&\text{ gdy }t\leq u,\cr 0,&\text{ gdy }t>u.\end{cases}$

oraz $\varphi^{{j}}_{{t}}\equiv 0$ dla $j\not\in\{ 0,i\}$ . Wykażemy, że zachodzi (3.6). Istotnie,

$(\varphi _{{t+1}}-\varphi _{{t}})S_{{t}}=0$ dla $t\neq u$ , bo $\varphi _{{t+1}}-\varphi _{{t}}=0$ .

Dla $t=u$ , z definicji $\varphi$ , zachodzi $(\varphi _{{u+1}}-\varphi _{{u}})S_{{u}}=S_{{u}}^{i}-S_{{u}}^{i}=0.$

b) Ponieważ $\tau=\sum _{{k=0}}^{{T-1}}k{\bf 1}_{{\{\tau=k\}}}$ , więc $\varphi=\sum _{{k=0}}^{{T-1}}{\bf 1}_{{\{\tau=k\}}}\varphi^{{(k+1)}}$ . Zatem

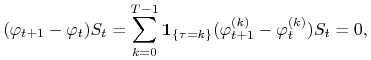$(\varphi _{{t+1}}-\varphi _{{t}})S_{{t}}=\sum _{{k=0}}^{{T-1}}{\bf 1}_{{\{\tau=k\}}}(\varphi^{{(k)}}_{{t+1}}-\varphi^{{(k)}}_{{t}})S_{t}=0,$

gdzie w ostatniej równości skorzystaliśmy z punktu a). Do sprawdzenia została prognozowalność procesu $\varphi$ .

Ćwiczenie 3.5

Na rynku istnieje możliwość arbitrażu wtedy i tylko wtedy, gdy istnieje portfel samofinansujący się $\varphi$ spełniający

$P(V_{T}^{*}(\varphi)\geq V_{0}(\varphi))=1,\quad P(V_{T}^{*}(\varphi)>V_{0}(\varphi))>0.$

Rozwiązanie:

$\Rightarrow$ oczywiste.
$\Leftarrow$ Gdy $\varphi$ ma własności podane w zadaniu, $\gamma=(V_{0}(\varphi),0,\dots,0)$ , to portfel $\psi=\varphi-\gamma$ jest portfelem arbitrażowym. Istotnie, $\psi\in\Phi$ , bogactwo początkowe

$V_{0}(\psi)=V_{0}(\varphi)-V_{0}(\gamma)=0$

oraz

$V_{T}^{*}(\psi)=V_{T}^{*}(\varphi)-V_{T}^{*}(\gamma)=V_{T}^{*}(\varphi)-V_{0}(\varphi),$

więc z własności portfela $\varphi$ mamy

$P(V_{T}^{*}(\psi)\geq 0)=1,\quad P(V_{T}^{*}(\psi)>0)>0.$

Ćwiczenie 3.6

Udowodnić, że gdy istnieje strategia $\varphi$ spełniająca $V_{0}(\varphi)<0$ i $\forall\omega\in\Omega$ zachodzi $V_{T}(\varphi)(\omega)\geq 0$ , to istnieje arbitraż.

Ćwiczenie 3.7

[ Prawo jednej ceny] Udowodnić, że na rynku bez możliwości arbitrażu portfele mające tę samą wartość w chwili $T$ muszą mieć tę samą wartość w chwili 0 (czyli muszą mieć tę samą cenę).

Rozwiązanie:

Niech $\varphi,\psi$ będą takie, że $V_{{T}}(\varphi)=V_{{T}}(\psi)$ . Załóżmy, nie wprost, że $V_{0}(\varphi)<V_{0}(\psi).$ Wtedy portfel $\kappa=\varphi-\psi$ spełnia $V_{0}(\kappa)=V_{0}(\varphi)-V_{0}(\psi)<0$ oraz $V_{T}(\kappa)=0$ , z czego wynika istnienie portfela arbitrażowego — sprzeczność z założeniem.

Z następnego zadania wynika, że na rynku bez możliwości arbitrażu wystarczy rozpatrywać jeden rachunek bankowy.

Ćwiczenie 3.8

Gdy na rynku $(S,\Phi)$ bez możliwości arbitrażu $S^{0}$ , $S^{1}$ są aktywami bez ryzyka, tj. $S^{1}$ też spełnia warunek (3.1) z pewnym $r_{1}$ , to $S^{0}=S^{1}$ .

Rozwiązanie:

Z założenia wynika, że $S^{1}_{t}=(1+r_{1})^{t}$ dla pewnego $r_{1}\geq 0$ . Gdy $r>r_{1}$ , to portfel $(1,-1,0,\dots,0)$ jest arbitrażem, a gdy $r<r_{1}$ , to portfel $(-1,1,0,\dots,0)$ jest arbitrażem.

Ćwiczenie 3.9

Podać przykład rynku bez możliwości arbitrażu i dwu różnych strategii samofinansujących się o tej samej wartości w chwili końcowej $T$ .

Rozwiązanie:

Przykład. Niech $T=1$ , stopa procentowa bez ryzyka wynosi 0% i na rynku są 2 akcje przyjmujące wartości:

	$\displaystyle S^{1}_{0}$	$\displaystyle=$	$\displaystyle 4,\quad S^{1}_{1}(\omega _{1})=5,\ S^{1}_{1}(\omega _{2})=3.$
	$\displaystyle S^{2}_{0}$	$\displaystyle=$	$\displaystyle 6,\quad S^{2}_{1}(\omega _{1})=7,\ S^{2}_{1}(\omega _{2})=5.$

Wtedy $\varphi=(5,5,0)$ i $\psi=(1,3,2)$ replikują tę samą wypłatę.

Ćwiczenie 3.10

Rozpatrzmy rynek jednookresowy z trzema możliwymi zdarzeniami losowymi. Inwestor uważa, że są one jednakowo prawdopodobne. Na rynku stopa procentowa bez ryzyka wynosi 20% i jest jedna akcja mająca proces cen postaci:

$S^{1}_{0}=25,\ S^{1}_{1}(\omega _{1})=20,\ S^{1}_{1}(\omega _{2})=40,\ S^{1}_{1}(\omega _{3})=35.$

Czy wszystkie wypłaty są na tym rynku osiągalne?

Ćwiczenie 3.11

Uzupełnić szczegóły drugiej części dowodu tw. 3.4.

Rozwiązanie:

Niech $t=0$ i niech $V_{0}(\varphi)>V_{0}(\psi)$ . Portfel

$\eta _{{u}}=(\psi _{{u}}-\varphi _{{u}})+(V_{0}(\varphi)-V_{0}(\psi),0,\dots,0)$

jest strategią samofinansującą się (kombinacja liniowa strategii samofinansujących się), dla której

$V_{0}(\eta)=V_{0}(\psi)-V_{0}(\varphi)+(V_{0}(\varphi)-V_{0}(\psi))S_{0}^{{0}}=0,$

bo $S_{0}^{{0}}=1$ , oraz

$V_{{T}}(\eta)=V_{{T}}(\psi)-V_{{T}}(\varphi)+(V_{0}(\varphi)-V_{0}(\psi))S_{{T}}^{{0}}=(V_{0}(\varphi)-V_{0}(\psi))S_{{T}}^{{0}}>0,$

więc $\eta$ jest arbitrażem, co kończy dowód.

Wynik ten jest też natychmiastową konsekwencją ćw. 3.7.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Modele matematyczne rynków instrumentów pochodnych I

Zagadnienia

3. Rynki skończone

3.1. Model rynku, portfel

Definicja 3.1

Definicja 3.2

Definicja 3.3

Twierdzenie 3.1

Uwaga 3.1

Ćwiczenie 3.1

Twierdzenie 3.2

3.2. Arbitraż

Definicja 3.4

Uwaga 3.2

Definicja 3.5

Twierdzenie 3.3

3.3. Wypłata europejska i jej wycena

Definicja 3.6

Twierdzenie 3.4

Ćwiczenie 3.2

Definicja 3.7

Uwaga 3.3

3.4. Zagadnienia i zadania na ćwiczenia

Ćwiczenie 3.3

Ćwiczenie 3.4

Ćwiczenie 3.5

Ćwiczenie 3.6

Ćwiczenie 3.7

Ćwiczenie 3.8

Ćwiczenie 3.9

Ćwiczenie 3.10

Ćwiczenie 3.11