Zagadnienia
7. Opcje amerykańskie
Dotąd
rozpatrywane wypłaty (opcje typu europejskiego) były typu
statycznego, czyli wypłata z opcji następuje w ustalonej chwili ![]() .
Teraz rozszerzymy pojęcie instrumentu pochodnego na opcje
amerykańskie, czyli na instrument dający posiadaczowi prawo
realizacji w dowolnej chwili
.
Teraz rozszerzymy pojęcie instrumentu pochodnego na opcje
amerykańskie, czyli na instrument dający posiadaczowi prawo
realizacji w dowolnej chwili ![]() .
.
7.1. Opcje amerykańskie, wycena, zabezpieczenie
Definicja 7.1
Opcją amerykańską o terminie
wygaśnięcia ![]() nazywamy ciąg adaptowanych nieujemnych zmiennych
losowych
nazywamy ciąg adaptowanych nieujemnych zmiennych
losowych ![]() ,
, ![]() .
.
Zmienną losową ![]() interpretujemy jako wypłatę otrzymaną
z realizacji opcji amerykańskiej w chwili
interpretujemy jako wypłatę otrzymaną
z realizacji opcji amerykańskiej w chwili ![]() , a ponieważ
, a ponieważ ![]() jest
jest
![]() -mierzalne, to wypłata zależy od wiedzy w chwili
-mierzalne, to wypłata zależy od wiedzy w chwili ![]() .
.
Przykład 7.1
Amerykańska opcja kupna na akcję
o cenie ![]() z ceną wykonania
z ceną wykonania ![]() (dodatnia stała) zadana jest przez
(dodatnia stała) zadana jest przez
![]() ,
, ![]() . Kupujący otrzymuje prawo do
zakupu akcji po cenie
. Kupujący otrzymuje prawo do
zakupu akcji po cenie ![]() w dowolnej chwili
w dowolnej chwili ![]() .
Analogicznie ciąg
.
Analogicznie ciąg ![]() ,
, ![]() , zadaje
amerykańską opcję sprzedaży na
akcje o cenie
, zadaje
amerykańską opcję sprzedaży na
akcje o cenie ![]() z ceną wykonania
z ceną wykonania ![]() .
.
Posiadacz opcji amerykańskiej ma prawo wykonać ją w dowolnej chwili.
Ponieważ posiadacz opcji decyduje czy chwila jej wykonania właśnie
nastąpiła i decyduje na podstawie wiedzy zebranej do tego momentu,
więc ![]() , a więc moment wykonania opcji
, a więc moment wykonania opcji
![]() jest momentem stopu. Sprzedawca opcji dostając za nią zapłatę
jest momentem stopu. Sprzedawca opcji dostając za nią zapłatę
![]() musi postępować w taki sposób, aby w każdej chwili wartość
jego portfela
musi postępować w taki sposób, aby w każdej chwili wartość
jego portfela ![]() o kapitale początkowym
o kapitale początkowym ![]() przewyższała
jego zobowiązania wobec kupca opcji, czyli strategia
przewyższała
jego zobowiązania wobec kupca opcji, czyli strategia ![]() musi
być taka, by dla wszystkich
musi
być taka, by dla wszystkich ![]() zachodziło:
zachodziło:
| (7.1) |
Strategię ![]() spełniająca (7.1) nazywamy strategią
zabezpieczającą opcję
amerykańską
spełniająca (7.1) nazywamy strategią
zabezpieczającą opcję
amerykańską
![]() . Zbiór wszystkich takich strategii będziemy
oznaczali przez
. Zbiór wszystkich takich strategii będziemy
oznaczali przez ![]() Z warunku
(7.1) wynika, że
Z warunku
(7.1) wynika, że
dla
dowolnego momentu stopu ![]() o wartościach w zbiorze
o wartościach w zbiorze ![]() .
Korzystając z analogicznych argumentów jak przy definiowaniu ceny
sprzedającego przyjmujemy:
.
Korzystając z analogicznych argumentów jak przy definiowaniu ceny
sprzedającego przyjmujemy:
Definicja 7.2
Wielkość
| (7.2) |
nazywamy ceną arbitrażową w chwili ![]() opcji amerykańskiej zadanej
przez ciąg wypłat
opcji amerykańskiej zadanej
przez ciąg wypłat ![]() .
.
Naszym celem będzie teraz znalezienie ceny ![]() Załóżmy, że rozpatrywany
rynek jest skończony, bez możliwości arbitrażu i zupeły z jednym instrumentem
ryzykownym, czyli
Załóżmy, że rozpatrywany
rynek jest skończony, bez możliwości arbitrażu i zupeły z jednym instrumentem
ryzykownym, czyli ![]() .
Przez
.
Przez ![]() będziemy oznaczać cenę opcji amerykańskiej w chwili
będziemy oznaczać cenę opcji amerykańskiej w chwili ![]() .
Zatem naszym zadaniem jest znalezienie
.
Zatem naszym zadaniem jest znalezienie ![]() . W tym celu skorzystamy z tego, że w chwili
. W tym celu skorzystamy z tego, że w chwili ![]() zachodzi
zachodzi
![]() i wykorzystamy indukcję wsteczną.
W chwili
i wykorzystamy indukcję wsteczną.
W chwili ![]() wystawca opcji musi mieć taki
kapitał, by zabezpieczyć jedną z wypłat: wypłatę
wystawca opcji musi mieć taki
kapitał, by zabezpieczyć jedną z wypłat: wypłatę ![]() w chwili
w chwili
![]() albo wypłatę
albo wypłatę ![]() w chwili
w chwili ![]() , gdyż każdą z nich może wybrać
nabywca opcji. Ponieważ rynek jest zupełny, więc wypłata
, gdyż każdą z nich może wybrać
nabywca opcji. Ponieważ rynek jest zupełny, więc wypłata ![]() w chwili
w chwili ![]() jest osiągalna i w chwili
jest osiągalna i w chwili ![]() jej cena
jest równa
jej cena
jest równa ![]() —
tyle trzeba mieć w chwili
—
tyle trzeba mieć w chwili ![]() , by zabezpieczyć wypłatę
, by zabezpieczyć wypłatę ![]() w chwili
w chwili ![]() . Stąd cena opcji amerykańskiej w chwili
. Stąd cena opcji amerykańskiej w chwili ![]() wynosi:
wynosi:
Analogiczne rozumowanie daje cenę opcji amerykańskiej w chwili ![]() :
:
| (7.3) |
dla ![]() , gdyż wystawca musi zabezpieczyć jedną
z wypłat: natychmiastową w chwili
, gdyż wystawca musi zabezpieczyć jedną
z wypłat: natychmiastową w chwili ![]() , tj. wypłatę
, tj. wypłatę ![]() lub
wypłatę w chwili późniejszej, a ona w chwili
lub
wypłatę w chwili późniejszej, a ona w chwili ![]() jest warta
jest warta ![]() .
Dzieląc obie strony przez
.
Dzieląc obie strony przez ![]() i oznaczając
i oznaczając
![]() mamy
mamy
| (7.4) |
Zatem otrzymaliśmy
Twierdzenie 7.1
Zdyskontowana cena ![]() opcji
amerykańskiej zadanej przez ciąg wypłat
opcji
amerykańskiej zadanej przez ciąg wypłat ![]() jest
jest ![]() -nadmartyngałem zadanym wzorem (7.4).
-nadmartyngałem zadanym wzorem (7.4).
Ze wzoru (7.4) wynika, że ciąg ![]() jest obwiednią Snella ciągu
jest obwiednią Snella ciągu
![]() , czyli że
, czyli że ![]() jest najmniejszym
jest najmniejszym
![]() -nadmartyngałem dominującym ciąg
-nadmartyngałem dominującym ciąg ![]() .
Stąd wykorzystując elementy teorii optymalnego stopowania mamy
.
Stąd wykorzystując elementy teorii optymalnego stopowania mamy
Twierdzenie 7.2
-
a)
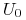 — cena w chwili
— cena w chwili 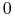 opcji amerykańskiej spełnia
opcji amerykańskiej spełnia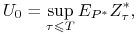
(7.5) gdzie
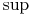 bierzemy po momentach stopu
bierzemy po momentach stopu 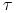 o wartościach mniejszych lub
równych
o wartościach mniejszych lub
równych 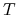 .
. -
b) Istnieje strategia samofinansująca się
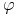 o kapitale
początkowym
o kapitale
początkowym 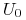 zabezpieczająca wypłatę z opcji amerykańskiej
zabezpieczająca wypłatę z opcji amerykańskiej
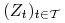 .
. -
c) Moment stopu
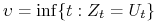
(7.6) jest momentem realizacji opcji.
Punkt a). Zdyskontowany proces ceny opcji amerykańskiej ![]() jest obwiednią Snella ciągu zdyskontowanych wypłat
jest obwiednią Snella ciągu zdyskontowanych wypłat ![]() , a stąd
korzystając z teorii optymalnego stopowania wynika
(7.5).
, a stąd
korzystając z teorii optymalnego stopowania wynika
(7.5).
Punkt b).
Jak wiemy, ![]() jest
jest ![]() –nadmartyngałem, więc
z tw. Dooba-Meyera o rozkładzie
nadmartyngału
–nadmartyngałem, więc
z tw. Dooba-Meyera o rozkładzie
nadmartyngału
| (7.7) |
gdzie ![]() jest martyngałem,
jest martyngałem, ![]() — procesem rosnącym
prognozowalnym,
— procesem rosnącym
prognozowalnym, ![]() . Rynek jest zupełny,
więc istnieje strategia
. Rynek jest zupełny,
więc istnieje strategia ![]() taka, że
taka, że ![]() .
Ponieważ
.
Ponieważ ![]() jest martyngałem, więc
jest martyngałem, więc
Stąd i z (7.7) mamy ![]() , czyli
, czyli ![]() jest kapitałem początkowym strategii
jest kapitałem początkowym strategii ![]() . Ponadto
. Ponadto
![]() czyli
czyli
| (7.8) |
a ponieważ ![]() , proces
, proces ![]() dominuje
dominuje ![]() , więc
, więc
czyli ![]() zabezpiecza opcję amerykańską.
zabezpiecza opcję amerykańską.
Punkt c). Mając opcję nie ma sensu realizować jej
w chwili ![]() takiej, że
takiej, że ![]() , bo sprzedajemy walor wart
, bo sprzedajemy walor wart ![]() za cenę
za cenę ![]() (lepiej opcję sprzedać za
(lepiej opcję sprzedać za ![]() niż ją zrealizować
i otrzymać
niż ją zrealizować
i otrzymać ![]() ). Stąd moment realizacji opcji (moment stopu)
). Stąd moment realizacji opcji (moment stopu)
![]() spełnia
spełnia
gdyż wiemy, że ![]() . Nie ma sensu realizować opcji po
chwili
. Nie ma sensu realizować opcji po
chwili
gdyż sprzedając opcję w chwili ![]() i kupując strategię
zabezpieczającą
i kupując strategię
zabezpieczającą ![]() otrzymamy
otrzymamy
i od tego momentu postępując zgodnie ze strategią ![]() mamy
portfel, którego bogactwo jest większe niż wartość opcji w chwili
mamy
portfel, którego bogactwo jest większe niż wartość opcji w chwili
![]() . Istotnie, ponieważ (7.8)
implikuje
. Istotnie, ponieważ (7.8)
implikuje
oraz ![]() dla
dla ![]() , więc
, więc ![]() dla
dla
![]() . Zatem
. Zatem ![]() . Pozwala to
stwierdzić, że
. Pozwala to
stwierdzić, że ![]() jest martyngałem, gdyż wtedy
jest martyngałem, gdyż wtedy ![]() (bo
(bo ![]() ) i korzystamy
z przedstawienia (7.7).
Stąd wynika, że dla nabywcy opcji najlepszym momentem realizacji
opcji jest optymalny moment stopu dla ciągu
) i korzystamy
z przedstawienia (7.7).
Stąd wynika, że dla nabywcy opcji najlepszym momentem realizacji
opcji jest optymalny moment stopu dla ciągu ![]() przy
rozkładzie prawdopodobieństwa
przy
rozkładzie prawdopodobieństwa ![]() (korzystamy z tw.
charakteryzującego moment
optymalny). A jak wiadomo moment stopu zdefiniowany wzorem
(7.6) ma taką własność.
(korzystamy z tw.
charakteryzującego moment
optymalny). A jak wiadomo moment stopu zdefiniowany wzorem
(7.6) ma taką własność.
Uwaga 7.1
a) Z tw. 7.2 mamy, że
czyli cena zdefiniowana wzorem (7.2) satysfakcjonuje
także kupującego. Kupujący chce najlepiej wykorzystać swoje prawa
i uzyskać jak największą wypłatę. Gdy kupujący realizuje opcję
w momencie stopu ![]() i otrzymuje wypłatę
i otrzymuje wypłatę ![]() , to jest
skłonny zapłacić za tę wypłatę
, to jest
skłonny zapłacić za tę wypłatę ![]() . A ponieważ
kupujący może zrealizować opcję w każdym momencie, więc za uczciwą
cenę uważa
. A ponieważ
kupujący może zrealizować opcję w każdym momencie, więc za uczciwą
cenę uważa ![]() , gdzie supremum bierzemy
po momentach stopu
, gdzie supremum bierzemy
po momentach stopu ![]() o wartościach mniejszych lub równych
o wartościach mniejszych lub równych ![]() .
.
b) Punkt c) twierdzenia odpowiada na zasadnicze pytanie z punktu
widzenia nabywcy: kiedy należy zrealizować opcję.
Z dowodu tego punktu wynika, że moment wykonania opcji należy
wybrać jako optymalny moment stopu dla problemu optymalnego
stopowania ciągu ![]() . Taki moment nie jest wyznaczony
jednoznacznie. Jednym z takich momentów jest moment zdefiniowany
wzorem (7.6). Wybieramy go, gdyż (7.6),
daje jego jawną postać. Mamy regułę jak ten moment wyznacznaczyć
praktycznie.
. Taki moment nie jest wyznaczony
jednoznacznie. Jednym z takich momentów jest moment zdefiniowany
wzorem (7.6). Wybieramy go, gdyż (7.6),
daje jego jawną postać. Mamy regułę jak ten moment wyznacznaczyć
praktycznie.
Wykorzystując dowód punktu c) twierdzenia możemy zanalizować
sytuacje wystawcy opcji. Wystawca opcji stosuje strategię ![]() i czeka na to, co zrobi nabywca. Jeżeli nabywca zrealizuje opcję
w chwili optymalnej
i czeka na to, co zrobi nabywca. Jeżeli nabywca zrealizuje opcję
w chwili optymalnej ![]() , to
, to ![]() .
Wtedy sprzedawca stosując strategię
.
Wtedy sprzedawca stosując strategię ![]() otrzymuje całą kwotę,
którą musi wypłacić nabywcy opcji. Sprzedawca zabezpieczył swoje
zobowiązanie wobec nabywcy.
Jeśli natomiast nabywca zrealizuje opcję w innej
chwili
otrzymuje całą kwotę,
którą musi wypłacić nabywcy opcji. Sprzedawca zabezpieczył swoje
zobowiązanie wobec nabywcy.
Jeśli natomiast nabywca zrealizuje opcję w innej
chwili ![]() niż optymalna
niż optymalna ![]() , to wystawca ma dodatni zysk.
Istotnie, gdy moment realizacji
, to wystawca ma dodatni zysk.
Istotnie, gdy moment realizacji ![]() nie jest optymalny, to
nie jest optymalny, to
![]() lub
lub ![]() i korzystając
z (7.8) otrzymujemy zysk wystawcy:
i korzystając
z (7.8) otrzymujemy zysk wystawcy:
7.2. Porównanie opcji amerykańskich i europejskich
Zajmiemy się teraz porównaniem opcji amerykańskich i europejskich. Opcje amerykańskie dają posiadaczowi więcej praw niż europejskie, więc powinny kosztować więcej.
Twierdzenie 7.3
Niech ![]() będzie wartością w chwili
będzie wartością w chwili ![]() opcji
amerykańskiej zadanej przez ciąg
opcji
amerykańskiej zadanej przez ciąg ![]() , a
, a ![]() wartością
w chwili
wartością
w chwili ![]() opcji europejskiej o wypłacie
opcji europejskiej o wypłacie
![]() . Wtedy
. Wtedy
| (7.9) |
Ponadto, gdy dla każdego ![]() mamy
mamy
| (7.10) |
to dla każdego ![]() mamy
mamy
| (7.11) |
Ponieważ ![]() jest
jest ![]() -nadmartyngałem oraz
-nadmartyngałem oraz ![]() , więc
, więc
Stąd ![]() , czyli zachodzi warunek (7.9).
Z warunku (7.10) wynika, że
, czyli zachodzi warunek (7.9).
Z warunku (7.10) wynika, że ![]() , a ponieważ
, a ponieważ
![]() jest
jest ![]() -martyngałem, w szczególności
-martyngałem, w szczególności
![]() -nadmartyngałem, więc
-nadmartyngałem, więc
| (7.12) |
bowiem ![]() jest najmniejszym nadmartyngałem
dominującym
jest najmniejszym nadmartyngałem
dominującym ![]() . Teraz (7.9) i (7.12)
dają (7.11).
. Teraz (7.9) i (7.12)
dają (7.11).
Z tw. 7.3 wynika, że amerykańska opcja kupna jest warta tyle samo, co europejska..
Wniosek 7.1
Ceny amerykańskiej i europejskiej opcji kupna z tym samym terminem wygaśnięcia i tę samą cena wykonania są równe.
Ogólniejszą wersję wniosku można znaleźć w ćw. 7.5.
Przykład 7.2
Na rynku zupełnym opisanym w przykł. 4.2 chcemy znaleźć ceny
amerykańskiej opcji kupna i amerykańskiej opcji sprzedaży z ceną
wykonania ![]() , a także znaleźć optymalny momentem wykonania
opcji sprzedaży przez nabywcę opcji.
, a także znaleźć optymalny momentem wykonania
opcji sprzedaży przez nabywcę opcji.
Jak wiemy, cena amerykańskiej opcji kupna jest równa cenie opcji
europejskiej (tw. 7.3), więc korzystając z przykł.
4.2 otrzymujemy ![]() . Obliczymy cenę
amerykańskiej opcji sprzedaży. Korzystamy ze wzoru (7.3)
kolejno dla
. Obliczymy cenę
amerykańskiej opcji sprzedaży. Korzystamy ze wzoru (7.3)
kolejno dla ![]() i
i ![]() , otrzymując:
, otrzymując:
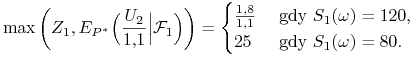 |
||||
Moment stopu zdefiniowany wzorem
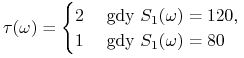 |
jest optymalnym momentem wykonania opcji sprzedaży przez jej posiadacza.
7.3. Zagadnienia i zadania na ćwiczenia
Ćwiczenie 7.1
Bank ma amerykańską opcję sprzedaży akcji z ceną realizacji 60
i datą wygaśnięcia za ![]() roku. Walor (akcja) wart jest teraz 6,
a stopa procentowa bez ryzyka (kapitalizacja ciągła) wynosi
roku. Walor (akcja) wart jest teraz 6,
a stopa procentowa bez ryzyka (kapitalizacja ciągła) wynosi ![]() p.a.1skrót łac. per annum, w skali roku. Czy warto
opcję zrealizować teraz, czy w chwili wygaśnięcia?
p.a.1skrót łac. per annum, w skali roku. Czy warto
opcję zrealizować teraz, czy w chwili wygaśnięcia?
Teraz mamy ![]() , wkładamy do banku i za
, wkładamy do banku i za ![]() roku mamy
roku mamy
![]() . W chwili wygaśnięcia
opcja jest warta co najwyżej 60 (gdy
. W chwili wygaśnięcia
opcja jest warta co najwyżej 60 (gdy ![]() ). Zatem warto opcję
zrealizować teraz. Wynika to z faktu, że cena waloru jest niska
w porównaniu z ceną wykonania opcji. W takim przypadku wykonujemy
opcję i inwestujemy otrzymane pieniądze.
). Zatem warto opcję
zrealizować teraz. Wynika to z faktu, że cena waloru jest niska
w porównaniu z ceną wykonania opcji. W takim przypadku wykonujemy
opcję i inwestujemy otrzymane pieniądze.
Ćwiczenie 7.2
Mówimy, że opcja amerykańska ![]() jest zawsze
realizowalna, gdy dla dowolnego momentu stopu
jest zawsze
realizowalna, gdy dla dowolnego momentu stopu ![]() o wartościach
mniejszych lub równych
o wartościach
mniejszych lub równych ![]() istnieje strategia
istnieje strategia ![]() taka,
że
taka,
że
Udowodnić, że na rynku zupełnym każda opcja amerykańska jest zawsze realizowalna.
Ustalmy dowolny moment stopu ![]() . Na mocy zupełności rynku
wypłata
. Na mocy zupełności rynku
wypłata
jest osiągalna, więc istnieje ![]() takie, że
takie, że
![]() . Stąd
. Stąd
a więc
czyli ![]() .
.
Ćwiczenie 7.3
Udowodnić, że gdy na rynku zupełnym opcja amerykańska jest wyceniana wzorem (7.5), to
a) nie istnieje arbitraż związany z pozycją krótką (tj. wystawcy opcji),
b) nie istnieje arbitraż związany z pozycją długą (tj. nabywcy opcji).
a) Nie wprost. Gdyby istniał arbitraż związany z pozycją
krótką, to sprzedawca posługiwałby się portfelem ![]() zabezpieczającym opcję amerykańską takim, że dla każdego momentu
wykonania opcji przez kupującego, tj. momentu stopu
zabezpieczającym opcję amerykańską takim, że dla każdego momentu
wykonania opcji przez kupującego, tj. momentu stopu ![]() , ma on
zysk bez ryzyka:
, ma on
zysk bez ryzyka:
Wtedy
dla każdego momentu stopu ![]() , co na mocy skończoności
, co na mocy skończoności ![]() implikuje
implikuje
sprzeczność.
Ćwiczenie 7.4
Niech w modelu CRR: ![]()
![]()
![]() . Znaleźć cenę w chwili 0 opcji amerykańskiej o wypłacie
. Znaleźć cenę w chwili 0 opcji amerykańskiej o wypłacie
![]() (jest tzw. opcja rosyjska.
Znaleźć moment wykonania opcji. Znaleźć dla niej strategię
zabezpieczającą.
(jest tzw. opcja rosyjska.
Znaleźć moment wykonania opcji. Znaleźć dla niej strategię
zabezpieczającą.
Z danych wynika, że rynek jest wolny od arbitrażu. Miara
martyngałowa ![]() jest wyznaczona przez
jest wyznaczona przez ![]() .
.
Znajdujemy wartość wypłaty ![]() dla każdej
ścieżki, a następnie obliczamy cenę:
dla każdej
ścieżki, a następnie obliczamy cenę: ![]() .
.
![]() . Moment
. Moment
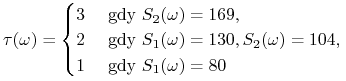 |
jest optymalnym momentem wykonania opcji przez posiadacza. Strategię zabezpieczającą znajdujemy korzystając np. z tw. 7.2 i postaci martyngału w rozkładzie Dooba
Ćwiczenie 7.5
Niech ciąg ![]() , gdzie
, gdzie ![]() jest funkcją wypukłą,
nieujemną,
jest funkcją wypukłą,
nieujemną, ![]() , zadaje opcję amerykańską na rynku zupełnym.
Udowodnić, że cena tej opcji amerykańskiej jest równa cenie opcji
europejskiej o wypłacie
, zadaje opcję amerykańską na rynku zupełnym.
Udowodnić, że cena tej opcji amerykańskiej jest równa cenie opcji
europejskiej o wypłacie ![]() .
.




