Zagadnienia
1. Przedmiot wykładu. Ogólna teoria wyboru
1.1. Literatura
Notacja skryptu jest w większości zgodna z użytą w podręczniku [1].
Dla tych, którzy chcą poczytać coś łatwego, przyjemnego i po polsku, poznać intuicje polecam Variana [3]
1.2. Mikroekonomia – co się pod tym kryje
Mikroekonomia – matematycznie sformalizowany dział ekonomii opisujący podejmowanie decyzji przez jednostki (m.in konsumentów i producentów) oraz zagadnienia równowagi związane z interakcjami tychże podejmujących decyzje (modele rynków). Zwykłemu ”przeciętnemu śmiertelnikowi” słowo ”ekonomia” kojarzy się przeważnie na jeden z czterech sposobów jako:
1) sposób na zarobienie dużych pieniędzy (oczywiście bez ponoszenia ryzyka);
2) kolumny cyferek, które dodają księgowi, aby na końcu
uzyskać ”winien ![]() ma”;
ma”;
3) zbiór magicznych reguł określający, jak w reakcji na określone działania polityków zachowa się gospodarka (cokolwiek by to słowo znaczyło), a co za tym idzie: czy będę miał pracę, ile zapłacę za benzynę…
4) wielkie oszustwo, którym politycy usprawiedliwiają swoje błędy.
żaden z tych opisów nie tylko nie obejmuje mikroekonomii, ale nawet nie ma z nią niepustego przecięcia: (1) to finanse, (a raczej fikcja o finansach, jako że podstawową prawdą w ekonomii jest słynne ”no free lunch”, czyli ”nie ma czegoś takiego, jak obiadek za darmo”); (2) to rachunkowość, a (3) i (4) to makroekonomia.
Z punktu widzenia matematyka to właśnie mikroekonomia jest najciekawszą dziedziną ekonomii: jest najbardziej zmatematyzowana (oczywiście poza rachunkowością, ale trudno matematykę w rachunkowości uznać za ciekawą).
Mikroekonomia nie odpowiada na pytania ”jak zachowa się gospodarka” ani ”co zrobić, żeby zarobić”.
Opisuje zachowanie jednostek: ludzi lub firm (najczęściej nazywanych konsumentami i producentami, choć będziemy też używać takich określeń jak agent czy gracz, w rozumieniu znacznie szerszym niż potoczne) i określa, jak skumulowane (w ekonomii używamy terminu ”zagregowane” do określenia wielkości skumulowanych, łącznych; i czasownika ”agregować”) efekty indywidualnych decyzji prowadzą do równowagi.
Tak więc całą mikroekonomię w uproszczeniu można sprowadzić do dwóch zagadnień: teorii wyboru i równowagi.
Naszą analizę rozpoczniemy od teorii wyboru.
1.3. Ogólna teoria wyboru
W ogólnej teorii wyboru mamy jednego podejmującego decyzje (zamiennie używa się pochodzącego z angielskiego terminu agent). Wybiera on ze zbioru możliwości, przy czym w konkretnej sytuacji musi ograniczyć się jedynie do aktualnie dostępnego zbioru budżetowego.
Zbiór możliwości ![]() w najbardziej ogólnej
postaci zawiera wszystkie fizycznie osiągalne wektory o współrzędnych oznaczających wszystko, co może mieć wartość dla
podejmującego decyzję: konsumpcja, wolny czas, pieniądze,
udział w loteriach, zysk, oszczędności na przyszłość
itd. Można to ciągnąć w nieskończoność.
Zazwyczaj jednak ograniczymy się do skończenie wymiarowego zbioru
możliwości i to niewielkiego wymiaru, czyli przyjmiemy, że w
konkretnym zadaniu decyzyjnym bierzemy pod uwagę tylko niektóre
czynniki, redukując złożoność nawet do dwóch
wymiarów – interesujące nas w danej analizie dobro i pieniądze
na zakup innych.
w najbardziej ogólnej
postaci zawiera wszystkie fizycznie osiągalne wektory o współrzędnych oznaczających wszystko, co może mieć wartość dla
podejmującego decyzję: konsumpcja, wolny czas, pieniądze,
udział w loteriach, zysk, oszczędności na przyszłość
itd. Można to ciągnąć w nieskończoność.
Zazwyczaj jednak ograniczymy się do skończenie wymiarowego zbioru
możliwości i to niewielkiego wymiaru, czyli przyjmiemy, że w
konkretnym zadaniu decyzyjnym bierzemy pod uwagę tylko niektóre
czynniki, redukując złożoność nawet do dwóch
wymiarów – interesujące nas w danej analizie dobro i pieniądze
na zakup innych.
Rodzina zbiorów budżetowych ![]() to rodzina niepustych
podzbiorów zbioru możliwości zawierających punkty osiągalne przy pewnych ograniczeniach (np. chociaż doba ma 24 godziny, to mogę pracować nie więcej niż 12; mam 100 złotych i przy
danych cenach nie mogę kupić towarów za więcej).
to rodzina niepustych
podzbiorów zbioru możliwości zawierających punkty osiągalne przy pewnych ograniczeniach (np. chociaż doba ma 24 godziny, to mogę pracować nie więcej niż 12; mam 100 złotych i przy
danych cenach nie mogę kupić towarów za więcej).
Przykład 1.1 (Walrasowskie albo konkurencyjne albo rynkowe zbiory budżetowe 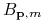 )
)
Najczęściej w wyborze konsumenta mamy do czynienia z sytuacją,
gdy na rynku jest ![]() dóbr (
dóbr (![]() , czyli
, czyli ![]() ), dany jest wektor cen rynkowych
), dany jest wektor cen rynkowych ![]() , a my mamy do
dyspozycji określony dochód
, a my mamy do
dyspozycji określony dochód ![]() do wydania. Wówczas zbiór
budżetowy ma postać
do wydania. Wówczas zbiór
budżetowy ma postać ![]() .
.
Ćwiczenie 1.1
Zobaczyć, jak zmnieni się Walrasowski zbiór budżetowy na płaszczyźnie przy
a) wzroście ceny dobra ![]() ,
,
b) wzroście dochodu,
c) równoczesnym wzroście cen obu dóbr przy zachowaniu ich relacji.
Ćwiczenie 1.2
Jaką postać będzie miał zbiór budżetowy, jeśli na pierwotny Walrasowski zbiór budżetowy ![]() na płaszczyźnie nałożymy dodatkowe ograniczenia.
na płaszczyźnie nałożymy dodatkowe ograniczenia.
a) Fundusz celowy (na przykład na żywność, ubranka dziecięce czy wykształecenie) – z posiadanego majątku ![]() kwota
kwota ![]() może być wydana tylko na
może być wydana tylko na ![]() .
.
b) Reglamentacja pewnego dobra czyli kartki (na mięso, benzynę itd) – ścisła reglamentacja.
Nie można kupić więcej ![]() niż
niż ![]() (tyle, ile na kartce).
(tyle, ile na kartce).
c) Reglamentacja pewnego dobra czyli kartki – nieścisła reglamentacja (na przykład z czarnym rynkiem albo specjalnymi sklepami ”wolnorynkowymi”).
Mogę konsumować więcej ![]() niż
niż ![]() , ale za nadwyżkę ponad
, ale za nadwyżkę ponad ![]() płacę
płacę ![]() .
.
d) Jedno lub oba dobra konsumowane w całkowitych ilościach.
e) Dobra, których konsumpcja wzajemnie się wyklucza.
Ćwiczenie 1.3
Zapisać jako Walrasowski zbiór budżetowy zagadnienia podaży pracy.
Mam do dyspozycji ![]() godzin do podziału na pracę
godzin do podziału na pracę ![]() i czas wolny
i czas wolny ![]() . Za godzinę pracy otrzymuję stawkę płacy
. Za godzinę pracy otrzymuję stawkę płacy ![]() . Zarobione pieniądze przeznaczam na zakup dóbr konsumpcyjnych
. Zarobione pieniądze przeznaczam na zakup dóbr konsumpcyjnych ![]() (dla uproszczenia o cenie
(dla uproszczenia o cenie ![]() ).
).
Spróbować zinterpretować ekonomiczne znaczenie zmiennych występujących w równaniu.
Rozważane dobra to czas wolny i pieniądze na konsumpcję.
Zinterpretować ![]() ,
, ![]() i
i ![]() można na podstawie tego, w jakich miejscach znalazły się w nierówności – odpoczynek jest dobrem, które kupuję po cenie
można na podstawie tego, w jakich miejscach znalazły się w nierówności – odpoczynek jest dobrem, które kupuję po cenie ![]() , a mój majątek to wartość pieniężna mojego czasu.
, a mój majątek to wartość pieniężna mojego czasu.
Ćwiczenie 1.4
Jak zmieni się Walrasowski zbiór budżetowy zagadnienia podaży pracy w następujących sytuacjach.
a) Ograniczenie urzędowe czasu pracy typu ”co najmniej” lub ”co najwyżej”.
b) Wyższą płaca za nadgodziny: za czas pracy powyżej pewnego ![]() – ustawowego czasu pracy – dostaję stawkę płacy
– ustawowego czasu pracy – dostaję stawkę płacy ![]() .
.
c) Podatek dochodowy progresywny z progiem: w uproszczeniu od kwoty powyżej pewnego ![]() (kwota, powyżej której łapię się na wyższy próg) płacę podatek o stawce
(kwota, powyżej której łapię się na wyższy próg) płacę podatek o stawce ![]() .
.
Ćwiczenie 1.5
Wybór międzyokresowy dla doskonałego systemu finansowego ”bez tarcia” jako Walrasowski zbiór budżetowy.
Dziś zarabiam ![]() , a za rok
, a za rok ![]() i jest to z góry wiadome. Podejmuję decyzję co do konsumpcji dziś
i jest to z góry wiadome. Podejmuję decyzję co do konsumpcji dziś ![]() i za rok
i za rok ![]() . Mogę swobodnie pożyczać z banku (pod warunkiem, że oddam) lub lokować pieniądze przy tej samej stopie procentowej
. Mogę swobodnie pożyczać z banku (pod warunkiem, że oddam) lub lokować pieniądze przy tej samej stopie procentowej ![]() .
.
Zapisać dwie nierówności określające mój zbiór budżetowy, które mają oczywistą interpretację.
Te dwie nierówności to nierówności z użyciem wartości przyszłej i wartości bieżącej (z dyskontowaniem).
Ćwiczenie 1.6
Ewolucja rynku finansowego od zera do doskonałego, czyli narysować kolejne zbiory budżetowe.
a) Mieszkam na bezludnej wyspie a mój zarobek jest w główkach kapusty – czego nie zjem, to się zmarnuje.
b) Mieszkam na bezludnej wyspie a mój zarobek jest w kokosach – mogę je przechować.
c) Mieszkam na bezludnej wyspie a mój zarobek jest w zbożu, które mogę zasiać – wówczas za rok od każdego posianego ziarna dostanę ![]() ziaren.
ziaren.
d) Mieszkam we współczesnej Polsce i mogę korzystać z banku, który pobiera prowizję, tak że stopa lokat ![]() jest mniejsza niż stopa kredytów
jest mniejsza niż stopa kredytów ![]() .
.
Z każdego zbioru budżetowego agent wybiera przynajmniej jeden punkt… Jeżeli dodamy ”tak, aby wybrane punkty były dla niego najlepsze”, to przejdziemy do jednego z dwóch ujęć teorii wyboru: podejścia maksymalizacji preferencji. Jeżeli natomiast postawimy kropkę, a interesować nas będzie jedynie funkcja (przeważnie będzie to odwzorowanie wielowartościowe) przyporządkowująca zbiorowi budżetowemu wybór – nieważne skąd się wziął – to będzie to podejście struktury wyboru (w którym mieszczą się znane na pewno ze słyszenia terminy popyt i podaż).
1.3.1. Podejście maksymalizacji preferencji / użyteczności
Teoria preferencji to matematyczne sformalizowanie zdania ”agent wybiera najlepszą z dostępnych możliwości”.
Definicja 1.1
Relację dwuargumentową ![]() określoną na zbiorze
możliwości
określoną na zbiorze
możliwości ![]() będziemy nazywać relacją
preferencji (albo relacją słabej preferencji).
będziemy nazywać relacją
preferencji (albo relacją słabej preferencji).
Relację ścisłej preferencji![]() definiujemy przy
pomocy relacji preferencji wzorem
definiujemy przy
pomocy relacji preferencji wzorem ![]()
![]() .
.
Relację obojętności![]() definiujemy wzorem
definiujemy wzorem ![]() .
.
Zamiast ![]() , będziemy pisać
, będziemy pisać ![]() , co czytamy
jako
, co czytamy
jako ![]() jest preferowane przed
jest preferowane przed ![]() ,
, ![]() jest niegorsze
niż
jest niegorsze
niż ![]() albo
albo ![]() jest przynajmniej tak samo dobre jak
jest przynajmniej tak samo dobre jak ![]() . Analogicznie piszemy
. Analogicznie piszemy ![]() i czytamy
i czytamy ![]() jest
ściśle preferowane przed
jest
ściśle preferowane przed ![]() ,
, ![]() jest lepszy niż
jest lepszy niż ![]() albo agent woli
albo agent woli ![]() niż
niż ![]() . Podobnie dla relacji obojętności (niektórzy ekonomiści używają karkołomnej kalki
z języka angielskiego indyferencja) piszemy
. Podobnie dla relacji obojętności (niektórzy ekonomiści używają karkołomnej kalki
z języka angielskiego indyferencja) piszemy ![]() i czytamy
i czytamy ![]() jest tak samo dobry jak
jest tak samo dobry jak ![]() albo agentowi jest wszystko
jedno, czy wybrać
albo agentowi jest wszystko
jedno, czy wybrać ![]() czy
czy ![]() (jeżeli usłyszymy agent jest indyferentny pomiędzy
(jeżeli usłyszymy agent jest indyferentny pomiędzy ![]() a
a ![]() , to mówiącemu właśnie o to chodzi).
, to mówiącemu właśnie o to chodzi).
Agent musi wybrać element zbioru budżetowego ![]() ,
który maksymalizuje relację preferencji: optymalnym wyborem są
takie
,
który maksymalizuje relację preferencji: optymalnym wyborem są
takie ![]() , że dla każdego
, że dla każdego ![]() zachodzi
zachodzi ![]() .
.
Kluczowym założeniem w teorii ekonomii jest to, że podejmujący decyjzę jest racjonalny. Każdy chętnie zgodzi się z tym założeniem, chociaż nie każdy potrafiłby je formalnie zdefiniować. Warunki na racjonalność mogą być różne, ale dwa z nich są bezdyskusyjne: (1) jeżeli mam do wyboru dwie możliwości, to potrafię je porównać (tzn. powiedzieć, która z nich jest lepsza albo że obie są tak samo dobre); (2) jeśli mam trzy możliwości, z których pierwsza jest niegorsza niż druga, a druga niegorsza niż trzecia, to pierwsza powinna być niegorsza niż trzecia.
Matematycznie te dwa warunki mają oczywistą postać:
Definicja 1.2
Relacja ![]() jest racjonalna, jeśli jest ona zupełna
(spójna) i przechodnia.
jest racjonalna, jeśli jest ona zupełna
(spójna) i przechodnia.
Dlaczego racjonalność jest tak istotna?
Przykład 1.2
Skutki braku racjonalności
W stołówce studenckiej mamy do wyboru trzy zupy: pomidorową,
ogórkową i krupnik (![]() ).
).
a) Brak zupełności
Jaś ma relację preferencji ![]() . Nie wie, czy wolałby
krupnik, czy ogórkową, czy jest mu to obojętne. Jeśli
podejmie jakąś decyzję, może wybrać gorszą
możliwość. Jeśli nie dookreśli swoich preferencji, to
minie przerwa i Jaś głodny pójdzie na wykład.
. Nie wie, czy wolałby
krupnik, czy ogórkową, czy jest mu to obojętne. Jeśli
podejmie jakąś decyzję, może wybrać gorszą
możliwość. Jeśli nie dookreśli swoich preferencji, to
minie przerwa i Jaś głodny pójdzie na wykład.
b) Brak przechodniości
Tym razem Jaś ma relację preferencji ![]() .
Kupił już zupę ogórkową. Nie będzie miał nic
przeciwko zamianie jej na krupnik, a nawet zapewne byłby skłonny za to
zapłacić symboliczny grosik. Potem krupnik zamienia na pomidorową,
również za symboliczną dopłatą, a pomidorową na
ogórkową… Koło się zamknęło, wszystkich transakcji
można dokonać ponownie, z czasem uzbiera się z tego spory
kapitał. Wystarczy odkryć brak racjonalności Jasia i możemy na
nim nieźle zarobić.
.
Kupił już zupę ogórkową. Nie będzie miał nic
przeciwko zamianie jej na krupnik, a nawet zapewne byłby skłonny za to
zapłacić symboliczny grosik. Potem krupnik zamienia na pomidorową,
również za symboliczną dopłatą, a pomidorową na
ogórkową… Koło się zamknęło, wszystkich transakcji
można dokonać ponownie, z czasem uzbiera się z tego spory
kapitał. Wystarczy odkryć brak racjonalności Jasia i możemy na
nim nieźle zarobić.
Chociaż założenie racjonalności wydaje się oczywiste, często w rzeczywistych sytuacjach nie jesteśmy racjonalni.
Przykład 1.3
Przykłady braku racjonalności w rzeczywistych sytuacjach
a) Brak zupełności wynikający z niewiedzy
Nie potrafimy porównać rzeczy, na których mało się znamy albo które wymagają zbyt żmudnych obliczeń. We współczesnej ekonomii pojawia się nawet termin ”racjonalna ignorancją”, pod którym kryje się to, że gdy zdobycie pełnej wiedzy potrzebnej do podjęcia decyzji jest znacznie bardziej kosztowne (w porównywalnych jednostkach) niż maksymalna korzyść, jaką dzięki tej wiedzy możemy uzyskać w rozwiązaniu naszego zagadnienia wyboru, to lepiej pozostać w tej kwestii ignorantem.
Zupełność oznacza, coś zupełnie przeciwnego – dokładnie przestudiowaliśmy wszystkie szczegóły i dokładnie wiemy, jakie każdy z nich ma znaczenie.
b) Brak przechodniości wynikający z niedostrzegalnych lub zaniedbywalnych różnic
Jeżeli wybieramy farbę w kolorze kremowym i mamy do wyboru 100 odcieni, to różnice pomiędzy sąsiednimi są niezauważalne, natomiast potrafimy rozróżnić najciemniejszy od najjaśniejszego i określić, który z nich bardziej nam się podoba.
Podobnie, jeżeli przy zakupie samochodu wybieramy lepszą cenę tego samego modelu, to różnica o jeden grosz jest zaniedbywalna. Gdybyśmy jednak porównali cały szereg ofert różniących się o jeden grosz, te zaniedbywalne różnice mogły by zsumować się na już niezaniebdywalną różnicę pomiędzy największą a najmniejszą.
Przechodniość oznacza, że każdy grosz się liczy i nie ma rzeczy nierozróżnialych, jeśli mają różną wartość.
c) Pozorny brak racjonalności wynikający ze zmiany upodobań
Jaś z poprzedniego przykładu w poniedziałek miał apetyt na pomidorową i zdecydowanie wolał ją od innych, a we wtorek na ogórkową.
Racjonalność nie oznacza, że nasze gusty są niezmienne, ale że w momencie podejmowania decyzji bierzemy pod uwagę to, że nasze gusty mogą się zmienić.
Stwierdzenie 1.1
Jeżeli relacja ![]() jest racjonalna, to relacja
jest racjonalna, to relacja ![]() jest relacją równoważności i
jest relacją równoważności i ![]() jest liniowym porządkiem na
jest liniowym porządkiem na
![]() – zbiorze klas abstrakcji
– zbiorze klas abstrakcji ![]() .
.
Udowodnić stwierdzenie.
∎Od tej pory będziemy zawsze zakładać, że podejmujący decyzję jest racjonalny.
Definicja 1.3
Klasy abstrakcji relacji obojętności nazywamy krzywymi obojętności.
Rysunek przedstawiający krzywe obojętności i kierunek ich wzrostu nazywamy mapą obojętności.
Jeżeli jest to możliwe, wygodnie byłoby przyporządkować elementom zbioru wyboru ich wartość dla podejmującego decyzję Wówczas zamiast porównywać pary punktów przy pomocy relacji preferencji, wystarczyłoby znaleźć punkty, w których przyjmowane jest maksimum wartości funkcji użyteczności.
Definicja 1.4
Funkcję ![]() nazywamy funkcją
użyteczności odzwierciedlającą relację preferencji
nazywamy funkcją
użyteczności odzwierciedlającą relację preferencji ![]() , jeśli dla każdego
, jeśli dla każdego ![]() zachodzi
tożsamość
zachodzi
tożsamość ![]() .
.
Jeżeli ![]() jest funkcją użyteczności odzwierciedlającą
jest funkcją użyteczności odzwierciedlającą ![]() , to optymalny wybór ze zbioru
, to optymalny wybór ze zbioru ![]() to zbiór
to zbiór ![]() (zbiór elementów zbioru
(zbiór elementów zbioru ![]() na
których jest przyjmowane maksimum funkcji
na
których jest przyjmowane maksimum funkcji ![]() ).
).
Należy się spodziewać, że jeśli relacja preferencji pozwala na istnienie funkcji użyteczności, to jest racjonalna.
Stwierdzenie 1.2
Jeżeli istnieje funkcja użyteczności odzwierciedlająca relację preferencji ![]() , to
, to ![]() jest racjonalna.
jest racjonalna.
Ćwiczenie 1.7
Udowodnić stwierdzenie.
Okazuje się, że racjonalność jest warunkiem koniecznym, ale nie dostatecznym istnienia funkcji użyteczności.
Twierdzenie 1.1
Niech relacja ![]() będzie racjonalna.
będzie racjonalna.
Wówczas istnieje funkcja użyteczności ![]() odzwierciedlająca
odzwierciedlająca ![]() wtedy i tylko wtedy gdy w zbiorze
wtedy i tylko wtedy gdy w zbiorze ![]() (zbiorze klas abstrakcji relacji obojętności) uporządkowanym
przez relację
(zbiorze klas abstrakcji relacji obojętności) uporządkowanym
przez relację ![]() istnieje zbiór
istnieje zbiór ![]() co najwyżej
przeliczalny i gęsty względem tej relacji.
co najwyżej
przeliczalny i gęsty względem tej relacji.
(![]() ) Wynika, z tego, że przeliczalny podzbiór gęsty
względem relacji
) Wynika, z tego, że przeliczalny podzbiór gęsty
względem relacji ![]() zawsze istnieje w podzbiorach liczb
rzeczywistych. Niech
zawsze istnieje w podzbiorach liczb
rzeczywistych. Niech ![]() – przeliczalny podzbiór gęsty zbioru
– przeliczalny podzbiór gęsty zbioru ![]() . Wówczas
. Wówczas ![]() jest przeliczalny i jest gęsty w zbiorze
jest przeliczalny i jest gęsty w zbiorze ![]() względem
względem ![]() –
jeśli weźmiemy
–
jeśli weźmiemy ![]() , to z
definicji
, to z
definicji ![]()
![]() , a więc z gęstości
, a więc z gęstości ![]() istnieje
istnieje ![]() , takie że
, takie że ![]() , czyli
, czyli ![]() . Ponieważ
. Ponieważ ![]() , mamy gęstość tego zbioru w
, mamy gęstość tego zbioru w ![]() względem
względem ![]() .
.
(![]() ) Niech
) Niech ![]() będzie takim zbiorem co najwyżej
przeliczalny zawierającym elementy największy i najmniejszy
będzie takim zbiorem co najwyżej
przeliczalny zawierającym elementy największy i najmniejszy ![]() względem relacji Ponieważ zbiór
względem relacji Ponieważ zbiór ![]() jest co najwyżej
przeliczalny, ustawiamy jego elementy w ciąg
jest co najwyżej
przeliczalny, ustawiamy jego elementy w ciąg ![]() . Definiujemy
wartości funkcji
. Definiujemy
wartości funkcji ![]() na tym zbiorze rekurencyjnie w następujący
sposób.
na tym zbiorze rekurencyjnie w następujący
sposób.
![]() ,
,
![u(a_{{n}})=\left\{\begin{array}[]{lll}\min _{{k<n}}u(a_{{k}})-\frac{1}{2^{{k}}}&&\text{jeśli }\forall k<n\text{ }a_{{k}}\succ a_{{n}}\text{,}\\
\max _{{k<n}}u(a_{{k}})+\frac{1}{2^{{k}}}&&\text{jeśli }\forall k<n\text{ }a_{{n}}\succ a_{{k}}\text{,}\\
\frac{\min _{{k<n}}u(a_{{k}})+\max _{{k<n}}u(a_{{k}})}{2}&&\text{w przec. przyp.}\end{array}\right.](wyklady/mie/mi/mi64.png)
Jak widać, na zbiorze ![]() funkcja
funkcja ![]() będzie dobrze
odzwierciedlać relację
będzie dobrze
odzwierciedlać relację ![]() .
.
Na pozostałych elementach ![]() definiujemy
definiujemy ![]() jako
jako ![]() . Widać, że
ta definicja jest poprawna i łatwo pokazać, że tak zdefiniowana
funkcja
. Widać, że
ta definicja jest poprawna i łatwo pokazać, że tak zdefiniowana
funkcja ![]() odzwierciedla
odzwierciedla ![]() , czyli
, czyli ![]() .
.
Wystarczy w tym celu pokazać, że
1. ![]() i
i
2. ![]() ,
,
ponieważ 1 i 2 daje nam implikację ![]() , a
, a ![]() to,
ze spójności
to,
ze spójności ![]() negacja
negacja ![]() , co daje nam dowód
nie wprost implikacji
, co daje nam dowód
nie wprost implikacji ![]() (z dokładnością do
przemianowania zmiennych).
(z dokładnością do
przemianowania zmiennych).
2. wynika bezpośrednio z definicji ![]() , a przy dowodzie 1. korzystamy z gęstości
, a przy dowodzie 1. korzystamy z gęstości ![]() . Ponieważ
. Ponieważ ![]() , więc istnieje
, więc istnieje ![]() ,
że
,
że ![]() . Stąd mamy
. Stąd mamy ![]() .
.
Co więcej, co najmniej jedna z tych relacji preferencji musi być
ścisła. Niech zatem ![]() . Z definicji
. Z definicji ![]() wynika, że
wynika, że ![]() , przy czym w
pierwszej nierówności równość może nastąpić
tylko wtedy, gdy oba zbiory są nieskończone, a supremum i infinum
nie jest osiągane na żadnym z elementów
, przy czym w
pierwszej nierówności równość może nastąpić
tylko wtedy, gdy oba zbiory są nieskończone, a supremum i infinum
nie jest osiągane na żadnym z elementów ![]() , natomiast w drugiej
tylko wtedy, gdy
, natomiast w drugiej
tylko wtedy, gdy ![]() . Tak więc co najmniej jedna z tych nierówności jest zawsze ostra, a stąd
. Tak więc co najmniej jedna z tych nierówności jest zawsze ostra, a stąd
![]() .
.
Założenie twierdzenia o istnieniu funkcji użyteczności wydaje się bardzo słabe.
Czy można więc zaryzykować stwierdzenie, że w praktycznych sytuacjach zawsze istnieje funkcja użyteczności, natomiast kontrprzykład jest mało zrozumiałą dla niematematyka teoretyczną konstrukcją?
Nic bardziej mylnego: dla porządku leksykograficznego już w ![]() (zdefiniowanego przez
(zdefiniowanego przez ![]() )
nie istnieje funkcja użyteczności. Porządek leksykograficzny,
wymyślony, zgodnie z nazwą, do porządkowania zawartości słowników, nie jest też zupełnie abstrakcyjny w ekonomii:
)
nie istnieje funkcja użyteczności. Porządek leksykograficzny,
wymyślony, zgodnie z nazwą, do porządkowania zawartości słowników, nie jest też zupełnie abstrakcyjny w ekonomii:
Przykład 1.4
Nieistnienie funkcji użyteczności
Radny Kowalski mieszkający na ulicy Polnej ma zdecydować, jak długi odcinek ulicy Polnej i jaki ulicy Leśnej (na której prawie wcale nie bywa) ma być asfaltowany. Jego relacja preferencji jest oczywista: im większy odcinek ulicy Polnej zostanie pokryty asfaltem, tym lepiej. Jeśli natomiast porównujemy możliwości w których pokryty asfaltem kawałek ulicy Polnej jest taki sam, to im większy kawałek ulicy Leśnej zostanie pokryty, tym lepiej. Preferencje radnego to porządek leksykograficzny, a więc nie istnieje funkcja użyteczności, która je odzwierciedla.
Mamy twierdzenie o istnieniu funkcji użyteczności. Jak jest z jednoznacznością?
Nie tylko nie mamy jednoznaczności, ale nawet fakt zupełnie przeciwny – istnienie nieskończenie wielu funkcji użyteczności odzwierciedlających tę samą relację preferencji.
Stwierdzenie 1.3
(Twierdzenie o monotonicznej transformacji użyteczności)
Jeżeli ![]() jest funkcją użyteczności odzwierciedlającą relację preferencji
jest funkcją użyteczności odzwierciedlającą relację preferencji ![]() , to dla dowolnej funkcji
, to dla dowolnej funkcji ![]() ściśle rosnącej, funkcja
ściśle rosnącej, funkcja ![]() jest
również funkcją użyteczności odzwierciedlającą
jest
również funkcją użyteczności odzwierciedlającą ![]() .
.
Ćwiczenie 1.8
Udowodnić twierdzenie o monotonicznej transformacji użyteczności.
Skoro wybór konkretnej funkcji użyteczności nie ma wpływu na wybór agenta, więc zawsze możemy przyjąć tę funkcję, która ułatwia nam obliczenia.
Ćwiczenie 1.9
Czy relacje preferencji na ![]() opisane werbalnie poniżej są racjonalne? Jeśli tak, narysować mapy obojętności.
opisane werbalnie poniżej są racjonalne? Jeśli tak, narysować mapy obojętności.
Czy istnieje odzwierciedlająca je funkcja użyteczności? Jeśli tak, wypisać.
a) Nasycenie albo błogostan.
Koszyk składający się z dwóch czekoladek i jednej szklanki mleka jest idealny dla Jasia. Jeśli mama podsuwa mu jakikolwiek inny koszyk, to jest on gorszy, przy czym im dalej (euklidesowsko) od idealnego, tym gorzej. Koszyki równie odległe od idealnego są tak samo dobre.
b) Dobra niechciane.
Patryk lubi piwo, ale nie lubi śledzi, jednak każda ilość piwa rekompensuje mu zjedzenie takiej samej ilości śledzi. Poza tym im większy nadmiar piwa nad śledziami, tym lepiej.
c) Z dwóch starających się Ania zawsze woli tego, który jest przystojniejszy i inteligentniejszy.
d) Doskonałe substytuty – stanowią swoje zamienniki w stałym stosunku.
(i) Silnik spala identycznie benzynę i gaz.
(ii) Banknoty 10zł i 20zł.
e) Dobra doskonale komplementarne – konsumowane w stałym stosunku.
(i) Prawe i lewe buty.
(ii) Jacek zawsze pije kawę ze śmietanką zawsze w stosunku 1:2. Im więcej ulubionego napoju, tym lepiej, ale nadmiar któregokolwiek składnika nad idealne proporcje się marnuje.
f) Preferencje Marii Antoniny co do chleba i ciastek definiuje fakt, że ciastka je ona sama (i im więcej tym lepiej), a chleb jest dla ludu (i, jako wielkoduszna królowa, jeśli nie musi ograniczyć swojej konsumpcji, chce, żeby lud był jak najbardziej zadowolony).
g) Na składkowej imprezie jest piwo i wino. Marek chciałby wypić jak najwięcej, nieważne którego z alkoholi, ale nie miesza.




