Zagadnienia

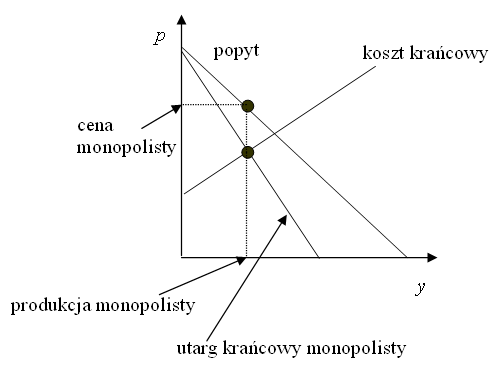
13.1 Monopol a doskonała konkurencja
13.2 Dyskryminacja cenowa

13. Monopol

Jak w modelu równowagi cząstkowej analizujemy rynek pojedynczego towaru, lecz tym razem nie ma konkurencji – jest jej przeciwieństwo. Dla uproszczenia zapisu opuścimy indeks dobra przy cenach i ilościach.

Nazwa pochodzi od prawa wyłącznego handlu. Monopol jest to firma lub mała grupa firm działających wspólnie (a więc bez straty ogólności jedna firma) mająca wyłączność na danym rynku.

Monopol może być naturalny (tak jest np. w przypadu sieci energetycznej), jeśli występują na tyle duże koszty stałe, że nie opłaca się otworzyć drugiej firmy, lub może być spowodowany ograniczeniami wolnej konkurencji. Tak czy inaczej, monopolista działa zawsze na tej samej zasadzie. W odróżnieniu od firmy konkurencyjnej nie jest ”price taker” tylko ”price maker” – to on ustala ceny, ponieważ ustala podaż rynkową, i jest tego świadom. Podobnie jak w równowadze cząstkowej, zakładamy, że monopolista produkuje tylko jeden produkt i maksymalizuje zysk, tym razem jednak cena nie jest stałą daną z zewnątrz.

Maksymalizacja zysku przez monopolistę ma postać: $\max _{{p>0,y\geq 0\\ d(p)\geq y}}py-c(y)$ – jedynym ograniczeniem jest to, żeby ludzie kupili jego produkcję. Oczywiście wystarczy poprzestać na ograniczeniu $d(p)=y$ , gdyż w przeciwnym przypadku monopoliście opłacałoby się podnieść cenę lub wielkość produkcji.

Stąd maksymalizację monopolisty można zapisać równoważnie jako

$\max _{{p>0}}p\cdot d(p)-c(d(p))$

albo

$\max _{{y\geq 0}}p(y)\cdot y-c(y)=\max _{{y\geq 0}}r(y)-c(y)\text{,}$

gdzie $p(y)=d^{{-1}}(y)$ jest odwrotną funkcją popytu, a $r(y)=p(y)\cdot y$ jest to utarg ze sprzedaży. W rzeczywistości warunek $y\geq 0$ można zastąpić $y>0$ , gdyż w przeciwieństwie do firmy wolnokonkurencyjnej monopolista przeważnie ma duże zyski i nie opłaca mu się wstrzymywać produkcji.

Warunek konieczny maksymalizacji zysku ma więc postać $r^{{\prime}}(y)=c^{{\prime}}(y)$ .

Rys. 13.1. Równowaga na rynku z monopolem. Uwaga – osie są na odwrót.

Warunek konieczny $r^{{\prime}}(y)=c^{{\prime}}(y)$ , możemy rozpisać jako $p(y)+p^{{\prime}}(y)\cdot y=c^{{\prime}}(y)$ . Ten prosty zapis ma znów łopatologiczną interpretację ekonomiczną: kiedy monopolista rozważa sprzedaż dodatkowo $dy$ produktu, bierze pod uwagę dwa efekty: po pierwsze zwiększenie przychodu o $p(y)\cdot dy$ przez to, że przy tej samej cenie sprzedaje więcej o $dy$ ; po drugie, aby sprzedać więcej, trzeba zredukować cenę o $dp=\frac{dp}{dy}\cdot dy$ , a więc $y$ jednostek zostanie sprzedane za $p^{{\prime}}(y)\cdot y\cdot dy$ . Razem te dwa efekty dają $p\cdot dy+dp\cdot y=\left(p+\frac{dp}{dy}y\right)dy$ i to musimy przyrównać ze zmianą kosztu produkcji $c^{{\prime}}(y)\cdot dy$ .

Lewą stronę warunku koniecznego można równoważnie zapisać jako 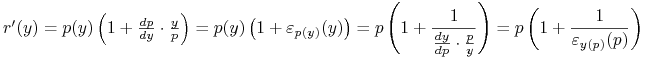$r^{{\prime}}(y)=p(y)\left(1+\frac{dp}{dy}\cdot\frac{y}{p}\right)=p(y)\left(1+\varepsilon _{{p(y)}}(y)\right)=p\left(1+\dfrac{1}{\frac{dy}{dp}\cdot\frac{p}{y}}\right)=p\left(1+\dfrac{1}{\varepsilon _{{y(p)}}(p)}\right)$ , gdzie $\varepsilon _{{y(p)}}(p)$ jest elastycznością cenową popytu przy cenie $p$ , a $\varepsilon _{{p(y)}}(y)$ elastycznością odwrotnej funkcji popytu przy wielkości produkcji $y$ . Powyższe obliczenia możemy podsumować w stwierdzeniu:

Stwierdzenie 13.1

Warunek konieczny maksymalizacji zysku przez monopolistę sprzedającego swój produkt bez różnicowania cen można zapisać równoważnie jako:

a) $r^{{\prime}}(y)=c^{{\prime}}(y)$ (utarg krańcowy równa się kosztowi krańcowemu);

b) $p(y)+p^{{\prime}}(y)\cdot y=c^{{\prime}}(y)$ ;

c) $p(y)\left(1+\varepsilon _{{p(y)}}(y)\right)=c^{{\prime}}(y)$ ;

d) $p\left(1+\dfrac{1}{\varepsilon _{{y(p)}}(p)}\right)=c^{{\prime}}(y(p))$ .

Z warunku d) wynika fakt, że monopolista nigdy nie wybierze ceny, takiej, że popyt przy tej cenie jest nieelastyczny ( $\left|\varepsilon _{{y(p)}}(p)\right|<1$ ): wówczas lewa strona – utarg krańcowy – byłaby ujemna, a prawa jest zawsze dodatnia. Tak więc cena i wielkość produkcji będą takie, że popyt jest przy tej cenie elastyczny. Ekonomicznie jest to oczywiste: nieelastyczny popyt oznacza, że ludzie ”słabo” reagują obniżeniem popytu na zmianę ceny, więc niemalże bezkarnie można cenę podnieść.

13.1. Monopol a doskonała konkurencja

Dla uproszczenia analizy założymy, że koszt produkcji jest liniowy (wówczas tyle samo kosztuje wyprodukowanie tej samej ilości towarów przez $1$ firmę i przez $N$ firm): $c(y)=C\cdot y$ .

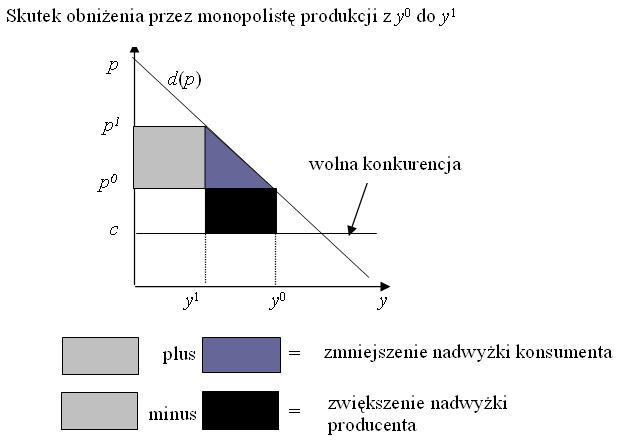
Przy wolnej konkurencji ustali się cena $C$ i ilość dobra na rynku będzie dana równaniem $p(y)=C$ . Natomiast w przypadku monopolu wielkość produkcji to $r^{{\prime}}(y)=C$ , czyli $p(y)+p^{{\prime}}(y)\cdot y=C$ . Ilość produkowana będzie mniejsza niż w przypadku doskonałej konkurencji, a cena wyższa. Podobnie jak w przypadku opodatkowania mamy do czynienia z bezpowrotną stratą spowodowaną zmniejszeniem produkcji: nadwyżka monopolisty jest mniejsza niż to co tracą konsumenci.

Rys. 13.2. Skutki monopolu – bezpowrotna strata z tytułu monopolizacji.

Podobną analizę możemy przeprowadzić dla dowolnej funkcji kosztów jeśli porównamy $N$ firm wolnokonkurencyjnych i monopol posiadający $N$ fabryk o tych samych funkcjach jak w przypadku wolnej konkurencji produkcji i kosztach stałych działalności każdej, co może oznaczać albo faktycznie jednego właściciela, albo tzw. kartel czyli zmowę monopolistyczną pomiędzy $N$ niezależnymi firmami ustalającą ich strategie aby zmaksymalizować łączne zyski.

13.2. Dyskryminacja cenowa

Dyskryminacja cenowa polega na sprzedawaniu różnych jednostek tego samego dobra po różnych cenach (tym samym lub różnym konsumentom). Może być stosowane przy pewnych warunkach przez monopolistę, który chce sprzedać dodatkową jednostkę dobra bez obniżenia ceny sprzedaży dotychczasowych.

Są trzy podstawowe rodzaje dyskryminacji cenowej:

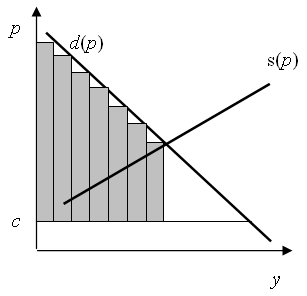
I-ego rodzaju: (doskonała dyskryminacja cenowa) każdemu sprzedajemy każdą jednostkę dobra za maksymalną cenę, jaką jest skłonny za nią zapłacić (tak jakby każda jednostka była sprzedawana na aukcji, przy założeniu, że każdy podaje maksymalną cenę).

W tej sytuacji monopolista zgarnia całą nadwyżkę, a wielkość produkcji jest jak w przypadku wolnej konkurencji i łączna nadwyżka jest taka sama (nie ma więc bezpowrotnej straty – społecznie sytuacja jest lepsza niż brak dyskryminacji). Oczywiście monopolista musi znać strukturę popytu, dlatego jest to sytuacja abstrakcyjna.

Rys. 13.3. Nadwyżka producenta przy dyskryminacji cenowej pierwszego rodzaju.

II-ego rodzaju: (tzw. nieliniowa wycena) cena zależy od liczby zakupionych jednostek dobra (np. obniżka za hurt albo przeciwnie: wyższe opłaty za energię elektryczną po przekroczeniu pewnego pułapu).

Jeżeli konsumenci dzielą się na dwie grupy (lub więcej), jedna z nich ma wyższy popyt przy każdej cenie, a druga niższy i nie można na podstawie innych cech wykryć, kto należy do której grupy. Stąd za małą ilość jest inna cena niż za dużą.

III-ego rodzaju każdy konsument płaci taką samą cenę za każdą jednostkę dobra, ale różnicujemy pomiędzy konsumentami (np. zniżki dla studentów).

Jeżeli konsumenci dzielą się na dwie grupy (lub więcej), jedna z nich ma wyższy popyt przy każdej cenie, a druga niższy i na podstawie innych cech (np. student, emeryt, mieszkaniec określonego miasta) łatwo wykryć, kto należy do której grupy – łatwo ustalić optymalne ceny dla każdej grupy.

Przykład 13.1

W dolinie zagubionej wśród szczytów Himalajów są tylko dwie wioski A i B. Chociaż nie ma administracyjnych ograniczeń konkurencji, ze względu na wysokie koszty transportu alkoholu spoza doliny, w dolinie monopol na sprzedaż alkoholu ma lokalna gorzelnia. Jej funkcja kosztów to $c(y)=y^{{2}}$ . Popyt na alkohol w wiosce A wynosi $d_{{A}}(p)=\left(200-p\right)^{{+}}$ , a w wiosce B $d_{{B}}(p)=\left(300-p\right)^{{+}}$ .

a) Jeśli monopolista może traktować wioski A i B jako oddzielne rynki zbytu (dyskryminacja cenowa trzeciego rodzaju), to jaka będzie cena i ilość konsumowanego alkoholu w każdej z wiosek?

b) Jeśli mieszkańcy są na tyle spostrzegawczy i przedsiębiorczy, że zawsze kupują alkohol tam, gdzie taniej, to jak zmieni się odpowiedź?

c) Pewien przedsiębiorczy Sherpa poinformował sąsiadów, że sam zamierza zacząć pędzić bimber (równie dobry jak produkt gorzelni) i sprzedawać go po cenie 200, bliskiej jego kosztom produkcji. Jak zareaguje monopolista?

a) Mamy tu do czynienia z dyskryminacją cenową trzeciego rodzaju. Maksymalizacja monopolisty ma postać $\max _{{p_{{A}}>0,\ p_{{B}}>0}}d_{{A}}(p_{{A}})\cdot p_{{A}}+d_{{B}}(p_{{B}})\cdot p_{{B}}-c(d_{{A}}(p_{{A}})+d_{{B}}(p_{{B}}))$ albo, równoważnie. $\max _{{y_{{A}}>0,\ y_{{B}}>0}}y_{{A}}\cdot p_{{A}}(y_{{A}})+y_{{B}}\cdot p_{{B}}(y_{{B}})-c(y_{{A}}+y_{{B}})$ , gdzie $p_{{A}}(\cdot)$ i $p_{{B}}(\cdot)$ oznaczają odwrotne funkcje popytu w obu wioskach. Po pracowitych wyliczeniach otrzymujemy $p_{{A}}=183\frac{1}{3}$ , $p_{{B}}=233\frac{1}{3}$ , $y_{{A}}=\frac{50}{3}$ i $y_{{B}}=\frac{200}{3}$ .

b) Monopolista nie może dyskryminować cenowo, więc ustali się wspólna cena wynikająca z maksymalizacji $\max _{{p>0}}(d(p))\cdot p-c(d(p))$ , gdzie $d(p)=d_{{A}}(p)+d_{{B}}(p)$ jest funkcją łącznego popytu; albo, równoważnie, $\max _{{y>0}}y\cdot p(y)-c(y)$ , gdzie $p(\cdot)$ jest funkcją odwrotną do $d$ . W obu przypadkach $y_{{i}}=y_{{i}}(p)$ .

Tu otrzymujemy $p=225$ , a więc $y_{{A}}=0$ . Mieszkańcy wioski $S$ zapewne chcieliby być dyskryminowani cenowo.

c) O ile monopolista nadal będzie miał zysk, a tak jest w tym przypadku, obniży cenę do poziomu, przy którym ewentualnemu konkurentowi nie będzie się opłacało produkować. Wielkość produkcji zależy od popytu – na pewno zwiększy się. Kiedy zagrożenie konkurencją zniknie, monopolista znów podniesie cenę i zmniejszy produkcję.

Ćwiczenie 13.1

Pewien producent zabawek jest monopolistą na rynku opatentowanego przez siebie produktu. Może on produkować dwa rodzaje zabawek – dobrej jakości, pod swoją własną nazwa, i złej jakości, pod nazwą specjalnie w tym celu założonej ”firmy-krzak”. Koszt produkcji każdego rodzaju zabawek jest liniowy, o koszcie krańcowym $5$ dla zabawek niskiej jakości i $6$ dla zabawek wysokiej jakości. Monopolista ponosi też dodatkowo koszt włączenia każdej z linii produkcyjnych w wysokości $\bar{c}$ , do daje funkcję kosztów $c(y_{{w}},y_{{n}})=c_{{w}}(y_{{w}})+c_{{n}}(y_{{n}})$ dla $c_{{w}}=\left\{\begin{array}[]{ll}0&y_{{w}}=0\text{,}\\ \bar{c}+6y_{{w}}&\text{w p.p.}\end{array}\right.$ i $c_{{n}}$ analogicznej. Wiadomo, że kupujący zabawki dzielą się na dwie grupy. Dla pierwszej, nazwijmy ją ”W” zabawki niskiej jakości nie istnieją. Dla drugiej grupy – ”N” – liczy się wojskowa zasada ”sztuka jest sztuka” i jakość kupowanych produktów nie ma znaczenia. Ich popyty określają równania $d_{{w}}(p_{{w}},p_{{n}})=(100-\frac{1}{2}p_{{w}},0)\,$ i $d_{{n}}(p_{{w}},p_{{n}})=\left\{\begin{array}[]{ll}(100-2p_{{w}},0)&p_{{w}}\leq p_{{n}}\text{,}\\ (0,100-2p_{{n}})&\text{w p.p.}\end{array}\right.$

Obie grupy klientów są na pierwszy rzut oka nierozróżnialne.

a) Jak monopolista powinien dyskryminować cenowo, aby zmaksymalizować zysk?

b) Czy przy dyskryminacji możliwe jest, że nie jest produkowany któryś z rodzajów zabawek? Jak to zależy od $\bar{c}$ ? Zakładamy, że jest ono na tyle małe, że przynajmniej jeden rodzaj zabawek opłaca się produkować.

c) Czy przy dyskryminacji możliwe jest, że któraś z grup klientów w ogóle nie będzie kupować?

Jak można przekształcić warunek konieczny z elastycznością popytu, tak, aby można było coś powiedzieć na temat relacji pomiędzy cenami w grupach klientów w przypadku monopolu dyskryminującego cenowo? Przeliczenia analogiczne jak dla przypadku bez dyskryminacji dają nam

$\left\{\begin{array}[]{l}p_{{A}}\left(1+\dfrac{1}{\varepsilon _{{y_{{A}}(p_{{A}})}}(p_{{A}})}\right)=c^{{\prime}}(y_{{A}}(p_{{A}})+y_{{B}}(p_{{B}}))\text{,}\\ p_{{B}}\left(1+\dfrac{1}{\varepsilon _{{y_{{B}}(p_{{B}})}}(p_{{B}})}\right)=c^{{\prime}}(y_{{A}}(p_{{A}})+y_{{B}}(p_{{B}}))\text{.}\end{array}\right.$

Stąd

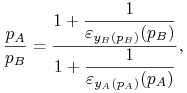$\frac{p_{{A}}}{p_{{B}}}=\frac{1+\dfrac{1}{\varepsilon _{{y_{{B}}(p_{{B}})}}(p_{{B}})}}{1+\dfrac{1}{\varepsilon _{{y_{{A}}(p_{{A}})}}(p_{{A}})}}\text{,}$

czyli klienci z grupy o bardziej elastycznym popycie (o większym module elastyczności) będą płacić taniej niż ci o mniej elastycznym popycie, chyba że z racji zbyt rosnących kosztów krańcowych w ogóle zostaną wykluczeni (to akurat nie może zdarzyć się przy kosztach liniowych).

Ćwiczenie 13.2

Funkcja kosztów monopolisty – jedynego chirurga plastycznego w Powiecie Pskowskim – to $c(y)=90+7\cdot y$ , a odwrotna funkcja popytu na jego produkt $p(y)=\frac{y^{2}}{100}-2\cdot y+100$ .

a) Obliczyć cenę, zysk i poziom produkcji.

b) Zatrudniony przez monopolistę socjolog zauważył, że w dość szerokim przedziale cenowym elastyczność popytu niebieskookich jest dwukrotnie wyższa niż brązowookich. Poszukać możliwości dyskryminacji.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Skrypt do wykładu z mikroekonomii dla wydziału MIMUW 2009/2010