Zagadnienia

14.1 Model czystej wymiany towarowej
14.2 Model Arrowa-Debreu

14. Modele równowagi ogólnej

W przedstawionych tu prostych modelach równowagi ogólnej nie stosujemy sztucznego podziału na odrębne rynki, lecz badamy rynek jako całość. Interesują nas równowagi, jednakże nie analizujemy procesu dochodzenia do równowagi, a jedynie kwestię jej istnienia i własności.

14.1. Model czystej wymiany towarowej

Zaczniemy od analizy sytuacji, w której nie ma producentów – dobra już zostały wyprodukowane i pewne ich koszyki są w posiadaniu konsumentów. Ponieważ jest to w odniesieniu do obecnych rynków sytuacja raczej nietypowa (gracze mają i chcą uzyskać pewne koszyki dóbr, a w tym modelu nie możemy traktować pieniądza jako jednego z dóbr o ustalonej cenie $1$ ), aby łatwiej było o intuicję, wyobraźmy sobie imprezę składkową – każdy z jej uczestników przynosi pewien koszyk dóbr (jeden kiełbaski, drugi chleb i musztardę, trzeci piwo…), po czym każdy chce skonsumować ten koszyk, który jest najlepszy z dostępnych mu – niekoniecznie ten, który przyniósł. Oczywiście im więcej tym lepiej (przynajmniej przy ilościach, które zostały przyniesione).

Mamy $n$ dóbr i skończony zbiór $K$ konsumentów. Zakładamy, że każdy konsument ma zbiór możliwych decyzji $\mathbb{X}=[0,M]^{{n}}$ (gdzie $M$ jest pewną stałą dodatnią), a na nim określoną funkcję użyteczności. Użyteczność $k$ -tego konsumenta będziemy oznaczać przez $u^{{k}}$ . Standartowo będziemy zakładać, że jest ona ciągła, ściśle quasi-wklęsła, monotoniczna i lokalnie nienasycona, jeśli rozszerzymy ją na cały $\mathbb{R}_{{+}}^{{n}}$ .

Na początku $k$ -ty konsument posiada zasób początkowy: koszyk $\omega^{{k}}$ . Konsumenci mogą wymieniać się dobrami, a każdy z nich dąży do tego, żeby mieć jak najwyższą użyteczność.

Definicja 14.1

a) Dowolny wektor koszyków dóbr $\left[x^{{k}}\right]_{{k\in K}}$ , taki że $\sum _{{k\in K}}x^{{k}}\leq\sum _{{k\in K}}\omega^{{k}}$ nazywamy alokacją.

b) Alokację $\left[x^{{k}}\right]_{{k\in K}}$ nazywamy optymalną w sensie Pareto (lub efektywną w sensie Pareto), jeśli nie istnieje inna alokacja $\left[\bar{x}^{{k}}\right]_{{k\in K}}$ , dla której dla każdego $k\in K$ zachodzi nierówność $u^{{k}}(\bar{x}^{{k}})\geq u^{{k}}(x^{{k}})$ i dla co najmniej jednego $k\in K$ zachodzi nierówność $u^{{k}}(\bar{x}^{{k}})>u^{{k}}(x^{{k}})$ .

c) Alokację $\left[x^{{k}}\right]_{{k\in K}}$ nazywamy indywidualnie racjonalną, jeśli dla każdego $k\in K$ zachodzi nierówność $u^{{k}}(x^{{k}})\geq u^{{k}}(\omega^{{k}})$ .

Inaczej mówiąc, alokacja jest takim układem koszyków dóbr, który fizycznie może zostać zrealizowany, jeśli łącznie posiadamy tyle, ile wnieśli uczestnicy wymiany. Często używa się słowa podział, ale wówczas, żeby formalnie był to podział, należałoby umieścić w definicji równość zamiast nierówności. Oczywiście sensowane alokacje są podziałami: chociażby alokacje optymalne w sensie Pareto, a w szczególności równowagi (w dalszych rozważaniach).

Alokacja jest optymalna w sensie Pareto, jeśli nie jest możliwa sytuacja, w której ”polepszamy” przynajmniej jednemu z graczy, a ”nie pogarszamy” żadnemu innemu. Pojęcie optymalności w sensie Pareto ma szerokie zastosowanie we wszelkich zagadnieniach optymalizacji wielokryterialnej, w tym zagadnieniach społecznego wyboru. Pojęcie to jest bardzo słabe – zgodnie z nim nie można porównać ze sobą alokacji, w której jeden z graczy zabiera wszystko, a drugi umiera z głodu, z sytuacją w której bogatszy traci pewną niewielką kwotę na rzecz biedniejszego. Ta słabość porównywania w sensie Pareto jest jeszcze bardziej widoczna w innych zagadnieniach wyboru społecznego – na przykład sytuacji, kiedy złodziej niszczy transformator wart $10000$ złotych, żeby ukraść drut, za który uzyska $100$ złotych (a więc ”globalnie” mamy na minus $9900$ ), nie można porównać z sytaucją, kiedy do kradzieży nie dochodzi. Tak więc gdyby stosować jedynie kryterium Pareto, nie można by było powiedzieć, że kradzież ze zniszczeniem jest dla społeczeństwa gorsza. Ze względu na słabość optymalności w sensie Pareto, jej brak jest zjawiskiem bardzo negatywnym: oznacza, że marnotrawiona jest pewna użyteczność, którą ktoś może uzyskać bez straty użyteczności innych.

Zauważmy, że jeśli wszystkie funkcje użyteczności są ściśle rosnące, to alokacje nie będące podziałami nie są optymalne w sensie Pareto – wówczas można by niewykorzystaną ilość dóbr dać przynajmniej jednemu z graczy.

Alokacja jest indywidualnie racjonalna, jeśli żaden z konsumentów nie będzie wolał swojego zasobu początkowego od proponowanego mu przy tej alokacji koszyka.

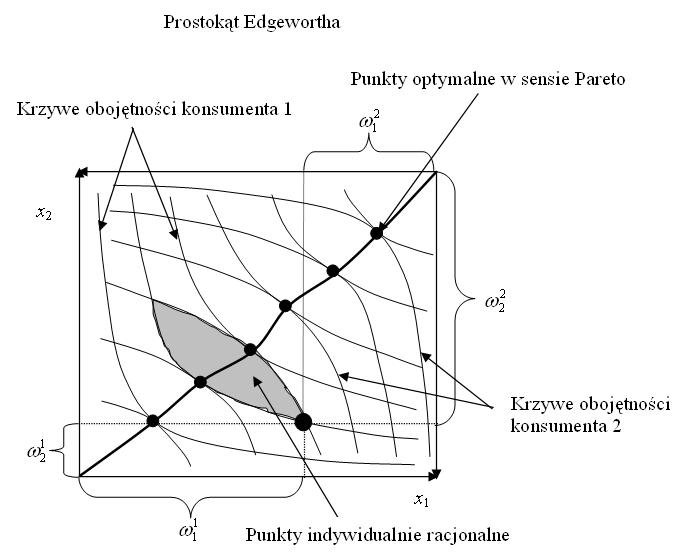
Alokacje będące podziałami przedstawia się na tak zwanym prostokącie Edgewortha (albo też pudełku Edgewortha – Edgeworth box).

Jak rysujemy prostokąt Egdewortha? Najpierw rysujemy mapę obojętności konsumenta $1$ . Następnie na tym samym rysunku umieszczamy drugi układ współrzędnych: o początku w punkcie $(\omega _{{1}}^{{1}}+\omega _{{1}}^{{2}},\omega _{{2}}^{{1}}+\omega _{{2}}^{{2}})$ – sumie zasobów początkowych graczy, czyli ilości dóbr, które mamy do podziału – i obu osiach o zwrotach przeciwnych do analogicznych osi dla konsumenta $1$ . W drugim układzie współrzędnych rysujemy mapę obojętności konsumenta $2$ . Jak łatwo widać, wszystkie punkty prostokątu Edgewortha są podziałami.

Rys. 14.1. Prostokąt Edgewortha.

Optymalność w sensie Pareto i indywidualna racjonalność to minimalne właściwości, jakie powinna mieć alokacja.

Jak widać z rysunku 8.1, przeważnie jest continuum alokacji, które są równocześnie optymalne w sensie Pareto i indywidualnie racjonalne. Tak więc te dwa kryteria nie wystarczają do wyboru alokacji.

Jak więc odbywa się wymiana? Otóż na wszystkie zostają określone ceny. Te ceny nie muszą mieć jakiegokolwiek związku z rzeczywistą wartością dóbr (łyżeczka musztardy może okazać droższa niż kilo kiełbasy i butelka piwa razem wzięte), służą jedynie ustaleniu jednoznacznie alokacji równowagi. Każdy z graczy sprzedaje swój zasób początkowy i za uzyskane pieniądze kupuje taki koszyk, który maksymalizuje jego użyteczność.

Wprawdzie w odniesieniu do imprezy składkowej taki proces wydaje się nieco sztuczny, ale można na niego spojrzeć jako na konstrukcję teoretyczną pozwalającą na wybór jednej alokacji, zwłaszcza jeśli ceny nie będą w pieniądzu, ale na przykład w zapałkach albo specjalnie narysowanych imprezowych banknotach.

Definicja 14.2

Alokację $\left[x^{{k}}\right]_{{k\in K}}$ wraz z wektorem cen $\mathbf{p}$ nazwiemy równowagą Walrasa dla modelu czystej wymiany towarowej, jeśli dla każdego konsumenta jego koszyk przy alokacji jest równy jego popytowi przy tych cenach i dochodzie równym wartości zasobu początkowego $x^{{k}}=x^{{k}}(\mathbf{p},\mathbf{p}^{{T}}\omega^{{k}})$ oraz suma popytów jest nie większa niż suma zasobów początkowych.

Równowaga Walrasa dla modelu czystej wymiany towarowej jest więc to taki wektor koszyków $\left[x^{{k}}\right]_{{k\in K}}$ wraz z wektorem cen $\mathbf{p}$ , że

1) $\forall k\in K$ $\mathbf{p}^{{T}}x^{{k}}\leq\mathbf{p}^{{T}}\omega^{{k}}$ (osiągalność przy cenach $\mathbf{p}$ ),

2) $\forall k\in K$ $\forall\xi\in\mathbb{X}:\mathbf{p}^{{T}}\xi\leq\mathbf{p}^{{T}}\omega^{{k}}$ $\left[u^{{k}}(\xi)\leq u^{{k}}(x^{{k}})\right]$ (optymalność przy cenach $\mathbf{p}$ ) i

3) $\sum _{{k\in K}}x^{{k}}\leq\sum _{{k\in K}}\omega^{{k}}$ (fizyczna dostępność).

Zauważmy, że z definicji nie widać, że równowaga musi być podziałem. Jednak jest nie tylko podziałem, jest również optymalna w sensie Pareto:

Twierdzenie 14.1

(pierwsze twierdzenie Walrasa o dobrobycie)

a) Równowaga Walrasa dla modelu czystej wymiany towarowej jest indywidualnie racjonalna.

b) Jeśli dla każdego $k$ funkcje użyteczności $u^{{k}}$ są monotoniczne i lokalnie nienasycone, to równowaga Walrasa dla modelu czystej wymiany towarowej jest optymalna w sensie Pareto.

Tak więc choć w definicji nie zakładamy, że wszystkie dobra zostają skonsumowane, to równoważnie moglibyśmy to założyć – umieścić równość zamiast nierówności.

Weźmy alokację $\left[x^{{k}}\right]_{{k\in K}}$ , która wraz z wektorem cen $\mathbf{p}$ stanowi równowagę Walrasa.

a) Indywidualna racjonalność:

Przypuśćmy przeciwnie, tzn. istnieje taki konsument $k$ , że $u^{{k}}(x^{{k}})<u^{{k}}(\omega^{{k}})$ . Zauważmy, że zarówno $x^{{k}}$ jak i $\omega^{{k}}$ są dostępne przy cenach $\mathbf{p}$ , a $x^{{k}}$ maksymalizuje $u^{{k}}$ w zbiorze budżetowym $B_{{\mathbf{p},\mathbf{p}^{{T}}\omega^{{k}}}}$ . Tak więc $u^{{k}}(x^{{k}})\geq u^{{k}}(\omega^{{k}})$ – sprzeczność.

b) Optymalność w sensie Pareto:

Przypuśćmy przeciwnie, tzn. istnieje taka alokacja $\left[y^{{k}}\right]_{{k\in K}}$ fizycznie dostępna, że dla każdego konsumenta $k$ $u^{{k}}(y^{{k}})\geq u^{{k}}(x^{{k}})$ i istnieje $l$ , że $u^{{l}}(y^{{l}})>u^{{l}}(x^{{l}})$ . Ponieważ to $x^{{l}}$ a nie $y^{{l}}$ został wybrany, $y^{{l}}$ nie mogło być dostępne przy cenach, czyli $\mathbf{p}^{{T}}y^{{l}}>\mathbf{p}^{{T}}\omega^{{l}}$ . Ponieważ funkcja $u$ jest monotoniczna i lokalnie nienasycona, więc spełnia prawo Walrasa. Tak więc dla każdego $k$ $y^{{k}}$ nie może należeć do wnętrza $B_{{\mathbf{p},\mathbf{p}^{{T}}\omega^{{k}}}}$ , czyli $\mathbf{p}^{{T}}y^{{k}}\geq\mathbf{p}^{{T}}\omega^{{k}}$ (z przynajmniej jedną nierównością ostrą, co przed chwilą pokazaliśmy).

Jeżeli zsumujemy te wszystkie nierówności po $k$ , otrzymamy $\sum _{{k\in K}}\mathbf{p}^{{T}}y^{{k}}>\sum _{{k\in K}}\mathbf{p}^{{T}}\omega^{{k}}$ .

Natomiast gdy przemożymy nierówność fizycznej dostępności obustronnie przez $\mathbf{p}$ , otrzymamy $\sum _{{k\in K}}\mathbf{p}^{{T}}y^{{k}}\leq\sum _{{k\in K}}\mathbf{p}^{{T}}\omega^{{k}}$ – sprzeczność.

∎

Kolejnym pytaniem jest, czy dowolny koszyk optymalny w sensie Pareto i indywidualnie racjonalny można uzyskać dobierając odpowiednie ceny. I tu odpowiedź jest również twierdząca.

Twierdzenie 14.2

(drugie twierdzenie Walrasa o dobrobycie)

Przy założeniach modelu jeśli alokacja $\left[x^{{k}}\right]_{{k\in K}}$ jest optymalna w sensie Pareto, to istnieje taki układ zasobów początkowych konsumentów $[\omega^{{k}}]_{{k\in K}}$ oraz wektor cen $\mathbf{p}$ , że $\left[x^{{k}}\right]_{{k\in K}}$ z $\mathbf{p}$ stanowi równowagę Walrasa dla modelu czystej wymiany towarowej przy układzie zasobów początkowych konsumentów $[\omega^{{k}}]_{{k\in K}}$ .

Dla dwóch konsumentów – wszystko to będziemy rozważać na prostokącie Edgewortha, gdzie zbiory związane z $k$ -tym konsumentem zaznaczamy w jego układzie współrzędnych. Będziemy korzystać z twierdzenia o hiperpłaszczyźnie rozdzielającej. Ponieważ $\left[x^{{k}}\right]_{{k\in K}}$ – optymalny w sensie Pareto, więc stanowi on ”punkt styczności” dwóch zbiorów $\{ x\in\mathbb{R}_{{+}}^{{n}}:u^{{k}}(x)\geq u^{{k}}(x^{{k}})\}$ w prostokącie Edgewortha – należy do brzegu obu. Ponieważ $u^{{k}}$ – quasi-wklęsłe, te zbiory są wypukłe. Rozdzielamy wnętrza tych zbiorów – dwa zbiory wypukłe rozłączne. Z jednego z twierdzeń o hiperpłaszczyźnie rozdzielającej dwa zbiory wypukłe rozłączne $A$ i $B\in\mathbb{R}^{{n}}$ istnieje wektor $\mathbf{p}\in\mathbb{R}^{{n}}$ , że dla każdego $x\in A$ i $y\in B$ $\mathbf{p}^{{T}}x\leq\mathbf{p}^{{T}}y$ . W naszym przypadku $A$ i $B$ to zbiory $\{ x\in\mathbb{R}_{{+}}^{{n}}:u^{{k}}(x)\geq u^{{k}}(x^{{k}})\}$ dla obu graczy w prostokącie Edgewortha. Ten wektor $\mathbf{p}$ ma wszystkie współrzędne nieujemne, gdyż $\{ x\in\mathbb{R}_{{+}}^{{n}}:u^{{k}}(x)\geq u^{{k}}(x^{{k}})\}$ zawiera $\{ x\in\mathbb{R}_{{+}}^{{n}}:x\geq x^{{k}}\}$ , tak więc jest naszym wektorem cen równowagi przy dowolnym $[\omega^{{k}}]_{{k\in K}}$ należącego do prostej rozdzielającej.

∎

Kolejne naturalne pytanie, to czy równowaga istnieje. Odpowiedź jest również twierdząca, lecz odpowiednie twierdzenie sformułujemy dla znacznie ogólniejszego modelu – modelu Arrowa-Debreu, w którym oprócz konsumentów mamy również producentów.

Ćwiczenie 14.1

Na bezludnej wyspie mieszkają tylko Robinson i Piętaszek. Robinson ma 10 orzechów kokosowych i dwie ryby, a Piętaszek 5 ryb i jeden orzech. Ich funkcje użyteczności to, odpowiednio $min(o,r)$ i $o\cdot r^{2}$ . Naszkicować prostokąt Edgewortha i zaznaczyć na nim podziały indywidualnie racjonalne i podziały optymalne w sensie Pareto. Obliczyć równowagę Walrasa jeśli jest lub udowodnić, że jej nie ma.

Ćwiczenie 14.2

Bliźniaczki Joasia i Kasia dostały w prezencie od szalonego wujka buty – jednakowe poza jedną cechą: Joasia dostała 3 buty prawe, a Kasia 4 lewe.

Preferencje dziewczynek co do butów są naturalne – im więcej par, tym lepiej.

Czy w modelu istnieje równowaga Walrasa? Jeśli tak, obliczyć.

14.2. Model Arrowa-Debreu

Założenia o konsumentach w modelu Arrowa-Debreu są takie same jak w modelu czystej wymiany towarowej.

Ponadto mamy skończony zbiór $F$ firm.

Każdy konsument może posiadać akcje firm. Liczbę akcji $f$ -tej firmy w rękach $k$ -tego konsumenta będziemy oznaczać przez $T_{{f}}^{{k}}$ . Akcja oznacza udział w zysku (czyli także udział w stracie, jeśli firma przynosi stratę). Tak więc zakładamy, że $\sum _{{k\in K}}T_{{f}}^{{k}}=1$ .

Firma $f$ ma zbiór dostępnych technologii $\mathbb{Y}^{{f}}\subset\left[-M,M\right]^{{n}}$ . Wszystkie $\mathbb{Y}^{{f}}$ są niepuste, domknięte i ściśle wypukłe. Każda z firm maksymalizuje zysk, traktując ceny jako dane, przy czym kupuje czynniki produkcji od konsumentów i sprzedaje im produkty.

Definicja 14.3

Równowagą Walrasa nazywamy układ wektorów $\left[x^{{k}}\right]_{{k\in K}}$ , $\left[y^{{f}}\right]_{{f\in F}}$ wraz z wektorem cen $\mathbf{p}$ , taki że

1) $\forall f\in F$ $\forall y^{{f}}\in\mathbb{Y}^{{f}}$ (wykonalność planów produkcyjnych);

2) $\forall k\in K$ $\mathbf{p}^{{T}}x^{{k}}\leq\mathbf{p}^{{T}}\omega^{{k}}+\sum _{{f\in F}}T_{{f}}^{{k}}\cdot\mathbf{p}^{{T}}y^{{f}}$ (osiągalność planów konsumpcyjnych przy cenach $\mathbf{p}$ );

3) $\forall f\in F$ $\forall\theta\in\mathbb{Y}^{{f}}$ $\left[\mathbf{p}^{{T}}\theta\leq\mathbf{p}^{{T}}y^{{f}}\right]$ (maksymalizacja zysku przez producentów);

4) $\forall k\in K$ $\forall\xi\in\mathbb{X}:\mathbf{p}^{{T}}\xi\leq\mathbf{p}^{{T}}\omega^{{k}}+\sum _{{f\in F}}T_{{f}}^{{k}}\cdot\mathbf{p}^{{T}}y^{{f}}$ $\left[u^{{k}}(\xi)\leq u^{{k}}(x^{{k}})\right]$ (maksymalizacja użyteczności przez konsumentów);

5) $\sum _{{k\in K}}x^{{k}}\leq\sum _{{k\in K}}\omega^{{k}}+\sum _{{f\in F}}^{{k}}y^{{f}}$ (fizyczna dostępność planów konsumpcyjnych), przy czym jeśli po $i$ -tej współrzędnej nierówność jest ostra, to $p_{{i}}=0$ .

Twierdzenie 14.3

Przy założeniach modelu istnieje równowaga Walrasa.

Niech $y^{{f}}(\mathbf{p})$ oznacza plan produkcyjny maksymalizujący zysk producenta $f$ przy cenie $\mathbf{p}$ , a $x^{{k}}(\mathbf{p})$ – koszyk maksymalizujący użyteczność konsumenta $k$ wśród osiągalnych przy $\mathbf{p}$ planów konsumpcyjnych, przy założeniu że producenci wybierają swoje $y^{{f}}(\mathbf{p})$ .

Z twierdzenia o maksimum $y^{{f}}$ jest ciągłą funkcją zmiennej $\mathbf{p}$ . Z powyższego faktu i z twierdzenia o maksimum, również $x^{{k}}$ jest ciągłą funkcją zmiennej $\mathbf{p}$ .

Konstruujemy funkcję nadwyżki popytu $z(\mathbf{p})=\sum _{{k\in K}}x^{{k}}(\mathbf{p})-(\sum _{{k\in K}}\omega^{{k}}+\sum _{{f\in F}}y^{{f}}(\mathbf{p}))$ (ujemne wartości oznaczają nadwyżkę podaży).

Z prawa Walrasa dla optymalizacji konsumenta otrzymujemy, że dla każdego $k$ $\mathbf{p}^{{T}}x^{{k}}(\mathbf{p})-\left(\mathbf{p}^{{T}}\omega^{{k}}+\sum _{{f\in F}}T_{{f}}^{{k}}\cdot\mathbf{p}^{{T}}y^{{f}}(\mathbf{p})\right)=0$ .

Twierdzenie 14.4 (Prawo Walrasa (dla rynku))

Przy założeniach modelu dla każdego wektora cen $\mathbf{p}$ $\mathbf{p}^{{T}}z(\mathbf{p})=0$ (nadwyżka popytu jest prostopadła do $\mathbf{p}$ ).

Ekonomiści formułują to jako ”wartość niedoborów jest równa wartości nadwyżek”.

(prawa Walrasa dla rynku)

Jeśli dodamy równości wynikające z prawa Walrasa dla konsumentów, otrzymamy $0=\sum _{{k\in K}}\left(\mathbf{p}^{{T}}x^{{k}}(\mathbf{p})-(\mathbf{p}^{{T}}\omega^{{k}}+\sum _{{f\in F}}T_{{f}}^{{k}}\mathbf{p}^{{T}}y^{{f}}(\mathbf{p})\right)=$ $=\sum _{{k\in K}}\mathbf{p}^{{T}}x^{{k}}(\mathbf{p})-\sum _{{k\in K}}\mathbf{p}^{{T}}\omega^{{k}}-\sum _{{f\in F}}\sum _{{k\in K}}T_{{f}}^{{k}}\mathbf{p}^{{T}}y^{{f}}(\mathbf{p})=$ (ponieważ udziały sumują się do $1$ ) $=\sum _{{k\in K}}\mathbf{p}^{{T}}x^{{k}}(\mathbf{p})-\sum _{{k\in K}}\mathbf{p}^{{T}}\omega^{{k}}-\sum _{{f\in F}}\mathbf{p}^{{T}}y^{{f}}(\mathbf{p})=$ $=\mathbf{p}^{{T}}\left(\sum _{{k\in K}}x^{{k}}(\mathbf{p})-\sum _{{k\in K}}\omega^{{k}}-\sum _{{f\in F}}y^{{f}}(\mathbf{p}\right)=\mathbf{p}^{{T}}z(\mathbf{p})$ .

∎

Wracamy do dowodu twierdzenia o istnieniu równowagi.

Twierdzenie to można równoważnie sformułować: istnieje cena, dla której nadwyżka popytu jest równa $0$ . Ponieważ na pewno nie jest to wektor $\mathbf{0}$ , a zarówno $x^{{k}}$ jak i $y^{{f}}$ są jednorodne stopnia $0$ , możemy ograniczyć się do wektorów cen, których współrzędne sumują się do $1$ – sympleksu $\Delta=\{\mathbf{p}\in\mathbb{R}_{{+}}^{{n}}:\sum _{{i=1}}^{{n}}p_{{i}}=1\}$ .

Ustalam dowolny wektor cen $\mathbf{p}$ . Przy tych cenach mogą wystąpić niedobory – w konstrukcji nowej ceny $f(\mathbf{p})$ rozpatrywać tylko faktyczne nadwyżki, zaniedbując niedobory. Wprowadzamy oznaczenie: dla $\xi\in\mathbb{R}^{{n}}$ oznaczmy przez $\xi^{{+}}$ wektor $\max\{ 0,\xi\}$ .

Na sympleksie $\Delta$ definiujemy funkcję $f(\mathbf{p})=\frac{\mathbf{p}+\left(z(\mathbf{p})\right)^{{+}}}{\left\|\mathbf{p}+\left(z(\mathbf{p})\right)^{{+}}\right\| _{{1}}}=\frac{\mathbf{p}+\left(z(\mathbf{p})\right)^{{+}}}{1+\sum _{{i=1}}^{{n}}\left(z_{{i}}(\mathbf{p})\right)^{{+}}}$ .

Funkcja $f:\Delta\rightarrow\Delta$ i jest ciągła, a więc na mocy twierdzenia Brouwera istnieje $\mathbf{p}\in\Delta$ takie, że $f(\mathbf{p})=\mathbf{p}$ .

Czyli dla każdego $i$ $\frac{p_{{i}}+\left(z(\mathbf{p})\right)_{{i}}^{{+}}}{1+\sum _{{j=1}}^{{n}}\left(z_{{j}}(\mathbf{p})\right)^{{+}}}=p_{{i}}$ . Stąd $p_{{i}}+\left(z(\mathbf{p})\right)_{{i}}^{{+}}=p_{{i}}\cdot\left(1+\sum _{{j=1}}^{{n}}\left(z_{{j}}(\mathbf{p})\right)^{{+}}\right)$ , czyli $p_{{i}}+\left(z(\mathbf{p})\right)_{{i}}^{{+}}=p_{{i}}+p_{{i}}\sum _{{j=1}}^{{n}}\left(z_{{j}}(\mathbf{p})\right)^{{+}}$ , $\left(z(\mathbf{p})\right)_{{i}}^{{+}}=p_{{i}}\sum _{{j=1}}^{{n}}\left(z_{{j}}(\mathbf{p})\right)^{{+}}|\cdot z_{{i}}(\mathbf{p})$ $z_{{i}}(\mathbf{p})\cdot\left(z_{{i}}(\mathbf{p})\right)^{{+}}=z_{{i}}(\mathbf{p})\cdot p_{{i}}\cdot\sum _{{j=1}}^{{n}}\left(z_{{j}}(\mathbf{p})\right)^{{+}}$ , co sumujemy po $i$ i otrzymujemy: $\sum _{{i=1}}^{{n}}z_{{i}}(\mathbf{p})\cdot\left(z_{{i}}(\mathbf{p})\right)^{{+}}=\sum _{{i=1}}^{{n}}\left(z_{{i}}(\mathbf{p})\cdot p_{{i}}\cdot\sum _{{j=1}}^{{n}}\left(z_{{j}}(\mathbf{p})\right)^{{+}}\right)$ , a więc $\sum _{{i=1}}^{{n}}z_{{i}}(\mathbf{p})\cdot\left(z_{{i}}(\mathbf{p})\right)^{{+}}=\sum _{{i=1}}^{{n}}\left(z_{{i}}(\mathbf{p})\cdot p_{{i}}\right)\cdot\sum _{{j=1}}^{{n}}\left(z_{{j}}(\mathbf{p})\right)^{{+}}$ Z prawa Walrasa dla rynku $\sum _{{i=1}}^{{n}}\left(z_{{i}}(\mathbf{p})\cdot p_{{i}}\right)=0$ , a więc $\sum _{{i=1}}^{{n}}z_{{i}}(\mathbf{p})\cdot\left(z_{{i}}(\mathbf{p})\right)^{{+}}=0$ , czyli nie ma faktycznych nadwyżek popytu– mogą być tylko niedobory. Tak więc $\sum _{{k\in K}}x^{{k}}\leq\sum _{{k\in K}}\omega^{{k}}+\sum _{{f\in F}}y^{{f}}$ – brakujący warunek 5. równowagi Walrasa (reszta była automatycznie spełniona).

∎

Twierdzenie o istnieniu udowodniliśmy przy bardzo silnych założeniach. Gdybyśmy nie zakładali ścisłej a tylko zwykłą quasi-wklęsłość funkcji użyteczności lub wypukłość zbiorów dostępnych technologii, nie ma wówczas jednoznaczności – popyt lub podaż nie jest funkcją, lecz odwzorowaniem wielowartościowym. Twierdzenie o istnieniu równowagi Walrasa pozostaje prawdziwe, lecz dowód staje się bardziej skomplikowany, jednak wszystko się przenosi: zamiast funkcji popytu i podaży mamy odwzorowania wielowartościowe, zamiast ciągłości funkcji – półciągłość górną odzworowań wielowartościowych, a twierdzenie Brouwera trzeba zastąpić twierdzeniem Kakutaniego o istnieniu punktu stałego dla odwzorowania wielowartościowego.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Skrypt do wykładu z mikroekonomii dla wydziału MIMUW 2009/2010