2. Podstawy teorii oprocentowania
Treść tego rozdziału jest punktem wyjścia dla samodzielnej dyscypliny
zwanej często matematyką finansową.
Podamy tutaj niezbędne w dalszym ciągu wykładu podstawowe wiadomości
, natomiast pełniejsze opracowanie omawianych zagadnień można znaleźć
w [6] lub [1]. Załóżmy , że inwestujemy dzisiaj kwotę
![]() , która po roku wzrasta do
, która po roku wzrasta do ![]() (zdarza się, że
(zdarza się, że ![]() –
wtedy wzrost jest ujemny). Liczbę
–
wtedy wzrost jest ujemny). Liczbę ![]() określoną wzorem
określoną wzorem
| (2.1) |
nazywamy stopą zwrotu z tej inwestycji. Po przekształceniu wzoru (2.1) otrzymujemy
| (2.2) |
Liczbę ![]() nazywamy czynnikiem akumulującym. W ciągu roku
u różnych podmiotów gospodarczych zrealizują się, oczywiście, różne
stopy zwrotu. W celu uporządkowania i uproszczenia dalszych rozważań
przyjmujemy, że dominująca stopa zwrotu na przestrzeni
kilku okresów, jest równa
nazywamy czynnikiem akumulującym. W ciągu roku
u różnych podmiotów gospodarczych zrealizują się, oczywiście, różne
stopy zwrotu. W celu uporządkowania i uproszczenia dalszych rozważań
przyjmujemy, że dominująca stopa zwrotu na przestrzeni
kilku okresów, jest równa ![]() . Będziemy ją nazywać
efektywną stopą procentową.
. Będziemy ją nazywać
efektywną stopą procentową.
Jeśli więc dziś założę lokatę bankową w wysokości ![]() , to
po roku otrzymam
, to
po roku otrzymam
Jeśli jednak nie podejmę tych pieniędzy, ale przedłużę lokatę na rok następny, to na koniec drugiego roku trwania lokaty otrzymam
Kapitał rośnie zatem tak jak ciąg geometryczny, po ![]() latach
będę miał w banku
latach
będę miał w banku
Kwotę ![]() , która przyrosła w
, która przyrosła w ![]() -tym roku, nazywamy bieżącymi
odsetkami; wynosi ona
-tym roku, nazywamy bieżącymi
odsetkami; wynosi ona
Spójrzmy teraz na rozważany problem z innej strony. Chcę dysponować
kapitałem
![]() za rok od dziś. Ile powinienem teraz zainwestować (
za rok od dziś. Ile powinienem teraz zainwestować (![]() ?), jeśli
efektywna stopa procentowa wynosi
?), jeśli
efektywna stopa procentowa wynosi ![]() ? Odpowiedź uzyskujemy przekształcając
wzór (2.2)
? Odpowiedź uzyskujemy przekształcając
wzór (2.2)
| (2.3) |
Liczbę
| (2.4) |
nazywamy czynnikiem dyskontującym. Poglądowo można powiedzieć, że a kumuluje on wstecz (rys.1). Wzór (2.3) zapiszemy teraz w postaci bardziej przypominającej (2.2)
| (2.5) |
Liczbę ![]() występującą w tej zależności nazywamy
efektywną stopą dyskontową.
Ze wzorów (2.3),(2.4) i (2.5) wynika, że
występującą w tej zależności nazywamy
efektywną stopą dyskontową.
Ze wzorów (2.3),(2.4) i (2.5) wynika, że
| (2.6) |
Liczba ![]() jest miarą odsetek pobieranych z góry. Jeśli
więc pożyczamy od kogoś
jest miarą odsetek pobieranych z góry. Jeśli
więc pożyczamy od kogoś ![]() zł z efektywną stopą dyskonta
zł z efektywną stopą dyskonta ![]() ,
to dostajemy tylko
,
to dostajemy tylko ![]() zł, a po roku oddajemy kapitał
zł, a po roku oddajemy kapitał ![]() zł.
Pożyczkodawca osiągnął
więc stopę zwrotu
zł.
Pożyczkodawca osiągnął
więc stopę zwrotu
Taką samą stopę zwrotu osiągnąłby pobierając odsetki po roku,
w wysokości ![]() zł.
zł.
Równanie typu
| (2.7) |
nazywamy równaniem wartości. Jeśli trzy spośród czterech liczb
![]() są dane, to czwartą można obliczyć z tego równania.
Jeśli niewiadomą jest czas inwestycji
są dane, to czwartą można obliczyć z tego równania.
Jeśli niewiadomą jest czas inwestycji ![]() , to z równania (2.7)
otrzymuje się na ogół
niecałkowitą wartość
, to z równania (2.7)
otrzymuje się na ogół
niecałkowitą wartość ![]() (najczęściej niewymierną).
Dlatego wprowadza się
tzw. kapitalizację ciągłą. Wyjaśnimy krótko jej sens.
(najczęściej niewymierną).
Dlatego wprowadza się
tzw. kapitalizację ciągłą. Wyjaśnimy krótko jej sens.
Niech ![]() będzie dowolną liczbą dodatnią (np.
będzie dowolną liczbą dodatnią (np. ![]() ).
Chcę pobrać z banku początkowy depozyt
).
Chcę pobrać z banku początkowy depozyt ![]() po czasie
po czasie ![]() .
Bank wypłaca mi
.
Bank wypłaca mi
Odsetki były tu naliczane cały czas ( w sposób ciągły), a nie tylko dopisywane na koniec roku.
2.1. Nominalne stopy oprocentowania i dyskonta.Intensywność oprocentowania
Bank w którym mam swój ROR, kapitalizuje moje saldo (tzn. dopisuje
odsetki) co miesiąc, nominalna stopa oprocentowania wynosi
![]() . Co to znaczy w praktyce? Oznacza to , że po miesiącu stan
mojego konta wyniesie
. Co to znaczy w praktyce? Oznacza to , że po miesiącu stan
mojego konta wyniesie
a po ![]() miesiącach
miesiącach
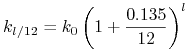 |
(zakładamy , że w międzyczasie nic nie wpłacam i nic nie podejmuję); na przykład po roku mam na koncie
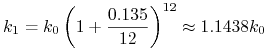 |
Powyższe rozważania streszczamy krótko:
Nominalnej stopie![]() odpowiada efektywna stopa
(roczna)
odpowiada efektywna stopa
(roczna)![]() .
.
Ogólnie, jeśli dopisywanie odsetek odbywa się ![]() razy w ciągu roku
(oczywiście
razy w ciągu roku
(oczywiście ![]() jest całkowite!), to nominalna stopa
jest całkowite!), to nominalna stopa ![]() jest powiązana z równoważną jej stopą efektywną
jest powiązana z równoważną jej stopą efektywną ![]() zależnością
zależnością
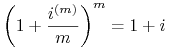 |
(2.8) |
Po roku musi przyrosnąć taka sam kwota po obu stronach w zależności
(2.8), chociaż po
lewej przyrasta ![]() razy, a po prawej tylko raz. Rozumowanie takie można
powtórzyć dla nominalnych stóp dyskontowych; otrzymuje się
wówczas zależność
razy, a po prawej tylko raz. Rozumowanie takie można
powtórzyć dla nominalnych stóp dyskontowych; otrzymuje się
wówczas zależność
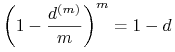 |
(2.9) |
W tym kontekście ciekawe uzasadnienie można podać dla kapitalizacji ciągłej.
Załóżmy, że w naszym mieście jest nieskończenie wiele banków .
Każdy z nich oferuje taką samą nominalną stopę oprocentowania
![]() rachunków
ROR, z tym że w banku nr
rachunków
ROR, z tym że w banku nr ![]() odsetki są kapitalizowane
odsetki są kapitalizowane ![]() razy
w ciągu roku – np. bank nr 365 dopisuje odsetki codziennie.
Niech teraz
razy
w ciągu roku – np. bank nr 365 dopisuje odsetki codziennie.
Niech teraz ![]() oznacza efektywną roczną stopę oprocentowania,
którą uzyskamy w banku nr
oznacza efektywną roczną stopę oprocentowania,
którą uzyskamy w banku nr ![]() . Mamy więc
. Mamy więc
Ponieważ liczby te wzrastają wraz z ![]() , więc im większy jest
numer banku,
tym korzystniejsza jest jego oferta. Czy można przebić tę nieskończoną
mnogość coraz lepszych ofert? Okazuje się , że tak! Ponieważ
, więc im większy jest
numer banku,
tym korzystniejsza jest jego oferta. Czy można przebić tę nieskończoną
mnogość coraz lepszych ofert? Okazuje się , że tak! Ponieważ
| (2.10) |
więc wystarczy założyć bank (nazwijmy go umownie bankiem granicznym) i zaproponować efektywną roczną stopę oprocentowania w wysokości
| (2.11) |
Odsetki wypłaca się raz do roku w powyższej wysokości.
Co to ma wspólnego z kapitalizacją ciągłą? Załóżmy, że
chcemy wycofać pieniądze w chwili ![]() , gdzie
o
, gdzie
o ![]() nic się nie zakłada. Dla większości banków
nic się nie zakłada. Dla większości banków ![]() nie będzie
całkowitą wielokrotnością ich okresu odsetkowego (
nie będzie
całkowitą wielokrotnością ich okresu odsetkowego (![]() roku), ale
załóżmy, że taki bank zaliczy nam łaskawie ostatnią cząstkę
okresu odsetkowego jako cały. Nasz początkowy kapitał
roku), ale
załóżmy, że taki bank zaliczy nam łaskawie ostatnią cząstkę
okresu odsetkowego jako cały. Nasz początkowy kapitał ![]() wzrośnie więc
po czasie
wzrośnie więc
po czasie ![]() w banku nr
w banku nr ![]() do
do
![k(m)=k_{0}\left(1+\frac{\delta}{m}\right)^{{[tm]+1}}](wyklady/muz/mi/mi22.png) |
(![]() oznacza część całkowitą liczby
oznacza część całkowitą liczby ![]() ). Otrzymujemy stąd
). Otrzymujemy stąd
![\lim _{{m\rightarrow\infty}}k(m)=k_{0}\lim _{{m\rightarrow\infty}}\left(\left(1+\frac{\delta}{m}\right)^{m}\right)^{{\frac{[tm]+1}{m}}}=k_{0}e^{{\delta t}}=k_{0}(1+i)^{t}](wyklady/muz/mi/mi11.png) |
Skorzystaliśmy z (2.10) i (2.11). Wobec tego nasz bank
graniczny
w chwili ![]() powinien wypłacić
powinien wypłacić
tzn. powinien kapitalizować odsetki w sposób ciągły. Liczbę
| (2.12) |
nazywamy intensywnością oprocentowania. łatwo pokazać, że
gdzie ![]() ,
, ![]() są stopami nominalnymi równoważnymi
zadanej efektywnej stopie rocznej
są stopami nominalnymi równoważnymi
zadanej efektywnej stopie rocznej ![]() .
.
2.2. Renty
Rent używa się w finansach i ubezpieczeniach przede wszystkim do ratalnej spłaty długów, do płacenia składek i do wypłaty emerytur.
Oto przykład wprowadzający.
Od 1 stycznia ![]() r. przez następne dziesięć lat będę otrzymywać
r. przez następne dziesięć lat będę otrzymywać
![]() zł na początku każdego roku. Jaka jest wartość tego ciągu wypłat
na 1 stycznia
zł na początku każdego roku. Jaka jest wartość tego ciągu wypłat
na 1 stycznia ![]() r.?
Każdą
z
r.?
Każdą
z ![]() płatności trzeba zdyskontować na dziś, tak więc
płatności trzeba zdyskontować na dziś, tak więc
gdzie ![]() jest czynnikiem dyskontującym. Skrót PV oznacza po angielsku
present value, czyli
wartość obecną tego strumienia wypłat. Nie jest to w zasadzie pojęcie
dla nas nowe. Wzór (2.3) przedstawia, na przykład, wartość
obecną pojedynczej wypłaty
jest czynnikiem dyskontującym. Skrót PV oznacza po angielsku
present value, czyli
wartość obecną tego strumienia wypłat. Nie jest to w zasadzie pojęcie
dla nas nowe. Wzór (2.3) przedstawia, na przykład, wartość
obecną pojedynczej wypłaty ![]() , dokonywanej za rok. Ponieważ tego
typu wielkości będą się pojawiać regularnie, wprowadzamy oznaczenie
, dokonywanej za rok. Ponieważ tego
typu wielkości będą się pojawiać regularnie, wprowadzamy oznaczenie
![]() na wartość obecną
na wartość obecną ![]() złotówek otrzymywanych
co rok, od dziś włącznie (tak więc ostatnia
złotówek otrzymywanych
co rok, od dziś włącznie (tak więc ostatnia ![]() –ta wpłata wpłynie
po
–ta wpłata wpłynie
po ![]() latach). Podobnie jak wyżej
latach). Podobnie jak wyżej
Sytuację tę zilustrowano na rys.2. Ze wzoru na sumę ciągu geometrycznego i ze wzoru (2.6) otrzymujemy
| (2.13) |
Po przekształceniu uzyskujemy wzór
| (2.14) |
który ma piękną interpretację.
Prawa strona wzoru: pożyczamy komuś ![]() zł (dziś). Strona lewa:
nasz dłużnik spłaca nam na bieżąco odsetki – na początku
każdego roku przez
zł (dziś). Strona lewa:
nasz dłużnik spłaca nam na bieżąco odsetki – na początku
każdego roku przez ![]() lat, w ten sposób dług zasadniczy nie zwiększa się.
Po
lat, w ten sposób dług zasadniczy nie zwiększa się.
Po ![]() okresach zwraca nam pożyczone
okresach zwraca nam pożyczone ![]() zł, które
zdyskontowane na dziś wynosi
zł, które
zdyskontowane na dziś wynosi ![]() .
.
Ponieważ płatności rat
renty są na ogół częstsze niż raz do roku (np. miesięczne),
potrzebne są dodatkowe oznaczenia. Załóżmy, że płatności
będą dokonywane przez ![]() lat
lat ![]() razy w ciągu roku, każda w wysokości
razy w ciągu roku, każda w wysokości
![]() zł. Wartość obecną renty oznaczamy symbolem
zł. Wartość obecną renty oznaczamy symbolem
(![]() to liczba wszystkich rat). Na podstawie (2.9) i (2.6)
mamy
to liczba wszystkich rat). Na podstawie (2.9) i (2.6)
mamy
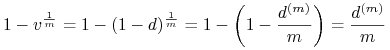 |
tak więc ostatecznie
| (2.15) |
Wzór ten równie łatwo zapamiętać jak (2.13).
Użyte powyżej symbole ![]() ,
, ![]() dotyczą rent płatnych z góry (pierwsza rata
od razu) – dwie kropki na górze oznaczają taką sytuację. Odpowiednie symbole bez kropek
oznaczają wartości obecne strumieni płatności przesuniętych o
dotyczą rent płatnych z góry (pierwsza rata
od razu) – dwie kropki na górze oznaczają taką sytuację. Odpowiednie symbole bez kropek
oznaczają wartości obecne strumieni płatności przesuniętych o
![]() rok w przyszłość (płatnych z dołu). Otrzymujemy wzory
rok w przyszłość (płatnych z dołu). Otrzymujemy wzory
Na zakończenie rozważmy możliwość (przynajmniej teoretyczną)
ciągłego napływu gotówki na nasz rachunek bankowy. Załóżmy, że
w ciągu roku wpływa nań ![]() zł. Tak więc między
zł. Tak więc między ![]() a
a ![]() marca
wpływa
marca
wpływa ![]() zł. Gotówka, która wpływa w krótkim przedziale
czasu między
zł. Gotówka, która wpływa w krótkim przedziale
czasu między ![]() a
a ![]() , jest w przybliżeniu dyskontowana
stałym czynnikiem
, jest w przybliżeniu dyskontowana
stałym czynnikiem ![]() (
(![]() ). Sumowanie
wartości obecnych poszczególnych wpłat zastąpimy tu oczywiście
całkowaniem
). Sumowanie
wartości obecnych poszczególnych wpłat zastąpimy tu oczywiście
całkowaniem
| (2.16) |
(skorzystaliśmy z (2.12)).




