6. Dodatek. Podstawowe pojęcia i twierdzenia teorii RRZ
6.1. Definicje
Pod równaniem różniczkowym zwyczajnym rozumiemy równanie postaci
| (6.1) |
gdzie ![]() jest czasem rzeczywistym (
jest czasem rzeczywistym (![]() to otwarty
odcinek),
to otwarty
odcinek), ![]() należy do przestrzeni fazowej (rozmaitości)
należy do przestrzeni fazowej (rozmaitości) ![]() a
a ![]() jest zależnym od czasu polem wektorowym na
jest zależnym od czasu polem wektorowym na ![]()
![]() spełnia
spełnia ![]() Często
Często ![]() jest
podzbiorem otwartym przestrzeni euklidesowej
jest
podzbiorem otwartym przestrzeni euklidesowej ![]() wtedy
wtedy ![]() i mówimy o układzie równań różniczkowych zwyczajnych. Jeśli
i mówimy o układzie równań różniczkowych zwyczajnych. Jeśli ![]() nie zależy od
czasu,
nie zależy od
czasu, ![]() , to równanie (6.1) jest równaniem
autonomicznym (a
, to równanie (6.1) jest równaniem
autonomicznym (a ![]() jest autonomicznym polem wektorowym), w
przeciwnym przypadku mamy do czynienia z nieautonomicznym równaniem.
Przestrzeń
jest autonomicznym polem wektorowym), w
przeciwnym przypadku mamy do czynienia z nieautonomicznym równaniem.
Przestrzeń ![]() nazywa się rozszerzoną
przestrzenią fazową.
nazywa się rozszerzoną
przestrzenią fazową.
Rozwiązaniem równania (6.1) nazywamy dowolną różniczkowalną krzywą ![]()
![]() która spełnia równanie
która spełnia równanie
Zagadnieniem początkowym nazywamy następujące dwa warunki
| (6.2) |
z których drugi nazywa się warunkiem początkowym. Rozwiązaniem zagadnienia początkowego (6.2) nazywamy rozwiązanie
równania (6.1), które ma własność ![]()
Jeśli ![]() jest rozwiązaniem układu (6.1), to krzywą
jest rozwiązaniem układu (6.1), to krzywą
![]() (tj. wykres rozwiązania) nazywamy krzywą całkową; jeśli, dodatkowo, układ (6.1) jest autonomiczny, to krzywą
(tj. wykres rozwiązania) nazywamy krzywą całkową; jeśli, dodatkowo, układ (6.1) jest autonomiczny, to krzywą ![]() (tj. obraz rozwiązania) nazywamy krzywą fazową.
(tj. obraz rozwiązania) nazywamy krzywą fazową.
Uwaga 6.1. Wprowadzając nowy czas ![]() możemy przepisać nieautonomiczne równanie (6.1) w postaci następującego układu autonomicznego
możemy przepisać nieautonomiczne równanie (6.1) w postaci następującego układu autonomicznego
| (6.3) |
w rozszerzonej przestrzeni fazowej. Wtedy krzywe całkowe dla równania (6.1) okażą się krzywymi fazowymi dla układu (6.3).
Równanie różniczkowe rzędu![]() , czyli
, czyli
| (6.4) |
zastępuje się układem równań pierwszego rzędu
| (6.5) |
przy pomocy podstawienia ![]()
![]()
![]() Naturalnym warunkiem początkowym dla równania
(6.4) jest
Naturalnym warunkiem początkowym dla równania
(6.4) jest
| (6.6) |
Zauważmy, że stosując trick z Uwagi 6.1 możemy zastąpić (na ogól) nieautonomiczny układ (6.5) odpowiednim układem
autonomicznym w ![]()
Uwaga 6.2. W książkach o równaniach różniczkowych rozważane są także równania uwikłane względem pochodnej, typu
| (6.7) |
Okazuje się, że, jeśli równanie ![]() da się
rozwikłać w otoczeniu pewnego punktu
da się
rozwikłać w otoczeniu pewnego punktu ![]() w postaci
w postaci ![]() to równanie (6.7) można przepisać w
postaci układu autonomicznego
to równanie (6.7) można przepisać w
postaci układu autonomicznego
gdzie ![]() jest nowym `czasem'. Rzeczywiście, mamy
jest nowym `czasem'. Rzeczywiście, mamy ![]() Zatem, różniczkując tożsamość
Zatem, różniczkując tożsamość ![]() dostajemy warunek
dostajemy warunek ![]() Jest on spełniony dla powyższego
pola wektorowego.
Jest on spełniony dla powyższego
pola wektorowego.
Podobny układ można napisać, gdy równanie ![]() rozwikłuje się względem
rozwikłuje się względem ![]() a także gdy
a także gdy ![]() i
i ![]() W tym skrypcie równania typu (6.7) nie są badane,
ale przytoczyliśmy je, aby zademonstrować pewną uniwersalną własność autonomicznych równań różniczkowych.
W tym skrypcie równania typu (6.7) nie są badane,
ale przytoczyliśmy je, aby zademonstrować pewną uniwersalną własność autonomicznych równań różniczkowych.
Z autonomicznym równaniem
| (6.8) |
wiąże się pojęcie potoku fazowego. Zauważmy, że rozwiązania ![]() równania (6.8) z warunkiem początkowym
równania (6.8) z warunkiem początkowym ![]() zadają rodzinę odwzorowań
zadają rodzinę odwzorowań
gdzie ![]() jest dziedziną odwzorowania
jest dziedziną odwzorowania ![]() Ta rodzina powinna spełniać dwie naturalne własności
Ta rodzina powinna spełniać dwie naturalne własności
| (6.9) | |||||
| (6.10) |
Własność (6.9) to definicja warunku początkowego. Własność (6.10), która powinna być spełniona dla ![]() oznacza, że jeśli wystartujemy w
momencie czasu
oznacza, że jeśli wystartujemy w
momencie czasu ![]() z punktu
z punktu ![]() i dojedziemy (wzdłuż rozwiązania) do punktu
i dojedziemy (wzdłuż rozwiązania) do punktu ![]() a następnie wyzerowujemy stoper i
jedziemy z
a następnie wyzerowujemy stoper i
jedziemy z ![]() po czasie
po czasie ![]() to dojedziemy do tego samego punktu, jak byśmy jechali po czasie s
to dojedziemy do tego samego punktu, jak byśmy jechali po czasie s ![]() z
z ![]() bez zerownia stopera. Oczywiście, tutaj istotne jest, że
bez zerownia stopera. Oczywiście, tutaj istotne jest, że ![]() (autonomiczność).
(autonomiczność).
Rodzina ![]()
![]() spełniająca warunki (6.9)–(6.10) nazywa się lokalnym
potokiem fazowym. Rodzina
spełniająca warunki (6.9)–(6.10) nazywa się lokalnym
potokiem fazowym. Rodzina
(globalnych) dyfeomorfizmów przestrzeni fazowej ![]() spełniająca własności (6.9)–(6.10) nazywa się potokiem fazowym na
spełniająca własności (6.9)–(6.10) nazywa się potokiem fazowym na ![]() Inaczej mówiąc, odwzorowanie
Inaczej mówiąc, odwzorowanie ![]() jest
homomorfizmen z grupy
jest
homomorfizmen z grupy ![]() do grupy
do grupy ![]() dyfeomorfizmów
rozmaitości
dyfeomorfizmów
rozmaitości ![]()
Przykład 6.3. Równanie
definiuje globalne pole wektorowe na przestrzeni rzutowej ![]() (gdzie współrzędna
(gdzie współrzędna ![]() w otoczniu
w otoczniu ![]() spełnia równanie
spełnia równanie ![]() Tutal lokalny potok
fazowy okazuje sie być potokiem fazowym na
Tutal lokalny potok
fazowy okazuje sie być potokiem fazowym na ![]() złożonym z przekształceń Möbiusa
złożonym z przekształceń Möbiusa
Uwaga 6.4. W przypadku nieautonomicznego pola wektorowego mamy do
czynienia z ![]() parametrową rodziną przekształceń
parametrową rodziną przekształceń
(ściślej, z jej lokalną wersją) definiowaną tak, że ![]() czyli wartość w chwili
czyli wartość w chwili ![]() rozwiązania startującego z
rozwiązania startującego z ![]() w chwili
w chwili ![]() Zachodzą
oczywiste tożsamości
Zachodzą
oczywiste tożsamości
6.2. Twierdzenia
Poniżej czytelnik znajdzie szereg twierdzeń, które są podstawowe w teorii równań różniczkowych zwyczajnych i które są podane bez dowodów. Po więcej szczegółów odsyłam do [3], [15].
Twierdzenie 6.5 (O istnieniu i jednoznaczności lokalnych
rozwiązań). Załóżmy, że pole ![]() jest klasy
jest klasy ![]() na zbiorze otwartym
na zbiorze otwartym ![]() Niech
Niech ![]()
Wtedy istnieje odcinek ![]() zawierający
moment początkowy
zawierający
moment początkowy ![]() oraz otoczenie
oraz otoczenie ![]() punktu
punktu ![]() takie, że dla dowolnego
takie, że dla dowolnego ![]() zagadnienie początkowe
zagadnienie początkowe ![]()
![]() posiada dokładnie jedno rozwiązanie
posiada dokładnie jedno rozwiązanie ![]()
Ponadto odwzorowanie
| (6.11) |
jest ciągłe, a w przypadku, gdy pole ![]() jest
analityczne, to to odwzorowanie też jest analityczne.
jest
analityczne, to to odwzorowanie też jest analityczne.
Przypomnimy, że podstawowa idea dowodu tego twierdzenia polega na zastąpieniu zagadnienia początkowego (6.2) równaniem całkowym
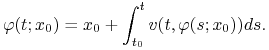 |
(6.12) |
To równanie jest traktowane jako równanie punktu stałego ![]() dla operatora
dla operatora ![]() definiowanego po prawej
stronie równania (6.12) działającego w odpowiedniej przestrzeni
Banacha odwzorowań
definiowanego po prawej
stronie równania (6.12) działającego w odpowiedniej przestrzeni
Banacha odwzorowań ![]() Na ogół jest to przestrzeń Banacha funkcji ciągłych na
Na ogół jest to przestrzeń Banacha funkcji ciągłych na ![]() z normą
supremum, przy tym warunek zwężania dla operatora
z normą
supremum, przy tym warunek zwężania dla operatora ![]() wynika z
warunku Lipschitza względem
wynika z
warunku Lipschitza względem ![]() dla pola
dla pola ![]() W przypadku
analitycznym jako przestrzeń Banacha wybiera się przestrzeń
funkcji holomorficznych w pewnym obszarze w
W przypadku
analitycznym jako przestrzeń Banacha wybiera się przestrzeń
funkcji holomorficznych w pewnym obszarze w ![]() z normą supremum (Zadanie 6.25)
z normą supremum (Zadanie 6.25)
Przykład 6.6. Równanie
posiada dwa rozwiązania z tym samym warunkiem początkowym ![]() :
: ![]() dla
dla ![]() i
i ![]() dla
dla ![]() oraz
oraz ![]() Ten standardowy przykład pokazuje, jak ważny jest warunk Lipschitza; tutaj on nie zachodzi w
Ten standardowy przykład pokazuje, jak ważny jest warunk Lipschitza; tutaj on nie zachodzi w ![]()
Twierdzenie 6.7 (O zależności od warunku
początkowego). Jeśli w Twierdzeniu 6.5 założymy, że ![]() jest klasy
jest klasy ![]() , to odwzorowanie (6.11) będzie klasy
, to odwzorowanie (6.11) będzie klasy ![]() Ogólniej, jeśli
Ogólniej, jeśli ![]() jest klasy
jest klasy ![]()
![]() to
to ![]() jest klasy
jest klasy ![]()
Twierdzenie 6.8 (O zależności od parametrów). 19W niektórych źródłach (np. [13], [12]) dowodzi się klasy ![]() zależności rozwiązań od parametrów. Dla naszych celów klasa
zależności rozwiązań od parametrów. Dla naszych celów klasa ![]() jest wystarczająca, zwłaszcza, jeśli uwzględni się prostotę poniższego szkicu dowodu tego twierdzenia.
Jeśli pole
jest wystarczająca, zwłaszcza, jeśli uwzględni się prostotę poniższego szkicu dowodu tego twierdzenia.
Jeśli pole ![]() zależy dodatkowo od parametru
zależy dodatkowo od parametru ![]() i
i ![]() jest klasy
jest klasy ![]()
![]() to rozwiązanie
to rozwiązanie ![]() jest klasy
jest klasy ![]()
W dowodach ostatnich dwóch twierdzeń wykorzystuje się ważnie pojęcie równania w wariacjach. Równaniem w wariacjach względem warunku początkowego nazywamy równanie
| (6.13) |
Tutaj ![]()
![]() , jest zadanym rozwiązaniem, a równanie (6.13) otrzymuje się przez podstawienie
zaburzenia
, jest zadanym rozwiązaniem, a równanie (6.13) otrzymuje się przez podstawienie
zaburzenia ![]() (z małym
(z małym ![]() ) do zagadnienia początkowego (6.2) z warunkiem początkowym
) do zagadnienia początkowego (6.2) z warunkiem początkowym ![]() i przyrównania wyrazów rzędu
i przyrównania wyrazów rzędu ![]() Pochodną czastkową
Pochodną czastkową ![]() rozwiązania względem warunku początkowego
otrzymuje się jako rozwiązanie układu (6.13) z warunkiem początkowym
rozwiązania względem warunku początkowego
otrzymuje się jako rozwiązanie układu (6.13) z warunkiem początkowym ![]() (gdzie
(gdzie ![]() to standardowa baza w
to standardowa baza w ![]()
Równaniem w wariacjach względem parametru nazywamy równanie
| (6.14) |
Tutaj ![]() jest wyróżnionym rozwiązaniem
zagadnienia początkowego
jest wyróżnionym rozwiązaniem
zagadnienia początkowego ![]()
![]() tzn. dla ustalonego parametru
tzn. dla ustalonego parametru ![]() i macierz
i macierz ![]() jest taka sama jak w (6.13). To równanie otrzymuje się przez
podstawienie
jest taka sama jak w (6.13). To równanie otrzymuje się przez
podstawienie ![]() do
zagadnienia początkowego
do
zagadnienia początkowego ![]()
![]() i porównanie wyrazów liniowych względem małego
i porównanie wyrazów liniowych względem małego ![]()
W dowodach Twierdzeń 6.7 i 6.8 problem sprowadza się do układu ![]()
![]() lub do układu
lub do układu ![]()
![]() i
stosuje Twierdzenie 6.5 (Zadania 6.26 i 6.27).
i
stosuje Twierdzenie 6.5 (Zadania 6.26 i 6.27).
Z powyższych twierdzeń wynikają ważne wnioski o jakościowym zachowaniu się rozwiązań równania (6.1).
Twierdzenie 6.9 (O prostowaniu dla układu nieautonomicznego)
. Jeśli ![]() jest klasy
jest klasy ![]()
![]() i
i ![]() to istnieje lokalny dyfeomeorfizm
to istnieje lokalny dyfeomeorfizm
z otoczenia punktu ![]() który przeprowadza układ (6.1) w układ
który przeprowadza układ (6.1) w układ
W dowodzie dyfeomeorfizm ![]() jest definiowany tak, że jeśli punkt
jest definiowany tak, że jeśli punkt ![]() , tj. jest wartością rozwiązania po
czasie
, tj. jest wartością rozwiązania po
czasie ![]() i z warunkiem początkowym
i z warunkiem początkowym ![]() , to kładziemy
, to kładziemy ![]() (Zadanie 6.28).
(Zadanie 6.28).
Twierdzenie 6.10 (O prostowaniu dla układu autonomicznego)
. Jeśli autonomiczne pole wektorowe ![]() jest klasy
jest klasy ![]()
![]() na
na ![]() i punkt
i punkt ![]() jest taki, że
jest taki, że
| (6.15) |
to istnieje lokalny dyfeomorfizm ![]() z
otoczenia punktu
z
otoczenia punktu ![]() , który przeprowadza układ
, który przeprowadza układ ![]() w układ
w układ
Jak można się domyślić, zmienna ![]() to czas
to czas ![]() wdłuż rozwiązań
wdłuż rozwiązań ![]() które startują przy
które startują przy ![]() z pewnej hiperpłaszczyzny
z pewnej hiperpłaszczyzny ![]() prostopadłej do wektora
prostopadłej do wektora ![]() Pozostałe zmienne
Pozostałe zmienne ![]() pochodzą od jakiegoś układu współrzędnych na hiperpłaszczyźnie
pochodzą od jakiegoś układu współrzędnych na hiperpłaszczyźnie ![]() i są stałe wzdłuż rozwiązań (Zadanie 6.29).
i są stałe wzdłuż rozwiązań (Zadanie 6.29).
Uwaga 6.11. Powyższe twierdzenie można nazwać pierwszym twierdzeniem jakościowej teorii równań różniczkowych zwyczajnych.20W angojęzycznej literaturze występuje ono pod nazwą `Flow Box Theorem'. Mówi ono, że lokalnie każde pole wektorowe spełniające warunek (6.15) jest takie samo z matematycznego punktu widzenia. Istotne różnice pojawiają się przy badaniu zachowania globalnych rozwiązań. Warunek (6.15) implikuje pewną prostotę pola wektorowego. W pierwszym rozdziale niniejszego skryptu badamy sytuację gdy ten warunek jest naruszony.
Twierdzenie 6.12 (O lokalnym potoku fazowym). Dla autonomicznego pola wektorowego ![]() klasy
klasy ![]()
![]() istnieje lokalny potok fazowy
istnieje lokalny potok fazowy ![]()
![]() (spełniający
warunki (6.9)–(6.10)) zadany przez rozwiązania
(spełniający
warunki (6.9)–(6.10)) zadany przez rozwiązania ![]() zagadnień początkowych
zagadnień początkowych ![]()
![]()
Oczywiście to twierdzenie jest natychmiastową konsekwencją
twierdzenia o istnieniu i jednoznaczności lokalnych rozwiązań
dla układu (6.1) z autonomicznym polem ![]()
Twierdzenie 6.13 (O przedłużniu rozwiązań). Niech pole ![]() będzie klasy
będzie klasy ![]()
![]() w zbiorze otwarym
w zbiorze otwarym ![]() i niech
i niech ![]() będzie zwarym podzbiorem. Wtedy dowolne lokalne rozwiązanie
będzie zwarym podzbiorem. Wtedy dowolne lokalne rozwiązanie ![]() starujące z
starujące z ![]() albo przedłuża się dla wszystkich czasów
albo przedłuża się dla wszystkich czasów ![]() pozostając w
pozostając w ![]() albo wychodzi z
albo wychodzi z ![]() po skończonym czasie
po skończonym czasie ![]()
Taka sama alternatywa ma miejsce dla rozwiązań ![]() przy
przy![]() .
.
W pewnym sensie to twierdzenie jest oczywiste. Następujący przykład pokazuje, że założenie o zwartości ![]() jest istotne.
jest istotne.
Przykład 6.14. Równanie
ma rozwiązania ![]() które uciekają do
nieskończoności po skończonym czasie
które uciekają do
nieskończoności po skończonym czasie ![]()
6.3. Metody rozwiązywania
Poniżej przedstawiamy listę klas równań różniczkowych zwyczajnych, które dają się scałkowac i podajemy metody ich całkowania. Wszystkie rozważane tutaj równania mają postać
| (6.16) |
albo równoważną postać równania Pfaffa
Przykład 6.15.Równania z rozdzielonymi zmiennymi. Są to równania postaci
Oczywiście rozwiązania są zadane w postaci uwikłanej
Przykład 6.16.Równania jednorodne są postaci
Tutaj podstawienie ![]() prowadzi do równania z rozdzielonymi
zmiennymi
prowadzi do równania z rozdzielonymi
zmiennymi
Do tej klasy można zaliczyć równania postaci
Poprzez przesunięcie początku układu współrzędnych do
punktu przecięcia się prostych ![]() i
i ![]() staje się ono ewidentnie jednorodne. Gdy
staje się ono ewidentnie jednorodne. Gdy ![]() równanie łatwo sprowadza się do równania o zmiennych rozdzielonych.
równanie łatwo sprowadza się do równania o zmiennych rozdzielonych.
Przykład 6.17.Równania quasi-jednorodne charakteryzują się niezmienniczością względem symetrii typu
która uogólnia analogiczną symetrię z ![]() dla równania jednorodnego. Tutaj podstawienie
dla równania jednorodnego. Tutaj podstawienie ![]() prowadzi do równania z rozdzielonymi zmiennymi.
prowadzi do równania z rozdzielonymi zmiennymi.
Przykład 6.18.Równania liniowe
| (6.17) |
dzielą się na jednorodne, gdy ![]() i niejednorodne. Ogólne rozwiązanie równania jednorodnego
i niejednorodne. Ogólne rozwiązanie równania jednorodnego ![]() stowarzyszonego z równaniem (6.17) ma postać
stowarzyszonego z równaniem (6.17) ma postać
gdzie ![]() jest funkcją pierwotną dla funkcji
jest funkcją pierwotną dla funkcji ![]() Ogólne
rozwiązanie równania niejednorodnego jest sumą ogólnego
rozwiązania równania jednorodnego
Ogólne
rozwiązanie równania niejednorodnego jest sumą ogólnego
rozwiązania równania jednorodnego ![]() i pewnego szczególnego rozwiązania
i pewnego szczególnego rozwiązania ![]() równania niejednorodnego.
To ostatnie rozwiązanie poszukujemy metodą uzmienniania
sta łej, tzn. w postaci
równania niejednorodnego.
To ostatnie rozwiązanie poszukujemy metodą uzmienniania
sta łej, tzn. w postaci
Po podstawieniu do równania (6.17) dostajemy równanie ![]()
Ogólne rozwiązanie ma postać
| (6.18) |
Przykład 6.19.Równanie Bernoulliego
sprowadza się do równania liniowego przez podstawienie
Przykład 6.20.Równanie z czynnikiem całkującym ma postać
lub
Tutaj ![]() jest czynnikiem całkującym a
jest czynnikiem całkującym a ![]() jest całką pierwszą równania, tzn. funkcja
jest całką pierwszą równania, tzn. funkcja ![]() jest
stała na krzywych całkowych równania,
jest
stała na krzywych całkowych równania, ![]() Oczywiście, tutaj rozwiązania
Oczywiście, tutaj rozwiązania ![]() są uwikłane w postaci równań
są uwikłane w postaci równań
Naturalne jest pytanie, jak z postaci funkcji ![]() i
i ![]() odgadnąć, czy istnieje czynnik całkujący i całka pierwsza. Wygodnie jest
operować autonomicznym polem wektorowym
odgadnąć, czy istnieje czynnik całkujący i całka pierwsza. Wygodnie jest
operować autonomicznym polem wektorowym
| (6.19) |
związanym z równaniem (6.16).
Zauważmy, że przypadek z ![]() z całką pierwszą
z całką pierwszą ![]() odpowiada sytuacji, gdy układ (6.19) jest hamiltonowski z
odpowiada sytuacji, gdy układ (6.19) jest hamiltonowski z ![]() jako funkcją Hamiltona (hamiltonianem),
jako funkcją Hamiltona (hamiltonianem),
Oczywiście wtedy mamy
| (6.20) |
tzn. dywergencja pola wektorowego ![]() zeruje się, lub, równoważnie,
zeruje się, lub, równoważnie,
Jest to warunek konieczny dla hamiltonowskości układu (6.19). Gdy ![]() to można zdefiniować funkcję
to można zdefiniować funkcję ![]() następująco
następująco
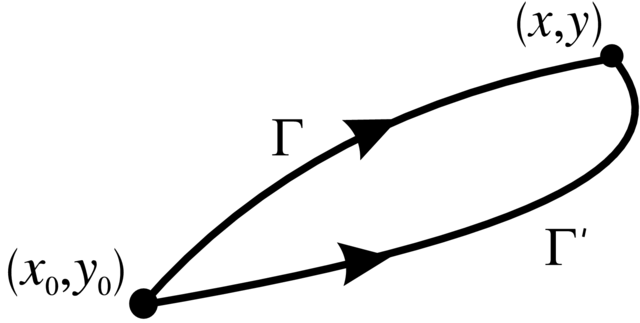
gdzie ![]() jest drogą z ustalonego punktu
jest drogą z ustalonego punktu ![]() do
do ![]() Jeśli obszar
Jeśli obszar ![]() , w którym jest zdfiniowany układ (6.19) jest jednospójny (każda pętla jest ściągalna do punktu), to
definicja
, w którym jest zdfiniowany układ (6.19) jest jednospójny (każda pętla jest ściągalna do punktu), to
definicja ![]() nie zależy od wyboru drogi
nie zależy od wyboru drogi ![]() różnica pomiędzy tą wartością i wartością
zdefiniowaną dla innej drogi
różnica pomiędzy tą wartością i wartością
zdefiniowaną dla innej drogi ![]() jest całką po
zamkniętej pętli
jest całką po
zamkniętej pętli ![]() (która ogranicza
obszar
(która ogranicza
obszar ![]() z
z ![]() formy
formy ![]() która jest zamknięta, zatem wzór Stokes'a daje
która jest zamknięta, zatem wzór Stokes'a daje ![]()
Przykład równania
w ![]() które spełnia warunek (6.20), i posiada
lokalną (ale nie globalną) całkę pierwszą
które spełnia warunek (6.20), i posiada
lokalną (ale nie globalną) całkę pierwszą ![]() pokazuje, że założenie jednospójności jest
istotne.
pokazuje, że założenie jednospójności jest
istotne.
Przypadek, gdy istnieje nietrywialny czynnik całkujący ![]() jest dużo trudniejszy. Pozwolę sobie tutaj zacytować wynik M. Singera, który dotyczy przypadku, gdy
jest dużo trudniejszy. Pozwolę sobie tutaj zacytować wynik M. Singera, który dotyczy przypadku, gdy ![]() i
i ![]() są wielomianami.
są wielomianami.
Twierdzenie 6.21 (Singer). Jeśli równanie (6.16) z
wielomanami ![]() i
i ![]() posiada czynnik całkujący
posiada czynnik całkujący ![]() i całkę pierwszą, które można przedstawić
w kwadraturach, to czynnik całkujący
i całkę pierwszą, które można przedstawić
w kwadraturach, to czynnik całkujący ![]() można wybrać
w tzw. postaci Darboux
można wybrać
w tzw. postaci Darboux
gdzie ![]() jest funkcją wymierną,
jest funkcją wymierną, ![]() są wielomianami a
są wielomianami a![]()
Odsyłam czytelnika do książki [20], w której można znaleźć definicję funkcji przedstawialnych w kwadraturach oraz dowód twierdzenia Singera.
6.4. Układy i równania liniowe
Układy liniowe równań różniczkowych zwyczajnych są uogólnieniami równań (6.17) i mają postać
| (6.21) |
Równolegle rozpatruje się liniowe równania różniczkowe rzędu ![]() postaci
postaci
| (6.22) |
Wiadomo, że rozwiązania ![]() takich układów
i równań przedłużają się do całego odcinka
takich układów
i równań przedłużają się do całego odcinka ![]() (Zadanie 6.40). W przypadku jednorodnym, tzn. gdy
(Zadanie 6.40). W przypadku jednorodnym, tzn. gdy ![]() zbiór
rozwiązań tworzy
zbiór
rozwiązań tworzy ![]() wymiarową przestrzeń wektorową. Każda baza tej przestrzeni tworzy tzw. układ fundamentalny
wymiarową przestrzeń wektorową. Każda baza tej przestrzeni tworzy tzw. układ fundamentalny ![]() Taki układ fundamentalny zadaje
macierz fundamentalną
Taki układ fundamentalny zadaje
macierz fundamentalną ![]() w przypadku układu (6.21) i
w przypadku układu (6.21) i
![\mathcal{F}(t)=\left(\begin{array}[]{ccc}\varphi _{{1}}&\ldots&\varphi _{{n}}\\
\varphi _{{1}}^{{(1)}}&\ldots&\varphi _{{n}}^{{(1)}}\\
\ldots&\ldots&\ldots\\
\varphi _{{1}}^{{(n-1)}}&\ldots&\varphi _{{n}}^{{(n-1)}}\end{array}\right)](wyklady/rrj/mi/mi2287.png) |
w przypadku równania (6.22). Wyznacznik macierzy fundamentalnej nazy- wa się Wrońskianem
| (6.23) |
(od nazwiska polskiego matematyka J. Hoene-Wrońskiego).
Ogólne rozwiązanie układu jednorodnego (6.21) (z ![]() ) ma
postać
) ma
postać
| (6.24) |
gdzie ![]() jest stałym wektorem (wyznaczanym z warunków początkowych); w szczególności, gdy układ fundamentalny jest tak
dobrany aby
jest stałym wektorem (wyznaczanym z warunków początkowych); w szczególności, gdy układ fundamentalny jest tak
dobrany aby ![]() to rozwiązanie
to rozwiązanie ![]() spełnia warunek początkowy
spełnia warunek początkowy ![]() W
przypadku jednorodnego równania (6.22) (z
W
przypadku jednorodnego równania (6.22) (z ![]() ) ogólne rozwiązanie ma postać
) ogólne rozwiązanie ma postać
tzn. pierwsza składowa wektora stojącego po prawej stronie równania (6.24).
Nietrudno domyślić się, że ogólne rozwiązanie układu lub równania niejednorodnego (tj. z ![]() jest sumą
ogólnego rozwiązania równania jednorodnego
jest sumą
ogólnego rozwiązania równania jednorodnego ![]() i
szczególnego rozwiązania układu lub równania niejednorodnego
i
szczególnego rozwiązania układu lub równania niejednorodnego ![]() Aby rozwiązać układ lub równanie
niejednorodne, znając macierz fundamentalną, stosujemy metodę uzmienniania stałych, tzn. robimy podstawienie
Aby rozwiązać układ lub równanie
niejednorodne, znając macierz fundamentalną, stosujemy metodę uzmienniania stałych, tzn. robimy podstawienie ![]() Rozwiązując odpowiednie równanie na
Rozwiązując odpowiednie równanie na ![]() znajdziemy ogólne rozwiązanie układu (6.21) w postaci
znajdziemy ogólne rozwiązanie układu (6.21) w postaci
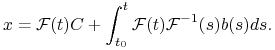 |
Oczywiście, podstawowym problemem jest znalezienie macierzy
fundamentalnej ![]()
W przypadku, gdy macierz ![]() w układzie (6.21) lub współczynniki
w układzie (6.21) lub współczynniki ![]() w równaniu (6.22) nie zależą od czasu,
mówimy o układzie o stałych współczynnikach lub o
równaniu o stałych współczynnikach. W tym przypadku
macierz fundamentalna ma postać
w równaniu (6.22) nie zależą od czasu,
mówimy o układzie o stałych współczynnikach lub o
równaniu o stałych współczynnikach. W tym przypadku
macierz fundamentalna ma postać
gdzie
![A=\left(\begin{array}[]{ccccc}0&1&0&\ldots&0\\
0&0&1&\ldots&0\\
\ldots&\ldots&\ldots&\ldots&\ldots\\
-a_{{0}}&-a_{{1}}&-a_{{2}}&\ldots&-a_{{n-1}}\end{array}\right)](wyklady/rrj/mi/mi2084.png) |
w przypadku równania.
Dla równania (6.21) o stałych współczynnikach ogólne rozwiązanie równania jednorodnego można otrzymać bezpośrednio z równania charakterystycznego
| (6.25) |
Ma ono postać
| (6.26) |
gdzie ![]() są pierwiastkami równania charakterystycznego
krotności
są pierwiastkami równania charakterystycznego
krotności ![]() ; w przypadku występowania par zespolonych
pierwiastków
; w przypadku występowania par zespolonych
pierwiastków ![]()
![]() odpowiednie wspólczynniki w sumie w (6.26) są sprzężone,
odpowiednie wspólczynniki w sumie w (6.26) są sprzężone, ![]() i te dwa składniki dają
wyrażenie
i te dwa składniki dają
wyrażenie
(ze stałymi ![]() i
i ![]() ).
).
Również istnieje recepta na szczególne rozwiązanie
niejednorodnego równania (6.22) o stałych współczynnikach, w
przypadku gdy funkcja ![]() (po prawej stronie równania) jest tzw.
quasi-wielomianem postaci
(po prawej stronie równania) jest tzw.
quasi-wielomianem postaci
| (6.27) |
Tutaj ![]() nazywa się wykładnikiem quasi-wielomianu a
nazywa się wykładnikiem quasi-wielomianu a ![]() jest
zwykłym wielomianem stopnia
jest
zwykłym wielomianem stopnia ![]() , nazywanym stopniem quasi-wielomianu. Również funkcje postaci
, nazywanym stopniem quasi-wielomianu. Również funkcje postaci ![]() i
i ![]() są odpowiednio częściamu rzeczywistą i urojoną quasi-wielomianu z zespolonym wykładnikiem
są odpowiednio częściamu rzeczywistą i urojoną quasi-wielomianu z zespolonym wykładnikiem ![]()
Twierdzenie 6.22. Rozwiązanie ogólne równania jednorodnego ma postać (6.26).
Jeśli prawa strona równania niejednorodnego (6.22) ma postać (6.27) i wykładnik ![]() quasiwielomianu jest
pierwiastkiem równania charakterystycznego (6.25) krotności
quasiwielomianu jest
pierwiastkiem równania charakterystycznego (6.25) krotności ![]() to szczególne rozwiązanie równania można wybrać
w postaci quasi-wielomianu
to szczególne rozwiązanie równania można wybrać
w postaci quasi-wielomianu
gdzie ![]() jest wielomianem stopnia
jest wielomianem stopnia![]() .
.
Następujące twierdzenie, pochodzące od J. Liouville'a, jest uogólnieniem elementarnej algebraicznej tożsamości
i ma olbrzymie zastosowanie w Jakościowej Teorii.
Twierdzenie 6.23 (Liouville). Wrońskian ![]() związany z macierzą fundamentalną
związany z macierzą fundamentalną ![]() układu (6.21) (wzór (6.23)) spełnia równanie
układu (6.21) (wzór (6.23)) spełnia równanie
Dowód sprowadza się do policzenia granicy
bo ![]() Latwo sprawdzić, korzystając ze standardowej definicji wyznacznika
Latwo sprawdzić, korzystając ze standardowej definicji wyznacznika ![]() , że człony pochodzące od nietrywialnych permutacji
, że człony pochodzące od nietrywialnych permutacji ![]() dają wkład rzędu
dają wkład rzędu ![]() . Człon
. Człon ![]() równa się
równa się ![]()
W przypadku gdy macierz fundamentalna ![]() spełnia własność
spełnia własność ![]() wyznacznik Wrońskiego ma naturalną
interpretację (
wyznacznik Wrońskiego ma naturalną
interpretację (![]() wymiarowej) objętości równoległościanu rozpiętego przez wektory
wymiarowej) objętości równoległościanu rozpiętego przez wektory ![]()
![]() gdzie
gdzie ![]() jest to
jest to ![]() parametrowa rodzina
przekształceń ewolucji układu (które są zdefiniowane w
Uwadze 6.4 i które są liniowe) a
parametrowa rodzina
przekształceń ewolucji układu (które są zdefiniowane w
Uwadze 6.4 i które są liniowe) a ![]() to
standardowa baza w
to
standardowa baza w ![]() Inaczej mówiąc, zachodzą tożsamości
Inaczej mówiąc, zachodzą tożsamości
| (6.28) |
dla obszaru ![]() gdzie
gdzie ![]() oznacza objętość.
oznacza objętość.
Zastosujmy tę obserwację do równania w wariacjach względem
warunków początkowych (6.13) w przypadku autonomicznego pola
wektorowego ![]() To równanie w wariacjach ma postać
To równanie w wariacjach ma postać ![]() gdzie
gdzie ![]() jest macierzą pochodnych cząstkowych
jest macierzą pochodnych cząstkowych ![]() składowych
składowych ![]() pola wzdłuż wyróżnionego rozwiązania
pola wzdłuż wyróżnionego rozwiązania
![]() Łatwo sprawdzić tożsamość
Łatwo sprawdzić tożsamość
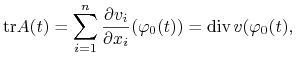 |
(6.29) |
gdzie div oznacza dywergencję.
Niech ![]() będzie obszarem takim, że rozwiązania starujące z
będzie obszarem takim, że rozwiązania starujące z ![]() są określone dla czasów pomiędzy
są określone dla czasów pomiędzy ![]() i
i ![]() Podzielmy obszar
Podzielmy obszar ![]() na prostokątne kostki
na prostokątne kostki ![]() o
małej krawędzi
o
małej krawędzi ![]() i z wyróżnionymi punktami
i z wyróżnionymi punktami ![]() . Pod działaniem potoku
. Pod działaniem potoku ![]() te kostki przejdą na nielinowe obszarki
te kostki przejdą na nielinowe obszarki ![]() , które są bliskie równoległościankom rozpiętym przez wektory
postaci
, które są bliskie równoległościankom rozpiętym przez wektory
postaci ![]() gdzie każdy wektor
gdzie każdy wektor ![]() jest jak powyżej dla przekształcenia
jest jak powyżej dla przekształcenia ![]() związanego z równaniem w wariacjach wzdłuż rozwiązania
związanego z równaniem w wariacjach wzdłuż rozwiązania ![]() startującego z
startującego z ![]() Następnie sumujemy objętości obszarków
Następnie sumujemy objętości obszarków ![]() i przechodzimy do granicy z
i przechodzimy do granicy z ![]() korzystając z własności (6.28) i (6.29). W
rezultacie otrzymujemy następujący wynik.
korzystając z własności (6.28) i (6.29). W
rezultacie otrzymujemy następujący wynik.
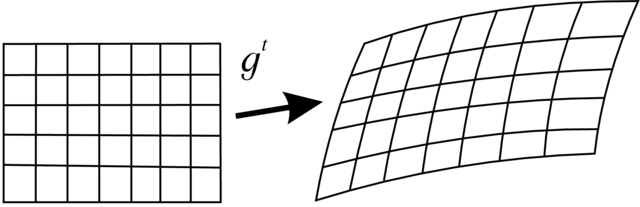
Twierdzenie 6.24. Dla obszaru![]() i potoku
i potoku ![]() generowanego przez autonomiczne pole
vektorowe
generowanego przez autonomiczne pole
vektorowe ![]() zachodzi tożsamość
zachodzi tożsamość
W szczególności, jeśli ![]() to potok
to potok ![]() ma własność zmniejsznia objętości, a jeśli
ma własność zmniejsznia objętości, a jeśli ![]() to potok ma własność rozszerzania obszarów.
to potok ma własność rozszerzania obszarów.
ZADANIA
Zadanie 6.25. W zależności od stałych ![]() i
i ![]() (stała Lipschitza) dobrać
(stała Lipschitza) dobrać ![]() w
w ![]() i promienie w kulach
i promienie w kulach ![]()
![]() i
i ![]() aby: (i)
aby: (i)
![]()
![]() oraz (ii)
oraz (ii)
![]() było kontrakcją na
było kontrakcją na ![]() To da uzupełnienie dowodu Twierszenia 6.5.
To da uzupełnienie dowodu Twierszenia 6.5.
Zadanie 6.26. Uzupełnić dowody Twierdzeń 6.7 i 6.8.
Wskazówka: W dowodzie Twierdzenia 6.7 rozważyć ciąg przybliżeń ![]()
![]() dla
zagadnienia początkowego
dla
zagadnienia początkowego ![]()
![]()
![]() , gdzie
, gdzie ![]() przyjmuje wartości w przestrzenie macierzy
przyjmuje wartości w przestrzenie macierzy ![]() W dowodzie
Twierdzenia 6.8 skorzystać z Twierdzenia 6.7.
W dowodzie
Twierdzenia 6.8 skorzystać z Twierdzenia 6.7.
Zadanie 6.27. Udowodnić, że jeśli ![]() zależy w sposób analityczny od zwoich argumentów, to rozwiązanie
zależy w sposób analityczny od zwoich argumentów, to rozwiązanie
![]() też jest analityczne.
też jest analityczne.
Zadanie 6.28. Uzupełnić dowód Twierdzenia 6.9.
Zadanie 6.29. Uzupełnić dowód twierdzenia 6.10.
Zadanie 6.30. Znaleźć rozwiązanie równania ![]() spełniające warunek
spełniające warunek ![]()
Zadanie 6.31. Rozwiązać równanie ![]()
Zadanie 6.32. Rozwiązać równanie ![]()
Zadanie 6.33. Rozwiązać równanie ![]()
Zadanie 6.34. Rozwiązać równanie ![]()
Zadanie 6.35. Rozwiązać równanie ![]()
Zadanie 6.36. Rozwiązać równanie ![]()
Zadanie 6.37. Rozwiązać następujące równanie
Riccatiego ![]()
Wskazówka: Zgadnąć jedno rozwiązanie.
Zadanie 6.38. Rozwiązać równanie ![]()
Wskazówka: Poszukać czynnika całkującego w postaci ![]()
Zadanie 6.39. Rozwiązać równanie ![]()
Zadanie 6.40. Rozważmy układ liniowy ![]() z
ciągłymi
z
ciągłymi ![]() i
i ![]() oraz z oszacowaniami
oraz z oszacowaniami ![]() i
i ![]() Pokazać oszacowania
Pokazać oszacowania ![]() gdzie ostatnia nierówność zachodzi dla dostatecznie dużych
gdzie ostatnia nierówność zachodzi dla dostatecznie dużych ![]() i pewnej ciągłej funkcji
i pewnej ciągłej funkcji ![]() Wywnioskować stąd, że rozwiązania nie mogą
uciec do nieskończoności po skończonym czasie.
Wywnioskować stąd, że rozwiązania nie mogą
uciec do nieskończoności po skończonym czasie.
Zadanie 6.41. Podać ogólne rozwiązanie układu ![]()
![]()
![]()
Zadanie 6.42. Podać ogólne rozwiązanie układu ![]()
![]()
Zadanie 6.43. Podać ogólne rozwiązanie równania ![]()
Zadanie 6.44. Podać ogólne rozwiązanie równania ![]()
Zadanie 6.45. Dla jakich ![]() i
i ![]() równanie
równanie ![]() posiada przynajmniej jedno okresowe rozwiązanie.
posiada przynajmniej jedno okresowe rozwiązanie.