Zagadnienia
1. Miary zależności i miary bliskości między zmiennymi
W rozdziale tym przedstawione zostaną wskaźniki liczbowe do analizy danych jedno- i dwuwymiarowych. Przypomniane zostaną miary rozrzutu oraz omówione miary zależności i miary bliskości między zmiennymi (cechami).
Główna różnica:
-
miary zależności: minimalne dla zmiennych niezależnych, maksymalne dla zmiennych identycznych;
-
miary bliskości (odległości, zróżnicowania): minimalne dla zmiennych identycznych;
Wygodnie jest podzielić zmienne na ilościowe (liczbowe), porządkowe i jakościowe (nominalne). Miary wprowadzone dla danych liczbowych, wykorzystujące wartości liczbowe, mają zastosowanie tylko dla nich. Miary dla zmiennych porządkowych nadają się również dla zmiennych liczbowych, ponieważ otrzymujemy je przez zamianę wartości cechy na kolejne liczby naturalne ![]() lub ułamki jednostajnie rozłożone na odcinku
lub ułamki jednostajnie rozłożone na odcinku ![]() , czyli
, czyli ![]() , gdzie
, gdzie ![]() . Miary dla zmiennych jakościowych są oparte na gęstościach i mają zastosowanie do wszystkich zmiennych.
. Miary dla zmiennych jakościowych są oparte na gęstościach i mają zastosowanie do wszystkich zmiennych.
Miary zależności i bliskości zostaną podzielone na symetryczne i niesymetryczne (zależność czy błąd nie muszą być relacjami symetrycznymi). Podsumowanie znajduje się w poniższej tabelce:
| Zmienne ilościowe | Zmienne porządkowe | Zmienne jakościowe | |
| Miary zależności | Korelacja | Korelacja rang, | Wspólna |
| symetryczne | Współczynnik Kendalla | Informacja | |
| Miary zależności | Współczynnik | ||
| niesymetryczne | Goodmana-Kruskala | ||
| Miary odległości | Błąd średniokwadratowy | ||
| symetryczne | |||
| Miary odległości |
|
||
| niesymetryczne |
W dalszej części skryptu będziemy oznaczać wielkimi literami, np. ![]() ,
, ![]() zarówno zmienne losowe jak i ich realizacje. Rozróżnienie będzie wynikać z kontekstu.
zarówno zmienne losowe jak i ich realizacje. Rozróżnienie będzie wynikać z kontekstu.
Definicja 1.1
Próbą będziemy nazywali ![]() realizacji zmiennej losowej:
realizacji zmiennej losowej: ![]() .
.
Średnią z próby będziemy oznaczać jako:
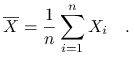 |
1.1. Zmienne ilościowe
Dla zmiennych ilościowych możemy zdefiniować kwantyle:
Definicja 1.2
Kwantyl rzędu ![]() ,
, ![]()
![]()
![]() :
:
gdzie ![]() oznacza dystrybuantę. Kwantyle rzędu
oznacza dystrybuantę. Kwantyle rzędu ![]() i
i ![]() nazywamy kwartylami, z czego kwantyl rzędu
nazywamy kwartylami, z czego kwantyl rzędu ![]() to mediana.
to mediana.
Estymatorami kwantyli dla próby ![]() są kwantyle próbkowe.
są kwantyle próbkowe.
Definicja 1.3
Kwantyle próbkowe rzędu ![]() dla próby n-elementowej,
dla próby n-elementowej, ![]()
![]()
![]() :
:
gdzie ![]() oznacza
oznacza ![]() -ty element statystyki pozycyjnej: po uszeregowaniu niemalejąco wartości
-ty element statystyki pozycyjnej: po uszeregowaniu niemalejąco wartości ![]() oznacza
oznacza ![]() -tą wartość z
-tą wartość z ![]() -elementowego ciągu. Funkcja ceiling zwraca najmniejszą liczbę całkowitą mniejszą od danej, a funkcja floor największą liczbę całkowitą mniejszą.
-elementowego ciągu. Funkcja ceiling zwraca najmniejszą liczbę całkowitą mniejszą od danej, a funkcja floor największą liczbę całkowitą mniejszą.
1.1.1. Miary rozrzutu
-
Wariancja:
wersja populacyjna
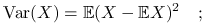
wersja próbkowa
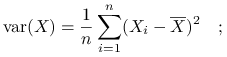
wersja próbkowa nieobciążona
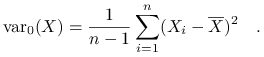
-
Odchylenie standardowe:
wersja populacyjna
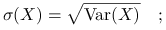
wersja próbkowa
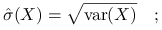
wersja próbkowa niebciążona
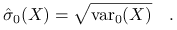
-
MAD (Median of Absolute Deviation):
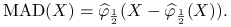
Dla rozkładu normalnego, MAD
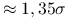 .
. -
IQR (Interquartile Range)
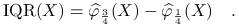
Dla rozkładu normalnego IQR
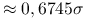 .
.
1.1.2. Miary zależności
-
Korelacja pomiędzy zmiennymi
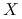 i
i 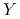 :
: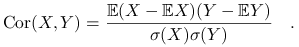
Dla próby
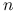 -elemnentowej:
-elemnentowej: 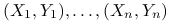 korelacja próbkowa:
korelacja próbkowa: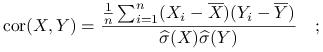
korelacja próbkowa nieobciążona:
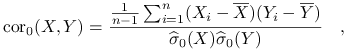
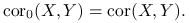
1.2. Zmienne porządkowe
Zmienne porządkowe to takie, dla których nie są ważne wartości, ale kolejność, w jakiej są ustawione. Z pojęciem zmiennej porządkowej ściśle wiąże się pojęcie rangi. Nadanie rang obserwacjom uniezależnia je od skali.
Definicja 1.4
Rangi dla obserwacji w próbie ![]() :
:
Przykład 1.1
Dla ![]() rangi są równe:
rangi są równe:
| X | 2 | 3 | 2,5 | 2,5 | 1,5 |
|---|---|---|---|---|---|
| R | 2 | 5 | 3,5 | 3,5 | 1 |
1.2.1. Miary zależności
-
Korelacja rang (Spearmana):
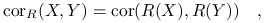
gdzie
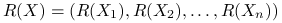 ,
, 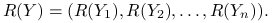
Stwierdzenie 1.1
Załóżmy, że ![]() mają rozkłady o ciągłych i ściśle rosnących dystrybuantach. Wtedy:
mają rozkłady o ciągłych i ściśle rosnących dystrybuantach. Wtedy:
-
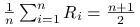 ;
; -
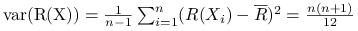 ;
;
-
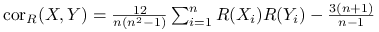 ;
; -
![\text{cor}_{R}(X,Y)\xrightarrow[n\rightarrow\infty]{p.n}\text{Cor}(F_{X}(X),F_{Y}(Y))](wyklady/st2/mi/mi129.png) ;
; -
Jeżeli
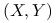 ma 2-wymiarowy rozkład normalny,
ma 2-wymiarowy rozkład normalny,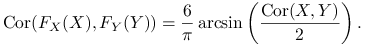
-
Współczynnik Kendala zależności między
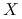 a
a 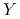 :
:Załóżmy, że
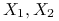 to zmienne losowe niezależne i o takim samym rozkładzie co
to zmienne losowe niezależne i o takim samym rozkładzie co 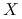 ,
, 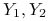 niezależne o takim samym rozkładzie co
niezależne o takim samym rozkładzie co 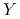 . Niech:
. Niech:![X_{{12}}=\left\{\begin{array}[]{ll}1,&\hbox{$X_{1}>X_{2}$ ;}\\
0,&\hbox{$X_{1}=X_{2}$ ;}\\
-1,&\hbox{$X_{1}<X_{2}$ .}\end{array}\right.\quad Y_{{12}}=\left\{\begin{array}[]{ll}1,&\hbox{$Y_{1}>Y_{2}$ ;}\\
0,&\hbox{$Y_{1}=Y_{2}$ ;}\\
-1,&\hbox{$Y_{1}<Y_{2}$ .}\end{array}\right.](wyklady/st2/mi/mi23.png)
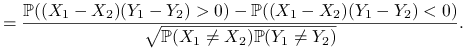 |
Jeśli ![]() mają ciągłe dystrybuanty, to
mają ciągłe dystrybuanty, to
Wersja próbkowa ![]() :
:
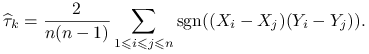 |
Uwaga 1.1
W programie R: cor(X, Y, method = c(”pearson”, ”kendall”, ”spearman”)) z domyślnie ustawioną opcją ”pearson”.
1.3. Zmienne jakościowe
W tej części omówione zostaną miary rozrzutu, zależności i bliskości oparte na gęstościach prawdopodobieństwa, wykorzystywane przede wszytkim do analizy cech jakościowych.
1.3.1. Miary rozrzutu
-
Entropia dla gęstości
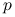 o nośniku
o nośniku 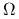 :
:![\text{H}(p)=-\int _{{\Omega}}[\ln p(v)]p(v)dv.](wyklady/st2/mi/mi84.png)
Jeśli
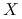 - zmienna losowa o gęstości
- zmienna losowa o gęstości 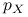 , to
, to 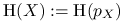 .
.
Uwaga 1.2
Różnice i podobieństwa między H![]() i Var
i Var![]() :
:
-
Załóżmy, że
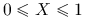 . Wtedy
. Wtedy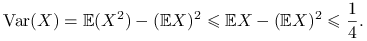
Zatem wariancja jest największa dla rozkładu dwupunktowego:
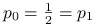 . Entropia natomiast jest największa dla rozkładu jednostajnego.
. Entropia natomiast jest największa dla rozkładu jednostajnego. -
Załóżmy teraz, że
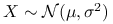 . Mamy:
. Mamy: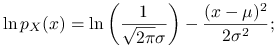
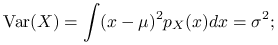
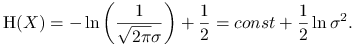
-
Współczynnik Giniego dla gęstości
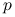 :
:![\text{V}(p)=\int _{{\Omega}}[1-p(v)]p(v)dv=1-\int _{{\Omega}}p^{2}(v)dv.](wyklady/st2/mi/mi69.png)
Jeśli
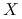 - zmienna losowa o gęstości
- zmienna losowa o gęstości 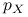 , to
, to 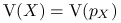 .
.V(p) jest liniowym (rozwinięcie Taylora dla logarytmu naturalnego:
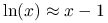 ) przybliżeniem H(p).
) przybliżeniem H(p).
1.3.2. Miary bliskości
Dla prostoty ograniczymy się w dalszej części wykładu do rozkładów dyskretnych zadanych gęstościami ![]() i
i ![]() o wspólnym nośniku
o wspólnym nośniku ![]() .
.
-
Odległość Kullbacka-Leiblera (względna entropia):
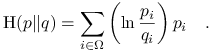
Stwierdzenie 1.2
Własności Odległości Kullbacka-Leiblera (entropii względnej):
-
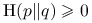 ;
; -
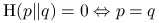 .
.
Skorzystajmy z nierówności: ![]() :
:
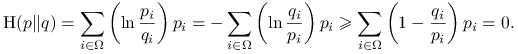 |
Stąd otrzymujemy ![]() Równość w ostatniej nierówności jest równoważna warunkowi
Równość w ostatniej nierówności jest równoważna warunkowi ![]() dla wszystkich
dla wszystkich ![]() , otrzymujemy
, otrzymujemy ![]()
-
Odległość
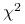 między rozkładami dyskretnymi zadanymi gęstościami
między rozkładami dyskretnymi zadanymi gęstościami 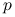 i
i 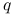 o wspólnym nośniku
o wspólnym nośniku 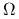 :
: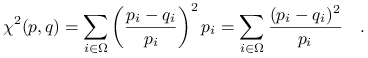
(1.1) Odległość
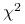 jest kwadratowym (rozwinięcie Taylora dla logarytmu:
jest kwadratowym (rozwinięcie Taylora dla logarytmu: 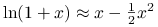 , gdzie za
, gdzie za  wstawiamy
wstawiamy 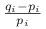 ) przybliżeniem
) przybliżeniem 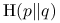 :
: 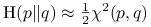 .
.
1.3.3. Miary zależności
Niech ![]() będą zmiennymi o rozkładzie dyskretnym, niekoniecznie o tym samym nośniku
będą zmiennymi o rozkładzie dyskretnym, niekoniecznie o tym samym nośniku ![]() . Ponadto zdefiniujmy:
. Ponadto zdefiniujmy:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
warunkowy współczynnik Giniego ![]() ;
;
warunkową entropię ![]() .
.
Zauważmy, że:
-
Współczynnik Goodmana-Kruskala (mówi on o tym, jak zmienił się rozrzut po zaobserwowaniu cechy
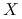 ):
):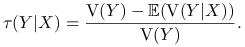
Zakładamy, że rozkład
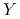 jest niezdegenerowany, czyli że
jest niezdegenerowany, czyli że 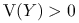 .
.
Stwierdzenie 1.3
Własności Współczynnika Goodmana-Kruskala:
-
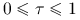 ;
; -
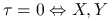 niezależne.
niezależne.
Oczywiście ![]() .
Dla dowodu, że
.
Dla dowodu, że ![]() zauważmy, że
zauważmy, że
![]() Wystarczy pokazać, że
Wystarczy pokazać, że ![]() .
Z kolei wystarczy pokazać, że
.
Z kolei wystarczy pokazać, że ![]() .
Lewa
.
Lewa![]() , więc
, więc ![]() wynika z nierówności Jensena.
wynika z nierówności Jensena.
Dla dowodu ![]() zauważmy, że ,,=” w nierówności Jensena wyrazów
zauważmy, że ,,=” w nierówności Jensena wyrazów ![]()
![]() jest równoważna niezależności
jest równoważna niezależności ![]() .
.
-
Wspólna informacja zawarta w
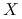 i
i 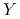 :
: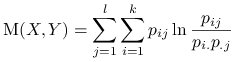
Stwierdzenie 1.4
Własności Wspólnej informacji:
-
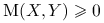 ;
; -
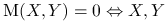 niezależne.
niezależne.
Wynika z własności odległości Kullbacka-Leiblera (stwierdzenie 1.2), bo ![]()
Uwaga 1.3
Korzystając z przybliżenia rozwinięciem w szereg Taylora logarytmu: ![]() , otrzymujemy:
, otrzymujemy:
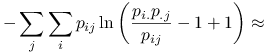 |
|||
![\displaystyle-\left[\sum _{{ji}}\left(\frac{p_{{i.}}p_{{.j}}}{p_{{ij}}}-1\right)p_{{ij}}-\frac{1}{2}\sum _{{ji}}\left(\frac{p_{{i.}}p_{{.j}}}{p_{{ij}}}-1\right)^{2}p_{{ij}}\right]=](wyklady/st2/mi/mi155.png) |
|||
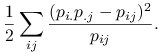 |
Ostatnie wyrażenie oraz statystyka ![]() dla testowania niezależności mają podobną interpretację, chociaż różnica w treści matematycznej jest zasadnicza. Być może o podobieństwie wyrażeń decydują własności błędu względnego: jeśli błąd względny oszacowania
dla testowania niezależności mają podobną interpretację, chociaż różnica w treści matematycznej jest zasadnicza. Być może o podobieństwie wyrażeń decydują własności błędu względnego: jeśli błąd względny oszacowania ![]() za pomocą
za pomocą ![]() jest nie większy od
jest nie większy od ![]() , to błąd względny oszacowania
, to błąd względny oszacowania ![]() za pomocą
za pomocą ![]() jest nie większy niż
jest nie większy niż ![]() . Przy małym
. Przy małym ![]() wyrażenia te są porównywalne.
wyrażenia te są porównywalne.
Uwaga 1.4
Wspólna informacja dla rozkładu dwuwymiarowego normalnego, gdzie ![]() ,
jest równa:
,
jest równa:
gdzie ![]() .
.
-
Jeżeli zamiast współczynnika Giniego we wzorze na współczynnik Goodmana-Kruskala użyjemy entropii, otrzymamy analogiczny współczynnik
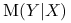 :
: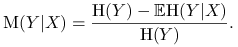
Stwierdzenie 1.5
![\displaystyle=-\left[\sum _{{ij}}p_{{ij}}\ln p_{{ij}}-\sum _{{ij}}p_{{ij}}\ln p_{{i.}}\right]=](wyklady/st2/mi/mi139.png) |
|||
gdzie ![]() .
.
Zatem ![]() .
.
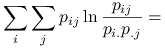 |
|||
Zatem ![]() . Stąd
. Stąd ![]() .
.
1.4. Przykłady w programie R
Obliczanie spółczynnika Goodmana-Kruskala: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/tauGK.R




