Zagadnienia

4.1 Metody skalowania danych
4.2 Własności
4.3 Przykłady w programie R

4. Skalowanie wielowymiarowe

Skalowanie wielowymiarowe pozwala na redukcję wymiaru cech. Dla macierzy danych:

$X=\left(\begin{array}[]{c}X_{1}^{T}\\ X_{2}^{T}\\ \ldots\\ X_{n}^{T}\\ \end{array}\right)_{{n\times p}}$

będziemy chcieli zrzutować ,,optymalnie” dane na $\mathbb{R}^{k}$ , czyli zmniejszyć macierz $X$ do $\hat{Z}$ o wymiarch $n\times k$ , $k<p$ .

Optymalność zdefiniujemy w kategoriach macierzy odległości lub podobieństwa dla $n$ obiektów. Zadaniem będzie znalezienie optymalnej reprezentacji obiektów w $\mathbb{R}^{k}$ .

Definicja 4.1

Macierz odległości to taka macierz, która spełnia własności:

$D=(d_{{ij}})_{{i,j=1}}^{n},\quad d_{{ij}}\geq 0,\quad d_{{ij}}=d_{{ji}},\quad d_{{ii}}=0.$

Macierz podobieństwa jest macierzą konstruowaną w sposób przeciwstawny do macierzy odległości o własnościach:

$C=(c_{{ij}})_{{i,j=1}}^{n},\quad c_{{ij}}=c_{{ji}},\quad c_{{ii}}\geq c_{{ij}}\text{ }\forall i,j.$

4.1. Metody skalowania danych

Dla macierzy danych $X$ o wymiarach $n\times p$ , zdefiniujmy $D$ jako macierz odległości euklidesowych pomiędzy obiektami:

$d_{{ij}}^{2}=||X_{i}-X_{j}||^{2}.$

Classical multidimensional scaling:

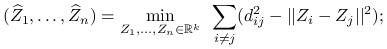
$(\widehat{Z}_{1},\ldots,\widehat{Z}_{n})=\min _{{Z_{1},\ldots,Z_{n}\in\mathbb{R}^{k}}}\text{ }\sum _{{i\neq j}}(d_{{ij}}^{2}-||Z_{i}-Z_{j}||^{2});$
Sammon scaling:

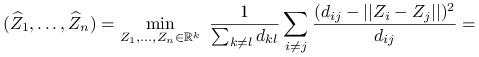
$(\widehat{Z}_{1},\ldots,\widehat{Z}_{n})=\min _{{Z_{1},\ldots,Z_{n}\in\mathbb{R}^{k}}}\text{ }\frac{1}{\sum _{{k\neq l}}d_{{kl}}}\sum _{{i\neq j}}\frac{(d_{{ij}}-||Z_{i}-Z_{j}||)^{2}}{d_{{ij}}}=$

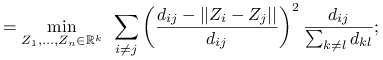
$=\min _{{Z_{1},\ldots,Z_{n}\in\mathbb{R}^{k}}}\text{ }\sum _{{i\neq j}}\left(\frac{d_{{ij}}-||Z_{i}-Z_{j}||}{d_{{ij}}}\right)^{2}\frac{d_{{ij}}}{\sum _{{k\neq l}}d_{{kl}}};$
Kruskal-Shepard scaling:

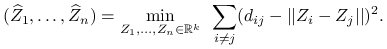
$(\widehat{Z}_{1},\ldots,\widehat{Z}_{n})=\min _{{Z_{1},\ldots,Z_{n}\in\mathbb{R}^{k}}}\text{ }\sum _{{i\neq j}}(d_{{ij}}-||Z_{i}-Z_{j}||)^{2}.$

4.2. Własności

Niech $L$ oznacza macierz ortogonalną $p\times p$ , $L=(L_{1},L_{2})$ , $L_{1}$ o wymiarze $p\times k$ . Oznaczmy $\widehat{Z}=XL_{1}$ , czyli rzut $X$ na $\mathbb{R}^{k}$ . Zdefiniujmy macierz odległości dla $\widehat{Z}$ jako $\widehat{D}=(\widehat{d}_{{rs}})$ . Zauważmy, że:

$d_{{rs}}^{2}=||X_{r}-X_{s}||^{2}=||L^{T}(X_{r}-X_{s})||^{2},$

ponieważ mnożenie wektora przez macierz ortogonalną nie zmienia jego normy. Mamy więc:

$d_{{rs}}^{2}=\sum _{{j=1}}^{p}(X_{{rj}}-X_{{sj}})^{2}=\sum _{{j=1}}^{p}[l_{j}^{T}(X_{{r}}-X_{{s}})]^{2}\geq\sum _{{j=1}}^{k}[l_{j}^{T}(X_{{r}}-X_{{s}})]^{2}=\widehat{d}_{{rs}}^{2}.$

Stwierdzenie 4.1

Rzut $X$ na $k$ pierwszych składowych głównych minimalizuje wyrażenie $\sum _{{r\neq s}}(d_{{rs}}^{2}-\widehat{d}_{{rs}}^{2})$ wśród wszystkich rzutów $XL_{1}$ . Jest więc rozwiązaniem zadania classical multidimensional scaling.

Przyjrzyjmy się następującej macierzy:

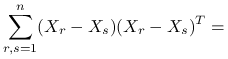$\sum _{{r,s=1}}^{n}(X_{r}-X_{s})(X_{r}-X_{s})^{T}=$

dla $\overline{X}=\frac{1}{n}\sum _{{i=1}}^{n}X_{i}$ ,

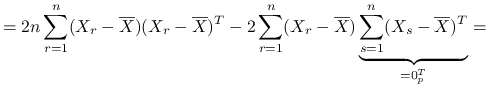$=2n\sum _{{r=1}}^{n}(X_{r}-\overline{X})(X_{r}-\overline{X})^{T}-2\sum _{{r=1}}^{n}(X_{r}-\overline{X})\underbrace{\sum _{{s=1}}^{n}(X_{s}-\overline{X})^{T}}_{{=0_{p}^{T}}}=$

$=2n\text{ }\left(\begin{array}[]{ccc}\sum _{{r=1}}^{n}(X_{{r1}}-\overline{X}_{{.1}})^{2}&\ldots&\sum _{{r=1}}^{n}(X_{{r1}}-\overline{X}_{{.1}})(X_{{rp}}-\overline{X}_{{.p}})\\ \ldots&\ldots&\ldots\\ \sum _{{r=1}}^{n}(X_{{rp}}-\overline{X}_{{.p}})(X_{{r1}}-\overline{X}_{{.1}})&\ldots&\sum _{{r=1}}^{n}(X_{{rp}}-\overline{X}_{{.p}})^{2}\\ \end{array}\right)+0=$

$=2nnS,$

gdzie $S$ jest macierzą kowariancji próbkowej (estymator obciążony).

Wróćmy do minimalizacji wyrażenia:

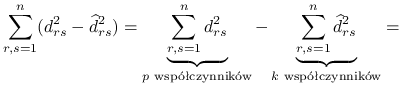$\sum _{{r,s=1}}^{n}(d_{{rs}}^{2}-\widehat{d}_{{rs}}^{2})=\underbrace{\sum _{{r,s=1}}^{n}d_{{rs}}^{2}}_{{p\text{ współczynników}}}-\underbrace{\sum _{{r,s=1}}^{n}\widehat{d}_{{rs}}^{2}}_{{k\text{ współczynników}}}=$

$=\underbrace{\sum _{{r,s=1}}^{n}\sum _{{j=k+1}}^{p}[l_{j}^{T}(X_{r}-X_{s})]^{2}}_{{\text{zostaje }p-k\text{ współczynników}}}.$

Ponieważ $\sum _{{r,s=1}}^{n}d_{{rs}}^{2}$ jest stałą, zadanie minimalizacji wyrażenia $\sum _{{r,s=1}}^{n}(d_{{rs}}^{2}-\widehat{d}_{{rs}}^{2})$ jest równoważne zadaniu maksymalizacji $\sum _{{r,s=1}}^{n}\widehat{d}_{{rs}}^{2}$ . Maksymalizujemy po ortogonalnym układzie wektorów $l_{1},\ldots,l_{k}$ wyrażenie:

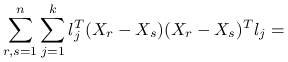$\sum _{{r,s=1}}^{n}\sum _{{j=1}}^{k}l_{j}^{T}(X_{r}-X_{s})(X_{r}-X_{s})^{T}l_{j}=$

$=\sum _{{j=1}}^{k}l_{j}^{T}\left[\sum _{{r,s=1}}^{n}(X_{r}-X_{s})(X_{r}-X_{s})^{T}\right]l_{j}=$

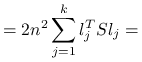$=2n^{2}\sum _{{j=1}}^{k}l_{j}^{T}Sl_{j}=$

korzystając z rozkładu spektralnego $S$ ,

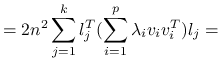$=2n^{2}\sum _{{j=1}}^{k}l_{j}^{T}(\sum _{{i=1}}^{p}\lambda _{i}v_{i}v_{i}^{T})l_{j}=$

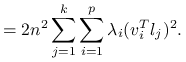$=2n^{2}\sum _{{j=1}}^{k}\sum _{{i=1}}^{p}\lambda _{i}(v_{i}^{T}l_{j})^{2}.$

Dalszy dowód przebiega analogicznie do dowodu stwierdzenia 3.6. Można zauważyć związek pomiędzy własnościami składowych głównych dla podejścia populacyjnego i próbkowego.

∎

4.3. Przykłady w programie R

Skalowanie wielowymiarowe:

porównanie skalowania wielowymiarowego i analizy składowych głównych dla danych Kraby: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/mds.R
porównanie skalowania wielowymiarowego i analizy składowych głównych dla danych Iris i Kraby: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/rzutDanych.R

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Statystyka II wykłady