Zagadnienia
6. Klasteryzacja
Klasteryzacja jest, podobnie jak analiza składowych głównych, metodą redukcji wymiaru danych. W tym przypadku jednak redukcja będzie się odbywać w pionie a zamiast odcinania części danych, będziemy je grupować. Nowym wymiarem danych będzie liczba grup. Dla macierzy ![]() będziemy szukać optymalnego podziału na
będziemy szukać optymalnego podziału na ![]() części, czyli szukać podziału
części, czyli szukać podziału ![]() na
na ![]() grup:
grup:
parami rozłącznych o licznościach odpowiednio ![]() . Będziemy używać oznaczenia
. Będziemy używać oznaczenia ![]() na podmacierz
na podmacierz ![]() o indeksach z
o indeksach z ![]() ,
, ![]()
6.1. Klasteryzacja  -średnich
-średnich
Klasteryzacji ![]() -średnich używamy, gdy znamy ilość grup
-średnich używamy, gdy znamy ilość grup ![]() , na ile chcemy podzielić dane. Zdefiniujmy następujące macierze:
, na ile chcemy podzielić dane. Zdefiniujmy następujące macierze:
Macierz wariancji całkowitej:
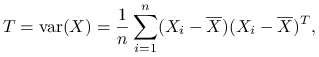 |
nie zależy od podziału ![]() , var oznacza próbkową macierz kowariancji.
, var oznacza próbkową macierz kowariancji.
Zmienność całkowita to ślad macierzy T: ![]() .
.
Macierz wariancji wewnątrzgrupowej:
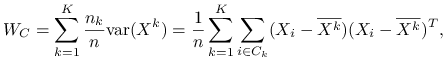 |
zależy od podziału ![]() .
.
Zmienność wewnątrzgrupowa to ślad macierzy ![]() :
: ![]() .
.
Macierz wariancji międzygrupowej:
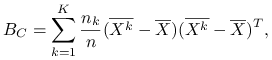 |
zależy od podziału ![]() .
.
Zmienność międzygrupowa to ślad macierzy ![]() :
: ![]() .
.
![]() oznacza
oznacza ![]() -wymiarowy wektor średnich kolumnowych dla macierzy
-wymiarowy wektor średnich kolumnowych dla macierzy ![]() , a
, a ![]()
![]() -wymiarowy wektor średnich kolumnowych dla całej macierzy
-wymiarowy wektor średnich kolumnowych dla całej macierzy ![]() .
. ![]() nazywane są centroidami, redukcja wymiaru polega na zastępowaniu grup danych przez ich centroidy.
nazywane są centroidami, redukcja wymiaru polega na zastępowaniu grup danych przez ich centroidy.
Stwierdzenie 6.1
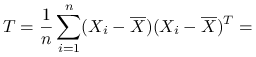 |
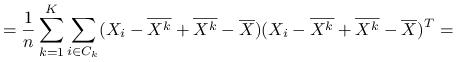 |
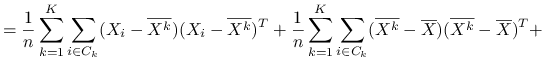 |
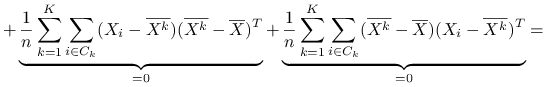 |
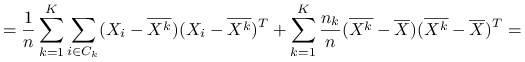 |
Wniosek 6.1
Czyli
Ideą klasteryzacji ![]() -średnich jest minimalizacja po podziałach zmienności wewnątrzgrupowej, co jest jednoznaczne z maksymalizcją zmienności międzygrupowej:
-średnich jest minimalizacja po podziałach zmienności wewnątrzgrupowej, co jest jednoznaczne z maksymalizcją zmienności międzygrupowej:
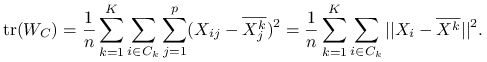 |
Idea zachłannego algorytmu ![]() -średnich (zależnego od wybranego podziału startowego
-średnich (zależnego od wybranego podziału startowego ![]() ), z którego można korzystać np. w programie
), z którego można korzystać np. w programie ![]() wygląda następująco:
wygląda następująco:
Algorytm  -średnich
-średnich
| Wielokrotnie powtarzamy przy różnym podziale startowym |
| repeat |
| for ( |
| |
| for ( |
| |
| until warunek stopu |
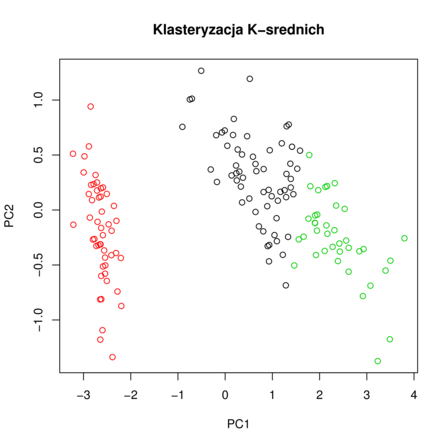
Przykładowy wynik algorytmu klasteryzacji ![]() -średnich znajduje się na rysunku 6.1.
-średnich znajduje się na rysunku 6.1.
6.2. Klasteryzacja  -medoidów
-medoidów
Klasteryzacja ![]() -medoidów jest podobna do klasteryzacji
-medoidów jest podobna do klasteryzacji ![]() -średnich, z tą różnicą, że zamiast średnich arytmetycznych w algorytmie będziemy używać median. Dzięki takiemu sformułowaniu, możemy go używać przy dowolnej macierzy odległości między obiektami
-średnich, z tą różnicą, że zamiast średnich arytmetycznych w algorytmie będziemy używać median. Dzięki takiemu sformułowaniu, możemy go używać przy dowolnej macierzy odległości między obiektami ![]() .
.
Algorytm  -medoidów
-medoidów
| Wielokrotnie powtarzamy przy różnym podziale startowym |
| repeat |
| for ( |
| |
| for ( |
| |
| until warunek stopu |
6.3. Klasteryzacja hierarchiczna
Używając klasteryzacji hierarchicznej nie zakładamy z góry ilości klastrów, na jakie chcemy podzielić dane. Wychodzimy od sytuacji, gdy mamy ![]() klastrów, czyli każda obserwacja jest oddzielną grupą. W każdym kroku algorytmu łączymy 2 klastry, czyli zmniejszamy ich liczbę o jeden i tak aż do połączenia wszystkich obserwacji w jedną grupę. Wybór ilości klastrów opieramy na wykresie separowalności, która obliczana jest dla każdego kroku algorytmu.
klastrów, czyli każda obserwacja jest oddzielną grupą. W każdym kroku algorytmu łączymy 2 klastry, czyli zmniejszamy ich liczbę o jeden i tak aż do połączenia wszystkich obserwacji w jedną grupę. Wybór ilości klastrów opieramy na wykresie separowalności, która obliczana jest dla każdego kroku algorytmu.
W klasteryzacji hierarchicznej możemy używać różnych metod aglomeracji danych.
Dla macierzy odległości ![]() odległość dwóch klastrów
odległość dwóch klastrów ![]() i
i ![]() od siebie przy założeniach
od siebie przy założeniach
możemy zdefiniować jako:
-
Single linkage
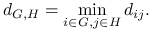
-
Average linkage
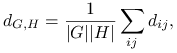
gdzie
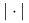 oznacza liczność zbioru.
oznacza liczność zbioru. -
Complete linkage
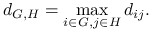
Ideę algorytmu klasteryzacji hierarchicznej możemy zapisać jako:
Algorytm klasteryzacji hierarchicznej
| |
| for (l in 1:(n-1)) |
| połącz najbliższe dwa klastry: |
| |
| klastry |
| odnów macierz odległości |
Definicja 6.1
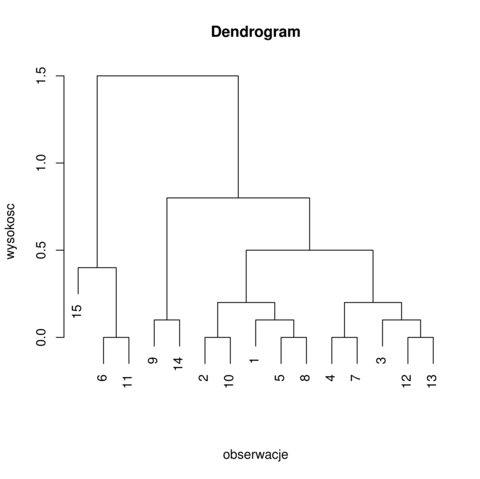
Dendrogram jest metodą ilustracji wyników klasteryzacji hierarchicznej. Możemy obserwować od dołu dendrogramu (rysunek 6.2) jak kolejne klastry się łączą i dla jakiej wysokości (odległości klastrów) to zachodzi.
Definicja 6.2
Oznaczmy ![]() jako minimalną wysokość, na której obserwujemy podział na
jako minimalną wysokość, na której obserwujemy podział na ![]() części. Na przykład, na obrazku 6.2 dla
części. Na przykład, na obrazku 6.2 dla ![]()
![]() .
.
Separowalność dla klasteryzacji hierarchicznej definiujemy jako:
Z definicji separowalności możemy wywnioskować następujące własności:
-
separowalność przyjmuje wartości z przedziału
![[0,1]](wyklady/st2/mi/mi164.png) ;
; -
jest niemalejącą funkcją liczby klastrów.
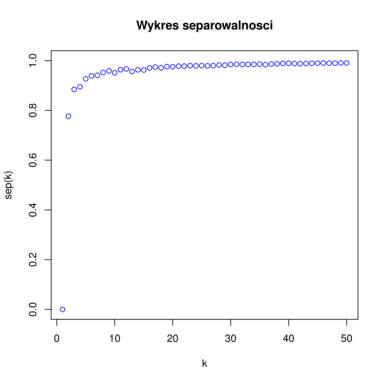
Przykładowy wykres separowalności znajduje się na rysunku 6.3. Na podstawie tego wykresu podejmuje się decyzję dotyczącą optymalnej ilości klastrów. Szukamy takiego ![]() , żeby
, żeby ![]() było duże w stosunku do
było duże w stosunku do ![]() . Chcemy znaleźć taką niewielką liczbę klastrów, żeby zysk mierzony separowalnością przy łączeniu klastrów w danym kroku był duży, a dalsze sklejanie grup nie dawało już takich korzyści. Graficznie sprowadza się to do szukania ,,kolanka” funkcji separowlaności. Jednym ze sposobów jest szukanie punktu na wykresie najbliższego punktowi
. Chcemy znaleźć taką niewielką liczbę klastrów, żeby zysk mierzony separowalnością przy łączeniu klastrów w danym kroku był duży, a dalsze sklejanie grup nie dawało już takich korzyści. Graficznie sprowadza się to do szukania ,,kolanka” funkcji separowlaności. Jednym ze sposobów jest szukanie punktu na wykresie najbliższego punktowi ![]() . Przykładowo, na rysunku 6.3 optymalnym wyborem jest
. Przykładowo, na rysunku 6.3 optymalnym wyborem jest ![]() (
(![]() też jest dobrym wyborem, chociaż dążymy do tego aby jak najbardziej zredukować wymiar danych, czyli wybrać jak najmniejsze
też jest dobrym wyborem, chociaż dążymy do tego aby jak najbardziej zredukować wymiar danych, czyli wybrać jak najmniejsze ![]() ).
).
Definicja 6.3
Można zdefiniować także separowalność dla klasteryzacji ![]() -średnich. Oznaczmy:
-średnich. Oznaczmy:
Ponieważ wiemy, że:
możemy zdefiniować separowalność jako:
Stwierdzenie 6.2
Separowalność dla klasteryzacji ![]() -średnich jest niemalejącą funkcją
-średnich jest niemalejącą funkcją ![]() , liczby klastrów. Funkcja
, liczby klastrów. Funkcja ![]() jest więc nierosnąca ze względu na liczbę klastrów.
jest więc nierosnąca ze względu na liczbę klastrów.
Jako praca domowa.
∎6.4. Przykłady w programie R
Klasteryzacja:
-
k-średnich i hierarchiczna na danych Kraby, kobiety Pima i Irysy: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/ileKlastrow.R
-
wybór liczby klastrów na podstawie wykresu separowalności i sylwetki dla algorytmów k-średnich i k-medoidów: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/sep_syl.r
-
k-średnich i hierarchiczna zobrazowane przy pomocy analizy składowych głównych: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/pca.R
-
k-średnich i hierarchiczna oraz PCA i skalowanie wielowymiarowe dla danych Iris i Kraby: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/rzutDanych.R