Zagadnienia
7. Klasyfikacja
Zadanie klasyfikacji polega na konstrukcji funkcji (klasyfikatora), która na podstawie zaobserwowanych cech będzie przydzielała obserwację do którejś z wcześniej zdefiniowanych grup. Do estymacji funkcji potrzebne są obserwacje, które już zostały sklasyfikowane, będziemy je nazywać próbą uczącą:
Dane ![]() oznaczają zaobserwowane cechy,
oznaczają zaobserwowane cechy, ![]() grupę, do której obserwacja została zaklasyfikowana.
grupę, do której obserwacja została zaklasyfikowana.
![]() oznaczaja zbiór tych indeksów
oznaczaja zbiór tych indeksów ![]() , że
, że ![]() ;
; ![]() są rozłączne o licznościach odpowiednio
są rozłączne o licznościach odpowiednio ![]()
Funkcja wiarygodności dla opisanych danych wyraża się wzorem:
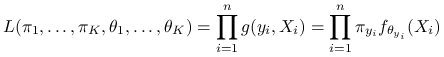 |
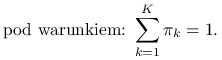 |
Logwiarygodność to logarytm funkcji wiarygodności:
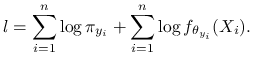 |
Zadanie klasyfikacji dzielimy na dwa kroki:
-
Estymujemy parametry
 oraz
oraz 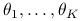 na podstawie zaobserwowanych par
na podstawie zaobserwowanych par 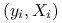 przy użyciu metody największej wiarygodności. Parametry
przy użyciu metody największej wiarygodności. Parametry 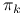 możemy interpretować jako prawdopodobieństwa przynależności do danej grupy danych, a
możemy interpretować jako prawdopodobieństwa przynależności do danej grupy danych, a 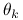 jako parametry rozkładu w danej grupie (na przykład dla wielowymiarowego rozkładu normalnego, byłyby to średnia
jako parametry rozkładu w danej grupie (na przykład dla wielowymiarowego rozkładu normalnego, byłyby to średnia 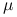 i macierz kowariancji
i macierz kowariancji 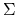 ).
). -
Obserwujemy nowe cechy
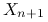 i przyporządkowujemy im
i przyporządkowujemy im 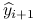 na podstawie zbudowanego przez nas klasyfikatora. Będziemy go także nazywać regułą decyzyjną.
na podstawie zbudowanego przez nas klasyfikatora. Będziemy go także nazywać regułą decyzyjną.
Maksymalizujemy funkcję wiarygodności pod warunkiem ![]() przy użyciu metody mnożników Lagrange'a:
przy użyciu metody mnożników Lagrange'a:
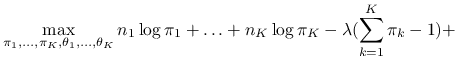 |
Liczymy estymatory ![]() :
:
| (7.1) |
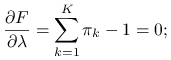 |
(7.2) |
Z równań 7.1 otrzymujemy:
Sumujemy po ![]() korzystając z równania 7.2 :
korzystając z równania 7.2 :
Estymację parametrów ![]() odłożymy do dalszej części wykładu.
odłożymy do dalszej części wykładu.
7.1. Optymalna reguła decyzyjna
Zobaczmy teraz, jak można zdefiniować optymalny klasyfikator w zależności od funkcji straty karzącej za błędne sklasyfikowanie danych.
Definicja 7.1
Funkcja straty to funkcja przyporządkowująca nieujemną wielkość kary poprzez porównanie prawdy (założymy chwilowo, że ją znamy) do podjętej decyzji (wyliczonego estymatora):
Przykładową funkcją kary dla ciągłego ![]() jest
jest ![]() .
.
Mając wyestymowaną regułę decyzyjną sensownym jest rozpatrywanie średniej straty dla naszego klasyfikatora:
Definicja 7.2
Ryzyko reguły decyzyjnej dla ![]() :
:
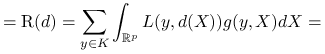 |
gdzie ![]() jest gęstością łącznego rozkładu danych. Z twierdzenia o prawdopodobieństwie całkowitym:
jest gęstością łącznego rozkładu danych. Z twierdzenia o prawdopodobieństwie całkowitym:
![=\sum _{{k=1}}^{K}\left[\int _{{\mathbb{R}^{p}}}L(k,d(X))f(X|k)dX\right]\pi _{k}.](wyklady/st2/mi/mi566.png) |
Definicja 7.3
Optymalna reguła decyzyjna ![]() to taka reguła decyzyjna, że
to taka reguła decyzyjna, że
Definicja 7.4
Reguła bayesowska ![]() to reguła decyzyjna, która lokalnie dla danego
to reguła decyzyjna, która lokalnie dla danego ![]() spełnia warunek:
spełnia warunek:
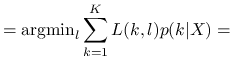 |
ze wzoru Bayesa:
![=\text{argmin}_{l}\left[\sum _{{k=1}}^{K}L(k,l)\frac{\pi _{k}f(X|k)}{\sum _{{s=1}}^{K}\pi _{s}f(X|s)}\right]=](wyklady/st2/mi/mi609.png) |
![=\text{argmin}_{l}\left[\sum _{{k=1}}^{K}L(k,l)\pi _{k}f(X|k)\right].](wyklady/st2/mi/mi563.png) |
Stwierdzenie 7.1
Reguła bayesowska jest optymalną regułą decyzyjną.
Dla dowolnej reguły decyzyjnej ![]() zachodzi:
zachodzi:
![\text{R}(d)=\sum _{{k=1}}^{K}\left[\int _{{\mathbb{R}^{p}}}L(k,d(X))f(X|k)dX\right]\pi _{k}=](wyklady/st2/mi/mi637.png) |
![=\int _{{\mathbb{R}^{p}}}\left[\sum _{{k=1}}^{K}L(k,d(X))\pi _{k}f(X|k)\right]dX\geq](wyklady/st2/mi/mi612.png) |
![\geq\int _{{\mathbb{R}^{p}}}\left[\min _{{1\leq l\leq k}}\sum _{{k=1}}^{K}L(k,l)\pi _{k}f(X|k)\right]dX=](wyklady/st2/mi/mi568.png) |
![=\int _{{\mathbb{R}^{p}}}\left[\sum _{{k=1}}^{K}L(k,d_{B}(X))\pi _{k}f(X|k)\right]dX=\text{R}(d_{B}).](wyklady/st2/mi/mi580.png) |
7.2. Wielowymiarowy rozkład normalny
W dalszej części wykładu będziemy zakładać, że ![]() mają rozkłady normalne. Dlatego przyjrzyjmy się bliżej własnościom wielowymiarowego rozkładu normalnego i estymacji jego parametrów metodą najwiękzej wiarygodności.
mają rozkłady normalne. Dlatego przyjrzyjmy się bliżej własnościom wielowymiarowego rozkładu normalnego i estymacji jego parametrów metodą najwiękzej wiarygodności.
Definicja 7.5
Wektor losowy ![]() ma rozkład wielowymiarowy normalny w
ma rozkład wielowymiarowy normalny w ![]() jeśli
jeśli ![]()
![]()
![]() ma rozkład normalny w
ma rozkład normalny w ![]() . Oznaczmy ten rozkład poprzez
. Oznaczmy ten rozkład poprzez ![]() , gdzie
, gdzie ![]() ,
, ![]() .
.
Twierdzenie 7.1
Jeżeli ![]() ma rokład normalny w
ma rokład normalny w ![]() , to
, to ![]()
![]() i macierzy
i macierzy ![]() wymiaru
wymiaru ![]() ,
, ![]() ma rozkład normalny w
ma rozkład normalny w ![]() .
.
Wniosek 7.1
Rozkłady brzegowe wielowymiarowego rozkładu normalnego są normalne w odpowiednich podprzestrzeniach ![]() .
.
Twierdzenie 7.2
Fcja charakterystyczna zmiennej losowej ![]() o rozkładzie normalnym w
o rozkładzie normalnym w ![]() jest postaci:
jest postaci:
| (7.3) |
Także na odwrót: jeżeli ![]() jest symetryczną macierzą dodatnio określoną o wymiarach
jest symetryczną macierzą dodatnio określoną o wymiarach ![]() , to
, to ![]() określona w równaniu 7.3 jest funkcją charakterystyczną wektora losowego o rozkładzie normalnym w
określona w równaniu 7.3 jest funkcją charakterystyczną wektora losowego o rozkładzie normalnym w ![]() .
.
Wniosek 7.2
Dowolna macierz symetryczna dodatnio określona o wymiarach ![]() jest macierzą kowariancji wektora losowego o rokładzie normalnym w
jest macierzą kowariancji wektora losowego o rokładzie normalnym w ![]() .
.
Twierdzenie 7.3
Gęstość wielowymiarowego rozkładu normalnego ![]() :
:
![f(X)=\frac{1}{(2\pi)^{{\frac{p}{2}}}(\underbrace{\text{det}(\Sigma)}_{{=|\Sigma|}})^{{\frac{1}{2}}}}\exp\left[-\frac{1}{2}(X-\mu)^{T}\Sigma^{{-1}}(X-\mu)\right].](wyklady/st2/mi/mi539.png) |
Twierdzenie 7.4
Jeżeli ![]() ma rozkład normalny w
ma rozkład normalny w ![]() :
: ![]() , to współrzędne wektora
, to współrzędne wektora ![]() są niezależne
są niezależne ![]()
![]() jest diagonalna. Dla rozkładu normalnego brak korelacji oznacza niezależność.
jest diagonalna. Dla rozkładu normalnego brak korelacji oznacza niezależność.
Twierdzenie 7.5
Jeżeli ![]() ,
, ![]() jest macierzą ortonormalną o wymiarach
jest macierzą ortonormalną o wymiarach ![]() , to:
, to:
7.2.1. Estymatory największej wiarygodności dla rozkładu normalnego 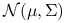
Niech ![]() będą niezależnymi wektorami losowymi z
będą niezależnymi wektorami losowymi z ![]() -wymiarowego rozkładu
-wymiarowego rozkładu ![]() . Znajdziemy estymatory dla parametrów
. Znajdziemy estymatory dla parametrów ![]() i
i ![]() . Łączna funkcja wiarygodności dla
. Łączna funkcja wiarygodności dla ![]() wektorów losowych:
wektorów losowych:
![L(\mu,\Sigma)=\prod _{{i=1}}^{n}\frac{1}{(2\pi)^{{\frac{p}{2}}}|\Sigma|^{{\frac{1}{2}}}}\exp\left[-\frac{1}{2}(X_{i}-\mu)^{T}\Sigma^{{-1}}(X_{i}-\mu)\right].](wyklady/st2/mi/mi633.png) |
Najpierw szukamy estymatora ![]() ; w tym celu opuszczamy wszystkie wyrazy nie zalezeżące od
; w tym celu opuszczamy wszystkie wyrazy nie zalezeżące od ![]() , które by się wyzerowały po policzeniu pochodnej. Dla prostoty obliczeń maksymalizujemy podwojoną logwiarygodność:
, które by się wyzerowały po policzeniu pochodnej. Dla prostoty obliczeń maksymalizujemy podwojoną logwiarygodność:
gdzie ![]() .
.
Przypomnijmy fakt:
Lemat 7.1
Oznaczmy: ![]() – wektory tej samej długości p,
– wektory tej samej długości p, ![]() macierz o wymiarach
macierz o wymiarach ![]() .
.
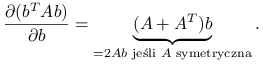 |
Skorzystajmy z lematu 7.1 żeby obliczyć pochodną logwiarygodności:
stąd
czyli estymatorem największej wiarygodności dla średniej rozkładu normalnego jest średnia arytmetyczna obserwacji.
Ponieważ optymalne ![]() nie zależy od
nie zależy od ![]() , przy obliczaniu
, przy obliczaniu ![]() możemy wstawić
możemy wstawić ![]() za
za ![]() . Maksymalizujemy po
. Maksymalizujemy po ![]() wyrażenie:
wyrażenie:
![L(\overline{X},\Sigma)\propto|\Sigma|^{{-\frac{n}{2}}}\exp\left[-\frac{1}{2}\sum _{{i=1}}^{n}(X_{i}-\overline{X})^{T}\Sigma^{{-1}}(X_{i}-\overline{X}).\right]](wyklady/st2/mi/mi582.png) |
Symbol ![]() oznacza proporcjonalność, możemy opuścić wszystkie stałe, które nie wpływają na wynik optymalizacji.
oznacza proporcjonalność, możemy opuścić wszystkie stałe, które nie wpływają na wynik optymalizacji.
Ponieważ (![]() jest liczbą, a
jest liczbą, a ![]() , oraz
, oraz ![]() , otrzymujemy:
, otrzymujemy:
![L(\overline{X},\Sigma)\propto|\Sigma|^{{-\frac{n}{2}}}\exp\left[-\frac{1}{2}\sum _{{i=1}}^{n}\text{tr}\{(X_{i}-\overline{X})(X_{i}-\overline{X})^{T}\Sigma^{{-1}}\}\right]=](wyklady/st2/mi/mi634.png) |
ślad macierzy jest funkcją liniową argumentu, więc zachodzi:
![=|\Sigma|^{{-\frac{n}{2}}}\exp\left[-\frac{1}{2}\text{tr}\{\underbrace{(X_{i}-\overline{X})(X_{i}-\overline{X})^{T}}_{{=S}}\Sigma^{{-1}}\}\right]=](wyklady/st2/mi/mi596.png) |
pomnóżmy i podzielmy przez ![]()
Ponieważ ![]() nie zależy od
nie zależy od ![]() , możemy to wyrażenie opuścić. Podstawmy
, możemy to wyrażenie opuścić. Podstawmy ![]() :
:
Lemat 7.2
Dla macierzy kwadratowej ![]() o wymiarach
o wymiarach ![]() zachodzi:
zachodzi:
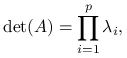 |
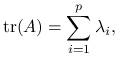 |
gdzie ![]() to wartości własne macierzy.
to wartości własne macierzy.
Korzystając z lematu 7.2:
![|B|^{{\frac{n}{2}}}\exp\left[-\frac{1}{2}\text{tr}B\right]=\prod _{{j=1}}^{p}\lambda _{j}^{{\frac{n}{2}}}e^{{-\frac{1}{2}\lambda _{j}}}](wyklady/st2/mi/mi590.png) |
Zmaksymalizujmy to wyrażenie po każdej wartości własnej ![]() , co sprowadza się do maksymalizacji po
, co sprowadza się do maksymalizacji po ![]() funkcji:
funkcji:
skąd ![]() .
.
Macierzą o wszystkich wartościach własnych równych ![]() jest
jest ![]() :
:
skąd:
czyli estymatorem największej wiarygodności dla macierzy kowariancji rozkładu normalnego jest obciążony estymator próbkowy macierzy kowariancji.
7.3. Klasyfikacja w modelu normalnym
Zrobimy dwa założenia dotyczące rozważanego wcześniej klasyfikatora:
-
Funkcja straty jest postaci:
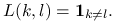
-
W każdej z grup dane pochodzą z rozkładu normalnego, czyli
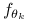 to gęstość rozkładu normalnego,
to gęstość rozkładu normalnego, 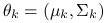 .
.
Dal zadanej funkcji straty optymalna (bayesowska) reguła decyzyjna będzie miała postać:
![d_{B}(X)=\text{argmin}_{l}\left[\sum _{{k=1}}^{K}L(k,l)\pi _{k}f(X|k)\right]=\text{argmin}_{l}\left[\sum _{{k=1}}^{K}\textbf{1}_{{k\neq l}}\pi _{k}f(X|k)\right]=](wyklady/st2/mi/mi540.png) |
![=\text{argmin}_{l}\left[\underbrace{\sum _{{k=1}}^{K}\pi _{k}f(X|k)}_{{\text{nie zależy od wyboru }l}}-\pi _{l}f(X|l)\right]=\text{argmax}_{l}\left[\pi _{l}f(X|l)\right].](wyklady/st2/mi/mi577.png) |
Znamy już postać szukanego klasyfikatora, potrzebujemy jeszcze estymatorów dla występujących w nim parametrów. Wiemy jak wyglądają estymatory ![]() :
:
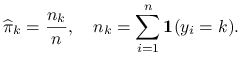 |
Estymatory największej wiarygodności dla parametrów ![]() przy założeniu normalności rozkładów w grupach są postaci:
przy założeniu normalności rozkładów w grupach są postaci:
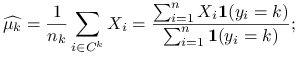 |
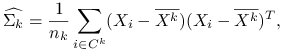 |
gdzie ![]() oznacza wektor średnich obserwacji dla
oznacza wektor średnich obserwacji dla ![]() .
.
Dla ![]() niezależnego od próby uczącej:
niezależnego od próby uczącej: ![]() estymator reguły decyzyjnej ma postać:
estymator reguły decyzyjnej ma postać:
7.3.1. Kwadratowa (qda) i liniowa (lda) funkcja klasyfikacyjna
W zależności od założeń dotyczących parametrów, możemy otrzymać klasyfikator będący różną funkcją swojego argumentu ![]() : albo kwadratową albo liniową.
: albo kwadratową albo liniową.
Kwadratowa funkcja klasyfikacyjna (qda) nie wymaga dodatkowych założeń o parametrach:
![=\text{argmax}_{l}\left[\frac{\pi _{l}}{(2\pi)^{{\frac{p}{2}}}|\Sigma _{l}|^{{\frac{1}{2}}}}\exp\left\{-\frac{1}{2}(X-\mu _{l})^{T}\Sigma _{l}^{{-1}}(X-\mu _{l})\right\}\right]=](wyklady/st2/mi/mi652.png) |
po opuszczeniu wyrażeń niezależnych od ![]() i zlogarytmowaniu:
i zlogarytmowaniu:
czyli kwadratowa funkcja argumentu ![]() .
.
Liniowa funkcja klasyfikacyjna (lda) wymaga założenia:
Dzięki niemu mamy podwójny zysk obliczeniowy: o ![]() parametrów mniej do wyestymowania i liniową funkcję optymalizowaną:
parametrów mniej do wyestymowania i liniową funkcję optymalizowaną:
ponieważ ![]() oraz
oraz ![]() nie zależy od
nie zależy od ![]() ,
,
7.4. Metody porównywania klasyfikatorów
Chcemy znaleźć taką metodę porónywania, żeby każdą obserwację spośród ![]() wykorzystać do uczenia i testu, ale tak żeby testować tylko na tych obserwacjach, które nie były brane pod uwagę przy uczeniu klasyfikatorów.
wykorzystać do uczenia i testu, ale tak żeby testować tylko na tych obserwacjach, które nie były brane pod uwagę przy uczeniu klasyfikatorów.
Kroswalidacja ![]() -krotna (walidacja krzyżowa) polega na podziale danych na
-krotna (walidacja krzyżowa) polega na podziale danych na ![]() części (popularnymi wyborami są
części (popularnymi wyborami są ![]() ,
, ![]() ):
): ![]() będzie tworzyć próbę uczącą, ostatnia będzie próbą testową. Estymujemy klasyfikatory na próbie uczącej, porównujemy metody na próbie testowej. Powtarzamy procedurę
będzie tworzyć próbę uczącą, ostatnia będzie próbą testową. Estymujemy klasyfikatory na próbie uczącej, porównujemy metody na próbie testowej. Powtarzamy procedurę ![]() razy tak, żeby każda z części była próbą testową. Dokładniej:
razy tak, żeby każda z części była próbą testową. Dokładniej:
-
Permutujemy obserwacje. Jeżeli dane mają jakąś strukturę, na przykład można je podzielić na klasy, permutujemy obserwacje w klasach.
-
Dzielimy próbę na
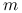 części tak, żeby w każdej z grup było po tyle samo obserwacji z każdej klasy.
części tak, żeby w każdej z grup było po tyle samo obserwacji z każdej klasy. -
Uczymy klasyfikatory na próbie uczącej - estymujemy parametry.
-
Porównujemy metody na próbie testowej (np. poprzez estymację prawdopodobieństwa poprawnej predykcji)
Definicja 7.6
Prawdopodobieństwo poprawnej predykcji to dla danego klasyfikatora ![]() . Np. jeżeli funkcja straty wyraża się wzorem
. Np. jeżeli funkcja straty wyraża się wzorem ![]() , możemy estymować prawdopodobieństwo poprawnej predykcji dla konkretnej próby treningowej i testowej następująco:
, możemy estymować prawdopodobieństwo poprawnej predykcji dla konkretnej próby treningowej i testowej następująco:
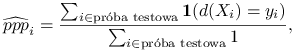 |
gdzie ![]() jest klasyfikatorem wyestymowanym na podstawie próby uczącej. Uśrednione
jest klasyfikatorem wyestymowanym na podstawie próby uczącej. Uśrednione ![]() jest dobrą metodą porównywania klasyfikatorów:
jest dobrą metodą porównywania klasyfikatorów:
7.5. Przykłady w programie R
Klasyfikacja:
-
kwadratowa funkcja klasyfikacyjna dla danych Iris, kroswalidacja: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/qda.R
-
liniowa funkcja klasyfikacyjna: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/lda.R
-
kwadratowa funkcja klasyfikacyjna oraz sieci neuronowe: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/CrossValKlasCrabs.R
-
kwadratowa funkcja klasyfikacyjna oraz sieci neuronowe, kroswalidacja: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/crossValKlas.R
-
porównanie różnych funkcji klasyfikacyjnych: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/zmDyskrym.R




