Zagadnienia
- 8.1 Predykcja cechy ciągłej
- 8.2 Metoda najmniejszych kwadratów (mnk)
- 8.3 Inne wyprowadzenie estymatora najmniejszych kwadratów
- 8.4 Estymatory metody największej wiarygodności prametrów modelu liniowego
- 8.5 Kolejne własności estymatorów mnk
- 8.6 Model liniowy przy założeniu normalności
- 8.7 Test ilorazu wiarygodności (Likelihood Ratio Test) hipotez liniowych
- 8.8 Popularne kryteria wyboru modelu – kryteria informacyjne
- 8.9 Model logistyczny – przykład uogólnionego modelu liniowego
- 8.10 Przykłady w programie R
8. Modele liniowe
8.1. Predykcja cechy ciągłej
Będziemy obserwować ciągłą zmienną objaśnianą ![]() oraz zmienne objaśniające
oraz zmienne objaśniające ![]() ,
, ![]() . Na ich podstawie będziemy chcieli znaleźć funkcję zależącą od
. Na ich podstawie będziemy chcieli znaleźć funkcję zależącą od ![]() , która będzie najlepiej przybliżać cechę
, która będzie najlepiej przybliżać cechę ![]() . Ograniczymy się przy tym tylko do zależności liniowej. Na podstawie znalezionej funkcji, dla nowo zaobserwoawanych
. Ograniczymy się przy tym tylko do zależności liniowej. Na podstawie znalezionej funkcji, dla nowo zaobserwoawanych ![]() będziemy mogli znależć predykcję
będziemy mogli znależć predykcję ![]() . Jeżeli rozpatrzymy jednowymiarowy
. Jeżeli rozpatrzymy jednowymiarowy ![]() (
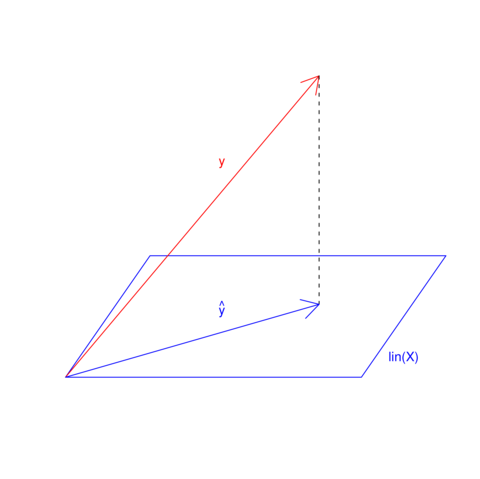
(![]() ), szukanie funkcji liniowej najlepiej przybliżającej dane obrazuje rysunek 8.1.
), szukanie funkcji liniowej najlepiej przybliżającej dane obrazuje rysunek 8.1.
Dane są postaci:
![\underbrace{\left(\begin{array}[]{c}y_{1}\\
\ldots\\
y_{n}\\
\end{array}\right)}_{{\text{losowe,obserwowane}}}=\underbrace{\left(\begin{array}[]{ccc}x_{{11}}&\ldots&x_{{1p}}\\
\ldots&\ldots&\ldots\\
x_{{n1}}&\ldots&x_{{np}}\\
\end{array}\right)}_{{\text{deterministyczne,obserwowane}}}\cdot\underbrace{\left(\begin{array}[]{c}\beta _{1}\\
\ldots\\
\beta _{p}\\
\end{array}\right)}_{{\text{szukane}}}+\underbrace{\left(\begin{array}[]{c}\varepsilon _{1}\\
\ldots\\
\varepsilon _{n}\\
\end{array}\right)}_{{\text{losowe,nieobserwowane}}}.](wyklady/st2/mi/mi851.png) |
W zapisie macierzowym:
gdzie:
-
wektor
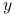 będziemy nazywać zmienną objaśnianą;
będziemy nazywać zmienną objaśnianą; -
macierz
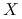 macierzą planu;
macierzą planu; -
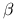 estymowanymi parametrami;
estymowanymi parametrami; -
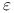 to wektor efektów losowych (wektor realizacji zmiennej losowej).
to wektor efektów losowych (wektor realizacji zmiennej losowej).
Dla tak sformułowanego problemu przyjmiemy następujące założenia:
-
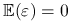 ;
; -
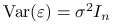 ;
; -
rząd macierzy
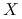 jest pełny:
jest pełny: 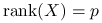 .
.
Dla tak sformułowanych danych, problem szukania estymatora parametru ![]() będziemy nazywać problemem liniowym.
będziemy nazywać problemem liniowym.
Twierdzenie 8.1
Rozkład QR macierzy
Szeroki rozkład QR: Każdą rzeczywistą macierz ![]() wymiaru
wymiaru ![]()
![]() można zapisać jako iloczyn maierzy ortogonalnej
można zapisać jako iloczyn maierzy ortogonalnej ![]() wymiaru
wymiaru ![]()
![]() oraz górnotrójkątnej macierzy
oraz górnotrójkątnej macierzy ![]() wymiaru
wymiaru ![]() :
:
![A=QR=\left(\begin{array}[]{ccc}&&\\
&Q&\\
&&\\
\end{array}\right)\left(\begin{array}[]{cc}\circ&\circ\\
&\circ\\
&\\
\end{array}\right).](wyklady/st2/mi/mi686.png) |
Wąski rozkład QR: Ponieważ ![]() dolnych wierzy macierzy
dolnych wierzy macierzy ![]() jest zerowa, można skrócić zapis do
jest zerowa, można skrócić zapis do
![=\left(\begin{array}[]{cc}&\\
&Q_{1}\\
&\\
\end{array}\right)\left(\begin{array}[]{cc}\circ&\circ\\
&\circ\\
\end{array}\right).](wyklady/st2/mi/mi891.png) |
gdzie ![]() jest macierzą wymairu
jest macierzą wymairu ![]() o ortogonalnych kolumnach a
o ortogonalnych kolumnach a ![]() jest macierzą górnotrójkątną wymairu
jest macierzą górnotrójkątną wymairu ![]() .
.
Wąski rozkład QR jest zapisem macierzowym ortogonalizacji Gramma-Schmidta układu wektorów będących kolumnami macierzy ![]() . Szeroki rozkład otrzymujemy dopełniając macierz
. Szeroki rozkład otrzymujemy dopełniając macierz ![]() do bazy przestrzeni
do bazy przestrzeni ![]() .
.
Problem 8.1
Przy założeniu modelu liniowego, będziemy chcieli wyestymować nieznane parametry: ![]() i
i ![]() .
.
8.2. Metoda najmniejszych kwadratów (mnk)
Zauważmy, że
Estymator najmnieszych kwadratów parametru ![]() to taka jego wartość, dla której odległości euklidesowe przybliżanych danych od prostej je przybliżających jest najmniejsza:
to taka jego wartość, dla której odległości euklidesowe przybliżanych danych od prostej je przybliżających jest najmniejsza:
Twierdzenie 8.2
Estymator najmniejszych kwadratów wyraża się wzorem
gdzie ![]() i
i ![]() pochodzą z wąskiego rozkładu QR macierzy planu
pochodzą z wąskiego rozkładu QR macierzy planu ![]() .
.
Skorzystajmy z szerokiego rozkładu QR macierzy ![]() :
: ![]() . Ponieważ mnożenie wektora przez macierz ortogonalną nie zmienia jego normy, możemy zapisać:
. Ponieważ mnożenie wektora przez macierz ortogonalną nie zmienia jego normy, możemy zapisać:
Wyrażenie to osiąga minimum ze względu na parametr ![]() , jeżeli wyzerujemy pierwszy składnik sumy:
, jeżeli wyzerujemy pierwszy składnik sumy:
Ponieważ macierz ![]() jest kwadratowa i pełnego rzędu (rank
jest kwadratowa i pełnego rzędu (rank![]() ), możemy ją odwrócić:
), możemy ją odwrócić:
Wniosek 8.1
Zauważmy, że:
-
Predykcja dla
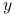 jest równa
jest równa 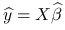 ;
; -
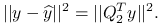
(8.1)
Przyjrzyjmy się własnościom metody najmniejszych kwadratów (zostaną one udowodnione w dalszej części wykładu):
-
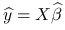 jest rzutem ortogonalnym
jest rzutem ortogonalnym 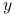 na przestrzeń rozpiętą przez kolumny macierzy planu
na przestrzeń rozpiętą przez kolumny macierzy planu 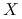 .
. -
Nieobciążonym estymatorem parametru
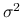 jest
jest 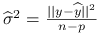 .
. -
Twierdzenie Gaussa-Markowa: estymator
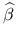 jest liniowym, nieobciążonym estymatorem o najmniejszej wariancji parametru
jest liniowym, nieobciążonym estymatorem o najmniejszej wariancji parametru 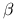 (BLUE- Best Linear Unbiased Estimator).
(BLUE- Best Linear Unbiased Estimator). -
Przy założeniu
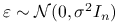 , zachodzi twierdzenie Fishera:
, zachodzi twierdzenie Fishera:-
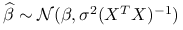 ;
; -
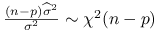 ;
; -
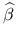 i
i 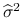 są niezależne.
są niezależne.
-
8.3. Inne wyprowadzenie estymatora najmniejszych kwadratów
Wyprowadzimy estymator mnk jako rozwiązanie zadania BLUE – liniowy, nieobciążony estymator o najmniejszej wariancji. Rozumowanie będzie jednocześnie dowodem twierdzenia Gaussa-Markowa.
Twierdzenie 8.3
Dla problemu liniowego estymator postaci ![]() jest liniowym, nieobciążonym estymatorem o najmniejszej wariancji parametru
jest liniowym, nieobciążonym estymatorem o najmniejszej wariancji parametru ![]() .
.
Żeby łatwiej mówić o nieobciążoności, czy minimalnej wariancji, zredukujemy wymiar problemu do jednowymiarowego zakładając, że własności będą zachodzić dla wszystkich możliwych kombinacji liniowych zmiennej objaśnianej:
Dla danego wektora ![]() , konstruujemy kombinację liniową
, konstruujemy kombinację liniową ![]() i szukamy dla niej estymatora zależącego liniowo od
i szukamy dla niej estymatora zależącego liniowo od ![]() :
:
przy założeniu nieobciążoności:
Jednocześnie wiemy, że:
Stąd:
Będziemy minimalizować wariancję estymatora ![]() :
:
Zadanie optymalizacyjne wygląda następująco:
Skorzystajmy z metody mnożników Lagrange'a:
![\min _{c}\left[F(c,\lambda)=\sigma^{2}c^{T}c+(c^{T}X-l^{T})\underbrace{\lambda}_{{\text{wektor}}}\right].](wyklady/st2/mi/mi897.png) |
Szukamy estymatora wektora ![]() , spełniającego dwa równania:
, spełniającego dwa równania:
| (8.2) |
| (8.3) |
Z równania 8.2 otrzymujemy: ![]() , wstawiamy do równania 8.3:
, wstawiamy do równania 8.3:
skąd:
Macierz ![]() jest pełnego rzędu, więc macierz
jest pełnego rzędu, więc macierz ![]() jest odwracalna. Wstawiając
jest odwracalna. Wstawiając ![]() do wzoru na
do wzoru na ![]() , otrzymujemy:
, otrzymujemy:
Estymator ![]() jest więc postaci:
jest więc postaci:
podstawiając za ![]() kolejne wektory bazy kanonicznej
kolejne wektory bazy kanonicznej ![]() , znajdujemy kolejne estymatory kombinacji liniowych
, znajdujemy kolejne estymatory kombinacji liniowych ![]() , co łącznie możemy zapisać jako:
, co łącznie możemy zapisać jako:
Stwierdzenie 8.1
Liniowy, nieobciążony estymator o najmniejszej wariancji parametru ![]() w modelu liniowym jest równy estymatorowi najmniejszych kwadratów.
w modelu liniowym jest równy estymatorowi najmniejszych kwadratów.
korzystając z wąskiego rozkładu QR: ![]() ,
,
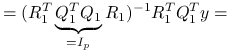 |
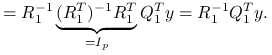 |
8.4. Estymatory metody największej wiarygodności prametrów modelu liniowego
Estymatory największej wiarygodności to takie wartości parametrów, których prawdopodobieństwo zaobserwowania danych jest największe. Żeby skorzystać z tej metody estymacji, potrzebna jest funkcja wiarygodności, niezbędne więc będzie założenie na temat rozkładu danych:
Zamiast zakładać:
założymy:
skąd mamy ![]() oraz funkcję wiarygodności:
oraz funkcję wiarygodności:
![f_{{\beta,\sigma^{2}}}(y_{1},\ldots,y_{n})=f_{{\beta,\sigma^{2}}}(y)=\frac{1}{(2\pi)^{{\frac{n}{2}}}|\sigma^{2}I_{n}|^{{\frac{1}{2}}}}\exp\left[-\frac{1}{2}(y-X\beta)\sigma^{{-2}}I_{n}(y-X\beta)\right]=](wyklady/st2/mi/mi707.png) |
Funkcję wiarygodności będziemy chcieli zmaksymalizować po parametrach ![]() i
i ![]() . Ponieważ logarytm jest funkcją rosnącą, jest to równoważne z maksymalizacją logarytmu funkcji wiarygodności:
. Ponieważ logarytm jest funkcją rosnącą, jest to równoważne z maksymalizacją logarytmu funkcji wiarygodności:
gdzie ![]() jest stałą niezależną od szukanych parametrów. Zadanie maksymalizacji logwiarygodności
jest stałą niezależną od szukanych parametrów. Zadanie maksymalizacji logwiarygodności ![]() jest rónoważne minimalizacji
jest rónoważne minimalizacji ![]() :
:
Część sumy zależąca od parametru ![]() to
to ![]() . Wartością parametru
. Wartością parametru ![]() minimalizującą to wyrażenie jest:
minimalizującą to wyrażenie jest:
co udowodniliśmy już w twierdzeniu 8.2.
Ponieważ ![]() nie zależy od parametru
nie zależy od parametru ![]() , mogę wstawić estymator do funkcji wiarygodności przy szukaniu optymalnego parametru
, mogę wstawić estymator do funkcji wiarygodności przy szukaniu optymalnego parametru ![]() . Oznaczmy także
. Oznaczmy także ![]() żeby nie mylił się nam kwadrat przy parametrze:
żeby nie mylił się nam kwadrat przy parametrze:
skąd otrymujemy:
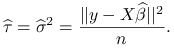 |
Wniosek 8.2
Przy założeniu rozkładu normalnego:
-
estymatory parametru
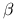 dla metody największej wiarygodności i metody najmniejszych kwadratów są równe:
dla metody największej wiarygodności i metody najmniejszych kwadratów są równe: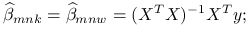
-
estymatory parametru
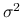 dla metody największej wiarygodności i metody najmniejszych kwadratów są równe z dokładnością do stałej:
dla metody największej wiarygodności i metody najmniejszych kwadratów są równe z dokładnością do stałej: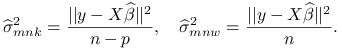
8.5. Kolejne własności estymatorów mnk
8.5.1. Wartość oczekiwana i wariancja estymatora 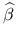
-
Wartość oczekiwana:
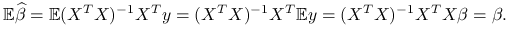
(8.4) Estymator jest niebciążony.
-
Macierz wariancji:
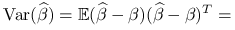
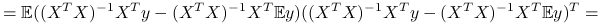
^{{-1}}X^{T})^{T}=](wyklady/st2/mi/mi837.png)
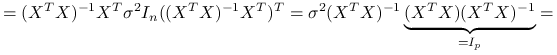
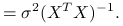
(8.5)
8.5.2. Dopasowanie 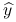 jako rzut ortogoanlny
jako rzut ortogoanlny 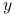 na przestrzeń rozpiętą przez kolumny macierzy
na przestrzeń rozpiętą przez kolumny macierzy 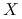
Prypomnijmy
Definicja 8.1
Macierzą daszkową ![]() nazwiemy taką macierz, że:
nazwiemy taką macierz, że:
Stąd:
Stwierdzenie 8.2
Zauważmy, że ![]() jest nieobciążonym estymatorem
jest nieobciążonym estymatorem ![]() :
:
Stwierdzenie 8.3
Własności macierzy daszkowej ![]() :
:
-
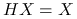 :
: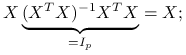
-
macierz
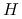 jest idempotentna, czyli
jest idempotentna, czyli 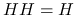 :
: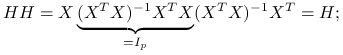
-
symetryczna, czyli
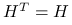 :
: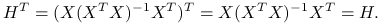
-
korzystając z wąskiego rozkładu QR macierzy
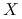 ,
, 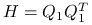 :
: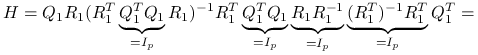
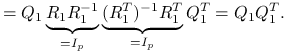
-
korzystając z szerokiego rozkładu QR macierzy
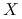 , możemy przyjrzeć się rozkładowi spektralnemu macierzy daszkowej:
, możemy przyjrzeć się rozkładowi spektralnemu macierzy daszkowej: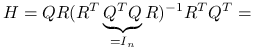
ponieważ
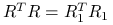 ,
,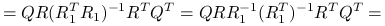
![=\underbrace{Q\left(\begin{array}[]{cccc}1&&&\\
&\ldots&&\\
&&1&\\
&&&0\\
\end{array}\right)Q^{T}}_{{\text{rozkład spektralny macierzy }H}}=](wyklady/st2/mi/mi757.png)
dla
![Q=[q_{1},\ldots,q_{p},\ldots,q_{n}]](wyklady/st2/mi/mi943.png) :
: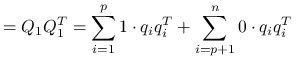
Wniosek 8.3
-
Macierz daszkowa
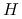 jest macierzą rzutu ortogonalnego na przestrzeń rozpiętą przez kolumny macierzy
jest macierzą rzutu ortogonalnego na przestrzeń rozpiętą przez kolumny macierzy 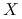 .
. -
Jeżeli
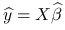 minimalizuje wyrażenie
minimalizuje wyrażenie 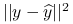 , to jest rzutem ortogonalnym
, to jest rzutem ortogonalnym 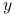 na
na 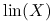 .
.
8.5.3. Nieobciążony estymator parametru 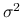
Stwierdzenie 8.4
Macierz ![]() jest macierzą rzutu ortogonalnego na przestrzeń prostopadłą do przestrzeni rozpiętej przez kolumny macierzy
jest macierzą rzutu ortogonalnego na przestrzeń prostopadłą do przestrzeni rozpiętej przez kolumny macierzy ![]() , jest więc w szczególności symetryczna i idempotentna.
, jest więc w szczególności symetryczna i idempotentna.
Wniosek 8.4
Ponieważ ślad macierzy równy jest sumie jego wartości własnych, ślady macierzy daszkowej ![]() i macierzy
i macierzy ![]() to:
to:
Stwierdzenie 8.5
Twierdzenie Pitgorasa w postaci macierzowej:
ponieważ macierze ![]() i
i ![]() są symetryczne i idempotentne, zachodzi:
są symetryczne i idempotentne, zachodzi:
| (8.6) |
Stwierdzenie 8.6
Niebciążonym estymatorem parametru ![]() w modelu liniowym jest:
w modelu liniowym jest:
Ponieważ ![]() jest nieobciążonym estymatorem
jest nieobciążonym estymatorem ![]() , możemy zapisać:
, możemy zapisać:
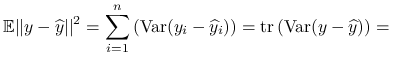 |
Stąd:
8.5.4. Model z większą liczbą parametrów nie musi być lepiej dopasowany dla nowych danych
-
Błąd predykcji
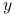 za pomocą
za pomocą 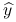 na tej samej próbie, korzystając ze wzoru 8.6, można zapisać w postaci:
na tej samej próbie, korzystając ze wzoru 8.6, można zapisać w postaci: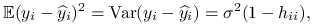
gdzie
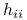 jest elementem macierzy daszkowej:
jest elementem macierzy daszkowej: 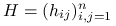 .
.Definicja 8.2
Elementy przekątnej macierzy daszkowej
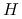 :
: 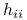 będziemy nazywać ładunkami obserwsacji
będziemy nazywać ładunkami obserwsacji 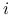 -tej i oznaczać
-tej i oznaczać 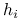 .
. -
Dla nowych obserwacji mamy:
Zakładamy niezależność nowych obserwacji zmiennej objaśnianej i
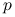 -wymiarowego wektora zmiennych objaśniających:
-wymiarowego wektora zmiennych objaśniających: 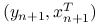 od
od 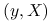 . Będziemy estymować parametry używając danych treningowych
. Będziemy estymować parametry używając danych treningowych 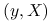 , a obliczać błąd dla nowych danych testowych:
, a obliczać błąd dla nowych danych testowych: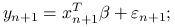
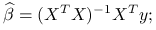
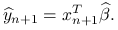
Błąd predykcji jest równy:
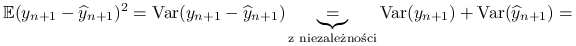
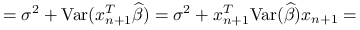
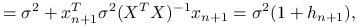
gdzie
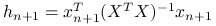 , analogicznie do ładunków obserwacji dla
, analogicznie do ładunków obserwacji dla 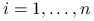 :
: 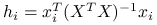 .
. -
Porównanie obu błędów predykcji dla tej samej macierzy planu:
Dane treningowe, dla których będziemy estymować parametr
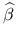 to
to 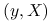 gdzie
gdzie 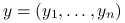 . Dane testowe, dla których będziemy liczyć błąd predykcji to w pierwszym przypadku ten sam zbiór
. Dane testowe, dla których będziemy liczyć błąd predykcji to w pierwszym przypadku ten sam zbiór 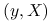 , a w drugim
, a w drugim 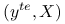 gdzie
gdzie 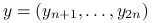 są nowymi obserwacjami, a macierz planu
są nowymi obserwacjami, a macierz planu 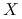 pozostaje niezmieniona. Porównajmy uśrednione oba błędy predykcji:
pozostaje niezmieniona. Porównajmy uśrednione oba błędy predykcji: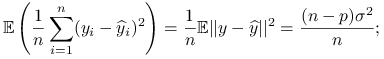
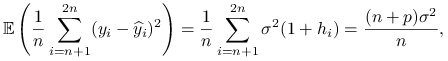
gdzie korzystamy z równości
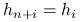 , co zachodzi dzięki użyciu tej samej macierzy planu
, co zachodzi dzięki użyciu tej samej macierzy planu 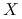 w zbiorze treningowym i testowym oraz własnści macierzy daszkowej
w zbiorze treningowym i testowym oraz własnści macierzy daszkowej 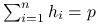 .
.Wniosek 8.5
Na podstawie obliczonych błędów predykcji możemy wywnioskować:
-
Większy model nie zawsze oznacza lepsze dopasowanie.
-
Różnica pomiędzy błędami predykcji wynosi:
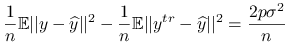
-
8.5.5. Kroswalidacja leave-one-out
Estymację błędu predykcji można oprzeć na kroswalidacji leave-one-out. Dla każdej obserwacji będziemy estymować model za pomocą wszystkich obserwacji oprócz niej samej i obliczać błąd predykcji na nowych danych dla tej pominiętej obserwacji. W ten sposób dostaniemy ![]() błędów predykcji, które następnie uśrednimy.
błędów predykcji, które następnie uśrednimy.
Niech ![]() ,
, ![]() oznacza macierz
oznacza macierz ![]() z usuniętą
z usuniętą ![]() -tą obserwacją (
-tą obserwacją (![]() -tym wierszem),
-tym wierszem), ![]() wektor obserwacji z usuniętą
wektor obserwacji z usuniętą ![]() -tą obserwacją. Estymator
-tą obserwacją. Estymator ![]() będzie oznaczać estymator mnk na podstawie danych
będzie oznaczać estymator mnk na podstawie danych ![]() :
:
Predykcja dla pominiętej obserwacji wyraża się wzorem:
gdzie tak jak przy liczeniu błędu predykcji na nowych danych, ![]() jest niezależne od
jest niezależne od ![]() .
.
Korzystając z tego, że ![]() , otrzymujemy:
, otrzymujemy:
gdzie ![]() to
to ![]() -ty wyraz na przekątnej macierzy daszkowej dla pełnej macierzy
-ty wyraz na przekątnej macierzy daszkowej dla pełnej macierzy ![]() :
: ![]() . Fakt ostatniej równości w powyższym wzorze przyjmiemy bez dowodu.
. Fakt ostatniej równości w powyższym wzorze przyjmiemy bez dowodu.
Wniosek 8.6
Estymator błędu predykcji przy użyciu kroswalidacji leave-one-out można uprościć do wzoru:
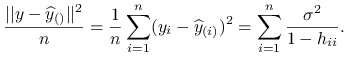 |
(8.7) |
8.6. Model liniowy przy założeniu normalności
Zamiast w modelu liniowym zakładać:
założymy:
Dzięki takiemu sformułowaniu zadania, będziemy mogli znaleźć rozkłady estymatorów ![]() i
i ![]() , co umożliwi wnioskowanie statystyczne na ich temat, na przykład kondtrukcję przedziałów ufności. Udowodnimy:
, co umożliwi wnioskowanie statystyczne na ich temat, na przykład kondtrukcję przedziałów ufności. Udowodnimy:
Twierdzenie 8.4 (Fishera)
Przy założeniu ![]() , estymatory modelu liniowego spełniają:
, estymatory modelu liniowego spełniają:
-
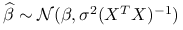 ;
; -
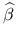 i
i 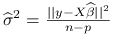 są niezależne;
są niezależne; -
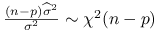 ;
;
Ponieważ ![]() , mamy:
, mamy:
| (8.8) |
Wiemy, że nieobciążonymi estymatorami parametrów modelu liniowego są:
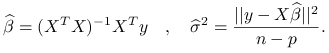 |
-
Rozkład
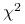 z
z  stopniami swobody to suma
stopniami swobody to suma  kwadratów niezależnych zmiennych losowych o rozkładzie standardowym normalnym. Udowodnimy, że
kwadratów niezależnych zmiennych losowych o rozkładzie standardowym normalnym. Udowodnimy, że 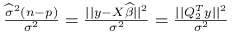 ma rozkład
ma rozkład 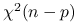 .
.Z rozkładu QR macierzy
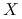 znamy wymiary macierzy
znamy wymiary macierzy 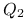 , długość wektora
, długość wektora 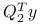 to
to  . Oznaczmy:
. Oznaczmy: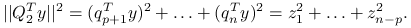
Udowodnimy, że
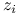 ,
,  są niezależne i mają rozkład
są niezależne i mają rozkład 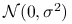 .
.Współrzędne wektora
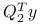 są niezależnymi zmiennymi losowymi o rozkładzie normalnym. Normalność wynika z twierdzenia 8.2, niezależność z braku korelacji (8.9). Ze wzoru 8.9 widzimy także, że wariancje
są niezależnymi zmiennymi losowymi o rozkładzie normalnym. Normalność wynika z twierdzenia 8.2, niezależność z braku korelacji (8.9). Ze wzoru 8.9 widzimy także, że wariancje 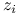 są równe
są równe 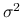 .
.Współrzędne wektora
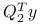 mają wartość oczekiwaną równą zero:
mają wartość oczekiwaną równą zero: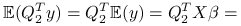
z wąskiego rozkładu QR macierzy
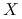 ,
,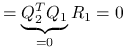
z ortogonalności kolumn macierzy
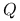 .
.Otrzymujemy więc:
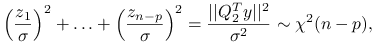
gdzie
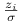 są niezależnymi zmiennymi losowymi o rozkładzie
są niezależnymi zmiennymi losowymi o rozkładzie 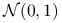 .
.
8.7. Test ilorazu wiarygodności (Likelihood Ratio Test) hipotez liniowych
Hipotezy liniowe przy założeniach modelu liniowego można ogólnie sformułować jako:
gdzie macierz ![]() jest wymiaru
jest wymiaru ![]() , a macierz
, a macierz ![]() wymiaru
wymiaru ![]() .
.
Przykład 8.1
Jeżeli wektor współczynników jest postaci:
![\beta=\left(\begin{array}[]{c}\beta _{1}\\
\beta _{2}\\
\beta _{3}\\
\beta _{4}\\
\end{array}\right)](wyklady/st2/mi/mi936.png) |
i chcemy nałożyć ograniczenie liniowe na parametry: ![]() , to można go zapisać postaci:
, to można go zapisać postaci:
![\underbrace{\left(\begin{array}[]{cccc}0&1&-1&0\\
\end{array}\right)}_{{A}}\beta=0.](wyklady/st2/mi/mi815.png) |
8.7.1. LRT ogólnie
Ogólnie test ilorazu wiarygodności dotyczący parametru ![]() rozkładu zmiennej losowej
rozkładu zmiennej losowej ![]() można zapisać jako:
można zapisać jako:
gdzie ![]() oznacza gęstość rozkładu zmiennej
oznacza gęstość rozkładu zmiennej ![]() zależącą od parametru
zależącą od parametru ![]() .
.
Statystyka testowa wyraża się wzorem:
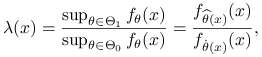 |
gdzie:
Uwaga 8.1
Jeżeli ![]() to:
to:
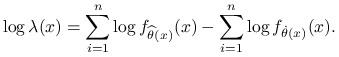 |
8.7.2. Modele zagnieżdżone
Z modelem zagnieżdżonym mamy do czynienia gdy ![]() .
.
Rozpatrzmy następujący problem:
Dla hipotez liniowych mamy:
wtedy typowo ![]() , skąd możemy zapisać:
, skąd możemy zapisać:
Dzięki takiemu zapisowi upraszcza się wzór na statystykę testową LRT:
Twierdzenie 8.5 (Asymptotyczny rozkład LRT)
Przy założeniach: ![]() otwarty,
otwarty, ![]() regularna rodzina gęstości,
regularna rodzina gęstości, ![]() funkcja gładka,
funkcja gładka, ![]() :
:
gdzie ![]() oznacza dystrybuantę rozkładu
oznacza dystrybuantę rozkładu ![]() o
o ![]() stopniach swobody.
stopniach swobody.
8.7.3. LRT w modelu liniowym
Wracamy teraz do modelu linowego i zakładamy normalność rozkładu ![]() :
:
gdzie ![]() ma wymiary
ma wymiary ![]() ,
, ![]() wymiary
wymiary ![]() ;
;
Dla tak sformułowanego zadania wiemy, że rozkład danych ![]() jest normalny i wyraża się wzorem:
jest normalny i wyraża się wzorem:
gdzie ![]() .
.
Stwierdzenie 8.7
Statystyka testowa testu ilorazu wiarygodności dla ![]() jest równa:
jest równa:
![\lambda(y)=\left[\frac{\dot{\sigma}^{2}}{\widehat{\sigma}^{2}}\right]^{{\frac{n}{2}}}=\left[\frac{||y-X\dot{\beta}||^{2}}{||y-X\widehat{\beta}||^{2}}\right]^{{\frac{n}{2}}},](wyklady/st2/mi/mi881.png) |
(8.10) |
gdzie:
![\lambda(y)=\frac{f_{{\widehat{\theta}(y)}}(y)}{f_{{\dot{\theta}(y)}}(y)}=\frac{\frac{1}{(\sqrt{2\pi})^{n}}\frac{1}{(\widehat{\sigma}^{2})^{{\frac{n}{2}}}}\exp\left[-\frac{1}{2}\frac{||y-X\widehat{\beta}||^{2}}{\widehat{\sigma}^{2}}\right]}{\frac{1}{(\sqrt{2\pi})^{n}}\frac{1}{(\dot{\sigma}^{2})^{{\frac{n}{2}}}}\exp\left[-\frac{1}{2}\frac{||y-X\dot{\beta}||^{2}}{\dot{\sigma}^{2}}\right]}=\clubsuit](wyklady/st2/mi/mi930.png) |
korzystając z postać estymatora największej wiarygodności dla parametru ![]() w modelu liniowym, możemy zapisać:
w modelu liniowym, możemy zapisać:
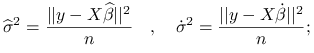 |
pdstawiając otrzymujemy:
![\clubsuit=\frac{\frac{1}{(\widehat{\sigma}^{2})^{{\frac{n}{2}}}}\exp\left[-\frac{1}{2}\frac{\widehat{\sigma}^{2}}{n\widehat{\sigma}^{2}}\right]}{\frac{1}{(\dot{\sigma}^{2})^{{\frac{n}{2}}}}\exp\left[-\frac{1}{2}\frac{\dot{\sigma}^{2}}{n\dot{\sigma}^{2}}\right]}=\left[\frac{\dot{\sigma}^{2}}{\widehat{\sigma}^{2}}\right]^{{\frac{n}{2}}}.](wyklady/st2/mi/mi933.png) |
Stwierdzenie 8.8
Statystyka testowa
![\lambda(y)=\left[\frac{\dot{\sigma}^{2}}{\widehat{\sigma}^{2}}\right]^{{\frac{n}{2}}}](wyklady/st2/mi/mi818.png) |
jest równoważna statystyce:
gdzie ![]() ,
, ![]() .
.
Ze wzoru 8.10 widzimy, że:
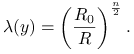 |
Statystyka ![]() jako iloraz norm dwóch wektorów, jest nieujemna, a dla
jako iloraz norm dwóch wektorów, jest nieujemna, a dla ![]() dodatnia z dodatniości
dodatnia z dodatniości ![]() i
i ![]() .
Istnieje rosnące przekształcenie
.
Istnieje rosnące przekształcenie ![]() w
w ![]() dla
dla ![]() , więc statystyki są rónoważne.
, więc statystyki są rónoważne.
Twierdzenie 8.6
Statystyka ![]() przy
przy ![]() ma rozkład
ma rozkład ![]() -Snedecora:
-Snedecora:
Zmieńmy oznaczenia dotyczące macierzy planu. Macierz ![]() gdzie
gdzie ![]() będą oznaczać kolumny macierzy, zwane predyktorami. Możemy wtedy zapisac:
będą oznaczać kolumny macierzy, zwane predyktorami. Możemy wtedy zapisac:
Wiemy, że:
gdzie
przestrzenie ![]() i
i ![]() są przestrzeniami liniowymi o wymiarach:
są przestrzeniami liniowymi o wymiarach:
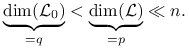 |
Ortogonalizujemy bazę przestrzeni ![]() , uzupełniamy do bazy
, uzupełniamy do bazy ![]() , a następnie do bazy
, a następnie do bazy ![]() . Oznaczmy:
. Oznaczmy:
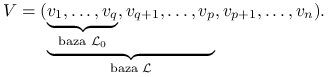 |
oraz:
Zauważmy, że wektory te są postaci:
![Z=\left(\begin{array}[]{c}z_{1}\\
\ldots\\
z_{q}\\
\ldots\\
z_{p}\\
\ldots\\
\ldots\\
z_{n}\\
\end{array}\right)\quad\widehat{Z}=\left(\begin{array}[]{c}\widehat{z}_{1}\\
\ldots\\
\widehat{z}_{q}\\
\ldots\\
\widehat{z}_{p}\\
0\\
\ldots\\
0\\
\end{array}\right)\quad\dot{Z}=\left(\begin{array}[]{c}\dot{z}_{1}\\
\ldots\\
\dot{z}_{q}\\
0\\
\ldots\\
\ldots\\
\ldots\\
0\\
\end{array}\right).](wyklady/st2/mi/mi720.png) |
Możemy wtedy zapisać:
ponieważ mnożenie wektora przez macierz ortogonalną nie zmienia jego normy,
Najlepszymi dopasowaniami ![]() do
do ![]() oraz
oraz ![]() do
do ![]() minimalizującymi błędy średniokwadratowe
minimalizującymi błędy średniokwadratowe ![]() i
i ![]() są:
są:
![\dot{Z}=\left(\begin{array}[]{c}\dot{z}_{1}=z_{1}\\
\ldots\\
\dot{z}_{q}=z_{q}\\
0\\
\ldots\\
\ldots\\
0\\
\end{array}\right)\quad\widehat{Z}=\left(\begin{array}[]{c}\widehat{z}_{1}=z_{1}\\
\ldots\\
\ldots\\
\widehat{z}_{p}=z_{p}\\
0\\
\ldots\\
0\\
\end{array}\right)](wyklady/st2/mi/mi713.png) |
Stąd:
Ponieważ założyliśmy rozkład normalny dla ![]() , możemy zapisać:
, możemy zapisać:
a także, ponieważ ![]() jest macierzą ortogonalną:
jest macierzą ortogonalną:
| (8.11) |
Współrzędne wektora ![]() :
: ![]() mają więc rozkłady normalne i są niezależne (bo nieskorelowane). Co więcej, przy założeniu hipotezy zerowej,
mają więc rozkłady normalne i są niezależne (bo nieskorelowane). Co więcej, przy założeniu hipotezy zerowej, ![]() , czyli jest postaci:
, czyli jest postaci:
![X\beta=\left(\begin{array}[]{c}w_{1}\\
\ldots\\
w_{q}\\
0\\
\ldots\\
0\\
\end{array}\right)](wyklady/st2/mi/mi738.png) |
w bazie ![]() . Ze wzoru 8.11,
. Ze wzoru 8.11, ![]() , czyli:
, czyli:
Widzimy teraz, że wyrażenie:
ma rozkład ![]() , a wyrażenie:
, a wyrażenie:
rozkład ![]() oraz oba wyrażenia są od siebie ziezależne.
Wróćmy do postaci statystyki F:
oraz oba wyrażenia są od siebie ziezależne.
Wróćmy do postaci statystyki F:
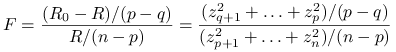 |
ma więc rozkład ![]() .
.
Uwaga 8.2
Zauważmy ciekawą własność bazującą na dowodzie twierdzenia: dla ![]()
![]() przy modelu postaci:
przy modelu postaci:
![y=\left(\begin{array}[]{cccc}1&&&\\
1&&\star&\\
\ldots&&&\\
1&&&\\
\end{array}\right)\left(\begin{array}[]{c}\beta _{0}\\
\beta _{1}\\
\ldots\\
\beta _{p}\\
\end{array}\right)+\varepsilon,](wyklady/st2/mi/mi910.png) |
możemy zapisać:
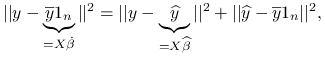 |
gdzie ![]() jest średnią arytmetyczną z obserwacji w wektorze
jest średnią arytmetyczną z obserwacji w wektorze ![]() .
.
Wniosek 8.7
Testowanie hipotez o istotności współczynników (testowanie hipotez, czy kolejne grupy ![]() są równe zeru) służy wyborowi modelu (podzbioru zmiennych objaśniających
są równe zeru) służy wyborowi modelu (podzbioru zmiennych objaśniających ![]() ).
).
8.8. Popularne kryteria wyboru modelu – kryteria informacyjne
W poprzednim rozdziale zostało opisane testowanie hipotez o istotności współczynników jako sposób wyboru modelu. Wybór predyktorów można także oprzeć na minimalizacji estymatora błędu predykcji wyliczonego na podstawie kroswalidacji leave-one-out (8.7). Opiszemy teraz jeszcze inną metodę wyboru zmiennych objaśniających bazującą na tak zwanych kryteriach informacyjnych postaci:
które obliczane są dla każdego modelu (dla każdego podzbioru ![]() predyktorów) i wybierany jest ten minimalnej wartości kryterium. Dwa popularne kryteria informacyjne:
predyktorów) i wybierany jest ten minimalnej wartości kryterium. Dwa popularne kryteria informacyjne:
-
Akaike Information Criterion (AIC):
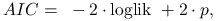
gdzie
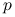 to liczba zmiennych objaśniających w modelu.
to liczba zmiennych objaśniających w modelu. -
Bayes Information Criterion (BIC):
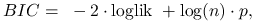
gdzie
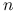 to liczba obserwacji w modelu.
to liczba obserwacji w modelu.
Przy założeniach modelu liniowego i normalności rozkładu ![]() , kryteria przyjmują łatwiejszą postać:
, kryteria przyjmują łatwiejszą postać:
-
Przy znanym
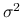 :
: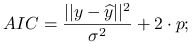
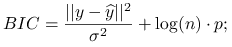
-
Przy nieznanym
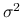 :
: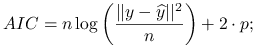
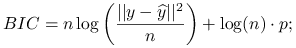
8.9. Model logistyczny – przykład uogólnionego modelu liniowego
Modelu logistycznego używa się do objaśniania zmiennej binarnej, czyli przyjmującej wartości ze zbioru ![]() . Poprzednio zakładaliśmy:
. Poprzednio zakładaliśmy:
gdzie wektor ![]() oznacza wiersz macerzy planu.
oznacza wiersz macerzy planu.
Teraz będziemy zakładać rozkład:
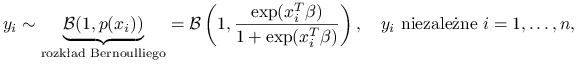 |
gdzie postać funkcji ![]() można tłumaczyć tym, że prawdopodobieństwo powinno przyjmować wartości z przedziału
można tłumaczyć tym, że prawdopodobieństwo powinno przyjmować wartości z przedziału ![]() .
Parametry modelu (
.
Parametry modelu (![]() ) estymuje się metodą największej wiarygodności, gdzie funkcja wiarygodności jest równa:
) estymuje się metodą największej wiarygodności, gdzie funkcja wiarygodności jest równa:
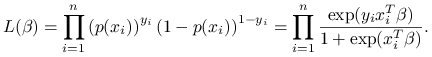 |
Logarytm funkcji wiarygodności maksymalizuje się numerycznie aby otrzymać estymatory ![]() . Predykcję w modelu można oprzeć na klasyfikatorze:
. Predykcję w modelu można oprzeć na klasyfikatorze:
gdzie ![]() jest wektorem nowych obserwacji. Przewidywany na podstawie modelu
jest wektorem nowych obserwacji. Przewidywany na podstawie modelu ![]() to wtedy:
to wtedy:
8.10. Przykłady w programie R
Model liniowy:
-
regresja liniowa z diagnostyką dla danych Bodyfat: http://www.mimuw.edu.pl/~pokar/StatystykaII/DANE/bodyfat.R
-
regresja liniowa z diagnostyką dla danych Samochody: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/samochodyNowe.R
-
regresja liniowa dla danych Iris: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/lm.R
-
regresja liniowa dla danych Samochody: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/samochody.R
-
porównanie metody najmniejszych kwadratów i sieci neuronowych: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/crossValRegr.R
Logit (model logistyczny):
-
estymacja parametrów: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/logit.R
-
estymacja parametrów i rysowanie wyników: http://www.mimuw.edu.pl/~pokar/StatystykaII/PREDYKCJA/Orings.R