Zagadnienia

10.1 Sterowalność — rozdział
10.2 Obserwowalność — rozdział
10.3 Sterowania bang-bang
10.4 Sterowalność ukladów nieliniowych — rozdział
10.5 Zasada maksimum — rozdziały ,
10.6 Przykłady

10. Zadania

Tomasz Cieślak

10.1. Sterowalność — rozdział 2

Definicja 10.1

O sterowalności regularnej mówimy, jeśli jesteśmy w stanie sterować naszym układem za pomocą każdego pojedyńczego sterowania ze zbioru możliwych sterowań.

Ćwiczenie 10.1

Pokazać, że układ sterowalny nie musi być regularnie sterowalny.

Ćwiczenie 10.2

Niech $x:[0,T]\rightarrow{\mathbb{R}}^{3}$ będzie dane przez $\left[\begin{array}[]{ll}x^{1}(t)\\ x^{2}(t)\\ x^{3}(t)\\ \end{array}\right]$ , natomiast $u:[0,T]\rightarrow{\mathbb{R}}^{2}$ przez $\left[\begin{array}[]{ll}u^{1}(t)\\ u^{2}(t)\\ \end{array}\right]$ .

Macierze $A$ oraz $B$ dane są odpowiednio przez $\left[\begin{array}[]{lll}1&0&1\\ 0&1&2\\ 1&0&0\\ \end{array}\right]$ i $\left[\begin{array}[]{ll}1&0\\ 0&1\\ 0&1\\ \end{array}\right].$

Czy układ

$\dot{x}=Ax+Bu$

(10.1)

jest sterowalny? Czy jest on regularnie sterowalny?

Ćwiczenie 10.3

Czy układ (10.1) jest regularnie sterowalny dla $x:[0,T]\rightarrow{\mathbb{R}}^{2}$ oraz $A=\left[\begin{array}[]{ll}1&2\\ 0&1\\ \end{array}\right]\,,\;$ $B=\left[\begin{array}[]{ll}2&0\\ 1&1\\ \end{array}\right]\;?$

Ćwiczenie 10.4

Niech $x:[0,T]\rightarrow{\mathbb{R}}^{2}$ oraz $u:[0,T]\rightarrow[-1,1]^{{3}}$ , czy wówczas układ (10.1), dla którego

$A=\left[\begin{array}[]{lll}1&0&0\\ 0&2&1\\ 1&0&1\\ \end{array}\right],$ $B=\left[\begin{array}[]{lll}1&0&1\\ 0&1&0\\ 1&0&0\\ \end{array}\right]\;$ jest sterowalny całkowicie oraz czy jest sterowalny lokalnie?

10.2. Obserwowalność — rozdział 3

Ćwiczenie 10.5

Niech $x:[0,T]\rightarrow{\mathbb{R}}^{2}$ , natomiast $u:[0,T]\rightarrow{\mathbb{R}}$ . Czy układ (10.1) wraz z równaniem $y(t)=x^{1}+x^{2}+u$ jest wówczas obserwowalny dla

$A=\left[\begin{array}[]{ll}1&1\\ 0&2\\ \end{array}\right],$ $B=\left[\begin{array}[]{l}0\\ 1\\ \end{array}\right]\,?$

Ćwiczenie 10.6

Na ciało o masie $m$ , poruszające się w środowisku bez tarcia, działa zmienna w czasie siła $u(t)$ . Należy zbadać obserwowalność całkowitą tego układu, gdy wielkością wyjściową jest

1) przebyta przez ciało droga,

2) prędkość tego ciała.

10.3. Sterowania bang-bang

Ćwiczenie 10.7

Niech $x:[0,T]\rightarrow{\mathbb{R}}^{2}$ , natomiast $u:[0,T]\rightarrow{\mathbb{R}}$ . Dodatkowo niech $A=\left[\begin{array}[]{ll}1&1\\ 0&2\\ \end{array}\right]$ i $B=\left[\begin{array}[]{l}0\\ 1\\ \end{array}\right]$ . Znaleźć sterowanie bang-bang układu (10.1) ze stanu początkowego $x_{0}\in{\mathbb{R}}^{2}$ do stanu końcowego wynoszącego $0$ w czasie $t_{0}$ .

10.4. Sterowalność ukladów nieliniowych — rozdział 4

Ćwiczenie 10.8

Rozważmy układ równań

$\begin{array}[]{lll}\dot{x}^{1}&=&-2(x^{1})^{3}+2x^{1}x^{2}+u^{1}\,,\\ \dot{x}^{2}&=&-6x^{2}+(x^{1})^{2}+u^{2}\,,\end{array}$

gdzie $x^{1}(t)$ , $x^{2}(t)$ to funkcje o wartościach rzeczywistych, podobnie sterowania $u^{1},u^{2}$ mogą przyjmować wartości rzeczywiste. Czy możliwe jest lokalne i globalne sterowanie $x(t)=\left[\begin{array}[]{ll}x^{1}(t)\\ x^{2}(t)\\ \end{array}\right]$ do $0$ za pomocą wektora sterowań $u(t)=\left[\begin{array}[]{ll}u^{1}(t)\\ u^{2}(t)\\ \end{array}\right]\;$ ?

Ćwiczenie 10.9

Rozważmy układ równań

$\begin{array}[]{lll}\dot{x}^{1}&=&-e^{{x^{1}}}-2x^{1}e^{{{x}^{2}-1}}+1-(u^{1})^{2}-u^{2}\,,\\ \dot{x}^{2}&=&-(x^{1})^{2}e^{{x^{2}-1}}-u^{1}\,,\end{array}$

gdzie $x^{1}(t),x^{2}(t)$ to funkcje o wartościach rzeczywistych, podobnie sterowania $u^{1},u^{2}$ mogą przyjmować wartości rzeczywiste. Czy możliwe jest lokalne i globalne sterowanie $x(t)=\left[\begin{array}[]{ll}x^{1}(t)\\ x^{2}(t)\\ \end{array}\right]$ do $0$ za pomocą wektora sterowań $u(t)=\left[\begin{array}[]{ll}u^{1}(t)\\ u^{2}(t)\\ \end{array}\right]\;$ ?

10.5. Zasada maksimum — rozdziały 7, 9

Ćwiczenie 10.10

Rozważyć układ o równaniach stanu

$\dot{x}^{1}=x^{2}+u^{1},\;\;\dot{x}^{2}=-x^{1}+u^{2}$

gdzie wartości sterowań $u^{1},u^{2}$ są ograniczone do zbioru $[-1,1]$ . Przedyskutować sterowanie czasooptymalne przejścia od $(x^{1}(0),x^{2}(0))$ do $0$ .

Ćwiczenie 10.11

Rozważyć układ o równaniach stanu

$\dot{x}^{i}=x^{{i+3}},\;\;\dot{x}^{{i+3}}=u^{i}$

dla $i=1,2,3$ , gdzie wartości sterowań $u^{i}$ podlegają więzom $0\leq\sum\limits _{{i=1}}^{3}(u^{i})^{2}\leq 1$ . Przedyskutować sterowanie czasooptymalne przejścia od $(x^{1}(0),x^{2}(0),...,x^{6}(0))$ do $0$ .

Ćwiczenie 10.12

Rozważyć układ o równaniach stanu

$\dot{x}^{1}=x^{2}+u,\;\;\dot{x}^{2}=-u$

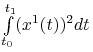gdzie wartości sterowań $u^{1},u^{2}$ są ograniczone do zbioru $[-1,1]$ . Chcemy przeprowadzić ten układ z $(x^{1}(0),x^{2}(0))$ do $0$ minimalizując funkcjonał $\int\limits _{{t_{0}}}^{{t_{1}}}(x^{1}(t))^{2}dt$ . Przedyskutować sterowanie ekstremalne.

Ćwiczenie 10.13

Następujące równania stanu oddają opis zachowania się samolotu w locie płaskim

$\begin{array}[]{lll}\dot{x}^{1}&=&x^{2}u\,,\\ \dot{x}^{2}&=&F(x^{1},x^{2})-u\,,\end{array}$

gdzie $F$ jest funkcją klasy $C^{1}$ , sterowanie $u$ spełnia $|u|\leq 1$ . Chcemy przeprowadzić układ ze stanu $(x^{1}(0),x^{2}(0))$ do stanu $(x_{1}^{1},x_{1}^{2})$ minimalizując czas przejścia. Przedyskutować sterowanie ekstremalne.

Ćwiczenie 10.14

Następujące równania opisują zachowanie się rakiety w prostoliniowym locie poziomym pod wpływem sił ciężkości

$\dot{x}^{1}=x^{2},\;\;\dot{x}^{2}=u\,,$

gdzie sterowanie $u\in[-1,1]$ . Chcemy minimalizować zużycie paliwa $\int _{{t_{0}}}^{{t_{1}}}\sqrt{(1+(u)^{2}(t))}dt$ przy przejściu układu ze stanu $(x^{1}(0),x^{2}(0))$ do $0$ . Przedyskutować sterowanie optymalne.

Ćwiczenie 10.15

Równania ruchu prostoliniowego rakiety o stałej mocy dane są układem równań

$\dot{x}^{1}=u,\;\;\dot{x}^{2}=(u)^{2}.$

Sterowanie jest znormalizowane przez warunek $|u|\leq 1$ . Znaleźć sterowanie czasooptymalne przejścia układu ze stanu $(x^{1}(0),x^{2}(0))$ do stanu $(x_{1}^{1},x_{1}^{2})$ , czy takie sterowania są w tym przypadku jednoznaczne?

10.6. Przykłady

Przykład 10.1

(czasooptymalny problem nawigacji, [42]). Przedyskutujmy teraz klasyczne zagadnienie teorii sterowania. Nawigujemy łódką o prędkości $v$ , takiej że $|v|=1$ niezależnie od czasu. Woda płynie ze stałą prędkością $s$ . Chcemy dostać się do ustalonego punktu w jak najkrótszym czasie. Zagadnienie rozpatrujemy w dwuwymiarowej płaszczyźnie $x_{1},x_{2}$ , gdzie osie są dobrane tak, by przepływ był prostopadły do jednej ( $x_{1}$ ), a równoległy do drugiej ( $x_{2}$ ). Niech kąt sterowania pomiędzy $s$ i $v$ będzie oznaczany przez $\psi$ . Równania ruchu statku mają postać

$\dot{x_{1}}=s+\cos\psi,\;\;\dot{x_{2}}=\sin\psi.$

(10.2)

Równoważnie

$\dot{x_{1}}=s+u_{1},\;\;\dot{x_{2}}=u_{2},$

(10.3)

wraz z więzami sterowania

$u_{1}^{2}+u_{2}^{2}=1.$

(10.4)

Po pierwsze, wykorzystując postać zagadnienia (10.2) można sprawdzić, że założenia twierdzenia 8.1, włącznie z założeniami 8.1, 8.2 są spełnione, czyli spośród sterowań ekstremalnych można wybrać optymalne.

Dzięki postaci (10.3), (10.4) rozważanego zagadnienia posłużymy się teraz zasadą maksimum Pontriagina dla ustalenia sterowań optymalnych.

Hamiltonian dany jest przez $H(\lambda,x,u):=\lambda _{0}+\lambda _{1}(s+u_{1})+\lambda _{2}u_{2}$ , gdzie $(\lambda _{1},\lambda _{2})$ to współrzędne sprzężone. Mamy następujące równania Hamiltona na kostany

$\dot{\lambda _{i}}(t)=0,\;\;,i=1,2.$

Zatem

$\lambda _{i}=\lambda _{i}^{0},\;\;,i=1,2,$

(10.5)

i pszukujemy sterowań, przy których wyrażenie

$\lambda _{1}^{0}u_{1}+\lambda _{2}^{0}u_{2}+\lambda _{0}+\lambda _{1}^{0}s$

osiąga kres górny przy więzach (10.4). Widzimy, że kres górny osiągany jest, gdy wektory $(u_{1},u_{2})$ i $(\lambda _{1}^{0},\lambda _{2}^{0})$ mają ten sam kierunek i zwrot, czyli dla

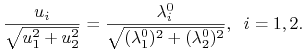$\frac{u_{i}}{\sqrt{u_{1}^{2}+u_{2}^{2}}}=\frac{\lambda _{i}^{0}}{\sqrt{(\lambda _{1}^{0})^{2}+(\lambda _{2}^{0})^{2}}},\;\; i=1,2.$

W świetle (10.4) sterowanie ekstremalne jest dane wzorem

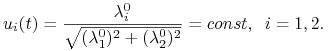$u_{i}(t)=\frac{\lambda _{i}^{0}}{\sqrt{(\lambda _{1}^{0})^{2}+(\lambda _{2}^{0})^{2}}}=const,\;\; i=1,2.$

Widzimy, że sterowanie ekstremalne to takie, dla którego kąt między wektorem prędkości przepływu oraz wektorem prędkości statku jest stały. Mamy zatem jakościowy wniosek, iż trajektorie sterowań ekstremalnych są liniami prostymi. Możemy automatycznie wyznaczyć ewentualny czas przejścia naszej łódki $\tau$ . Otóż

$\tau^{2}(1-s^{2})+2(x_{1}^{{end}}-x_{1}(0))s\tau-(x_{1}^{{end}}-x_{1}(0))^{2}-(x_{2}^{{end}}-x_{2}(0))^{2}=0.$

(10.6)

Ponadto dla danej wartości czasu $\tau$ sterowanie ekstremalne jest jednoznaczne, dane przez

$u_{1}(t)=\frac{x_{1}^{{end}}-x_{1}(0)-\tau s}{\tau},\;\; u_{2}(t)=\frac{x_{2}^{{end}}-x_{2}(0)}{\tau}.$

Wyznaczmy teraz najlepsze spośród sterowań ekstremalnych, będące optymalnym sterowaniem w problemie nawigacji. W tym celu rozróżniamy trzy przypadki.

Przypadek pierwszy, $s<1$ . Uwzględniając warunek $\tau\geq 0$ , wobec (10.6) mamy

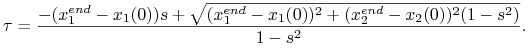$\tau=\frac{-(x_{1}^{{end}}-x_{1}(0))s+\sqrt{(x_{1}^{{end}}-x_{1}(0))^{2}+(x_{2}^{{end}}-x_{2}(0))^{2}(1-s^{2})}}{1-s^{2}}.$

Widać, że jest tylko jedno sterowanie ekstremalne, zatem istnieje tor optymalny niezależnie od punktów, w których zaczynamy i kończymy nawigację.

Przypadek drugi, $s=1$ . Tutaj rozwiązanie (10.6) to

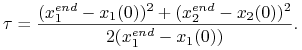$\tau=\frac{(x_{1}^{{end}}-x_{1}(0))^{2}+(x_{2}^{{end}}-x_{2}(0))^{2}}{2(x_{1}^{{end}}-x_{1}(0))}.$

Znów mamy tylko jedno sterowanie ekstremalne, zatem jednocześnie optymalne. Tym razem jednak wobec warunku $\tau\geq 0$ od razu widać, że $(x_{1}^{{end}}-x_{1}(0))>0$ , co zawęża zbór punktów początkowych oraz końcowych, pomiędzy którymi możemy nawigować. Musi zachodzić $x_{1}^{{end}}>x_{1}(0)$ .

Przypadek trzeci, $s<1$ . Tutaj (10.6) ma dwa pierwiastki. Naturalnie ten o większej wielkości nie jest czasem przepływu odpowiadającym sterowaniu optymalnemu. Zatem sterowanie optymalne jest realizowalne w czasie

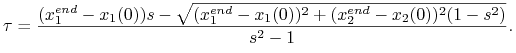$\tau=\frac{(x_{1}^{{end}}-x_{1}(0))s-\sqrt{(x_{1}^{{end}}-x_{1}(0))^{2}+(x_{2}^{{end}}-x_{2}(0))^{2}(1-s^{2})}}{s^{2}-1}.$

Uwzględnienie warunku $\tau\geq 0$ prowadzi tym razem do wniosku, iż punkty $(x_{1}(0),x_{2}(0))$ , z których optymalna nawigacja jest wykonalna zajdują się w prawej części płaszczyzny oraz w lewej na prawo od półprostych przechodzących przez punkt $(x_{1}(0),x_{2}(0))$ , takich że ich współczynniki kierunkowe dane są przez liczby $-(s-1)^{{\frac{1}{2}}}$ i $(s-1)^{{\frac{1}{2}}}$ .

Przykład 10.2

(Leitman, maksymalny zasięg rakiety o ograniczonym ciągu przy zaniedbaniu aerodynamiki) Naszym celem będzie znalezienie ekstremalnych sterowań maksymalizujących zasięg rakiety o ciągach nie przekraczających określonej wartości. Ustalając model matematyczny zjawiska przyjmiemy, że jesteśmy w stałym (ziemskim) polu grawitacyjnym. Ograniczymy się do badania lotu płaskiego. Dodatkowo zaniedbamy zjawiska aerodynamiczne. W ten sposób dostaniemy model, który z jednej strony dzięki swojej prostocie umożliwi nam analizę. Z drugiej jednak będziemy pamiętać, że chcąc dostać wyniki wartościowe z punktu widzenia praktyki uwzględnić trzeba chociażby siłę nośną jaka wpłynie na rakietę.

Rozpatrujemy proces we współrzędnych kartezjańskich $x_{1},x_{2}$ . Składowe prędkości $\dot{x_{1}},\dot{x_{2}}$ będziemy często oznaczać przez $x_{3},x_{4}$ . Masę rakiety oznaczać będziemy przez $x_{5}(t)$ , jest ona funkcją czasu. Zależy od ilości paliwa w zbiorniku. Przyspieszenie ziemskie to $g$ , natomiast $u_{1}$ i $u_{2}$ oznaczają kosinusy kierunkowe wektora ciągu. Prędkość wypływu masy będziemy oznaczać przez przez $u_{3}:=\dot{x_{3}}$ . Skuteczną prędkość wylotu spalin będziemy oznaczać przez $c$ , jest to dodatnia stała.

Z jednej strony na rakietę działa ściągająca ją w dół siła grawitacji, z drugiej prowadząca ją siła ciągu równa co do wartości $cu_{3}$ , a działająca pod kątem $\Psi$ do osi $Ox_{1}$ . Wtedy $u_{1}=\cos\Psi$ , a $u_{2}=\sin\Psi$ .

Wówczas stan układu opisany jest równaniami:

$\dot{x_{1}}=x_{3},$

$\dot{x_{2}}=x_{4},$

$\dot{x_{3}}=\frac{c}{x_{5}}u_{1}u_{3},$

(10.7)

$\dot{x_{4}}=\frac{c}{x_{5}}u_{2}u_{3}-g,$

(10.8)

$\dot{x_{5}}=-u_{3}.$

(10.9)

Jak zaznaczyliśmy, cią jest ograniczony, zatem $0\leq cu_{3}\leq cu_{3}^{{max}}$ . Mamy wobec tego pierwsze więzy

$0\leq u_{3}\leq u_{3}^{{max}}.$

(10.10)

Dodatkowo, wobec jedynki trygonometrycznej,

$u_{1}^{2}+u_{2}^{2}=1.$

(10.11)

Nasze zagadnienie dotyczy przeniesienia rakiety o danych masie i prędkości początkowej z punktu $(x_{1}(0),x_{2}(0))$ do położenia o danej wyskości $h$ przy użyciu ograniczonej ilości paliwa. Przy czym zależy nam na maksymalnym zasięgu. Nasze sterowanie to zmienne $u_{i}$ dla $i=1,2,3$ , czyli kąt ustawienia rakiety oraz prędkość wypływu masy. Przeprowadzamy układ z punktu $(x_{1}(0),...,x_{5}(0))$ do miejsca określonego przez

$x_{2}=x_{2}^{{end}},\;\; x_{5}=x_{5}^{{end}}>0.$

Dodatkowo minimalizujemy funkcjonał kosztu

$-\int _{0}^{{t_{1}}}x_{3}(s)ds.$

(10.12)

Użyjemy zasady maksimum Pontriagina. Naszym hamiltonianem będzie

$H(\lambda,x,u)=u_{3}\left[\frac{c}{x_{5}}(\lambda _{1}u_{1}+\lambda _{4}u_{2})-\lambda _{5}\right]-\lambda _{0}x_{3}+\lambda _{1}x_{3}+\lambda _{2}x_{4}-\lambda _{4}g.$

Wobec sformułowania zagadnienia kostany spełniają równanie

$\dot{\lambda _{1}}=\dot{\lambda _{2}}=0,$

$\dot{\lambda _{3}}=\lambda _{0}-\lambda _{1},\;\;\dot{\lambda _{4}}=-\lambda _{2},$

$\dot{\lambda _{5}}=\frac{cu_{3}}{x_{5}^{2}}(\lambda _{1}u_{1}+\lambda _{4}u_{2}).$

Wykonujemy oczywiste całkowania i mamy

$\lambda _{1}(t)=\lambda _{1}(t_{1}),\;\;\lambda _{2}(t)=\lambda _{2}(t_{1}),\;\;\lambda _{3}(t)=(\lambda _{1}(t_{1})-\lambda _{0})(t_{1}-t)+\lambda _{3}(t_{1}),$

$\lambda _{4}(t)=\lambda _{2}(t_{1})(t_{1}-t)+\lambda _{4}(t_{1}).$

Teraz warunek (iv) twierdzenia 9.3 mówi nam, że

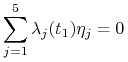$\sum _{{j=1}}^{5}\lambda _{j}(t_{1})\eta _{j}=0$

dla wszystkich rzeczywistych liczb $\eta _{j},j=1,...,5$ takich że $\eta _{2}=\eta _{5}=0$ . Mamy zatem

$\lambda _{1}(t_{1})=\lambda _{3}(t_{1})=\lambda _{4}(t_{1})=0.$

A wówczas

$\lambda _{1}(t)=0,\;\;\lambda _{2}(t)=\lambda _{2}(t_{1}),$

(10.13)

$\lambda _{3}(t)=-\lambda _{0}(t_{1}-t),\;\;\lambda _{4}(t)=\lambda _{2}(t_{1})(t_{1}-t).$

(10.14)

Wobec (i) twierdzenia 9.3 wiemy, że sterowanie ekstremalne jest takie, że związana z nim odpowiedź maksymalizuje hamiltonian dla dowolnego kostanu $\lambda$ . Zatem musimy dobrać sterowanie $u$ takie, aby zależna od niego część hamiltonianu

$u_{3}\left[\frac{c}{x_{5}(t)}(\lambda _{1}(t)u_{1}(t)+\lambda _{4}(t)u_{2}(t))-\lambda _{5}(t)\right]$

(10.15)

przyjmowała wartość najwięszą.

Wyznaczymy sterowania ekstremalne przy założeniu, że $u_{3}(t)\neq 0$ dla $0\leq t\leq t_{1}$ . Wówczas (10.15) przyjmuje wartość maksymalną w sytuacji, gdy wektor $(\lambda _{1},\lambda _{2})$ jest równoległy do $(u_{1},u_{2})$ i mają one taki sam zwrot. Dodatkowo, z (10.11) wiemy, że w takim razie

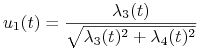$u_{1}(t)=\frac{\lambda _{3}(t)}{\sqrt{\lambda _{3}(t)^{2}+\lambda _{4}(t)^{2}}}$

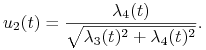$u_{2}(t)=\frac{\lambda _{4}(t)}{\sqrt{\lambda _{3}(t)^{2}+\lambda _{4}(t)^{2}}}.$

Następnie (10.14) implikuje $\lambda _{3}(t)^{2}+\lambda _{4}(t)^{2}=(t_{1}-t)^{2}(\lambda _{0}^{2}+\lambda _{2}(t)^{2})$ , natomiast (10.13) daje $\lambda _{2}(t)=\lambda _{2}(t_{1})$ dla każdego $0\leq t\leq t_{1}$ . Zatem

$u_{1}(t)=\frac{-\lambda _{0}}{\sqrt{\lambda _{0}^{2}+\lambda _{2}^{2}(t_{1})}}=const,$

(10.16)

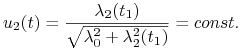$u_{2}(t)=\frac{\lambda _{2}(t_{1})}{\sqrt{\lambda _{0}^{2}+\lambda _{2}^{2}(t_{1})}}=const.$

(10.17)

Czyli kąt między rakietą, a $Ox_{1}$ jest stały.

Pozostaje jeszcze kwestia wielkości ciągu ekstremalnego $cu_{3}(t)$ . Nie będziemy tu jej rozważać.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Teoria sterowania

Zagadnienia

10. Zadania

10.1. Sterowalność — rozdział 2

Definicja 10.1

Ćwiczenie 10.1

Ćwiczenie 10.2

Ćwiczenie 10.3

Ćwiczenie 10.4

10.2. Obserwowalność — rozdział 3

Ćwiczenie 10.5

Ćwiczenie 10.6

10.3. Sterowania bang-bang

Ćwiczenie 10.7

10.4. Sterowalność ukladów nieliniowych — rozdział 4

Ćwiczenie 10.8

Ćwiczenie 10.9

10.5. Zasada maksimum — rozdziały 7, 9

Ćwiczenie 10.10

Ćwiczenie 10.11

Ćwiczenie 10.12

Ćwiczenie 10.13

Ćwiczenie 10.14

Ćwiczenie 10.15

10.6. Przykłady

Przykład 10.1

Przykład 10.2