2. Sterowalność
Współrzędne wektora ![]() oznaczamy
oznaczamy ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
![x=\left[\begin{array}[]{c}x^{1}\\
.\\
.\\
.\\
x^{n}\end{array}\right]\,.](wyklady/tst/mi/mi161.png) |
Dla odróżnienia naturalne potęgi ![]() oznaczamy jako
oznaczamy jako ![]() ,
, ![]() .
.
Dla uproszczenia notacji element zerowy w każdej ![]() , dla
, dla ![]() ,
oznaczamy przez
,
oznaczamy przez ![]() .
.
Definicja 2.1
Niech ![]() ,
, ![]() będzie zadanym zbiorem. Zbiór ten będziemy nazywali
zbiorem parametrów sterujących.
będzie zadanym zbiorem. Zbiór ten będziemy nazywali
zbiorem parametrów sterujących.
Przez większą część wykładu, będziemy przyjmować, że ![]() ,
choć omówimy kilkakrotnie sytuacje
,
choć omówimy kilkakrotnie sytuacje ![]() .
Jeżeli nie będzie podane inaczej, będziemy zakładali, że
.
Jeżeli nie będzie podane inaczej, będziemy zakładali, że ![]() .
Niech
.
Niech
Każdy element ![]() będziemy nazywali sterowaniem (control)
(lub strategią).
Dla każdego sterowania
będziemy nazywali sterowaniem (control)
(lub strategią).
Dla każdego sterowania ![]() istnieje odpowiedni odcinek
istnieje odpowiedni odcinek ![]() , na którym jest określone.
, na którym jest określone.
Definicja 2.2
Dla każdego ![]() określamy rodzinę zbiorów celu (target sets)
określamy rodzinę zbiorów celu (target sets)
![]() , gdzie
, gdzie ![]() jest zbiorem domkniętym w
jest zbiorem domkniętym w ![]() .
.
Rozpatrujemy zagadnienie początkowe dla równania różniczkowego zwyczajnego
| (2.1) |
gdzie ![]() ,
, ![]() oraz
oraz ![]() ,
, ![]() ,
jest poszukiwanym sterowaniem.
,
jest poszukiwanym sterowaniem.
Powyższe zagadnienie dotyczy sterowania w pętli otwartej (control in open–loop form),
![]() . Można też rozpatrywać sterowanie w zamkniętej
pętli (control in closed–loop form), gdy poszukuje się odwzorowania (zwanego
sprzężeniem zwrotnym (feedback)
. Można też rozpatrywać sterowanie w zamkniętej
pętli (control in closed–loop form), gdy poszukuje się odwzorowania (zwanego
sprzężeniem zwrotnym (feedback)
![]() dla RRZ
dla RRZ
| (2.2) |
Sprowadzenie ![]() do
do ![]() nazywa się zagadnieniem syntezy (synthesis)
sterowania.
nazywa się zagadnieniem syntezy (synthesis)
sterowania.
Możliwe jest podejście alternatywne w języku inkluzji różniczkowej (differential inclusion)
| (2.3) |
gdzie
Założenie 2.1
Funkcja
jest ciągła wraz z pochodnymi cząstkowymi ![]() ,
,
![]() dla
dla ![]() ,
, ![]() na
zbiorze
na
zbiorze ![]() .
.
Założenie 2.1 gwarantuje lokalne istnienie i
jednoznaczność rozwiązania dla ![]() — tw. Picarda–Lindelöfa — por.
[14, 17, 23]. Ponieważ jednak funkcja
— tw. Picarda–Lindelöfa — por.
[14, 17, 23]. Ponieważ jednak funkcja ![]() jest jedynie funkcją mierzalną i ograniczoną, więc
prawa strona RRZ (2.1) jest tylko mierzalna i ograniczona jako funkcja
jest jedynie funkcją mierzalną i ograniczoną, więc
prawa strona RRZ (2.1) jest tylko mierzalna i ograniczona jako funkcja ![]() dla
każdego
dla
każdego ![]() . Zatem rozwiązanie rozumiane jest jako absolutnie ciągła funkcja spełniająca
RRZ (2.1) prawie wszędzie — por. [14, 17, 23].
. Zatem rozwiązanie rozumiane jest jako absolutnie ciągła funkcja spełniająca
RRZ (2.1) prawie wszędzie — por. [14, 17, 23].
Założenie 2.1 jest mocniejsze, niż jest to jest potrzebne w niektórych wynikach. Do istnienia i jednoznaczności wystarczy Lipschitz–owskość, ciągłość też można osłabić.
Definicja 2.3
Dla zadanego sterowania ![]() rozwiązanie RRZ (2.1) nazywa się
odpowiedzią na (response to)
rozwiązanie RRZ (2.1) nazywa się
odpowiedzią na (response to) ![]() — oznaczamy
— oznaczamy
![]() .
.
Problem 2.1
Zagadnienie sterowania (control problem): dla zadanego ![]() znaleźć
znaleźć ![]() oraz
oraz ![]() , t.ż. odpowiednia odpowiedź
, t.ż. odpowiednia odpowiedź
![]() .
.
Jeżeli takie ![]() da się znaleźć, to mówimy, że sterowanie
da się znaleźć, to mówimy, że sterowanie ![]() prowadzi
prowadzi ![]() do celu
do celu ![]() (control
(control ![]() steers
steers ![]() to the target
to the target ![]() ), lub że
), lub że ![]() jest
sterowaniem pomyślnym (successful control).
jest
sterowaniem pomyślnym (successful control).
Problem 2.2
Zagadnienie sterowalności (controllability
problem):
określić dane początkowe, które można doprowadzić do celu (tzn. dane początkowe, które są
sterowalne (controllable)), czyli określić te dane
początkowe, dla których istnieje pomyślne sterowanie ![]() .
.
Definicja 2.4
Zbiór sterowalny (controllable set)
![]() , gdzie
, gdzie
| (2.4) |
![]() jest zbiorem tych stanów, które mogą być doprowadzone do celu
w chwili
jest zbiorem tych stanów, które mogą być doprowadzone do celu
w chwili ![]() .
.
Będziemy badali zbiór ![]() , oraz określimy jak zmienia się
, oraz określimy jak zmienia się ![]() wraz z zawężeniem klasy sterowań.
wraz z zawężeniem klasy sterowań.
Definicja 2.5
Jeżeli ![]() , to sterowalność jest całkowita (completely
controllable). Natomiast przypadek
, to sterowalność jest całkowita (completely
controllable). Natomiast przypadek ![]() nazywamy sterowalnością
lokalną (locally controllable).
nazywamy sterowalnością
lokalną (locally controllable).
Można rozważać węższe klasy sterowań (por. [31]):
-
Klasa sterowań kawałkami stałych (piecewise constant controls)
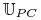 :
:![u\in{{\mathbb{U}}}_{{PC}}[0,{{t_{1}}}]](wyklady/tst/mi/mi233.png) , jeżeli
, jeżeli 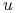 jest kawałkami stała na
jest kawałkami stała na
![[0,{{t_{1}}}]](wyklady/tst/mi/mi13.png) , czyli istnieją
, czyli istnieją 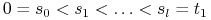 , t. ż,
, t. ż, 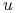 jest stała na każdym
przedziale
jest stała na każdym
przedziale 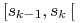 ;
;![{{\mathbb{U}}}_{{PC}}=\bigcup\limits _{{{{t_{1}}}>0}}\;{{\mathbb{U}}}_{{PC}}[0,{{t_{1}}}]\,.](wyklady/tst/mi/mi208.png)
-
Klasa sterowań gładkich i niezmieniających się nagle (smooth controls that do not change rapidly)
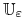 :
:![u\in{{\mathbb{U}}}_{{\varepsilon}}[0,{{t_{1}}}]](wyklady/tst/mi/mi333.png) , jeżeli
, jeżeli 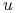 jest absolutnie
ciągła na
jest absolutnie
ciągła na ![[0,{{t_{1}}}]](wyklady/tst/mi/mi13.png) ,
, 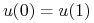 oraz
oraz 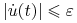 p.w. na
p.w. na
![[0,{{t_{1}}}]\,](wyklady/tst/mi/mi50.png) ;
;![{{\mathbb{U}}}_{{\varepsilon}}=\bigcup\limits _{{{{t_{1}}}>0}}\;{{\mathbb{U}}}_{{\varepsilon}}[0,{{t_{1}}}]\,.](wyklady/tst/mi/mi157.png)
-
Klasa sterowań ,,bang–bang” (bang–bang controls)
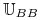 :
:![u\in{{\mathbb{U}}}_{{BB}}[0,{{t_{1}}}]](wyklady/tst/mi/mi188.png) , jeżeli
, jeżeli 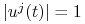 dla p.k.
dla p.k. ![t\in[0,{t_{1}}]\,](wyklady/tst/mi/mi206.png) oraz każdego
oraz każdego 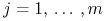 ;
;![{{\mathbb{U}}}_{{BB}}=\bigcup\limits _{{{{t_{1}}}>0}}\;{{\mathbb{U}}}_{{BB}}[0,{{t_{1}}}]\,.](wyklady/tst/mi/mi75.png)
-
Klasa sterowań bang–bang kawałkami stałych
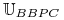 :
:![{{\mathbb{U}}}_{{BBPC}}[0,{{t_{1}}}]={{\mathbb{U}}}_{{BB}}[0,{{t_{1}}}]\bigcap{{\mathbb{U}}}_{{PC}}[0,{{t_{1}}}]\,;](wyklady/tst/mi/mi398.png)
![{{\mathbb{U}}}_{{BBPC}}=\bigcup\limits _{{{{t_{1}}}>0}}\;{{\mathbb{U}}}_{{BBPC}}[0,{{t_{1}}}]\,.](wyklady/tst/mi/mi66.png)
Analogicznie do ![]() określamy zbiory sterowalne
określamy zbiory sterowalne ![]() ,
, ![]() ,
,
![]() ,
, ![]() w odniesieniu do odpowiednich klas sterowań.
w odniesieniu do odpowiednich klas sterowań.
Problem 2.3
Rozpatrywać będziemy ogólne autonomiczne (autonomous) zagadnienie nieliniowe (NLA)
| (2.5) |
z warunkiem początkowym
i celem ![]() .
.
Założenie 2.2
Zakładamy, że funkcja ![]() jest klasy
jest klasy ![]() na
na ![]() oraz
oraz ![]() .
.
Stąd dla zadanego warunku początkowego ![]() odpowiedź
odpowiedź ![]() istnieje
(przynajmniej) lokalnie w czasie i jest jednoznaczna.
istnieje
(przynajmniej) lokalnie w czasie i jest jednoznaczna.
Będziemy również rozpatrywać zagadnienie liniowe (LA)
Problem 2.4
| (2.6) |
gdzie ![]() i
i ![]() są stałymi macierzami,
są stałymi macierzami, ![]() i
i ![]() , odpowiednio,
, odpowiednio,
z warunkiem początkowym
i celem ![]() .
.
Macierz ![]() ma więc postać:
ma więc postać:
![B=\left[\begin{array}[]{ccc}b_{{11}}&\ldots&b_{{1m}}\\
.&.&.\\
.&.&.\\
.&.&.\\
b_{{n1}}&\ldots&b_{{nm}}\end{array}\right]\,.](wyklady/tst/mi/mi184.png) |
Lemat 2.1
Dla (NLA):
-
Jeżeli
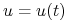 prowadzi
prowadzi 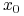 do
do 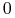 na
na ![[0,{t_{1}}]](wyklady/tst/mi/mi211.png) z odpowiedzią
z odpowiedzią 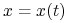 (tzn.
(tzn.
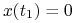 ), to
), to 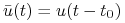 prowadzi
prowadzi 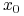 do
do 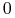 na
na ![[t_{0},t_{0}+{t_{1}}]](wyklady/tst/mi/mi128.png) z odpowiedzią
z odpowiedzią
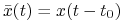 .
. -
Jeżeli
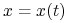 jest odpowiedzią na
jest odpowiedzią na ![u\in{\mathbb{U}}_{m}[0,{t_{1}}]](wyklady/tst/mi/mi273.png) prowadzącą
prowadzącą 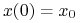 do
do 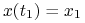 , to
, to 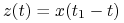 jest odpowiedzią na
jest odpowiedzią na 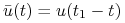 dla równania (z odwróconym czasem)
dla równania (z odwróconym czasem)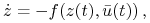
(2.7) prowadzącą
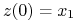 do
do 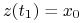 .
.
Dowód
![]()
1. Mamy
dla p.w. ![]() . Ponadto
. Ponadto
2. Mamy
dla p.w. ![]() . Ponadto
. Ponadto
Zagadnienie (NLA) jest autonomiczne w tym sensie, że punkt 1 lematu 2.1 jest spełniony.
Definicja 2.6
Zbiór jest łukowo spójny (arcwise connected), jeżeli każde dwa punkty zbioru mogą być połączone łukiem (homeomorficznym obrazem odcinka) całkowicie zawartym w zbiorze.
Twierdzenie 2.1
Dla (NLA):
-
jeżeli
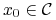 oraz
oraz 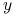 jest punktem trajektorii łączącej
jest punktem trajektorii łączącej 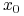 z celem
z celem 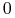 ,
to
,
to 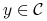 ;
; -
zbiór
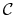 jest łukowo spójny;
jest łukowo spójny; -
jeżeli
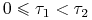 , to
, to 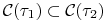 ;
; -
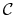 jest otwarty wtedy i tylko wtedy, gdy
jest otwarty wtedy i tylko wtedy, gdy 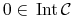 .
.
Dowód: [31] — str. 26–27, [24] — str. 31–32.
![]()
1. Niech ![]() . Istnieje wówczas pomyślne sterowanie
. Istnieje wówczas pomyślne sterowanie ![]() oraz odpowiedź
oraz odpowiedź
![]() , t.ż.
, t.ż. ![]() dla pewnego
dla pewnego ![]() . Dla
. Dla ![]() chcemy pokazać, że
chcemy pokazać, że ![]() . Sterowanie
. Sterowanie ![]() ,
określone na
,
określone na ![]() jest pomyślne z odpowiedzią
jest pomyślne z odpowiedzią
![]() :
:
a zatem ![]() .
.
2. Jeżeli ![]() ,
, ![]() są w
są w ![]() , to istnieją sterowania
, to istnieją sterowania ![]() i
i ![]() oraz
odpowiedzi
oraz
odpowiedzi ![]() ,
, ![]() ,
t.ż.
,
t.ż.
Z 1. każdy punkt obu trajektorii jest w ![]() . Zatem istnieje łuk całkowicie
zawarty w
. Zatem istnieje łuk całkowicie
zawarty w ![]() łączący punkty
łączący punkty ![]() ,
, ![]() .
.
3. Niech ![]() . Zatem istnieje sterowanie
. Zatem istnieje sterowanie ![]() , t.ż.
, t.ż. ![]() dla
odpowiedzi
dla
odpowiedzi ![]() . Dla
. Dla ![]() określmy sterowanie
określmy sterowanie
Z warunku ![]() wynika, że odpowiedż
wynika, że odpowiedż ![]() spełnia
spełnia
a zatem ![]() prowadzi
prowadzi ![]() do celu
do celu ![]() w czasie
w czasie ![]() , czyli
, czyli ![]() .
.
4. Implikacja ,,![]() ” jest oczywista, gdyż
” jest oczywista, gdyż ![]() .
.
Pokażemy implikację ,,![]() ”. Jeżeli
”. Jeżeli ![]() , to istnieje otwarta kula
, to istnieje otwarta kula
![]() o środku w
o środku w ![]() i promieniu
i promieniu ![]() ,
t.ż.
,
t.ż. ![]() .
Niech
.
Niech ![]() . Chcemy pokazać, że istnieje otwarta kula o środku w
. Chcemy pokazać, że istnieje otwarta kula o środku w ![]() całkowicie
zawarta w
całkowicie
zawarta w ![]() . Ponieważ
. Ponieważ ![]() , więc istnieje sterowanie
, więc istnieje sterowanie ![]() oraz
odpowiedź
oraz
odpowiedź ![]() , t.ż.
, t.ż. ![]() dla pewnego
dla pewnego ![]() .
Funkcja
.
Funkcja ![]() jest klasy
jest klasy ![]() , więc z ciągłej zależności od danych początkowych wynika istnienie
otwartej kuli
, więc z ciągłej zależności od danych początkowych wynika istnienie
otwartej kuli ![]() ,
, ![]() ,
t.ż. dla każdego
,
t.ż. dla każdego ![]() :
:
Istnieje więc sterowanie ![]() , które prowadzi
, które prowadzi ![]() do
do ![]() w czasie
w czasie
![]() .
.
Zatem dla każdego ![]() istnieje sterowanie
istnieje sterowanie ![]() ,
,
| (2.8) |
które prowadzi ![]() do
do ![]() . Zatem
. Zatem ![]() .
.
Uwaga 2.1
Można pokazać, że są prawdziwe twierdzenia analogiczne do twierdzenia 2.1 dla
klas ![]() oraz
oraz ![]() . Dla
. Dla ![]() oraz
oraz ![]() punkty 1, 2 i 4 wynikają bezpośrednio. Natomiast punkt 3 dla
punkty 1, 2 i 4 wynikają bezpośrednio. Natomiast punkt 3 dla ![]() wynika z
zasady bang–bang — por. twierdzenie 5.1.
wynika z
zasady bang–bang — por. twierdzenie 5.1.
Uwaga 2.2
Argumentu w dowodzie ,,![]() ” punktu 4 twierdzenia 2.1 nie można
przenieść na
” punktu 4 twierdzenia 2.1 nie można
przenieść na ![]() dla
dla ![]() , gdyż sterowanie (2.8) określone jest
na
, gdyż sterowanie (2.8) określone jest
na ![]() . Najczęściej brzeg zbioru
. Najczęściej brzeg zbioru ![]() należy do tego zbioru,
więc
należy do tego zbioru,
więc ![]() nie jest otwarty.
nie jest otwarty.
Rozważymy teraz zagadnienie liniowe (LA). Rozwiązanie (LA) ma postać
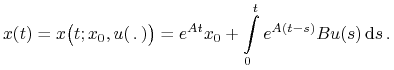 |
(2.9) |
Mamy:
![x_{0}\in{\mathcal{C}}({t_{1}})\quad\Leftrightarrow\quad\exists\; u\in{\mathbb{U}}_{m}[0,{t_{1}}]\;:\quad x_{0}=-\int\limits _{0}^{{t_{1}}}e^{{-As}}Bu(s)\,{\mathrm{d}}s\,,](wyklady/tst/mi/mi200.png) |
(2.10) |
Definicja 2.7
Zbiór ![]() jest symetryczny (symmetric), gdy
jest symetryczny (symmetric), gdy ![]()
![]()
![]() .
.
Twierdzenie 2.2
Dla (LA): ![]() jest symetryczny oraz wypukły.
jest symetryczny oraz wypukły.
Dowód: [19] — str. 17, [31] — str. 29, [24] — str. 33.
![]()
Mamy (2.10).
Jeżeli ![]() dla
dla ![]() , to
, to ![]() dla
dla
![]() . Zatem
. Zatem ![]() jest symetryczny.
jest symetryczny.
Jeżeli ![]() ze sterowaniem
ze sterowaniem ![]() i
i ![]() ze sterowaniem
ze sterowaniem ![]() ,
to
,
to ![]() ze sterowaniem
ze sterowaniem ![]() .
Zatem
.
Zatem ![]() jest wypukły. Nie wynika z tego od razu, że
jest wypukły. Nie wynika z tego od razu, że
![]() jest wypukły
(suma zbiorów wypukłych nie musi być wypukła). Jednakże stosując argument z dowodu punktu 3 twierdzenia 2.1
pokazujemy, że
jest wypukły
(suma zbiorów wypukłych nie musi być wypukła). Jednakże stosując argument z dowodu punktu 3 twierdzenia 2.1
pokazujemy, że ![]() jest wypukły.
jest wypukły.
Twierdzenie 2.2 można uogólnić na sytuację, gdy ![]() ,
, ![]() są ciągłymi
funkcjami. W dowodzie korzysta się z następujących własności klasy sterowań:
symetryczności, wypukłości i możliwości przyjmowania wartości
są ciągłymi
funkcjami. W dowodzie korzysta się z następujących własności klasy sterowań:
symetryczności, wypukłości i możliwości przyjmowania wartości ![]() . Twierdzenie 2.2
zachodzi więc dla klas
. Twierdzenie 2.2
zachodzi więc dla klas ![]() i
i ![]() , ale nie zachodzi dla
, ale nie zachodzi dla
![]() i
i ![]() , które nie są wypukłe i nie zawierają
, które nie są wypukłe i nie zawierają ![]() .
W rozdziale 5 (twierdzenie 5.1) pokażemy jednak zasadę ,,bang–bang”
dla (LA):
.
W rozdziale 5 (twierdzenie 5.1) pokażemy jednak zasadę ,,bang–bang”
dla (LA): ![]() .
Z zasady ,,bang–bang” wynika, że
.
Z zasady ,,bang–bang” wynika, że
a zatem z wypukłości ![]() wynika wypukłość
wynika wypukłość ![]() .
.
Następujące przykłady pokazują, że ![]() może nie zawierać pewnego otoczenia celu, czyli, że
nie jest spełniona nawet lokalna sterowalność.
może nie zawierać pewnego otoczenia celu, czyli, że
nie jest spełniona nawet lokalna sterowalność.
Przykład 2.1 ([19], str. 18)
Niech ![]() ,
, ![]() ,
,
| (2.11) |
Zatem
Rozwiązanie spełniające ![]() ma postać
ma postać
![\begin{array}[]{lll}x^{1}(t)&=&x^{1}_{0}\\
x^{2}(t)&=&x^{2}_{0}+\int\limits _{0}^{t}u(s)\,\mathrm{d}s\end{array}\,.](wyklady/tst/mi/mi149.png) |
(2.12) |
Stąd
![{\mathcal{C}}=\Bigg\{\left[\begin{array}[]{c}x^{1}\\
x^{2}\end{array}\right]\,:\quad x^{1}=0\,,\quad x^{2}\in\mathbb{R}^{1}\Bigg\}\,,](wyklady/tst/mi/mi406.png) |
czyli ![]() jest osią
jest osią ![]() .
.
Przykład 2.2 ([31], str. 30; [24], str. 34)
Niech ![]() ,
, ![]() ,
,
| (2.13) |
Zatem
Rozwiązanie spełniające ![]() ma postać
ma postać
![\left[\begin{array}[]{c}x^{1}(t)\\
x^{2}(t)\end{array}\right]=e^{t}\left[\begin{array}[]{c}x_{0}^{1}\\
x_{0}^{2}\end{array}\right]+\Big(e^{t}\int\limits _{0}^{t}e^{{-s}}u(s)\,{\mathrm{d}}s\Big)\left[\begin{array}[]{c}1\\
1\end{array}\right]\,.](wyklady/tst/mi/mi70.png) |
(2.14) |
Jeżeli ![]() , to
, to
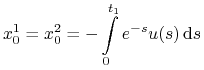 |
oraz
bo ![]() .
.
Stąd
![{\mathcal{C}}=\Bigg\{\left[\begin{array}[]{c}x^{1}\\
x^{2}\end{array}\right]\,:\quad x^{1}=x^{2}\,,\quad|x^{1}|<1\,,\quad|x^{2}|<1\Bigg\}\,.](wyklady/tst/mi/mi408.png) |
Przykłady 2.1 i 2.2 pokazują, że potrzebne są pewne warunki na macierze
![]() i
i ![]() . Warunki te zostaną wyrażone przez macierz sterowalności.
. Warunki te zostaną wyrażone przez macierz sterowalności.
Definicja 2.8
Dla (LA) wprowadzamy macierz sterowalności (controllability matrix):
![M=\underbrace{\Big[\, B,AB,A^{2}B,\ldots,A^{{n-1}}B\,\Big]}_{{\mathrm{macierz}\; n\times nm}}](wyklady/tst/mi/mi114.png) |
W dowodzie odpowiedniego twierdzenia (tw. 2.4) korzysta się z pojęcia hiperpłaszczyzny:
Definicja 2.9
![]() –wymiarową hiperpłaszczyzną (hyperplane) w
–wymiarową hiperpłaszczyzną (hyperplane) w ![]() nazywamy zbiór
nazywamy zbiór
gdzie ![]() ,
, ![]() oraz
oraz ![]() są zadane,
są zadane, ![]() oznacza
iloczyn skalarny wektorów
oznacza
iloczyn skalarny wektorów ![]() i
i ![]() .
.
Istotną rolę odgrywa tu wniosek z twierdzenia Mazura (geometrycznej wersji twierdzenia Hahna-Banacha) - twierdzenie o hiperpłaszczyźnie podpierającej — por. [30], str. 190.
Twierdzenie 2.3 (Twierdzenie o hiperpłaszczyźnie podpierającej)
Jeżeli ![]() , gdzie
, gdzie ![]() jest wypukłym zbiorem,
t.ż.
jest wypukłym zbiorem,
t.ż. ![]() , to istnieje
hiperpłaszczyzna podpierająca
, to istnieje
hiperpłaszczyzna podpierająca ![]() w
w ![]() (supporting hyperplane
(supporting hyperplane
![]() through
through ![]() ), tzn.
), tzn. ![]() leży po jednej
stronie
leży po jednej
stronie ![]() :
:
| (2.15) |
dla pewnego ![]() .
.
![]()
Twierdzenie 2.4
Dla (LA): Następujące trzy warunki są równoważne
-
(a)
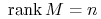
-
(b)
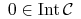 (lokalna sterowalność)
(lokalna sterowalność) -
(c)
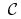 — otwarty w
— otwarty w 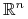
Dowód: [19], str. 18, [31], str. 31, [24], str. 35, [27], str. 108
![]()
Zauważmy, że równoważność ![]()
![]()
![]() wynika z
twierdzenia 2.1.
wynika z
twierdzenia 2.1.
1. Dowód ![]()
![]()
![]() , czyli
, czyli ![]()
![]()
![]() . Załóżmy więc
. Załóżmy więc ![]() , czyli
, czyli ![]() .
.
Wówczas istnieje wektor ![]() ,
, ![]() , prostopadły do każdej
kolumny macierzy
, prostopadły do każdej
kolumny macierzy ![]() , czyli
, czyli
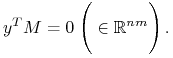 |
Stąd
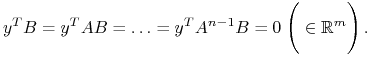 |
Niech ![]() będzie wielomianem charakterystycznym macierzy
będzie wielomianem charakterystycznym macierzy ![]()
gdzie ![]() jest macierzą jednostkową
jest macierzą jednostkową ![]() .
.
Mamy (twierdzenie Cayleya–Hamiltona)
Stąd
a zatem
Podobnie
i
Powtarzając to postępowanie
Stąd
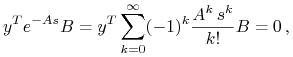 |
dla każdego ![]() .
.
Mamy (2.10). Stąd
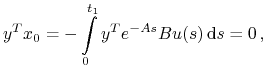 |
czyli istnieje niezerowy wektor ![]() , który jest prostopadły do każdego
, który jest prostopadły do każdego
![]() . Stąd wynika, że
. Stąd wynika, że ![]() leży w hiperpłaszczyźnie
prostopadłej do
leży w hiperpłaszczyźnie
prostopadłej do ![]() dla każdego
dla każdego ![]() . Zatem
. Zatem ![]() leży w hiperpłaszczyźnie prostopadłej do
leży w hiperpłaszczyźnie prostopadłej do ![]() i
i
Otrzymujemy więc, że ![]() , czyli
, czyli ![]() .
.
2. Dowód ![]()
![]()
![]() , czyli
, czyli ![]()
![]()
![]() . Załóżmy więc
. Załóżmy więc ![]() , czyli
, czyli ![]() .
Stąd dla każdego
.
Stąd dla każdego ![]() :
: ![]() , gdyż
, gdyż
![]() (nie istnieje kula
(nie istnieje kula ![]()
![]() nie istnieje kula
nie istnieje kula ![]() dla każdego
dla każdego ![]() ).
).
Ale ![]() oraz
oraz ![]() jest zbiorem wypukłym dla każdego
jest zbiorem wypukłym dla każdego
![]() (por. dowód twierdzenia 2.2).
Zatem istnieje hiperpłaszczyzna przechodząca przez
(por. dowód twierdzenia 2.2).
Zatem istnieje hiperpłaszczyzna przechodząca przez ![]() , taka że
, taka że ![]() leży po jednej stronie tej hiperpłaszczyzny (twierdzenie 2.3), tzn. istnieje
wektor
leży po jednej stronie tej hiperpłaszczyzny (twierdzenie 2.3), tzn. istnieje
wektor ![]() ,
, ![]() , taki że
, taki że
Stąd
![-b^{T}x_{0}=\int\limits _{0}^{{t_{1}}}b^{T}e^{{-As}}Bu(s)\,\mathrm{d}s\geq 0\qquad\forall\; u\in\mathbb{U}_{m}[0,t_{1}]\,.](wyklady/tst/mi/mi237.png) |
Z lematu 2.2 poniżej wynika, że
Wstawiając ![]() otrzymujemy
otrzymujemy ![]() . Następnie różniczkując względem
. Następnie różniczkując względem ![]() i
wstawiając
i
wstawiając ![]() otrzymujemy
otrzymujemy
Zatem niezerowy wektor ![]() jest prostopadły do każdej kolumny
jest prostopadły do każdej kolumny ![]() i
i
![]() , czyli
, czyli ![]() .
.
Lemat 2.2 (Nierówność całkowa)
Jeżeli
![\int\limits _{0}^{{t_{1}}}b^{T}e^{{-As}}Bu(s)\,\mathrm{d}s\geq 0\qquad\forall\; u\in\mathbb{U}_{m}[0,t_{1}]\,,](wyklady/tst/mi/mi259.png) |
(2.16) |
to
Dowód: [31], str. 32; [19], str. 21
![]()
Jeżeli ![]() , to
, to ![]() . Zatem z (2.16)
wynika, że
. Zatem z (2.16)
wynika, że
![\int\limits _{0}^{{t_{1}}}b^{T}e^{{-As}}Bu(s)\,\mathrm{d}s=0\qquad\forall\; u\in\mathbb{U}_{m}[0,t_{1}]\,.](wyklady/tst/mi/mi158.png) |
Niech ![]() . Jeżeli
. Jeżeli ![]() , to istnieje
, to istnieje ![]() , t.ż.
, t.ż.
![]() . Istnieje wtedy przedział
. Istnieje wtedy przedział ![]() , t.ż.
, t.ż. ![]() oraz
oraz ![]() na
na ![]() . Określmy sterowanie
. Określmy sterowanie
![u(t)=\left\{\begin{array}[]{ccc}\frac{v(t)}{|v(t)|}&\textrm{dla}&t\in\mathbb{I}\\
0&\textrm{dla}&t\in[0,t_{1}]\setminus\mathbb{I}\end{array}\right.\,.](wyklady/tst/mi/mi88.png) |
Wówczas mamy
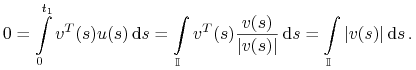 |
Otrzymujemy więc sprzeczność z założeniem ![]() .
.
Wniosek 2.1
Twierdzenie 2.4 można powtórzyć dla klas ![]() ,
, ![]() , gdyż dla tych klas
,,przechodzi” lemat 2.2.
, gdyż dla tych klas
,,przechodzi” lemat 2.2.
W dowodzie twierdzenia 2.4 pokazaliśmy, że
Wniosek 2.2
![]()
![]() istnieje hiperpłaszczyzna w
istnieje hiperpłaszczyzna w ![]() , t.ż.
, t.ż.
![]() leży w tej hiperpłaszczyźnie
leży w tej hiperpłaszczyźnie
![]()
![]() .
.
Ponadto
Wniosek 2.3
![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
| (2.17) |
jako funkcja zmiennej ![]() .
.
Definicja 2.10
Układ (LA) spełniający (2.17) nazywa się właściwy (proper).
(LA) jest właściwy wtedy i tylko wtedy, gdy
W rozpatrywanym tutaj przypadku ![]() warunek
warunek ![]() nie gwarantuje całkowitej
sterowalności
nie gwarantuje całkowitej
sterowalności ![]() , jak pokazuje prosty przykład
, jak pokazuje prosty przykład
Przykład 2.3 ([31], str. 33)
Niech ![]() . Rozważmy
. Rozważmy
Jeżeli ![]() (lub
(lub ![]() ), to odpowiedź na dowolne sterowanie rośnie
(maleje) wraz z
), to odpowiedź na dowolne sterowanie rośnie
(maleje) wraz z ![]() , a więc żadne sterowanie nie jest pomyślne. Mamy
, a więc żadne sterowanie nie jest pomyślne. Mamy ![]() , choć
, choć ![]() .
.
Jednakże przy dodatkowym warunku otrzymujemy:
Twierdzenie 2.5
Dla (LA) następujące dwa warunki są równoważne:
-
(a)
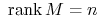 oraz
oraz 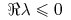 dla każdej wartości własnej
dla każdej wartości własnej 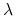 macierzy
macierzy
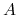
-
(b)
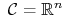 .
.
Dowód: [31], str. 34; [24], str. 37–38;
oraz 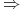 : [27], str. 112, [19], str. 22
: [27], str. 112, [19], str. 22
![]()
1. Dowód ![]()
![]()
![]() . Załóżmy, że
. Załóżmy, że ![]() oraz
oraz ![]() dla każdej
wartości własnej
dla każdej
wartości własnej ![]() macierzy
macierzy ![]() . Gdyby istniał
. Gdyby istniał ![]() , t.ż.
, t.ż. ![]() , to z
wypukłości
, to z
wypukłości ![]() (twierdzenie 2.2) oraz twierdzenia 2.3 wynikałoby, że
(twierdzenie 2.2) oraz twierdzenia 2.3 wynikałoby, że ![]() mógłby być
odseparowany od
mógłby być
odseparowany od ![]() hiperpłaszczyzną, tzn. istniałby
hiperpłaszczyzną, tzn. istniałby ![]() ,
, ![]() , t.ż.
, t.ż.
| (2.18) |
dla pewnego ![]() .
.
Pokażemy, że dla każdego ![]() oraz każdego
oraz każdego ![]() ,
, ![]() istnieje
istnieje ![]() oraz
oraz ![]() , t.ż.
, t.ż.
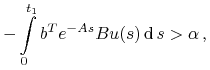 |
(2.19) |
co oznacza sprzeczność z (2.18), a zatem sprzeczność
z założeniem istnienia ![]() , t.ż.
, t.ż. ![]() , a więc
dowodzi prawdziwości
, a więc
dowodzi prawdziwości ![]()
![]()
![]() .
.
Niech
Z założenia, że ![]() oraz uwagi 2.3 wynika, że (LA) jest właściwy,
czyli
oraz uwagi 2.3 wynika, że (LA) jest właściwy,
czyli
| (2.20) |
Określmy sterowanie
![u(t)=\left\{\begin{array}[]{ccc}-\frac{v(t)}{|v(t)|}&\textrm{dla}&v(t)\not=0\\
0&\textrm{dla}&v(t)=0\,.\end{array}\right.](wyklady/tst/mi/mi252.png) |
Wówczas mamy
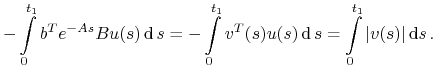 |
Pokażemy, że
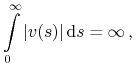 |
(2.21) |
a zatem istnienie takiego ![]() , że (2.19) jest spełniona.
, że (2.19) jest spełniona.
Załóżmy, że (2.21) nie jest spełniona, czyli
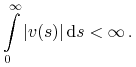 |
Wówczas ![]() spełnia
spełnia
| (2.22) |
Jeżeli ![]() jest wielomianem charakterystycznym macierzy
jest wielomianem charakterystycznym macierzy ![]() , to
, to
![]() . Stąd
. Stąd
Zatem funkcja ![]() spełnia liniowy układ równań różniczkowych ze stałymi
współczynnikami
spełnia liniowy układ równań różniczkowych ze stałymi
współczynnikami
Rozwiązaniem tego równania jest pewna liniowa kombinacja wyrazów postaci
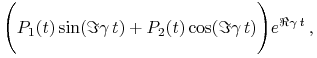 |
gdzie ![]() jest pierwiastkiem równania
jest pierwiastkiem równania
Zatem ![]() , lub
, lub ![]() , gdzie
, gdzie ![]() jest wartością własną macierzy
jest wartością własną macierzy ![]() .
Z założenia wynika, że
.
Z założenia wynika, że
co jest sprzeczne z (2.22). To kończy dowód implikacji ![]()
![]()
![]() .
.
2. Dowód ![]()
![]()
![]() . Pokażemy, że
. Pokażemy, że
-
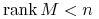 ,
,
lub
-
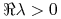 dla pewnej wartości własnej
dla pewnej wartości własnej 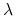 macierzy
macierzy 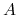
implikuje ![]() .
.
Jeżeli ![]() , to z wniosku 2.2 wynika, że
, to z wniosku 2.2 wynika, że
![]() .
.
Niech ![]() , dla pewnej wartości własnej
, dla pewnej wartości własnej ![]() macierzy
macierzy ![]() .
Jeżeli
.
Jeżeli ![]() jest (lewym) wektorem własnym (eigenvector), to
jest (lewym) wektorem własnym (eigenvector), to
Stąd
a zatem
Mamy
Wówczas
| (2.23) |
Mamy
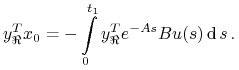 |
(2.24) |
Z (2.23) wynika, że prawa strona (2.24) jest ograniczona
jednostajnie względem ![]() . Zatem
. Zatem
dla pewnego ![]() . Czyli
. Czyli ![]() leży po jednej stronie pewnej
hiperpłaszczyzny, a więc
leży po jednej stronie pewnej
hiperpłaszczyzny, a więc ![]() .
To kończy dowód
.
To kończy dowód ![]()
![]()
![]() .
.
Ćwiczenie 2.1
Czy twierdzenie 2.5 jest prawdziwe dla klas ![]() ,
, ![]() ,
,
![]() oraz
oraz ![]() ? Dla
? Dla ![]() można zastosować zasadę bang–bang
— por. twierdzenie 5.1.
można zastosować zasadę bang–bang
— por. twierdzenie 5.1.
Wniosek 2.4
Jeżeli ![]() oraz
oraz ![]() , dla pewnej wartości własnej
, dla pewnej wartości własnej ![]() macierzy
macierzy ![]() , to
, to
![]() .
.
Przykład 2.4 (Wagon odrzutowy — patrz przykład 1.2)
Mamy
![]() i układ jest właściwy. Jedyną (podwójną) wartością własną
macierzy
i układ jest właściwy. Jedyną (podwójną) wartością własną
macierzy ![]() jest
jest ![]() . Z twierdzenia 2.5 wynika, że
. Z twierdzenia 2.5 wynika, że ![]() , czyli
każdy stan początkowy może być doprowadzony do celu
, czyli
każdy stan początkowy może być doprowadzony do celu ![]() .
.
W przeciwieństwie do przypadku klasy sterowań ![]() o wartościach w
o wartościach w ![]() , rozważanego
w twierdzeniu 2.5, w przypadku sterowań o wartościach w
, rozważanego
w twierdzeniu 2.5, w przypadku sterowań o wartościach w ![]() okazuje się, że warunek
okazuje się, że warunek ![]() jest równoważny całkowitej sterowalności.
W przypadku
jest równoważny całkowitej sterowalności.
W przypadku ![]() klasę sterowań definiujemy jako
klasę sterowań definiujemy jako
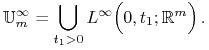 |
Dla uproszczenia notacji odpowiedni zbiór sterowalny bedziemy oznaczali jako ![]() ,
czyli tak samo, jak w przypadku
,
czyli tak samo, jak w przypadku ![]() (sens będzie wynikał z kontekstu).
(sens będzie wynikał z kontekstu).
Wówczas można sformułować następujące twierdzenie:
Twierdzenie 2.6
Dla (LA) i klasy sterowań ![]() następujące dwa warunki są
równoważne:
następujące dwa warunki są
równoważne:
-
(a)
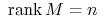 ,
, -
(b)
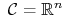 .
.
Dowód: por. [14], str. 58; [27], str. 107.
![]()
1. Dowód ![]()
![]()
![]() , czyli
, czyli ![]()
![]()
![]() jest identyczny jak punkt 1 dowodu twierdzenia 2.4.
jest identyczny jak punkt 1 dowodu twierdzenia 2.4.
2. Dowód ![]()
![]()
![]() . Załóżmy, że
. Załóżmy, że ![]() . Z
twierdzenia 2.4 wynika, że istnieje otwarta kula
. Z
twierdzenia 2.4 wynika, że istnieje otwarta kula ![]() o środku w
o środku w ![]() i promieniu
i promieniu ![]() , t.ż.
, t.ż. ![]() .
Dla dowolnego
.
Dla dowolnego ![]() istnieje stała
istnieje stała ![]() , t.ż.
, t.ż.
czyli istnieje ![]() oraz
oraz ![]() , t.ż.
, t.ż.
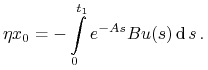 |
Stąd
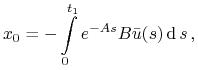 |
gdzie ![]() , co kończy dowód.
, co kończy dowód.
Okazuje się (por. [31], str. 37), że dla klasy sterowań ![]() ,,prawie wszystkie” układy (LA) są lokalnie sterowalne
(tzn. spełniają
,,prawie wszystkie” układy (LA) są lokalnie sterowalne
(tzn. spełniają ![]() ),
a dla klasy sterowań
),
a dla klasy sterowań ![]() ,,prawie wszystkie” układy (LA) są
całkowicie sterowalne (tzn. spełniają
,,prawie wszystkie” układy (LA) są
całkowicie sterowalne (tzn. spełniają ![]() ).
).
Odległość między dwoma układami (LA):
(![]() ) i (
) i (![]() ), czyli
), czyli ![]() i
i ![]() ,
odpowiednio, określamy jako
,
odpowiednio, określamy jako
gdzie ![]() i analogicznie
i analogicznie ![]() .
.
Zatem dwa układy są bliskie, jeżeli elementy odpowiednich macierzy są bliskie.
Twierdzenie 2.7
Zbiór wszystkich sterowalnych (LA) jest otwarty i gęsty w przestrzeni metrycznej wszystkich (LA), gdzie ,,sterowalność” rozumiemy w sensie
-
całkowitej sterowalności dla
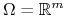 ,
, -
lokalnej sterowalności dla
![\Omega=[-1,1]^{m}](wyklady/tst/mi/mi277.png) .
.
Dowód: [31], str. 37.
![]()
Z twierdzenia 2.4, lub twierdzenia 2.6, w obu rozważanych przypadkach,
sterowalność jest równoważna warunkowi ![]() . Ten warunek oznacza, że istnieje
(
. Ten warunek oznacza, że istnieje
(![]() )–macierz
)–macierz ![]() , będąca podmacierzą
, będąca podmacierzą ![]() , t.ż.
, t.ż. ![]() .
.
Jeżeli układ (![]() ) jest bliski (
) jest bliski (![]() ), to odpowiednia
), to odpowiednia ![]() podmacierz
podmacierz
![]() macierzy
macierzy ![]() jest bliska odpowiedniej podmacierzy
jest bliska odpowiedniej podmacierzy ![]() macierzy
macierzy ![]() .
Jeżeli
.
Jeżeli ![]() , to
, to ![]() dla
dla ![]() —
małego. Zatem układy sterowalne są zbiorem otwartym.
—
małego. Zatem układy sterowalne są zbiorem otwartym.
Załóżmy, że ![]() nie jest sterowalny, tzn.
nie jest sterowalny, tzn. ![]() , gdzie
, gdzie
![]() . Chcemy pokazać istnienie układu (
. Chcemy pokazać istnienie układu (![]() )
— bliskiego układowi (
)
— bliskiego układowi (![]() ) — t.ż.
) — t.ż. ![]() , dla pewnej
, dla pewnej ![]() podmacierzy
podmacierzy ![]() macierzy
macierzy ![]() .
.
![]() może być traktowany jako wielomian
może być traktowany jako wielomian ![]() elementów macierzy
elementów macierzy ![]() i
i ![]() , gdzie
, gdzie ![]() .
Mamy
.
Mamy
dla ![]() – elementów macierzy
– elementów macierzy ![]() ,
, ![]() .
.
Wystarczy pokazać, że: dla niezerowego wielomianu ![]() , t.ż.
, t.ż.
![]() , istnieje
, istnieje ![]() — dowolnie bliskie
— dowolnie bliskie ![]() , t.ż.
, t.ż.
Powyższe zdanie wynika z faktu, że niezerowy wielomian ![]() zmiennych nie może znikać w żadnej
zmiennych nie może znikać w żadnej
![]() –wymiarowej kuli: gdyby znikał, to biorąc pochodne cząstkowe pokazalibyśmy, że wszystkie
współczynniki się zerują.
–wymiarowej kuli: gdyby znikał, to biorąc pochodne cząstkowe pokazalibyśmy, że wszystkie
współczynniki się zerują.




