4. Sterowalność dla układów nieliniowych
Rozważymy układ nieliniowy (NLA)
| (4.1) |
z celem ![]() . Zakładamy, że
. Zakładamy, że ![]() i
i ![]() jest klasy
jest klasy ![]() na
na
![]() .
.
Istotną rolę będzie pełniła linearyzacja (NLA) wokół ![]() :
:
| (4.2) |
gdzie
![A_{f}=\bigg[\frac{\partial f^{i}}{\partial x^{j}}(0,0)\bigg]_{{i,j=1,\ldots,n}}\,,\qquad B_{f}=\bigg[\frac{\partial f^{i}}{\partial u^{k}}(0,0)\bigg]_{{\genfrac{}{}{0pt}{}{i=1,\ldots,n}{k=1,\ldots,m}}}\,.](wyklady/tst/mi/mi490.png) |
Chcemy o sterowalności dla (NLA) w otoczeniu ![]() wnioskować ze
sterowalności linearyzacji wokół
wnioskować ze
sterowalności linearyzacji wokół ![]() .
.
Definicja 4.1
Dla (NLA) wprowadzamy macierz sterowalności układu zlinearyzowanego:
![M_{f}=\underbrace{\Big[\, B_{f},A_{f}B_{f},A_{f}^{2}B_{f},\ldots,A_{f}^{{n-1}}B_{f}\,\Big]}_{{\mathrm{macierz}\; n\times nm}}](wyklady/tst/mi/mi571.png) |
Twierdzenie 4.1
Dla (NLA): ![]()
![]()
![]() .
.
Dowód: [31], str. 38.![]()
Wniosek 4.1
Twierdzenie 4.1 zachodzi dla wszystkich sterowań, dla których można w danej klasie przedłużać sterowanie zerem.
Jednakże odpowiednik twierdzenia 4.1 dla ![]() jest fałszywy,
jak pokazuje następujący przykład:
jest fałszywy,
jak pokazuje następujący przykład:
Przykład 4.1 (([31], str. 45))
Niech ![]() i
i
dla ![]() . Mamy
. Mamy
Zatem ![]() i
i ![]() leży we wnętrzu
leży we wnętrzu ![]() z twierdzenia
4.1 (a także dla
z twierdzenia
4.1 (a także dla ![]() oraz
oraz ![]() ).
Ale
).
Ale ![]() implikuje, że
implikuje, że ![]() równa się
równa się ![]() , albo
, albo ![]() ,
a zatem
,
a zatem ![]() . Stąd
. Stąd ![]() , gdyż
żaden punkt
, gdyż
żaden punkt ![]() nie może być doprowadzony do
nie może być doprowadzony do ![]() .
.
Ten sam przykład pokazuje, że zasada bang–bang (rozdział 5.1) nie zachodzi dla (NLA).
Twierdzenie 4.2
Dla (NLA): Jeżeli układ z zerowym sterowaniem (![]() ) jest globalnie
asymptotycznie stabilny i
) jest globalnie
asymptotycznie stabilny i ![]() , to
, to
![]() .
.
Dowód: [31], str. 43.
![]()
Dla (NLA) twierdzenie 4.1 gwarantuje istnienie ![]() , t.ż. istnieje
kula
, t.ż. istnieje
kula ![]() . Globalna asymptotyczna stabilność rozwiązania dla
. Globalna asymptotyczna stabilność rozwiązania dla ![]() implikuje, że
implikuje, że
dla każdego ![]() .
Zatem każde rozwiązanie z
.
Zatem każde rozwiązanie z ![]() wchodzi do
wchodzi do ![]() w skończonym czasie.
Następnie korzystamy z
w skończonym czasie.
Następnie korzystamy z ![]() .
.
Twierdzenie 4.2 wskazuje na ścisły związek pomiędzy teorią stabilności a sterowalnością.
Ważnym pojęciem w badaniu stabilności jest funkcja Lapunova (por. [35], rozdział 7.2, [21], rozdział 26).
Definicja 4.2
Niech ![]() będzie otoczeniem punktu równowagi
będzie otoczeniem punktu równowagi ![]() układu
układu
![]() .
Funkcję
.
Funkcję ![]() nazywamy funkcją Lapunova, jeżeli
nazywamy funkcją Lapunova, jeżeli
-
jest ciągła w
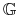 i różniczkowalna w
i różniczkowalna w 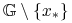 ,
, -
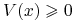
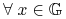 ,
, 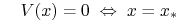
-
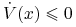
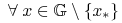 , gdzie
, gdzie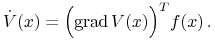
Definicja 4.3
Mocną funkcją Lapunova nazywamy ![]() , jeżeli
, jeżeli
-
jest funkcją Lapunova w
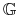 ,
,
-
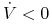
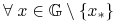 .
.
Twierdzenie 4.3
![]()
-
Jeżeli istnieje funkcja Lapunova, to punkt równowagi
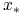 jest stabilny
w sensie Lapunova.
jest stabilny
w sensie Lapunova. -
Jeżeli istnieje mocna funkcja Lapunova, to punkt równowagi
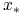 jest
asymptotycznie stabilny.
jest
asymptotycznie stabilny.
![]()
Przykład 4.2 (por. [31], str. 43)
Punkt materialny, o jednostkowej masie, poruszający się pod wpływem zewnętrznej siły
![]() można opisać zgodnie z II zasadą dynamiki Newtona:
można opisać zgodnie z II zasadą dynamiki Newtona:
Jeżeli punkt zawieszony jest na sprężynie i ruch odbywa się w ośrodku stawiającym opór, to można przyjąć, że
gdzie ![]() jest siłą oporu środowiska,
jest siłą oporu środowiska, ![]() ,
, ![]() jest siłą
sprężystości oraz
jest siłą
sprężystości oraz ![]() jest siłą wymuszającą (lub tłumiącą). Na przykład dla prawa Hooke'a
jest siłą wymuszającą (lub tłumiącą). Na przykład dla prawa Hooke'a
![]() — por. przykład 1.3.
— por. przykład 1.3.
Załóżmy, że ![]() i
i ![]() są funkcjami klasy
są funkcjami klasy ![]() ,
, ![]() .
.
Przyjmując ![]() ,
, ![]() otrzymujemy układ równań
otrzymujemy układ równań
| (4.3) |
Układ zlinearyzowany ma postać
| (4.4) |
Mamy
| (4.5) |
Zatem, dla każdego warunku gwarantującego globalną asymptotyczną stabilność rozwiązania
![]() układu dla
układu dla ![]() , otrzymamy
, otrzymamy ![]() .
.
Jeżeli
-
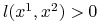 dla każdego
dla każdego 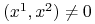 ,
, -
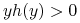 dla każdego
dla każdego 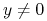 ,
, -
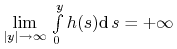 ,
,
to rozwiązanie ![]() jest globalnie asymptotycznie stabilne.
jest globalnie asymptotycznie stabilne.
Rzeczywiście, niech:
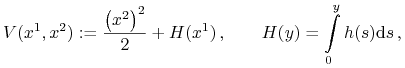 |
| (4.6) |
oraz wzdłuż rozwiązań układu z ![]() :
:
![\begin{array}[]{ll}\dot{V}(x^{1},x^{2})=x^{2}\dot{x}^{2}+h(x^{1})\dot{x}^{1}=&\\
x^{2}\Big(-l(x^{1},x^{2})x^{2}-h(x^{1})\Big)+h(x^{1})x^{2}=-\big(x^{2}\big)^{2}l(x^{1},x^{2})\leq&0\,.\end{array}](wyklady/tst/mi/mi517.png) |
(4.7) |
Zatem ![]() jest funkcją Lapunova i rozwiązanie
jest funkcją Lapunova i rozwiązanie ![]() dla
dla ![]() jest
stabilne (w sensie Lapunova). Argument ten nie wystarczy do pokazania asymptotycznej
stabilności, gdyż
jest
stabilne (w sensie Lapunova). Argument ten nie wystarczy do pokazania asymptotycznej
stabilności, gdyż ![]() zeruje się nie tylko dla
zeruje się nie tylko dla ![]() , ale
również dla punktów
, ale
również dla punktów ![]() , takich że
, takich że ![]() ,
, ![]() . Aby pokazać asymptotyczną
stabilność wystarczy wykazać, że jeżeli trajektoria przechodzi przez taki punkt
. Aby pokazać asymptotyczną
stabilność wystarczy wykazać, że jeżeli trajektoria przechodzi przez taki punkt ![]() ,
,
![]() , to jest to punkt przegięcia (flex point) funkcji
, to jest to punkt przegięcia (flex point) funkcji
![]() i funkcja ta jest ściśle malejąca (por. [35], str. 211, przykład 7.4).
Jeżeli
i funkcja ta jest ściśle malejąca (por. [35], str. 211, przykład 7.4).
Jeżeli ![]() jest t.ż.
jest t.ż. ![]() i
i ![]() ,
to
,
to ![]() . Stąd
. Stąd ![]() ma ten sam znak
i
ma ten sam znak
i ![]() w sąsiedztwie
w sąsiedztwie ![]() . Zatem
. Zatem ![]() ma w
ma w ![]() punkt przegięcia i jest ściśle malejąca. To gwarantuje asymptotyczną stabilność.
punkt przegięcia i jest ściśle malejąca. To gwarantuje asymptotyczną stabilność.
Globalność wynika z warunku 4.6 — por. [23], twierdzenia 26.2, 26.3, str. 108–109.
Istnieje związek pomiędzy ![]() i
i ![]() :
:
Twierdzenie 4.4
Dla (NLA): jeżeli ![]() , to
, to
![]() .
.
Dowód: [31], str. 46–47.![]()




