5. Zasada bang–bang
Twierdzenie 5.1 (Zasada bang–bang (bang–bang principle))
Dla (LA):
Niech ![]() oraz
oraz ![]() . Wówczas istnieje sterowanie bang-bang
. Wówczas istnieje sterowanie bang-bang ![]() ,
które prowadzi
,
które prowadzi ![]() do
do ![]() w czasie
w czasie ![]() .
.
Zatem
| (5.1) |
Dowód: [19], str. 27–30, [27], str. 171.
![]()
Dowód zostanie przeprowadzony w 3 krokach.
-
Niech
![L^{{\infty}}(0,t)=\Big\{ u:\,]0,t[\,\to{\mathbb{R}}^{m}\;:\quad\| u\| _{{\infty}}:=\mathrm{ess}\sup\limits _{{0<s<t}}|u(s)|<\infty\Big\}](wyklady/tst/mi/mi652.png)
dla
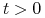 .
.Definicja 5.1
Niech
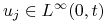 , dla
, dla 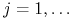 , oraz
, oraz 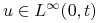 . Ciąg
. Ciąg
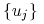 jest zbieżny do
jest zbieżny do 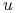 słabo
słabo (weakly
(weakly convergent)
w
convergent)
w 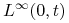 (zapis
(zapis 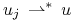 ), jeżeli
), jeżeli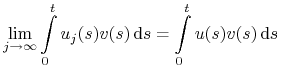
dla każdego
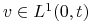 .
.Niech
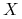 będzie przestrzenią Banacha. Mamy
będzie przestrzenią Banacha. Mamy=x^{{\ast}}(x)\quad\forall\; x^{{\ast}}\in X^{{\ast}}\,.](wyklady/tst/mi/mi667.png)
W
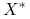 można zdefiniować następujące topologie (poprzez zdefiniowanie zbieżności ciągów)
można zdefiniować następujące topologie (poprzez zdefiniowanie zbieżności ciągów)-
topologię mocną:
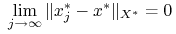 ,
, -
topologię słabą:
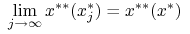 dla
każdego
dla
każdego 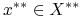 ,
, -
topologię słabą
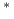 :
: 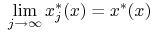 dla
każdego
dla
każdego 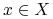 .
.
Słaba topologia w
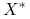 jest najsłabszą topologią, w której każdy
jest najsłabszą topologią, w której każdy 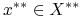 pozostaje ciągły.
pozostaje ciągły.Słaba
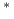 topologia w
topologia w 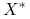 jest najsłabszą topologią, przy której funkcjonał
jest najsłabszą topologią, przy której funkcjonał ![J[x]](wyklady/tst/mi/mi598.png) ,
zdefiniowany na
,
zdefiniowany na 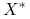 jest ciągły dla każdego
jest ciągły dla każdego 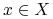 .
.Kula jednostkowa w
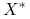 jest zwarta w słabej
jest zwarta w słabej topologii (twierdzenie
Banacha–Alaoglu–Bourbakiego).
topologii (twierdzenie
Banacha–Alaoglu–Bourbakiego).Mamy
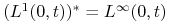 ,
, 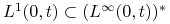 .
.Ćwiczenie 5.1
Pokazać, że
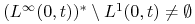 .
.Rozwiązanie ćwiczenia: Niech
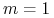 . Rozważmy ustalony przedział
. Rozważmy ustalony przedział ![[0,t]](wyklady/tst/mi/mi623.png) ,
, 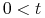 . Niech
. Niech 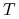 będzie przekształceniem
będzie przekształceniem
![C([0,t];\mathbb{R}^{1})\ni f\mapsto f(0)](wyklady/tst/mi/mi1558.png) .
Wówczas mamy
.
Wówczas mamy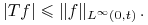
Z twierdzenia Hahna–Banacha (por. [34], §17) istnieje rozszerzenie tego funkcjonału liniowego (do
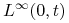 ) zachowujące normę (oznaczamy również przez
) zachowujące normę (oznaczamy również przez 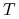 ):
):
Jeżeli
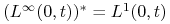 , to istnieje
, to istnieje 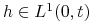 , t.ż.
, t.ż.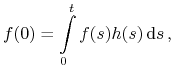
dla
![f\in C([0,t];\mathbb{R}^{1})](wyklady/tst/mi/mi1562.png) .
.
Stąd jeżeli
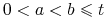 , to
, to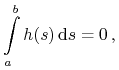
a zatem
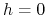 prawie wszędzie. Dla
prawie wszędzie. Dla 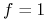 otrzymujemy sprzeczność:
otrzymujemy sprzeczność: 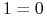 .
.Twierdzenie 5.2 (Alaoglu)
Niech
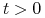 oraz
oraz
![\{ u_{j}\} _{{j=1,\ldots}}\subset{{\mathbb{U}}}_{m}[0,t]](wyklady/tst/mi/mi607.png) .
Wówczas istnieje podciąg
.
Wówczas istnieje podciąg 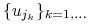 oraz
oraz
![u\in{{\mathbb{U}}}_{m}[0,t]](wyklady/tst/mi/mi582.png) , t.ż
, t.ż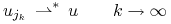
Definicja 5.2
Punkt
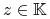 nazywa się ekstremalny
(extreme) jeżeli
nazywa się ekstremalny
(extreme) jeżeli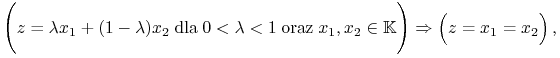
czyli nie istnieją punkty
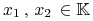 ,
, 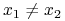 oraz
oraz 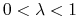 , t.ż.
, t.ż.
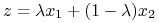 .
.Twierdzenie 5.3 (Kreina–Milmana)
Niech
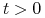 oraz
oraz 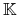 będzie niepustym, wypukłym podzbiorem
będzie niepustym, wypukłym podzbiorem 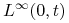 , zwartym w słabej
, zwartym w słabej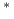 topologii. Wówczas
topologii. Wówczas 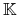 ma (przynajmniej jeden) punkt ekstremalny.
ma (przynajmniej jeden) punkt ekstremalny.Dowód: [34], str. 212.

-
-
Rozważamy zagadnienie (LA):
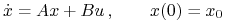
Niech
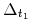 będzie zbiorem sterowań, które prowadzą
będzie zbiorem sterowań, które prowadzą
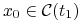 do
do 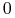 w czasie
w czasie 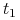 :
:![{\Delta _{{t_{1}}}}=\Big\{ u\in{{\mathbb{U}}}_{m}[0,{{t_{1}}}]\,:\quad u\;{\textrm{prowadzi}}\; x_{0}\;{\textrm{do}}\; 0\;{\textrm{w}}\;{{t_{1}}}\,\Big\}](wyklady/tst/mi/mi661.png)
Pokażemy, że
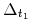 spełnia założenia tw. Kreina–Milmana,
a następnie, że punkt ekstremalny jest sterowaniem bang–bang.
spełnia założenia tw. Kreina–Milmana,
a następnie, że punkt ekstremalny jest sterowaniem bang–bang.Lemat 5.1
Zbiór
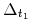 spełnia założenia tw. Kreina–Milmana.
spełnia założenia tw. Kreina–Milmana.Dowód: [19], str. 27–30, [27], str. 171.

 , więc
, więc  .
Pokażemy, ze
.
Pokażemy, ze 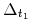 jest wypukły.
jest wypukły.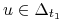 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy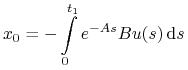
Niech
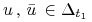 oraz
oraz 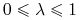 .
.Wówczas
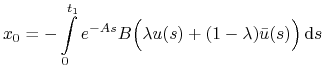
Zatem
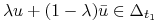 .
.Pokażemy zwartość w słabej
 topologii.
Niech
topologii.
Niech 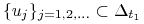 .
.Z tw. Alaoglu: ist.
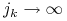 oraz
oraz ![u\in{{\mathbb{U}}}_{m}[0,{{t_{1}}}]](wyklady/tst/mi/mi606.png) ,
t.ż.
,
t.ż. 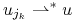 dla
dla 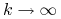
Musimy pokazać, że
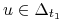 .
Z
.
Z 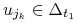 wynika, że
wynika, że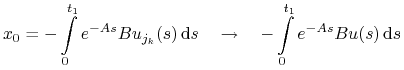
z definicji słabej
∎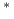 zbieżności. Zatem
zbieżności. Zatem 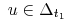 .
.Z twierdzenia Kreina–Milmana istnieje punkt ekstremalny
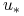 w
w 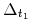 .
. -
Pokażemy, że dla prawie każdego
![t\in\,[0,{{t_{1}}}]\,](wyklady/tst/mi/mi599.png) i każdego
i każdego 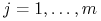 :
: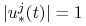
Załóżmy, że nie! Istnieje więc indeks
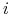 oraz podzbiór
oraz podzbiór
![{\mathbb{G}}\subset\,[0,{{t_{1}}}]\,](wyklady/tst/mi/mi670.png) o dodatniej mierze, t.ż.
o dodatniej mierze, t.ż. 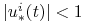 dla
dla 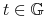 .
Istnieje
.
Istnieje 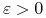 oraz
oraz 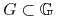 , t.ż.
, t.ż.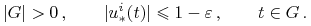
Niech
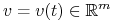 będzie t.ż.
będzie t.ż.
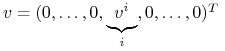 , gdzie
, gdzie-
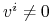 na
na 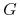 ,
, -
 ,
, -
![v\Big|_{{[0,{{t_{1}}}]\setminus G}}=0](wyklady/tst/mi/mi675.png)
oraz
-
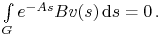
Niech

Mamy
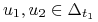 . Rzeczywiście
. Rzeczywiście![\begin{array}[]{ll}-&\int\limits _{0}^{{{{t_{1}}}}}e^{{-As}}Bu_{1}(s){\rm d}s=\\
=-&\int\limits _{0}^{{{{t_{1}}}}}e^{{-As}}Bu_{{\ast}}(s)\,{\mathrm{d}}s-\varepsilon\underbrace{\mathstrut{\int\limits _{0}^{{{{t_{1}}}}}e^{{-As}}Bv(s){\rm d}s}}_{{=0}}\,=\, x_{0}\end{array}](wyklady/tst/mi/mi636.png)
Mamy
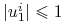 :
: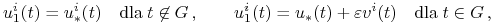
Na
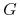 mamy
mamy 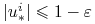 , a zatem
, a zatem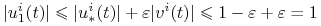
Podobnie
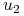 , zatem
, zatem 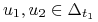 .
.
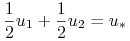
Sprzeczność: bo
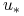 jest punktem ekstremalnym
jest punktem ekstremalnym
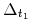 .
. -
Uwaga 5.1
Zasada bang–bang pozostaje bez zmiany w przypadku, gdy celem
jest ![]() ,
, ![]() .
Rzeczywiście:
.
Rzeczywiście:
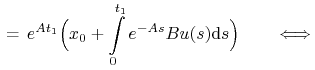 |
||||
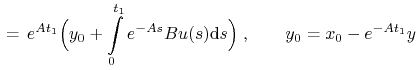 |
Z zasady bang–bang istnieje ![]() , t.ż.
, t.ż.
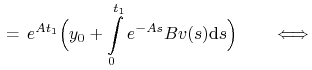 |
||||
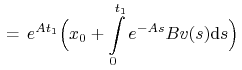 |
Uwaga 5.2
Analogicznie dla




