Zagadnienia
1. Procesy stochastyczne. Proces Wienera
Podczas pierwszego wykładu określimy czym jest proces stochastyczny oraz zdefiniujemy proces Wienera – najważniejszy przykład procesu o ciągłych trajektoriach.
1.1. Podstawowe definicje
Zaczniemy od podania ważnych definicji używanych podczas całego wykładu.
Definicja 1.1
Niech ![]() będzie przestrzenią probabilistyczną,
będzie przestrzenią probabilistyczną, ![]() przestrzenią
mierzalną, zaś
przestrzenią
mierzalną, zaś ![]() dowolnym zbiorem.
Procesem stochastycznym o wartościach w
dowolnym zbiorem.
Procesem stochastycznym o wartościach w ![]() , określonym na zbiorze
, określonym na zbiorze ![]() , nazywamy
rodzinę zmiennych losowych
, nazywamy
rodzinę zmiennych losowych ![]() , przyjmujących wartości w
zbiorze
, przyjmujących wartości w
zbiorze ![]() .
.
Uwaga 1.1
W czasie wszystkich dalszych wykładów ![]() będzie podzbiorem
będzie podzbiorem ![]() (najczęściej
przedziałem, niekoniecznie ograniczonym), zaś
(najczęściej
przedziałem, niekoniecznie ograniczonym), zaś ![]() lub
lub ![]() .
Parametr
.
Parametr ![]() można wówczas interpretować jako czas.
można wówczas interpretować jako czas.
Definicja 1.2
Trajektorią procesu![]() nazywamy funkcję (losową!)
nazywamy funkcję (losową!)
![]() , określoną na zbiorze
, określoną na zbiorze ![]() o wartościach w
o wartościach w ![]() .
.
Definicja 1.3
Powiemy, że proces ![]() ,
, ![]() ma przyrosty niezależne
jeśli dla dowolnych indeksów
ma przyrosty niezależne
jeśli dla dowolnych indeksów ![]() ze zbioru
ze zbioru ![]() ,
zmienne losowe
,
zmienne losowe ![]() są niezależne.
są niezależne.
Definicja 1.4
Mówimy, że proces stochastyczny ![]() ma przyrosty stacjonarne, jeśli
rozkład
ma przyrosty stacjonarne, jeśli
rozkład ![]() zależy tylko od
zależy tylko od ![]() , czyli
, czyli
1.2. Proces Wienera (ruch Browna)
Definicja 1.5
Procesem Wienera (ruchem Browna) nazywamy proces
stochastyczny ![]() taki, że
taki, że
| Trajektorie |
Uwaga 1.2
Warunek (W3) oznacza, że istnieje zbiór ![]() taki, że
taki, że ![]() oraz dla wszystkich
oraz dla wszystkich ![]() ,
,
![]() jest funkcją ciągłą na
jest funkcją ciągłą na ![]() . Czasami
w definicji procesu Wienera zakłada się, że wszystkie trajektorie są
ciągłe oraz
. Czasami
w definicji procesu Wienera zakłada się, że wszystkie trajektorie są
ciągłe oraz ![]() .
.
1.3. Charakteryzacje procesu Wienera
Najpierw podamy twierdzenie, które znacznie ułatwia sprawdzanie, że dany proces jest procesem Wienera. Musimy wpierw podać ważną definicję.
Definicja 1.6
Proces ![]() nazywamy gaussowskim, jeśli wszystkie
skończenie wymiarowe rozkłady
nazywamy gaussowskim, jeśli wszystkie
skończenie wymiarowe rozkłady ![]() są gaussowskie, tzn. wektor
są gaussowskie, tzn. wektor
![]() ma rozkład gaussowski
dla dowolnych
ma rozkład gaussowski
dla dowolnych ![]() .
.
Przykład 1.1
Następujące procesy są procesami gaussowskimi:
-
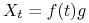 , gdzie
, gdzie 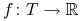 dowolne oraz
dowolne oraz 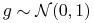 ,
, -
proces Wienera
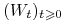 ,
, -
most Browna
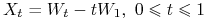 .
.
Przykład 1.2
Procesy ![]() ,
, ![]() nie są gaussowskie.
nie są gaussowskie.
Twierdzenie 1.1
Proces ![]() jest procesem Wienera wtedy i tylko wtedy, gdy jest
procesem gaussowskim, o ciągłych trajektoriach p.n. takim, że
jest procesem Wienera wtedy i tylko wtedy, gdy jest
procesem gaussowskim, o ciągłych trajektoriach p.n. takim, że ![]() oraz
oraz
![]() .
.
![]() : Mamy
: Mamy ![]() oraz
oraz ![]() na mocy (W0) i (W2). Ponadto z niezależności przyrostów, dla
na mocy (W0) i (W2). Ponadto z niezależności przyrostów, dla ![]() ,
,
![]() .
.
![]() : Zauważmy, że
: Zauważmy, że ![]() , więc spełniony jest warunek (W0). Dla
, więc spełniony jest warunek (W0). Dla ![]() ,
zmienna
,
zmienna ![]() ma rozkład normalny ze średnią
ma rozkład normalny ze średnią ![]() i wariancją
i wariancją
![]() , więc zachodzi (W2). By
sprawdzić niezależność przyrostów ustalmy
, więc zachodzi (W2). By
sprawdzić niezależność przyrostów ustalmy ![]() . Zauważmy, że
wektor
. Zauważmy, że
wektor ![]() ma rozkład gaussowski, więc jego współrzędne są niezależne wtedy i tylko
wtedy, gdy są nieskorelowane. Mamy jednak dla
ma rozkład gaussowski, więc jego współrzędne są niezależne wtedy i tylko
wtedy, gdy są nieskorelowane. Mamy jednak dla ![]() ,
,
oraz
Kolejne twierdzenie pokazuje, że (z dokładnością do drobnych technicznych założeń oraz normalizacji) proces Wienera jest jedynym procesem o ciągłych trajektoriach oraz niezależnych i stacjonarnych przyrostach.
Twierdzenie 1.2
Załóżmy, że proces ![]() spełnia warunki (W0), (W1), (W3)
(z
spełnia warunki (W0), (W1), (W3)
(z ![]() zastąpionym przez
zastąpionym przez ![]() ) oraz
) oraz
Wówczas ![]() jest procesem Wienera.
jest procesem Wienera.
Określmy dla ![]() ,
, ![]() oraz
oraz ![]() . Zauważmy, że
na mocy niezależności i stacjonarności przyrostów,
. Zauważmy, że
na mocy niezależności i stacjonarności przyrostów,
Ponadto oczywiście ![]() , zatem funkcja
, zatem funkcja ![]() jest addytywna i niemalejąca na
jest addytywna i niemalejąca na
![]() , więc
, więc ![]() dla pewnego
dla pewnego ![]() , co wobec (W2b) daje
, co wobec (W2b) daje ![]() .
Analogicznie sprawdzamy, że
.
Analogicznie sprawdzamy, że ![]() , wiemy też, że
, wiemy też, że ![]() , stąd wnioskujemy, że
, stąd wnioskujemy, że
![]() dla
dla ![]() wymiernych. Weźmy
wymiernych. Weźmy ![]() i wybierzmy dążący do
i wybierzmy dążący do ![]() ciąg liczb wymiernych
ciąg liczb wymiernych
![]() .
Na mocy (W2c),
.
Na mocy (W2c), ![]() , wiemy też, że
, wiemy też, że ![]() , zatem
, zatem
![]() dla pewnej stałej
dla pewnej stałej ![]() . Z ciągłości trajektorii
. Z ciągłości trajektorii ![]() prawie na pewno, czyli również według prawdopodobieństwa. Zatem dla
prawie na pewno, czyli również według prawdopodobieństwa. Zatem dla ![]() ,
,
dla dostatecznie dużych ![]() . Stąd
. Stąd ![]() . Wykazaliśmy więc, że
. Wykazaliśmy więc, że
![]() ma średnią zero i wariancję
ma średnią zero i wariancję ![]() .
.
Ustalmy ![]() , chcemy pokazać, że
, chcemy pokazać, że ![]() ma rozkład normalny
ma rozkład normalny ![]() . Zauważmy, że
. Zauważmy, że
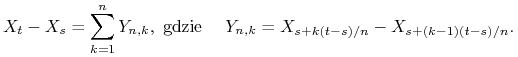 |
Zmienne ![]() tworzą układ trójkątny, możemy więc skorzystać
z Centralnego Twierdzenia Granicznego i wykazać, że
tworzą układ trójkątny, możemy więc skorzystać
z Centralnego Twierdzenia Granicznego i wykazać, że ![]() zbiega
do
zbiega
do ![]() według rozkładu. Mamy
według rozkładu. Mamy
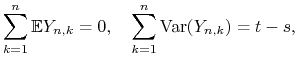 |
wystarczy więc sprawdzić warunek Lindeberga. Dla ![]() ,
,
![\displaystyle=\sum _{{k=1}}^{n}{\mathbb{E}}|Y_{{n,k}}|^{2}{\mathrm{I}}_{{\{|Y_{{n,k}}|\geq\varepsilon\}}}\leq{\mathbb{E}}\Big[\Big(\sum _{{k=1}}^{n}|Y_{{n,k}}|^{2}\Big){\mathrm{I}}_{{\{\max _{{k\leq n}}|Y_{{n,k}}|\geq\varepsilon\}}}\Big]](wyklady/was/mi/mi66.png) |
|||
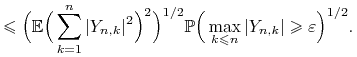 |
Zauważmy, że zmienne ![]() dla ustalonego
dla ustalonego ![]() są niezależne i mają średnią zero, zatem
są niezależne i mają średnią zero, zatem
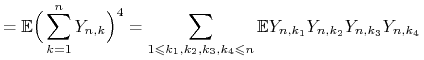 |
|||
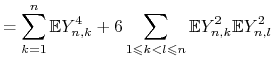 |
|||
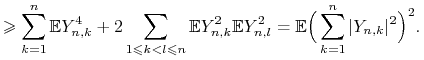 |
Z ciągłości trajektorii ![]() wynika, że
wynika, że ![]() przy
przy ![]() , zatem spełniony jest warunek Lindeberga
, zatem spełniony jest warunek Lindeberga ![]() .
.
Uwaga 1.3
Warunek (W2c) nie jest konieczny - zob. Twierdzenie 5 z paragrafu 13.1 książki [3].
Okazuje się, że również nie trzeba zakładać skończoności wariancji ani nawet istnienia
wartości średniej ![]() - warunek (W2b) ma charakter czysto normalizacyjny.
Dokładniej zachodzi następujące twierdzenie.
- warunek (W2b) ma charakter czysto normalizacyjny.
Dokładniej zachodzi następujące twierdzenie.
Twierdzenie 1.3
Załóżmy, że proces stochastyczny ![]() spełnia warunki
(W0),(W1), (W2a) i (W3). Wówczas istnieją stałe
spełnia warunki
(W0),(W1), (W2a) i (W3). Wówczas istnieją stałe ![]() i proces Wienera
i proces Wienera
![]() takie, że
takie, że
![]() dla wszystkich
dla wszystkich ![]() .
.
1.4. Uwagi i uzupełnienia
1.4.1. Konstrukcja Procesu Wienera
Podczas następnych wykładów podamy dość abstrakcyjną konstrukcję procesu Wienera opartą o ogólniejsze twierdzenia dotyczące istnienia i ciągłości trajektorii procesów stochastycznych. Alternatywna, bardziej bezpośrednia konstrukcja (wymagająca pewnej znajomości analizy funkcjonalnej) procesu Wienera jest zawarta w Ćwiczeniach 1.10-1.12.
1.4.2. Nieróżniczkowalność trajektorii
Trajektorie procesu Wienera mają wiele ciekawych własności, jedną z nich jest to, że prawdopodobieństwem 1 są funkcjami ciągłymi, nieróżniczkowalnymi w żadnym punkcie.
Twierdzenie 1.4
Prawie wszystkie trajektorie procesu Wienera ![]() są funkcjami
nieróżniczkowalnymi w żadnym punkcie, tzn.
są funkcjami
nieróżniczkowalnymi w żadnym punkcie, tzn.
1.5. Zadania
Ćwiczenie 1.1
Znajdź rozkład zmiennej ![]() .
.
Ćwiczenie 1.2
Dla jakich parametrów ![]() i
i ![]() , zmienne
, zmienne ![]() oraz
oraz ![]() są
niezależne?
są
niezależne?
Ćwiczenie 1.3
Udowodnij, że ![]() p.n.
p.n.
Ćwiczenie 1.4
Znajdź rozkład wektora losowego ![]() dla
dla ![]() .
.
Ćwiczenie 1.5
Udowodnij, że z prawdopodobieństwem ![]() trajektorie procesu Wienera są nieograniczone.
trajektorie procesu Wienera są nieograniczone.
Ćwiczenie 1.6
Udowodnij, że z
prawdopodobieństwem ![]() trajektorie
procesu Wienera nie są jednostajnie ciągłe na
trajektorie
procesu Wienera nie są jednostajnie ciągłe na ![]() .
.
Ćwiczenie 1.7
Udowodnij, że następujące procesy też są procesami Wienera:
i) ![]() (odbicie);
(odbicie);
ii) ![]() (przeskalowanie czasu);
(przeskalowanie czasu);
iii) ![]() dla
dla ![]() oraz
oraz ![]() (inwersja czasu);
(inwersja czasu);
iv) ![]() ;
;
v) ![]() dla
dla ![]() ,
, ![]() dla
dla ![]() , gdzie
, gdzie
![]() .
.
Ćwiczenie 1.8
Niech ![]() , gdzie
, gdzie
![]() będzie ciągiem
podziałów odcinka
będzie ciągiem
podziałów odcinka ![]() oraz
oraz
![]() oznacza średnicę
oznacza średnicę
![]() . Udowodnij, że
. Udowodnij, że
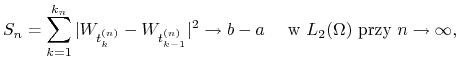 |
jeśli ![]() oraz
oraz ![]() p.n., jeśli
p.n., jeśli ![]() .
.
Ćwiczenie 1.9
Udowodnij, że prawie wszystkie trajektorie procesu Wienera mają nieskończone wahanie na każdym przedziale.
Ćwiczenie 1.10
Niech ![]() będzie dowolną bazą
będzie dowolną bazą ![]() ,
,
![]() oraz niech
oraz niech ![]() będzie ciągiem niezależnych zmiennych
będzie ciągiem niezależnych zmiennych
![]() . Wykaż, że szereg
. Wykaż, że szereg
![]() jest zbieżny w
jest zbieżny w ![]() dla dowolnego
dla dowolnego ![]() oraz
oraz
![]() ma te same rozkłady skończenie wymiarowe co proces Wienera.
ma te same rozkłady skończenie wymiarowe co proces Wienera.
Ćwiczenie 1.11
Niech ![]() . Układem Haara
nazywamy rodzinę funkcji
. Układem Haara
nazywamy rodzinę funkcji ![]() określonych na
określonych na ![]() wzorami
wzorami ![]() oraz dla
oraz dla ![]() ,
,
![h_{{n,k}}(t)=\left\{\begin{array}[]{ll}2^{{\frac{n-1}{2}}}&(2k-2)2^{{-n}}\leq t<(2k-1)2^{{-n}},\\
-2^{{\frac{n-1}{2}}}&(2k-1)2^{{-n}}\leq t<2k2^{{-n}},\\
0&\mbox{w pozostałych przypadkach.}\end{array}\right.](wyklady/was/mi/mi143.png) |
Układem Schaudera nazywamy rodzinę
funkcji ![]() określonych na
określonych na ![]() wzorem
wzorem ![]() .
Niech
.
Niech ![]() będzie rodziną niezależnych zmiennych losowych
o rozkładzie
będzie rodziną niezależnych zmiennych losowych
o rozkładzie ![]() , połóżmy
, połóżmy
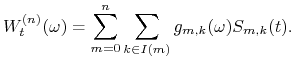 |
Wykaż, że dla prawie wszystkich ![]() ciąg funkcji
ciąg funkcji ![]() zbiega jednostajnie
na
zbiega jednostajnie
na ![]() do pewnej funkcji ciągłej
do pewnej funkcji ciągłej ![]() . Jeśli określimy np.
. Jeśli określimy np. ![]() dla pozostałych
dla pozostałych ![]() to tak zdefiniowany proces stochastyczny jest procesem Wienera
na
to tak zdefiniowany proces stochastyczny jest procesem Wienera
na ![]() .
.
Ćwiczenie 1.12
Niech ![]() będzie procesem Wienera na
będzie procesem Wienera na ![]() . Wykaż, że
. Wykaż, że ![]() jest procesem Wienera na całej półprostej.
jest procesem Wienera na całej półprostej.
Ćwiczenie 1.13
Udowodnij Twierdzenie 1.4.
Wykaż wpierw, że jeśli funkcja ![]() jest różniczkowalna w jakimś punkcie przedziału
jest różniczkowalna w jakimś punkcie przedziału ![]() , to
, to




