Zagadnienia

10.1 Rozkład Dooba-Meyera
10.2 Całka izometryczna
10.3 Uogólnienie definicji całki
10.4 Zadania

10. Całka względem ciągłych martyngałów

Podczas wcześniejszych wykładów zdefiniowaliśmy całkę $\int XdW$ . Okazuje się, że bez większych trudności definicję tę daje się uogólnić na $\int XdM$ , gdzie $M$ jest ciągłym martyngałem (a nawet ciągłym martyngałem lokalnym).

10.1. Rozkład Dooba-Meyera

Podstawą konstrukcji całki stochastycznej względem procesu Wienera jest to, że $W_{t}$ i $W_{t}^{2}-t$ są martyngałami. Okazuje się, że dla dowolnego całkowalnego z kwadratem ciągłego martyngału $M$ znajdzie się proces niemalejący $X$ taki, że $M^{2}-X$ jest martyngałem.

Twierdzenie 10.1 (rozkład Dooba-Meyera)

Dla $M\in{\mathcal{M}}^{{2,c}}_{T}$ istnieje proces $\langle M\rangle=(\langle M\rangle _{{t}})_{{0\leq t\leq T}}$ o trajektoriach ciągłych, niemalejących taki, że $\langle M\rangle _{0}=0$ oraz $(M^{2}_{t}-\langle M\rangle _{t})_{{0\leq t\leq T}}$ jest martyngałem. Co więcej proces $\langle M\rangle$ jest wyznaczony jednoznacznie.

Udowodnimy jednoznaczność rozkładu, dowód istnienia można znaleźć w [5].

Dowód Jednoznaczności

Załóżmy, że procesy $Y_{t},Z_{t}$ są niemalejące oraz $M_{t}^{2}-Y_{t}$ i $M_{t}^{2}-Z_{t}$ są martyngałami o ciągłych trajektoriach. Trajektorie procesu $Y_{t}-Z_{t}$ mają wahanie skończone, ponadto $Y_{t}-Z_{t}=(M_{t}^{2}-Z_{t})-(M_{t}^{2}-Y_{t})$ jest martyngałem ciągłym. Stąd, na podstawie Twierdzenia 7.3, $Y-Z\equiv 0$ .

∎

Przykład 10.1

Dla procesu Wienera $\langle W\rangle _{t}=t$ .
Ogólniej, Wniosek 9.1 implikuje, że $\langle\int X_{s}\, dW_{s}\rangle _{t}=\int _{0}^{t}X_{s}^{2}\, ds$ dla $X\in{\mathcal{L}}_{T}^{2}$ .

10.2. Całka izometryczna

Ponieważ dla wszystkich $\omega$ , $t\rightarrow\langle M\rangle _{t}(\omega)$ jest niemalejące, zatem ma wahanie skończone, czyli można określić skończoną miarę $d\langle M\rangle _{t}(\omega)$ na $[0,T]$ . Z uwagi na ciągłość $\langle M\rangle$ miara ta jest bezatomowa. Następna definicja jest naturalnym uogólnieniem definicji dla procesu Wienera.

Definicja 10.1

Dla procesu elementarnego $X$ postaci

$X=\xi _{0}{\mathrm{I}}_{{\{ 0\}}}+\sum _{{k=0}}^{{m-1}}\xi _{k}{\mathrm{I}}_{{(t_{k},t_{{k+1}}]}},$

gdzie $0=t_{0}\leq t_{1}\leq t_{2}\leq\ldots\leq t_{{m}}<T$ , $\xi _{k}$ ograniczone, ${\mathcal{F}}_{{t_{k}}}$ - mierzalne oraz $M\in{\mathcal{M}}^{{2,c}}_{T}$ określamy

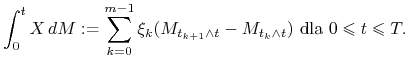$\int _{0}^{t}X\, dM:=\sum _{{k=0}}^{{m-1}}\xi _{k}(M_{{t_{{k+1}}\wedge t}}-M_{{t_{k}\wedge t}})\mbox{ dla }0\leq t\leq T.$

Definiujemy też dla $M\in{\mathcal{M}}^{{2,c}}_{T}$ ,

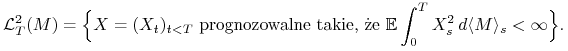${\mathcal{L}}_{T}^{2}(M)=\Big\{ X=(X_{{t}})_{{t<T}}\mbox{ prognozowalne takie, że }{\mathbb{E}}\int _{0}^{T}X_{s}^{2}\, d\langle M\rangle _{s}<\infty\Big\}.$

Stwierdzenie 10.1

Niech $M\in{\mathcal{M}}^{{2,c}}$ oraz $X\in{\mathcal{E}}$ . Wówczas $I(X):=\int X\, dM\in{\mathcal{M}}_{T}^{{2,c}}$ , $I(X)_{0}=0$ oraz

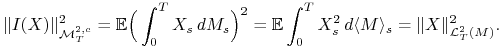$\| I(X)\| _{{{\mathcal{M}}_{T}^{{2,c}}}}^{2}={\mathbb{E}}\Big(\int _{0}^{T}X_{s}\, dM_{s}\Big)^{2}={\mathbb{E}}\int _{0}^{T}X_{s}^{2}\, d\langle M\rangle _{s}=\| X\| _{{{\mathcal{L}}_{T}^{2}(M)}}^{2}.$

Ciągłość $I(X)$ , warunek $I(X)_{0}=0$ oraz to, że $I(X)_{t}\in L_{2}$ dla wszystkich $t$ są oczywiste. Dla $t_{j}\leq t\leq t_{{j+1}}$ mamy

$I(X)_{t}=\xi _{0}(M_{{t_{1}}}-M_{{t_{0}}})+\xi _{1}(M_{{t_{2}}}-M_{{t_{1}}})+\ldots+\xi _{j}(M_{t}-M_{{t_{{j}}}}).$

Dla $t_{j}\leq t\leq s\leq t_{{j+1}}$ otrzymujemy zatem

${\mathbb{E}}(I(X)_{s}|{\mathcal{F}}_{t})-I(X)_{t}={\mathbb{E}}(\xi _{j}(M_{s}-M_{t})|{\mathcal{F}}_{t})=\xi _{j}({\mathbb{E}}(M_{s}|{\mathcal{F}}_{t})-M_{t})=0,$

czyli $I(X)$ jest martyngałem. Ponadto

	$\displaystyle{\mathbb{E}}I(X)_{T}^{2}=$	$\displaystyle\sum _{{k=0}}^{{m-1}}{\mathbb{E}}[\xi _{k}^{2}(M_{{t_{{k+1}}}}-M_{{t_{k}}})^{2}]$
		$\displaystyle+2\sum _{{j<k}}{\mathbb{E}}[\xi _{{k-1}}\xi _{{j-1}}(M_{{t_{k}}}-M_{{t_{{k-1}}}})(M_{{t_{j}}}-M_{{t_{{j-1}}}})]=:I_{1}+I_{2}.$

Zauważmy, że dla $s<t$ ,

	$\displaystyle{\mathbb{E}}((M_{t}-M_{s})^{2}\|$	$\displaystyle{\mathcal{F}}_{s})$
		$\displaystyle={\mathbb{E}}(M_{{t}}^{2}-\langle M\rangle _{t}\|{\mathcal{F}}_{s})+{\mathbb{E}}(\langle M\rangle _{t}\|{\mathcal{F}}_{s})-2M_{s}{\mathbb{E}}(M_{s}\|{\mathcal{F}}_{s})+M_{{s}}^{2}$
		$\displaystyle=M_{{s}}^{2}-\langle M\rangle _{s}+{\mathbb{E}}(\langle M\rangle _{t}\|{\mathcal{F}}_{s})-M_{s}^{2}={\mathbb{E}}(\langle M\rangle _{t}-\langle M\rangle _{s}\|{\mathcal{F}}_{s}).$

Stąd

	$\displaystyle I_{1}$	$\displaystyle=\sum _{k}{\mathbb{E}}[\xi _{k}^{2}{\mathbb{E}}((M_{{t_{{k+1}}}}-M_{{t_{k}}})^{2}\|{\mathcal{F}}_{{t_{k}}})]=\sum _{k}{\mathbb{E}}[\xi _{k}^{2}{\mathbb{E}}(\langle M\rangle _{{t_{{k+1}}}}-\langle M\rangle _{{t_{k}}}\|{\mathcal{F}}_{{t_{k}}})]$
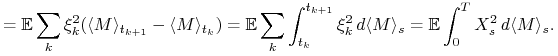		$\displaystyle={\mathbb{E}}\sum _{{k}}\xi _{k}^{2}(\langle M\rangle _{{t_{{k+1}}}}-\langle M\rangle _{{t_{k}}})={\mathbb{E}}\sum _{k}\int _{{t_{k}}}^{{t_{{k+1}}}}\xi _{k}^{2}\, d\langle M\rangle _{s}={\mathbb{E}}\int _{0}^{T}X_{s}^{2}\, d\langle M\rangle _{s}.$

Ponadto

$I_{2}=2\sum _{{j<k}}{\mathbb{E}}[\xi _{{k-1}}\xi _{{j-1}}(M_{{t_{j}}}-M_{{t_{{j-1}}}}){\mathbb{E}}(M_{{t_{k}}}-M_{{t_{{k-1}}}}|{\mathcal{F}}_{{t_{{k-1}}}})]=0.$

∎

Tak jak dla procesu Wienera dowodzimy, że domknięcie ${\mathcal{E}}$ w przestrzeni $L_{2}([0,T)\times\Omega,d\langle M\rangle\otimes{\mathbb{P}})$ jest równe $\overline{{\mathcal{E}}}={\mathcal{L}}_{T}^{2}(M)$ . Izometrię $I(X)$ możemy przedłużyć do $\overline{{\mathcal{E}}}$ , w ten sposób otrzymujemy izometryczną definicję całki $I(X)=\int X\, dM$ dla $X\in{\mathcal{L}}_{T}^{2}(M)$ . Mamy zatem następujący fakt.

Stwierdzenie 10.2

Niech $M\in{\mathcal{M}}^{{2,c}}_{T}$ . Wówczas
a) Dla $X\in{\mathcal{L}}_{T}^{2}(M)$ proces $\int XdM\in{\mathcal{M}}^{{2,c}}_{T}$ oraz

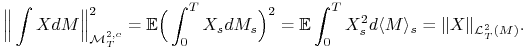$\Big\|\int XdM\Big\| _{{{\mathcal{M}}^{{2,c}}_{T}}}^{2}={\mathbb{E}}\Big(\int _{0}^{T}X_{s}dM_{s}\Big)^{2}={\mathbb{E}}\int _{{0}}^{T}X_{s}^{2}d\langle M\rangle _{s}=\| X\| _{{{\mathcal{L}}_{T}^{2}(M)}}.$

b) Jeśli $X,Y\in{\mathcal{L}}_{T}^{2}(M)$ , to $aX+bY\in{\mathcal{L}}_{T}^{2}(M)$ dla $a,b\in{\mathbb{R}}$ oraz $\int(aX+bY)dM=a\int XdM+b\int YdM$ .

10.3. Uogólnienie definicji całki

Zacznijmy od prostego faktu.

Stwierdzenie 10.3

Załóżmy, że $M\in{\mathcal{M}}^{{2,c}}_{T}$ , wówczas dla dowolnego momentu zatrzymania $\tau$ , $M^{{\tau}}\in{\mathcal{M}}^{{2,c}}_{T}$ oraz $\langle M^{{\tau}}\rangle=\langle M\rangle^{{\tau}}$ .

Wiemy, że $M^{{\tau}}$ jest ciągłym martyngałem. Na mocy nierówności Jensena

${\mathbb{E}}|M^{{\tau}}_{T}|^{2}={\mathbb{E}}M^{2}_{{\tau\wedge T}}={\mathbb{E}}[{\mathbb{E}}(M_{T}|{\mathcal{F}}_{{\tau\wedge T}})]^{2}\leq{\mathbb{E}}M_{T}^{2},$

zatem $M^{{\tau}}\in{\mathcal{M}}^{{2,c}}_{T}$ . Proces $\langle M\rangle^{{\tau}}$ startuje z zera, ma trajektorie ciągłe, ponadto $(M^{{\tau}})^{2}-\langle M\rangle^{{\tau}}=(M^{2}-\langle M\rangle)^{{\tau}}$ jest martyngałem, więc $\langle M\rangle^{{\tau}}$ spełnia wszystkie warunki definicji $\langle M^{{\tau}}\rangle$ .

∎

Możemy uogólnić rozkład Dooba-Meyera na przypadek ciągłych martyngałów lokalnych.

Wniosek 10.1

Załóżmy, że $M\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ , wówczas istnieje dokładnie jeden proces $\langle M\rangle=(\langle M\rangle _{t})_{{0\leq t<T}}$ o trajektoriach ciągłych, niemalejących taki, że $\langle M\rangle _{0}=0$ oraz $M^{2}-\langle M\rangle\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ .

Istnienie. Niech $\tau _{n}$ będzie rosnącym do $T$ ciągiem momentów zatrzymania takim, że $M^{{\tau _{n}}}\in{\mathcal{M}}_{T}^{{2,c}}$ . Określmy $Y_{n}:=\langle M^{{\tau _{n}}}\rangle$ , wówczas dla $n\leq m$ ,

$Y_{m}^{{\tau _{n}}}=\langle M^{{\tau _{m}}}\rangle^{{\tau _{n}}}=\langle(M^{{\tau _{m}}})^{{\tau _{n}}}\rangle=\langle M^{{\tau _{n}\wedge\tau _{m}}}\rangle=\langle M^{{\tau _{n}}}\rangle=Y_{n}.$

Stąd istnieje proces ciągły $Y=(Y_{t})_{{0\leq t<T}}$ taki, że $Y^{{\tau _{n}}}=Y_{n}$ , oczywiście $Y_{0}=Y_{{n,0}}=0$ , ponadto $Y$ ma trajektorie niemalejące oraz

$(M^{2}-Y)^{{\tau _{n}}}=(M^{{\tau _{n}}})^{2}-Y^{{\tau _{n}}}=(M^{{\tau _{n}}})^{2}-\langle M^{{\tau _{n}}}\rangle\in{\mathcal{M}}^{{c}},$

zatem $M^{2}-Y$ jest ciągłym martyngałem lokalnym na $[0,T)$ .

Jednoznaczność. Niech $Y$ i $\bar{Y}$ procesy ciągłe o niemalejących trajektoriach takie, że $Y_{0}=\bar{Y}_{0}=0$ oraz $M^{2}-Y$ i $M^{2}-\bar{Y}$ są martyngałami lokalnymi. Wówczas istnieją momenty zatrzymania $\tau _{n}\nearrow T$ i $\bar{\tau}_{n}\nearrow T$ takie, że $(M^{2}-Y)^{{\tau _{n}}}$ oraz $(M^{2}-\bar{Y})^{{\bar{\tau}_{n}}}$ są martyngałami. Biorąc $\sigma _{n}=\tau _{n}\wedge\bar{\tau}_{n}\nearrow T$ dostajemy martyngały $(M^{2}-Y)^{{\sigma _{n}}}=((M^{2}-Y)^{{\tau _{n}}})^{{\bar{\tau}_{n}}}$ oraz $(M^{2}-\bar{Y})^{{\sigma _{n}}}=((M^{2}-\bar{Y})^{{\bar{\tau}_{n}}})^{{\tau _{n}}}$ , proces $(Y-\bar{Y})^{{\sigma _{n}}}$ jest więc martyngałem o ograniczonym wahaniu, czyli jest stały, zatem $Y^{{\sigma _{n}}}=\bar{Y}^{{\sigma _{n}}}$ . Przechodząc z $n\rightarrow\infty$ otrzymujemy $Y=\bar{Y}.$

∎

Podobnie jak dla procesu Wienera dowodzimy twierdzenie o zatrzymaniu całki stochastycznej względem martyngałów całkowalnych z kwadratem.

Twierdzenie 10.2

Załóżmy, że $M\in{\mathcal{M}}^{{2,c}}_{T}$ , $X\in{\mathcal{L}}_{T}^{2}(M)$ oraz $\tau$ jest momentem zatrzymania. Wówczas ${\mathrm{I}}_{{[0,\tau]}}X\in{\mathcal{L}}_{T}^{2}(M)$ , $X\in{\mathcal{L}}_{T}^{2}(M^{{\tau}})$ oraz

$\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}(s)X_{s}\, dM_{s}=\int _{{0}}^{{t\wedge\tau}}X_{s}\, dM_{s}=\int _{0}^{t}X_{s}dM^{{\tau}}_{s}\quad\mbox{ dla }0\leq t\leq T.$

Definicja 10.2

Dla $T\leq\infty$ , $M\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ określamy przestrzeń procesów prognozowalnych, lokalnie całkowalnych z kwadratem względem $\langle M\rangle$

$\Lambda^{2}_{T}(M)=\Big\{(X_{t})_{{t<T}}-\mbox{ prognozowalny}\colon\ \int _{0}^{t}X_{s}^{2}\, d\langle M\rangle _{s}<\infty\mbox{ p.n. dla }t<T\Big\}.$

Ponieważ $\int XdM=\int Xd(M-M_{0})$ oraz $\langle M-M_{0}\rangle=\langle M\rangle$ , więc bez straty ogólności przy uogólnianiu definicji całki będziemy zakładać, że $M_{0}=0$ .

Definicja 10.3

Niech $M=(M_{t})_{{t<T}}\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ , $M_{0}=0$ , $X=(X_{t})_{{t<T}}\in\Lambda^{2}_{T}(M)$ oraz $\tau _{n}$ będzie rosnącym do $T$ ciągiem momentów zatrzymania takich, że $M^{{\tau _{n}}}\in{\mathcal{M}}^{{2,c}}_{T}$ i ${\mathrm{I}}_{{[0,\tau _{n}]}}X\in{\mathcal{L}}_{T}^{2}(M^{{\tau _{n}}})$ dla wszystkich $n$ . Całką stochastyczną $\int X\, dM$ nazywamy taki proces $(N_{t})_{{t<T}}=(\int _{0}^{t}X\, dM)_{{t<T}}$ , że $N^{{\tau _{n}}}_{t}=\int _{0}^{t}{\mathrm{I}}_{{[0,\tau _{n}]}}X\, dM^{{\tau _{n}}}$ dla $n=1,2,\ldots$ .

Nietrudno udowodnić (naśladując dowód dla całki względem procesu Wienera), że całka $\int X\, dM$ dla $M\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ i $X\in\Lambda^{2}_{T}(M)$ jest zdefiniowana poprawnie i jednoznacznie (z dokładnością do nieodróżnialności procesów) oraz nie zależy od wyboru ciągu momentów zatrzymania $\tau _{n}$ .

Następujący fakt przedstawia podstawowe własności $\int XdM$ .

Stwierdzenie 10.4

Niech $M,N\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ . Wówczas
a) Dla $X\in\Lambda _{T}^{2}(M)$ proces $\int XdM\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ .
b) Jeśli $X,Y\in\Lambda _{T}^{2}(M)$ , to $aX+bY\in\Lambda _{T}^{2}(M)$ dla $a,b\in{\mathbb{R}}$ oraz $\int(aX+bY)dM=a\int XdM+b\int YdM$ .
c) Jeśli $X\in\Lambda _{T}^{2}(M)\cap\Lambda _{T}^{2}(N)$ oraz $a,b\in{\mathbb{R}}$ , to $X\in\Lambda _{T}^{2}(aM+bN)$ oraz $\int Xd(aM+bN)=a\int XdM+b\int XdN$ .

Można również sformułować twierdzenie o zatrzymaniu całki stochastycznej w ogólnym przypadku.

Twierdzenie 10.3

Załóżmy, że $M\in{\mathcal{M}}^{{c}}_{{{\rm loc}}}$ , $X\in\Lambda _{T}^{2}(M)$ oraz $\tau$ będzie momentem zatrzymania. Wówczas ${\mathrm{I}}_{{[0,\tau]}}X\in\Lambda _{T}^{2}(M)$ , $X\in\Lambda _{T}^{2}(M^{{\tau}})$ oraz

$\int _{0}^{t}{\mathrm{I}}_{{[0,\tau]}}(s)\, dM_{s}=\int _{{0}}^{{t\wedge\tau}}X_{s}\, dM_{s}=\int _{0}^{t}X_{s}dM^{{\tau}}_{s}\quad\mbox{ dla }0\leq t<T.$

10.4. Zadania

Ćwiczenie 10.1

Niech $M=\int W_{t}^{2}dW_{t}$ . Oblicz ${\mathbb{E}}M_{s}^{2}$ . Jak wygląda przestrzeń ${\cal L}^{2}_{T}(M)$ ? Czy $W_{t}^{{-1}}$ należy do tej przestrzeni?

Ćwiczenie 10.2

Udowodnij Twierdzenia 10.2 i 10.3.

Ćwiczenie 10.3

Udowodnij Stwierdzenie 10.4.

Ćwiczenie 10.4

Załóżmy, że $X$ jest procesem ciągłym, a $M$ ciągłym martyngałem lokalnym. Wykaż, że jeśli $t<T$ , $\Pi _{n}=(t_{0}^{{(n)}},t_{1}^{{(n)}},\ldots,t_{{k_{n}}}^{{(n)}})$ jest ciągiem podziałów $[0,t]$ takim, że $0=t_{0}^{{(n)}}\leq t_{1}^{{(n)}}\leq\ldots\leq t_{{k_{n}}}^{{(n)}}=t$ oraz $\mathrm{diam}(\Pi _{n})\rightarrow 0$ , to

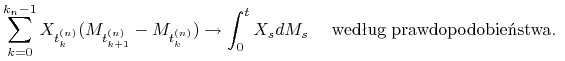$\sum _{{k=0}}^{{k_{n}-1}}X_{{{t_{k}^{{(n)}}}}}(M_{{t_{{k+1}}^{{(n)}}}}-M_{{t_{k}^{{(n)}}}})\rightarrow\int _{0}^{t}X_{s}dM_{s}\quad\mbox{ według prawdopodobieństwa. }$

Ćwiczenie 10.5

Wykaż, że każdy ciągły martyngał lokalny $M=(M_{t})_{{t<T}}$ , którego trajektorie mają skończone wahanie na każdym przedziale $[0,t]$ jest stale równy $M_{0}$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

	$\displaystyle{\mathbb{E}}((M_{t}-M_{s})^{2}\|$	$\displaystyle{\mathcal{F}}_{s})$
		$\displaystyle={\mathbb{E}}(M_{{t}}^{2}-\langle M\rangle _{t}\|{\mathcal{F}}_{s})+{\mathbb{E}}(\langle M\rangle _{t}\|{\mathcal{F}}_{s})-2M_{s}{\mathbb{E}}(M_{s}\|{\mathcal{F}}_{s})+M_{{s}}^{2}$
		$\displaystyle=M_{{s}}^{2}-\langle M\rangle _{s}+{\mathbb{E}}(\langle M\rangle _{t}\|{\mathcal{F}}_{s})-M_{s}^{2}={\mathbb{E}}(\langle M\rangle _{t}-\langle M\rangle _{s}\|{\mathcal{F}}_{s}).$

Wstęp do Analizy Stochastycznej