Zagadnienia

11.1 Nawias skośny jako wariacja kwadratowa
11.2 Uogólnienie definicji nawiasu skośnego
11.3 Zadania

11. Własności nawiasu skośnego

Podczas tego wykładu zajmiemy się interpretacją procesu $\langle M\rangle$ . Wprowadzimy też definicję nawiasu skośnego pary ciągłych martyngałów lokalnych.

11.1. Nawias skośny jako wariacja kwadratowa

Niech $\Pi=(t_{0},t_{1},\ldots,t_{k})$ będzie podziałem $[0,t]$ takim, że $0=t_{0}\leq t_{1}\leq\ldots\leq t_{k}=t$ . Definiujemy wówczas

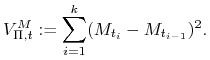$V_{{\Pi,t}}^{M}:=\sum _{{i=1}}^{k}(M_{{t_{i}}}-M_{{t_{{i-1}}}})^{2}.$

Będziemy też czasem pisać $V_{{\Pi,t}}(M)$ zamiast $V_{{\Pi,t}}^{M}$ . Pokażemy, że $\langle M\rangle _{t}$ jest granicą $V_{{\Pi,t}}^{M}$ przy $\mathrm{diam}(\Pi)\rightarrow 0$ , dlatego też $\langle M\rangle$ nazywa się często wariacją kwadratową $M$ .

Zacznijmy od najprostszej sytuacji martyngałów ograniczonych, tzn. takich, że $\sup _{t}\| M_{t}\| _{{\infty}}<\infty$ .

Twierdzenie 11.1

Załóżmy, że $M$ jest ograniczonym martyngałem ciągłym Wówczas $V_{{\Pi,t}}^{M}\rightarrow\langle M\rangle _{t}$ w $L_{2}(\Omega)$ dla $t\leq T$ , gdy $\mathrm{diam}(\Pi)\rightarrow 0$ .

Możemy założyć, rozpatrując zamiast $M$ proces $M-M_{0}$ , że $M_{0}=0$ , bo $V_{{\Pi,t}}(M-M_{0})=V_{{\Pi,t}}(M)$ oraz $\langle M-M_{0}\rangle=\langle M\rangle$ ( $(M-M_{0})^{2}-\langle M\rangle=(M^{2}-\langle M\rangle)-2MM_{0}+M_{0}^{2}$ jest martyngałem, czyli, z jednoznaczności $\langle\cdot\rangle$ , mamy $\langle M-M_{0}\rangle=\langle M\rangle$ ).

Niech $\Pi _{n}=(0=t_{0}^{{(n)}}\leq t_{1}^{{(n)}}\leq\ldots\leq t_{{k_{n}}}^{{(n)}}=t)$ będzie ciągiem podziałów $[0,t]$ takim, że $\mathrm{diam}(\Pi _{n})\rightarrow 0$ .

Połóżmy $C=\sup _{{s\leq T}}\| M_{s}\| _{{\infty}}$ . Liczymy

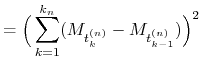	$\displaystyle M_{t}^{2}$	$\displaystyle=\Big(\sum _{{k=1}}^{{k_{n}}}(M_{{t_{k}^{{(n)}}}}-M_{{t_{{k-1}}^{{(n)}}}})\Big)^{2}$
		$\displaystyle=\sum _{k}(M_{{t_{k}^{{(n)}}}}-M_{{t_{{k-1}}^{{(n)}}}})^{2}+2\sum _{{k<j}}(M_{{t_{k}^{{(n)}}}}-M_{{t_{{k-1}}^{{(n)}}}})(M_{{t_{j}^{{(n)}}}}-M_{{t_{{j-1}}^{{(n)}}}})$
		$\displaystyle=V_{{\Pi _{n},t}}^{M}+2\sum _{{j}}(M_{{t_{j}^{{(n)}}}}-M_{{t_{{j-1}}^{{(n)}}}})M_{{t_{{j-1}}^{{(n)}}}}=V_{{\Pi _{n},t}}^{M}+2N_{n}(t).$

Niech

$X_{n}(s):=\sum _{{j=1}}^{{k_{n}}}M_{{t_{{j-1}}^{{(n)}}}}{\mathrm{I}}_{{(t_{{j-1}}^{{(n)}},t_{{j}}^{{(n)}}]}}\in{\mathcal{E}},$

wówczas $N_{n}(t)=\int _{0}^{t}X_{n}(s)\, dM_{s}.$ Z ciągłości $M$ dostajemy $X_{n}(s)\rightarrow M_{s}$ dla wszystkich $s\leq t$ . Ponadto $|X_{n}|\leq C$ , stąd $|X_{n}-M|^{2}\leq 4C^{2}$ i na mocy twierdzenia Lebesgue'a o zbieżności zmajoryzowanej,

${\mathbb{E}}\int _{0}^{t}|X_{n}-M|^{2}\, d\langle M\rangle _{s}\rightarrow 0.$

Zatem $X_{n}\rightarrow M$ w ${\mathcal{L}}_{t}^{2}(M)$ , czyli $N_{n}\rightarrow\int M\, dM$ w ${\mathcal{M}}_{t}^{{2,c}}$ , to znaczy $N_{n}(t)\rightarrow\int _{0}^{t}M_{s}\, dM_{s}$ w $L_{2}(\Omega)$ . Wykazaliśmy zatem, iż

$V_{{\Pi _{n},t}}^{M}=M_{t}^{2}-2N_{n}(t)\rightarrow M_{t}^{2}-2\int M\, dM\,\mbox{ w }L_{2}(\Omega).$

Proces $Y:=M^{2}-2\int M\, dM$ jest ciągły, $Y_{0}=0$ oraz $M^{2}-Y=2\int M\, dM$ jest martyngałem. By zakończyć dowód, że $Y=\langle M\rangle$ musimy wykazać monotoniczność trajektorii $Y$ . Wybierzmy $s<t$ i rozpatrzmy taki ciąg podziałów $\Pi _{n}$ odcinka $[0,t]$ , że $s$ jest jednym z punktów każdego z podziałów. Wówczas $\Pi _{n}$ można też traktować jako ciąg podziałów $[0,s]$ i określić $V_{{\Pi _{n},s}}^{M}$ . Mamy

$Y_{s}\stackrel{L_{2}}{\longleftarrow}V_{{\Pi _{n},s}}^{M}\leq V_{{\Pi _{n},t}}^{M}\stackrel{L_{2}}{\longrightarrow}Y_{t},$

czyli proces $Y$ ma trajektorie monotoniczne.

∎

Uwaga 11.1

W szczególności przedstawiony dowód pokazuje, że dla martyngału jednostajnie ograniczonego $M$ , takiego, że $M_{0}=0$ , zachodzi $M^{2}=2\int M\, dM+\langle M\rangle$ .

By uogólnić Twierdzenie 11.1 na przypadek martyngałów całkowalnych z kwadratem będziemy potrzebowali dwóch faktów.

Lemat 11.1

Niech $(\xi _{n})$ będzie ciągiem zmiennych losowych, a $(A_{k})$ wstępującym ciągiem zdarzeń takim, że ${\mathbb{P}}(\bigcup A_{k})=1$ . Załóżmy, że dla wszystkich $k$ , zmienne $\xi _{n}{\mathrm{I}}_{{A_{k}}}$ zbiegają według prawdopodobieństwa (przy $n\rightarrow\infty$ ) do zmiennej $\eta _{k}$ . Wówczas $\xi _{n}$ zbiega według prawdopodobieństwa do zmiennej $\eta$ takiej, że $\eta{\mathrm{I}}_{{A_{{k}}}}=\eta _{k}$ p.n. dla $k=1,2,\ldots$ .

Dla $k\leq l$ mamy $\eta _{l}{\mathrm{I}}_{{A_{k}}}=\eta _{k}$ p.n., gdyż pewien podciąg $\xi _{{n_{s}}}{\mathrm{I}}_{{A_{l}}}\rightarrow\eta _{l}$ p.n., a zatem $\xi _{{n_{s}}}{\mathrm{I}}_{{A_{l}}}=\xi _{{n_{s}}}{\mathrm{I}}_{{A_{l}}}{\mathrm{I}}_{{A_{k}}}\rightarrow\eta _{l}{\mathrm{I}}_{{A_{k}}}$ p.n. (czyli również wg ${\mathbb{P}}$ ). Stąd istnieje zmienna losowa $\eta$ taka, że $\eta{\mathrm{I}}_{{A_{k}}}=\eta _{k}$ p.n..

Zauważmy, że ${\mathbb{P}}(A_{k}^{{c}})\leq\varepsilon/2$ dla dużego $k$ oraz przy ustalonym $k$ , ${\mathbb{P}}(|\xi _{n}{\mathrm{I}}_{{A_{k}}}-\eta _{k}|\geq\varepsilon)\leq\varepsilon/2$ dla dużych $n$ , stąd

${\mathbb{P}}(|\xi _{n}-\eta|\geq\varepsilon)\leq{\mathbb{P}}(A_{k}^{{c}})+{\mathbb{P}}(|\xi _{n}{\mathrm{I}}_{{A_{k}}}-\eta{\mathrm{I}}_{{A_{k}}}|\geq\varepsilon)\leq\varepsilon$

dla dostatecznie dużych $n$ .

∎

Kolejny lemat pokazuje, że przy pewnych prostych założeniach można ze zbieżności według prawdopodobieństwa wyprowadzić zbieżność w $L_{1}$ .

Lemat 11.2

Załóżmy, że $\xi _{n}\geq 0$ , $\xi _{n}\rightarrow\xi$ według ${\mathbb{P}}$ oraz dla wszystkich $n$ , ${\mathbb{E}}\xi _{n}={\mathbb{E}}\xi<\infty$ . Wówczas $\xi _{n}\rightarrow\xi$ w $L_{1}.$

Mamy

	$\displaystyle{\mathbb{E}}\|\xi-\xi _{n}\|$	$\displaystyle={\mathbb{E}}(\|\xi-\xi _{n}\|-(\xi-\xi _{n}))=2{\mathbb{E}}(\xi-\xi _{n}){\mathrm{I}}_{{\{\xi\geq\xi _{n}\}}}$
		$\displaystyle\leq\frac{\varepsilon}{2}+2{\mathbb{E}}(\xi-\xi _{n}){\mathrm{I}}_{{\{\xi\geq\xi _{n}+\frac{\varepsilon}{4}\}}}\leq\frac{\varepsilon}{2}+2{\mathbb{E}}\xi{\mathrm{I}}_{{\{\xi\geq\xi _{n}+\frac{\varepsilon}{4}\}}}.$

Na mocy zbieżności według prawdopodobieństwa, $\lim _{{n\rightarrow\infty}}{\mathbb{P}}(\xi\geq\xi _{n}+\varepsilon/4)=0$ . Ponadto ${\mathbb{E}}|\xi|={\mathbb{E}}\xi<\infty$ , zatem $\{\xi\}$ jest jednostajnie całkowalna , czyli $|{\mathbb{E}}\xi{\mathrm{I}}_{A}|\leq\varepsilon/2$ dla odpowiednio małego ${\mathbb{P}}(A)$ . Stąd ${\mathbb{E}}\xi{\mathrm{I}}_{{\{\xi\geq\xi _{n}+\varepsilon/4\}}}\leq\varepsilon/2$ dla dużych $n$ , a więc ${\mathbb{E}}|\xi-\xi _{n}|\leq\varepsilon$ .

∎

Twierdzenie 11.2

Załóżmy, że $M\in{\mathcal{M}}_{T}^{{2,c}}$ , wówczas dla $t<T$ , $V_{{\Pi,t}}^{M}\rightarrow\langle M\rangle _{t}$ w $L_{1}(\Omega)$ , gdy $\mathrm{diam}(\Pi)\rightarrow 0$ .

Jak poprzednio możemy zakładać, że $M_{0}=0$ . Ustalmy ciąg podziałów $\Pi _{n}$ taki, że $\mathrm{diam}(\Pi _{n})\rightarrow 0$ .

Istnieje ciąg momentów zatrzymania $\tau _{k}\nearrow T$ taki, że $M^{{\tau _{k}}}$ jest jednostajnie ograniczony (np. $\tau _{k}=\inf\{ t\colon|M_{t}|\leq k\}$ ). Na mocy Twierdzenia 11.1, dla ustalonego $k$ , mamy przy $n\rightarrow\infty$ ,

$V_{{\Pi _{n},t}}(M^{{\tau _{k}}})\stackrel{L_{2}}{\longrightarrow}\langle M^{{\tau _{k}}}\rangle _{t}=\langle M\rangle^{{\tau _{k}}}_{t}.$

Stąd

${\mathrm{I}}_{{\{ t\leq\tau _{k}\}}}V_{{\Pi _{n},t}}(M)={\mathrm{I}}_{{\{ t\leq\tau _{k}\}}}V_{{\Pi _{n},t}}(M^{{\tau _{k}}})\stackrel{L_{2}}{\longrightarrow}{\mathrm{I}}_{{\{ t\leq\tau _{k}\}}}\langle M\rangle _{t}^{{\tau _{k}}}={\mathrm{I}}_{{\{ t\leq\tau _{k}\}}}\langle M\rangle _{t}.$

Zbieżność w $L_{2}$ implikuje zbieżność według prawdopodobieństwa, zatem możemy stosować Lemat 11.1 do $\xi _{n}=V_{{\Pi _{n},t}}(M)$ i $A_{k}=\{ t\leq\tau _{k}\}$ , by otrzymać $V_{{\Pi _{n},t}}(M)\rightarrow\langle M\rangle _{t}$ według ${\mathbb{P}}$ . Mamy jednak

${\mathbb{E}}\langle M\rangle _{t}={\mathbb{E}}M_{t}^{2}={\mathbb{E}}[V_{{\Pi _{n},t}}(M)+2\sum _{j}M_{{t_{{j-1}}^{{(n)}}}}(M_{{t_{j}^{{(n)}}}}-M_{{t_{{j-1}}^{{(n)}}}})]={\mathbb{E}}V_{{\Pi _{n},t}}(M),$

a zatem na mocy Lematu 11.2, $V_{{\Pi _{n},t}}(M)\rightarrow\langle M\rangle _{t}$ w $L_{1}$ .

∎

Dla martyngałów lokalnych zachodzi zbliżone twierdzenie, tylko zbieżność w $L_{1}$ musimy zastąpić zbieżnością według prawdopodobieństwa.

Wniosek 11.1

Załóżmy, że $M\in{\mathcal{M}}_{{{\rm loc}}}^{{c}}$ , wówczas dla $t<T$ , $V_{{\Pi,t}}^{M}\rightarrow\langle M\rangle _{t}$ według prawdopodobieństwa, gdy $\mathrm{diam}(\Pi)\rightarrow 0$ .

Bez straty ogólności możemy założyć, że $M_{0}=0$ , wówczas $M\in{\mathcal{M}}_{{{\rm loc}}}^{{2,c}}$ . Niech $\Pi _{n}$ będą podziałami $[0,t]$ o średnicy zbieżnej do zera oraz $\tau _{k}\nearrow T$ takie, że $M^{{\tau _{k}}}\in{\mathcal{M}}^{{2,c}}$ . Na podstawie Twierdzenia 11.2 otrzymujemy, że dla ustalonego $k$ ,

$V_{{\Pi _{n},t}}(M^{{\tau _{k}}})\stackrel{L_{1}}{\longrightarrow}\langle M^{{\tau _{k}}}\rangle=\langle M\rangle^{{\tau _{k}}}.$

Stąd

$V_{{\Pi _{n},t}}(M){\mathrm{I}}_{{\{\tau _{k}\geq t\}}}=V_{{\Pi _{n},t}}(M^{{\tau _{k}}}){\mathrm{I}}_{{\{\tau _{k}\geq t\}}}\stackrel{L_{1}}{\longrightarrow}\langle M\rangle^{{\tau _{k}}}{\mathrm{I}}_{{\{\tau _{k}\geq t\}}}=\langle M\rangle{\mathrm{I}}_{{\{\tau _{k}\geq t\}}}.$

Teza wynika z Lematu 11.1.

∎

11.2. Uogólnienie definicji nawiasu skośnego

Nawias skośny określa się nie tylko dla pojedynczego martyngału, ale też i dla pary martyngałów.

Definicja 11.1

Nawiasem skośnym dwóch ciągłych martyngałów lokalnych $M$ i $N$ nazywamy proces $\langle M,N\rangle$ zdefiniowany wzorem

$\langle M,N\rangle=\frac{1}{4}[\langle M+N\rangle-\langle M-N\rangle].$

Stwierdzenie 11.1

a) Załóżmy, że $M,N\in{\mathcal{M}}^{{2,c}}_{T}$ , wówczas $\langle M,N\rangle$ to jedyny proces o trajektoriach ciągłych mających wahanie skończone na $[0,T]$ taki, że $\langle M,N\rangle _{0}=0$ oraz $MN-\langle M,N\rangle$ jest martyngałem na $[0,T]$ .
b) Załóżmy, że $M,N\in{\mathcal{M}}_{{{\rm loc}}}^{{c}}$ , wówczas $\langle M,N\rangle$ to jedyny proces o trajektoriach ciągłych mających wahanie skończone na $[0,t]$ dla $t<T$ taki, że $\langle M,N\rangle _{0}=0$ oraz $MN-\langle M,N\rangle$ jest martyngałem lokalnym na $[0,T)$ .

Jednoznaczność dowodzimy jak dla $\langle M\rangle$ , zaś wymienione własności wynikają z tożsamości

$MN-\langle M,N\rangle=\frac{1}{4}\Big[\Big((M+N)^{2}-\langle M+N\rangle\Big)-\Big((M-N)^{2}-\langle M-N\rangle\Big)\Big].$

∎

Stwierdzenie 11.2

Niech $\Pi _{n}=(t_{0}^{{(n)}},t_{1}^{{(n)}},\ldots,t_{{k_{n}}}^{{(n)}})$ będzie ciągiem podziałów $[0,t]$ takim, że $0=t_{0}^{{(n)}}\leq t_{1}^{{(n)}}\leq\ldots\leq t_{{k_{n}}}^{{(n)}}=t$ oraz $\mathrm{diam}(\Pi _{n})\rightarrow 0$ .
a) Jeśli $M,N\in{\mathcal{M}}^{{2,c}}_{T}$ , to dla $t<T$ ,

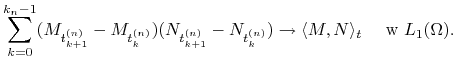$\sum _{{k=0}}^{{k_{n}-1}}(M_{{t_{{k+1}}^{{(n)}}}}-M_{{t_{k}^{{(n)}}}})(N_{{t_{{k+1}}^{{(n)}}}}-N_{{t_{k}^{{(n)}}}})\rightarrow\langle M,N\rangle _{t}\quad\mbox{ w }L_{1}(\Omega).$

b) Jeśli $M,N\in{\mathcal{M}}_{{{\rm loc}}}^{{2,c}}$ , to dla $t<T$ ,

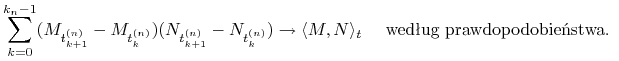$\sum _{{k=0}}^{{k_{n}-1}}(M_{{t_{{k+1}}^{{(n)}}}}-M_{{t_{k}^{{(n)}}}})(N_{{t_{{k+1}}^{{(n)}}}}-N_{{t_{k}^{{(n)}}}})\rightarrow\langle M,N\rangle _{t}\quad\mbox{ według prawdopodobieństwa. }$

Wystarczy zauważyć, że

$(M_{t}-M_{s})(N_{t}-N_{s})=\frac{1}{4}[((M_{t}+N_{t})-(M_{s}+N_{s}))^{2}-((M_{t}-N_{t})-(M_{s}-N_{s}))^{2}]$

i skorzystać z Twierdzenia 11.1 i Wniosku 11.1.

∎

Stwierdzenie 11.3

Dla dowolnych ciągłych martyngałów lokalnych $M$ i $N$ ,
a) $\langle M,M\rangle=\langle M\rangle=\langle-M\rangle$ ,
b) $\langle M,N\rangle=\langle N,M\rangle$ ,
c) $\langle M-M_{0},N\rangle=\langle M,N-N_{0}\rangle=\langle M-M_{0},N-N_{0}\rangle=\langle M,N\rangle$ ,
d) $(N,M)\rightarrow\langle M,N\rangle$ jest przekształceniem dwuliniowym,
e) $\langle M^{{\tau}},N^{{\tau}}\rangle=\langle M^{{\tau}},N\rangle=\langle M,N^{{\tau}}\rangle=\langle M,N\rangle^{{\tau}}$ dla każdego momentu zatrzymania $\tau$ ,
f) jeśli $X\in\Lambda _{{T}}^{2}(M)$ oraz $Y\in\Lambda _{{T}}^{2}(N)$ , to $\langle\int XdM,\int YdN\rangle=\int XYd\langle M,N\rangle.$

Szkic dowodu.

Punkty a), b) i c) wynikają natychmiast z definicji, punkt d) z Wniosku 11.1. To, że $\langle M^{{\tau}},N^{{\tau}}\rangle=\langle M,N\rangle^{{\tau}}$ dowodzimy jak w Stwierdzeniu 10.3 (wykorzystując Stwierdzenie 11.1). Pozostałe równości w e) wynikają ze Stwierdzenia 11.2. Punkt f) dowodzimy najpierw dla przypadku, gdy $M$ i $N$ są martyngałami, zaś $X$ i $Y$ procesami elementarnymi, następnie dla $X\in{\mathcal{L}}^{2}_{T}(M)$ oraz $Y\in{\mathcal{L}}^{2}_{T}(M)$ i wreszcie, wykorzystując własność e), dla przypadku ogólnego.

∎

11.3. Zadania

Ćwiczenie 11.1

Oblicz $\langle W^{{1}},W^{{2}}\rangle$ , gdzie $W^{{1}},W^{{2}}$ są niezależnymi procesy Wienera.

Ćwiczenie 11.2

Wykaż, że
a) $|\langle M,N\rangle|\leq\langle M\rangle\langle N\rangle$
b) ${\rm Wah}_{{[s,t]}}(\langle M,N\rangle)\leq\frac{1}{2}[\langle M\rangle _{t}-\langle M\rangle _{s}+\langle N\rangle _{t}-\langle N\rangle _{s}]$ .

Ćwiczenie 11.3

Uzupełnij dowód Stwierdzenia 11.3.

Ćwiczenie 11.4

Wykaż, że dla dowolnego procesu $M\in{\mathcal{M}}^{c}_{{\mathrm{loc}}}$ , $X\in\Lambda _{{2}}^{T}(M)$ oraz momentu zatrzymania $\tau\leq T$ ,

${\mathbb{E}}\sup _{{t<\tau}}\Big(\int _{0}^{t}X\, dM\Big)^{2}\leq 4{\mathbb{E}}\int _{0}^{{\tau}}X_{s}^{2}\, d\langle M\rangle _{s}.$

Ćwiczenie 11.5

Załóżmy, że $M\in{\mathcal{M}}^{c}_{{\mathrm{loc}}}$ , $M_{0}=0$ oraz $\tau$ jest momentem zatrzymania takim, że ${\mathbb{E}}\langle M\rangle _{{\tau}}<\infty$ . Wykaż, że $M^{{\tau}}$ jest martyngałem.

Ćwiczenie 11.6

Określamy

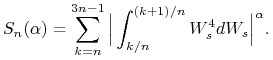$S_{n}(\alpha)=\sum _{{k=n}}^{{3n-1}}\Big|\int _{{k/n}}^{{(k+1)/n}}W_{s}^{4}dW_{s}\Big|^{{\alpha}}.$

a) Wykaż, że ciąg $S_{n}(2)$ jest zbieżny w $L_{1}$ i zidentyfikuj jego granicę.
b) Co można powiedzieć o zbieżności według prawdopodobieństwa ciągu $S_{n}(\alpha)$ dla $\alpha\neq 2$ ?

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do Analizy Stochastycznej