Zagadnienia
14. Stochastyczne Równania Różniczkowe
Z całką stochastyczną wiąże się pojęcie równania stochastycznego. Podamy kryteria istnienia i jednoznaczności rozwiązań takich równań oraz omówimy kilka przykładów.
14.1. Jednorodne równania stochastyczne
Definicja 14.1
Załóżmy, że ![]() są funkcjami ciągłymi, a
są funkcjami ciągłymi, a ![]() zmienną losową
zmienną losową
![]() -mierzalną. Mówimy, że proces
-mierzalną. Mówimy, że proces ![]() rozwiązuje
jednorodne równanie stochastyczne
rozwiązuje
jednorodne równanie stochastyczne
| (14.1) |
jeśli
Uwaga 14.1
Przyjeliśmy, że ![]() i
i ![]() są funkcjami ciągłymi, by
uniknąć problemów związanych z mierzalnością i lokalną ograniczonością
procesów
są funkcjami ciągłymi, by
uniknąć problemów związanych z mierzalnością i lokalną ograniczonością
procesów ![]() i
i ![]() . Rozważa się jednak również stochastyczne równania
różniczkowe z nieciągłymi współczynnikami.
. Rozważa się jednak również stochastyczne równania
różniczkowe z nieciągłymi współczynnikami.
Uwaga 14.2
Wprowadzając nowy proces ![]() ,
, ![]() oraz filtrację
oraz filtrację
![]() zamieniamy równanie różniczkowe (14.1)
na podobne równanie dla
zamieniamy równanie różniczkowe (14.1)
na podobne równanie dla ![]() z warunkiem początkowym
z warunkiem początkowym ![]() .
.
Definicja 14.2
Proces ![]() rozwiązujący równanie (14.1) nazywamy dyfuzją startująca z
rozwiązujący równanie (14.1) nazywamy dyfuzją startująca z ![]() . Funkcję
. Funkcję
![]() nazywamy współczynnikiem dyfuzji, a funkcję
nazywamy współczynnikiem dyfuzji, a funkcję ![]() współczynnikiem dryfu.
współczynnikiem dryfu.
Przypomnijmy, że funkcja ![]() jest lipschitzowska ze stałą
jest lipschitzowska ze stałą ![]() , jeśli
, jeśli
![]() dla wszystkich
dla wszystkich ![]() . Lipschitzowskość implikuje też, że
. Lipschitzowskość implikuje też, że
gdzie można przyjąć np. ![]() .
.
Twierdzenie 14.1
Załóżmy, że funkcje ![]() i
i ![]() są lipschitzowskie na
są lipschitzowskie na ![]() , wówczas równanie stochastyczne
(14.1)
ma co najwyżej jedno rozwiązanie (z dokładnością do nierozróżnialności).
, wówczas równanie stochastyczne
(14.1)
ma co najwyżej jedno rozwiązanie (z dokładnością do nierozróżnialności).
Bez straty ogólności możemy zakładać, że ![]() oraz
oraz ![]() są lipschitzowskie z tą
samą stałą
są lipschitzowskie z tą
samą stałą ![]() .
.
Załóżmy, że ![]() i
i ![]() są rozwiązaniami (14.1), wówczas
są rozwiązaniami (14.1), wówczas
Krok I. Załóżmy dodatkowo, że funkcja ![]() jest
skończona i ograniczona na przedziałach
jest
skończona i ograniczona na przedziałach ![]() ,
, ![]() .
.
Mamy
Z warunku Lipschitza i nierówności Schwarza,
By oszacować ![]() zauważmy, że
zauważmy, że ![]() ,
więc
,
więc ![]() .
Stąd
.
Stąd
Ustalmy ![]() , wówczas z powyższych oszacowań wynika, że
, wówczas z powyższych oszacowań wynika, że
gdzie ![]() .
Iterując powyższą nierówność dostajemy dla
.
Iterując powyższą nierówność dostajemy dla ![]() ,
,
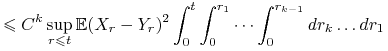 |
|||
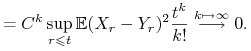 |
Stąd dla wszystkich ![]() ,
, ![]() , czyli
, czyli ![]() p.n., a więc z ciągłości
obu procesów,
p.n., a więc z ciągłości
obu procesów, ![]() i
i ![]() są nieodróżnialne.
są nieodróżnialne.
Krok II.![]() i
i ![]() dowolne.
Określmy
dowolne.
Określmy
i zauważmy, że ![]() . Ponieważ w zerze
oba procesy się pokrywają, więc
. Ponieważ w zerze
oba procesy się pokrywają, więc ![]() ,
stąd
,
stąd
![]() i
i ![]() dla
dla ![]() .
Mamy
.
Mamy
Naśladując rozumowanie z kroku I dostajemy ![]() p.n.,
przechodząc z
p.n.,
przechodząc z ![]() mamy
mamy ![]() p.n..
p.n..
Twierdzenie 14.2
Załóżmy, że funkcje ![]() i
i ![]() są lipschitzowskie na
są lipschitzowskie na ![]() oraz
oraz ![]() , wówczas
równanie stochastyczne (14.1) ma dokładnie jedno rozwiązanie
, wówczas
równanie stochastyczne (14.1) ma dokładnie jedno rozwiązanie ![]() .
Co więcej
.
Co więcej ![]() oraz funkcja
oraz funkcja ![]() jest ograniczona na przedziałach ograniczonych.
jest ograniczona na przedziałach ograniczonych.
Jak w poprzednim twierdzeniu zakładamy, że ![]() . Jednoznaczność rozwiązania już znamy. By
wykazać jego istnienie posłużymy się konstrukcją z użyciem metody kolejnych przybliżeń.
Określamy
. Jednoznaczność rozwiązania już znamy. By
wykazać jego istnienie posłużymy się konstrukcją z użyciem metody kolejnych przybliżeń.
Określamy
![]() oraz indukcyjnie
oraz indukcyjnie
| (14.2) |
Definicja jest poprawna (tzn. całki są dobrze określone), gdyż ![]() są procesami
ciągłymi, adaptowalnymi. Ponadto indukcyjnie pokazujemy, że funkcja
są procesami
ciągłymi, adaptowalnymi. Ponadto indukcyjnie pokazujemy, że funkcja
![]() jest ograniczona na przedziałach skończonych:
jest ograniczona na przedziałach skończonych:
Zatem ![]() , a więc również
, a więc również ![]() .
.
Zauważmy, że wobec nierówności ![]() i niezależności
i niezależności ![]() i
i ![]() ,
dla
,
dla ![]() zachodzi
zachodzi
gdzie ![]() .
Podobnie szacujemy dla
.
Podobnie szacujemy dla ![]() ,
,
gdzie ![]() . Iterując to szacowanie dostajemy
. Iterując to szacowanie dostajemy
Pokazaliśmy zatem, że ![]() dla
dla ![]() . Ponieważ szereg
. Ponieważ szereg ![]() jest zbieżny,
więc
jest zbieżny,
więc ![]() jest ciągiem Cauchy'ego w
jest ciągiem Cauchy'ego w ![]() , czyli jest zbieżny.
Z uwagi na jednostajność szacowań wykazaliśmy istnienie
, czyli jest zbieżny.
Z uwagi na jednostajność szacowań wykazaliśmy istnienie ![]() takiego, że
takiego, że
Stąd też wynika, że ![]() jest ograniczona na przedziałach ograniczonych.
jest ograniczona na przedziałach ograniczonych.
Wykażemy teraz, że ![]() z prawdopodobieństwem
z prawdopodobieństwem ![]() zbiega do
zbiega do ![]() niemal jednostajnie.
Zauważmy, że dla
niemal jednostajnie.
Zauważmy, że dla ![]() ,
,
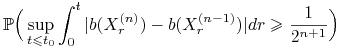 |
|||
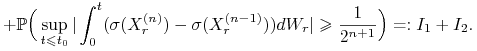 |
Mamy
Z nierównośći Dooba dla martyngału ![]() dostajemy
dostajemy
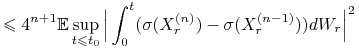 |
|||
Przyjmując
dostajemy
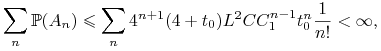 |
więc ![]() . Zatem dla
. Zatem dla ![]() , ciąg procesów
, ciąg procesów ![]() zbiega
jednostajnie na
zbiega
jednostajnie na ![]() z prawdopodobieństwem
z prawdopodobieństwem ![]() , czyli z prawdopodobieństwem
, czyli z prawdopodobieństwem ![]() zbiega niemal jednostajnie na
zbiega niemal jednostajnie na
![]() .
Ewentualnie modyfikując
.
Ewentualnie modyfikując ![]() i
i ![]() na zbiorze miary zero widzimy, że
na zbiorze miary zero widzimy, że ![]() jest
granicą niemal jednostajną
jest
granicą niemal jednostajną ![]() , czyli
, czyli ![]() ma trajektorie ciągłe.
ma trajektorie ciągłe.
Ze zbieżności ![]() do
do ![]() w
w ![]() , jednostajnej na
, jednostajnej na ![]() oraz lipschitzowskości
oraz lipschitzowskości
![]() i
i ![]() łatwo wynika zbieżność w
łatwo wynika zbieżność w ![]() ,
, ![]() i
i
![]() do odpowiednio
do odpowiednio ![]() i
i ![]() ,
zatem możemy przejść w (14.2) do granicy by otrzymać dla ustalonego
,
zatem możemy przejść w (14.2) do granicy by otrzymać dla ustalonego ![]()
Oba procesy ![]() i
i ![]() są ciągłe, zatem są nierozróżnialne.
są ciągłe, zatem są nierozróżnialne.
Przykład 14.1
Stosując wzór Itô łatwo sprawdzić, że proces
![]() jest rozwiązaniem
równania
jest rozwiązaniem
równania
Jest to jedyne rozwiązanie tego równania, gdyż ![]() oraz
oraz ![]() są
funkcjami lipschitzowskimi.
są
funkcjami lipschitzowskimi.
Przykład 14.2
Proces
jest rozwiązaniem równania
Jest to jedyne rozwiązanie, gdyż funkcje ![]() oraz
oraz ![]() są lipschitzowskie.
Jeśli
są lipschitzowskie.
Jeśli ![]() oraz
oraz ![]() ma rozkład
ma rozkład ![]() , to proces
, to proces ![]() jest stacjonarny
(proces Ornsteina-Uhlenbecka).
jest stacjonarny
(proces Ornsteina-Uhlenbecka).
14.2. Równania niejednorodne
Często współczynniki równania zależą nie tylko od ![]() , ale i od czasu.
, ale i od czasu.
Definicja 14.3
Załóżmy, że ![]() są funkcjami ciągłymi, a
są funkcjami ciągłymi, a ![]() zmienną losową
zmienną losową
![]() -mierzalną. Mówimy, że proces
-mierzalną. Mówimy, że proces ![]() rozwiązuje
równanie stochastyczne
rozwiązuje
równanie stochastyczne
| (14.3) |
jeśli
Dla równania niejednorodnego naturalne są następujące warunki Lipschitza
Twierdzenie 14.3
Załóżmy, że funkcje ![]() i
i ![]() spełniają warunki Lipschitza. Wówczas dla dowolnej
zmiennej
spełniają warunki Lipschitza. Wówczas dla dowolnej
zmiennej ![]() ,
, ![]() -mierzalnej takiej, że
-mierzalnej takiej, że ![]() istnieje dokładnie
jedno rozwiązanie (14.3). Co więcej rozwiązanie to daje się otrzymać metodą
kolejnych przybliżeń jak w przypadku jednorodnym.
istnieje dokładnie
jedno rozwiązanie (14.3). Co więcej rozwiązanie to daje się otrzymać metodą
kolejnych przybliżeń jak w przypadku jednorodnym.
Przykład 14.3
Równanie
| (14.4) |
spełnia założenia twierdzenia, jeśli ![]() . By znaleźć jego rozwiązanie
sformułujmy ogólniejszy fakt.
. By znaleźć jego rozwiązanie
sformułujmy ogólniejszy fakt.
Stwierdzenie 14.1
Załóżmy, że ![]() jest ciągłym martyngałem lokalnym, zaś
jest ciągłym martyngałem lokalnym, zaś ![]() zmienną
zmienną ![]() -mierzalną.
Wówczas proces
-mierzalną.
Wówczas proces ![]() jest martyngałem lokalnym takim, że
jest martyngałem lokalnym takim, że
![]() , tzn.
, tzn. ![]() .
.
Proces ![]() bywa nazywany eksponentą stochastyczną.
bywa nazywany eksponentą stochastyczną.
Z wzoru Itô dla semimartyngału ![]() dostajemy
dostajemy
Proces ![]() jest martyngałem lokalnym na mocy konstrukcji całki stochastycznej.
jest martyngałem lokalnym na mocy konstrukcji całki stochastycznej.
Wracając do Przykładu 14.3 zauważamy, że ![]() jest martyngałem lokalnym, więc
rozwiązanie równania (14.4) ma postać
jest martyngałem lokalnym, więc
rozwiązanie równania (14.4) ma postać
Przykład 14.4
Rozpatrzmy niejednorodne równanie liniowe postaci
Współczynniki ![]() i
i ![]() spełniają warunki Lipschitza, jeśli
spełniają warunki Lipschitza, jeśli
![]() oraz
oraz ![]() . By znaleźć rozwiązanie załóżmy, że jest
postaci
. By znaleźć rozwiązanie załóżmy, że jest
postaci ![]() , gdzie
, gdzie ![]() ,
, ![]() , postać
, postać ![]() znamy z Przykładu 3.
Wówczas, z dwuwymiarowego wzoru Itô
znamy z Przykładu 3.
Wówczas, z dwuwymiarowego wzoru Itô
Wystarczy więc rozwiązać zwyczajne równanie różniczkowe
by dostać
14.3. Przypadek wielowymiarowy
Zanim sformułujemy odpowiednik wcześniejszych wyników dla przypadku wielowymiarowego wprowadzimy wygodne ustalenia notacyjne.
Definicja 14.4
Niech ![]() będzie
będzie ![]() -wymiarowym procesem Wienera. Dla
-wymiarowym procesem Wienera. Dla
![]() macierzy
macierzy ![]() złożonej z procesów
z
złożonej z procesów
z ![]() określamy
określamy ![]() -wymiarowy proces
-wymiarowy proces
wzorem
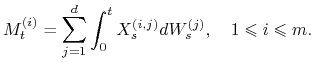 |
Przy powyżej wprowadzonej notacji możemy zdefiniować wielowymiarowe równania stochastyczne.
Definicja 14.5
Załóżmy, że ![]() są funkcjami ciągłymi,
są funkcjami ciągłymi, ![]() jest
jest ![]() -wymiarowym procesem Wienera,
a
-wymiarowym procesem Wienera,
a ![]() ,
, ![]() -wymiarowym,
-wymiarowym, ![]() -mierzalnym wektorem losowym.
Mówimy, że
-mierzalnym wektorem losowym.
Mówimy, że ![]() -wymiarowy proces
-wymiarowy proces ![]() rozwiązuje
jednorodne wielowymiarowe równanie stochastyczne
rozwiązuje
jednorodne wielowymiarowe równanie stochastyczne
jeśli
Tak jak w przypadku jednowymiarowym dowodzimy:
Twierdzenie 14.4
Załóżmy, że ![]() jest
jest ![]() -wymiarowym,
-wymiarowym, ![]() -mierzalnym wektorem losowym
takim, że
-mierzalnym wektorem losowym
takim, że ![]() dla
dla ![]() ,
,
![]() są funkcjami
lipschitzowskimi oraz
są funkcjami
lipschitzowskimi oraz ![]() jest
jest ![]() -wymiarowym procesem Wienera.
Wówczas równanie
-wymiarowym procesem Wienera.
Wówczas równanie
ma dokładnie jedno rozwiązanie ![]() . Ponadto
. Ponadto
14.4. Generator procesu dyfuzji.
W tej części zakładamy, że ![]() są funkcjami ciągłymi, zaś
są funkcjami ciągłymi, zaś ![]() jest
jest ![]() -wymiarowym procesem Wienera.
-wymiarowym procesem Wienera.
Definicja 14.6
Generatorem![]() -wymiarowego procesu dyfuzji spełniającego stochastyczne równanie różniczkowe
-wymiarowego procesu dyfuzji spełniającego stochastyczne równanie różniczkowe
nazywamy operator różniczkowy drugiego rzędu dany wzorem
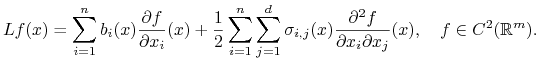 |
Definicja ta jest motywowana przez poniższy prosty, ale bardzo ważny fakt.
Stwierdzenie 14.2
Załóżmy, że ![]() jest generatorem procesu dyfuzji spełniającego równanie
jest generatorem procesu dyfuzji spełniającego równanie
![]() . Wówczas dla dowolnej funkcji
. Wówczas dla dowolnej funkcji ![]() takiej, że
takiej, że
![]() jest całkowalne, proces
jest całkowalne, proces
![]() jest ciągłym martyngałem lokalnym. Ponadto, jeśli
jest ciągłym martyngałem lokalnym. Ponadto, jeśli ![]() ma dodatkowo nośnik zwarty, to
ma dodatkowo nośnik zwarty, to ![]() jest martyngałem.
jest martyngałem.
Ze wzoru Itô łatwo sprawdzić, że
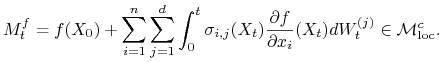 |
Jeśli ![]() , to funkcje
, to funkcje
![]() są ciągłe i mają nośnik zwarty w
są ciągłe i mają nośnik zwarty w
![]() , więc są ograniczone, zatem procesy
, więc są ograniczone, zatem procesy
![]() należą do
należą do ![]() dla dowolnego
dla dowolnego
![]() , więc
, więc ![]() jest martyngałem (a nawet martyngałem całkowalnym z kwadratem).
jest martyngałem (a nawet martyngałem całkowalnym z kwadratem).
Uwaga 14.3
Założenie o zwartym nośniku ![]() można w wielu przykładach istotnie osłabić. Załóżmy, że
współczynniki
można w wielu przykładach istotnie osłabić. Załóżmy, że
współczynniki ![]() i
i ![]() są lipschitzowskie oraz
są lipschitzowskie oraz ![]() . Wówczas, jak wiemy,
. Wówczas, jak wiemy,
![]() jest całkowalny z kwadratem oraz
jest całkowalny z kwadratem oraz ![]() dla
dla ![]() .
Stąd nietrudno
sprawdzić (używając lipschitzowskości
.
Stąd nietrudno
sprawdzić (używając lipschitzowskości ![]() ), że jeśli pochodne
), że jeśli pochodne ![]() są ograniczone, to
są ograniczone, to
![]() dla
dla ![]() , zatem
, zatem
![]() jest martyngałem.
jest martyngałem.
Przykład 14.5
Generatorem ![]() -wymiarowego procesu Wienera jest operator
-wymiarowego procesu Wienera jest operator
![]() .
.
Jeśli ![]() spełnia
spełnia
(![]() -wymiarowy proces Ornsteina-Uhlenbecka), to
-wymiarowy proces Ornsteina-Uhlenbecka), to
![]() .
.
Wykład zakończymy przykładem pokazującym związek między stochastycznymi równaniami różniczkowymi a równaniami cząstkowymi. Dokładna analiza takich związków jest ważną dziedziną łączącą rozumowania analityczne i probabilistyczne. Nieco więcej na ten temat można się będzie dowiedzieć na przedmiocie Procesy Stochastyczne.
Przykład 14.6
Dla ![]() niech
niech ![]() będzie rozwiązaniem równania stochastycznego
będzie rozwiązaniem równania stochastycznego
zaś ![]() odpowiadającym mu generatorem. Załóżmy, że
odpowiadającym mu generatorem. Załóżmy, że ![]() jest obszarem ograniczonym
oraz
jest obszarem ograniczonym
oraz ![]() spełnia równanie cząstkowe
spełnia równanie cząstkowe
Załóżmy dodatkowo, że ![]() daje się rozszerzyć do funkcji klasy
daje się rozszerzyć do funkcji klasy ![]() na pewnym otoczeniu
na pewnym otoczeniu
![]() . Wówczas
. Wówczas ![]() się rozszerza też do funkcji klasy
się rozszerza też do funkcji klasy ![]() .
Wybierzmy
.
Wybierzmy ![]() i określmy
i określmy
Wiemy, że proces ![]() jest martyngałem, zatem martyngałem jest
również
jest martyngałem, zatem martyngałem jest
również ![]() , ale
, ale
w szczegóności
Jeśli dodatkowo ![]() p.n. (to założenie jest spełnione np. dla procesu Wienera), to
z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej
p.n. (to założenie jest spełnione np. dla procesu Wienera), to
z twierdzenia Lebesgue'a o zbieżności zmajoryzowanej
Otrzynaliśmy więc stochastyczną reprezentację rozwiązania eliptycznego równania cząstkowego.
Podobne rozumowanie pokazuje, że (przy pewnych dodatkowych założeniach) rozwiązanie równania
ma postać zadaną wzorem Feynmana-Kaca
14.5. Zadania
Ćwiczenie 14.1
Zweryfikuj rachunki dla procesu Ornsteina-Uhlenbecka z Przykładu 14.2.
Ćwiczenie 14.2
i) Wykaż, że dla ![]() istnieje dokładnie jeden proces
istnieje dokładnie jeden proces ![]() taki, że
taki, że
Ponadto ![]() dla
dla ![]() .
.
ii) Oblicz ![]() .
.
iii) Znajdź stochastyczne równania różniczkowe spełnione przez ![]() i
i ![]() .
.
Ćwiczenie 14.3
Wykaż, że rozwiązanie równania ![]() eksploduje w skończonym
czasie.
eksploduje w skończonym
czasie.
Rozpatrz proces ![]() .
.
Ćwiczenie 14.4
Wykaż, że rozwiązanie równania
eksploduje w skończonym czasie. Ponadto wartość oczekiwana czasu do eksplozji jest skończona.
Ćwiczenie 14.5
Załóżmy, że ![]() jest ciągłą funkcją na
jest ciągłą funkcją na ![]() o wartościach w
macierzach
o wartościach w
macierzach ![]() ,
, ![]() jest ciągłą funkcją na
jest ciągłą funkcją na ![]() o wartościach w
macierzach
o wartościach w
macierzach ![]() , zaś
, zaś ![]() jest ciągłą funkcją na
jest ciągłą funkcją na ![]() o wartościach w
o wartościach w
![]() . Niech
. Niech ![]() będzie jedynym rozwiązaniem równania
będzie jedynym rozwiązaniem równania
Ponadto niech ![]() będzie
będzie ![]() -wymiarowym procesem Wienera, a
-wymiarowym procesem Wienera, a ![]() zmienną
losową niezależną od
zmienną
losową niezależną od ![]() . Wykaż, że
. Wykaż, że
jest rozwiązaniem równania deterministycznego
jest jedynym rozwiązaniem stochastycznego równania różniczkowego




