15. Twierdzenie Girsanowa
W czasie tego wykładu przyjmujemy jak zwykle, że ![]() jest ustaloną
przestrzenią probabilistyczną. Będziemy konstruowali inne miary probabilistyczne
na przestrzeni
jest ustaloną
przestrzenią probabilistyczną. Będziemy konstruowali inne miary probabilistyczne
na przestrzeni ![]() względem których proces Wienera z dryfem ma taki rozkład
jak zwykły proces Wienera.
Przez
względem których proces Wienera z dryfem ma taki rozkład
jak zwykły proces Wienera.
Przez ![]() będziemy rozumieli zawsze wartość oczekiwaną względem
będziemy rozumieli zawsze wartość oczekiwaną względem
![]() , wartość oczekiwaną
, wartość oczekiwaną ![]() względem innej miary
względem innej miary ![]() będziemy oznaczać
będziemy oznaczać ![]() .
Zauważmy, że jeśli
.
Zauważmy, że jeśli ![]() , tzn.
, tzn. ![]() , to
, to
15.1. Przypadek dyskretny
Załóżmy, że zmienne ![]() są niezależne i mają standardowy rozkład normalny
są niezależne i mają standardowy rozkład normalny
![]() . Wprowadźmy nową miarę
. Wprowadźmy nową miarę ![]() na
na ![]() wzorem
wzorem
![]() , tzn.
, tzn.
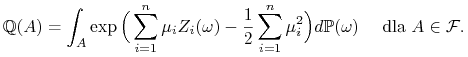 |
Zauważmy, że
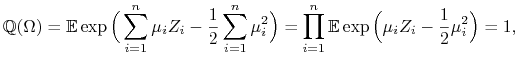 |
więc ![]() jest miarą probabilistyczną na
jest miarą probabilistyczną na ![]() . Ponadto dla
dowolnego zbioru
. Ponadto dla
dowolnego zbioru ![]() ,
,
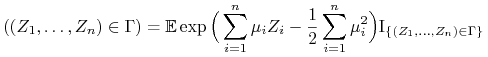 |
|||
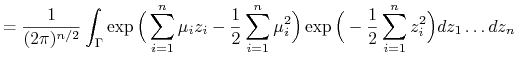 |
|||
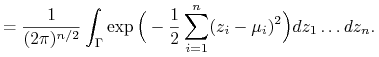 |
Zatem względem miary ![]() zmienne
zmienne ![]() są niezależne oraz mają rozkład
są niezależne oraz mają rozkład
![]() .
.
Definiując ![]() widzimy, że względem
widzimy, że względem ![]() zmienne
zmienne
![]() są sumami niezależnych standardowych zmiennych normalnych (czyli mają ten sam rozkład co
są sumami niezależnych standardowych zmiennych normalnych (czyli mają ten sam rozkład co
![]() względem
względem ![]() ). Podczas dalszej części wykładu pokażemy, że
można podobny fakt sformułować w przypadku ciągłym, gdy
). Podczas dalszej części wykładu pokażemy, że
można podobny fakt sformułować w przypadku ciągłym, gdy ![]() zastąpimy procesem Wienera,
a sumy
zastąpimy procesem Wienera,
a sumy ![]() całką
całką ![]() .
.
15.2. Twierdzenie Girsanowa dla procesu Wienera
Załóżmy, że ![]() , proces
, proces ![]() jest prognozowalny oraz
jest prognozowalny oraz ![]() p.n.,
wówczas
p.n.,
wówczas ![]() , proces
, proces ![]() jest martyngałem
lokalnym na
jest martyngałem
lokalnym na ![]() oraz
oraz ![]() . Co więcej można też określić wartość
. Co więcej można też określić wartość
![]() i
i ![]() w punkcie
w punkcie ![]() .
Zatem jak wiemy (zob. Stwierdzenie 14.1) proces
.
Zatem jak wiemy (zob. Stwierdzenie 14.1) proces
jest martyngałem lokalnym na ![]() .
.
Lemat 15.1
Jeśli ![]() jest ciągłym martyngałem lokalnym na
jest ciągłym martyngałem lokalnym na ![]() , to proces
, to proces
![]() jest martyngałem na przedziale skończonym
jest martyngałem na przedziale skończonym ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy ![]() .
.
Implikacja ”![]() ” jest oczywista, bo
” jest oczywista, bo ![]() . Wystarczy więc udowodnić
”
. Wystarczy więc udowodnić
”![]() ”.
”.
Wiemy, że ![]() jest nieujemnym martyngałem lokalnym, zatem jest nadmartyngałem
(Stwierdzenie 9.6). Ustalmy
jest nieujemnym martyngałem lokalnym, zatem jest nadmartyngałem
(Stwierdzenie 9.6). Ustalmy ![]() ,
wówczas
,
wówczas ![]() p.n..
Ponadto
p.n..
Ponadto ![]() , czyli, jeśli
, czyli, jeśli
![]() , to
, to ![]() i
i
a więc ![]() p.n..
p.n..
Twierdzenie 15.1
Załóżmy, że ![]() , proces
, proces ![]() jest prognozowalny oraz
jest prognozowalny oraz
![]() p.n.. Niech
p.n.. Niech ![]() ,
wówczas, jeśli
,
wówczas, jeśli ![]() (czyli
(czyli ![]() jest martyngałem na
jest martyngałem na ![]() ), to proces
), to proces
jest procesem Wienera na zmodyfikowanej przestrzeni
propabilistycznej
![]() , gdzie
, gdzie ![]() , tzn.
, tzn.
Zmienna ![]() jest nieujemna i
jest nieujemna i ![]() , więc
, więc ![]() jest miarą
probabilistyczną.
Zauważmy też, że jeśli
jest miarą
probabilistyczną.
Zauważmy też, że jeśli ![]() , to
, to ![]() , czyli zdarzenia,
które zachodzą
, czyli zdarzenia,
które zachodzą ![]() prawie
na pewno, zachodzą też
prawie
na pewno, zachodzą też ![]() prawie na pewno.
Proces
prawie na pewno.
Proces
![]() jest ciągły, adaptowalny względem
jest ciągły, adaptowalny względem ![]() oraz
oraz ![]() .
Wystarczy zatem, na mocy Twierdzenia 13.5 wykazać, że
dla
.
Wystarczy zatem, na mocy Twierdzenia 13.5 wykazać, że
dla ![]() , proces
, proces ![]() jest
martyngałem lokalnym względem
jest
martyngałem lokalnym względem ![]() . Zauważmy, że
. Zauważmy, że
gdzie ![]() . Zatem proces
. Zatem proces ![]() jest martyngałem
lokalnym
względem
jest martyngałem
lokalnym
względem ![]() , czyli istnieją
, czyli istnieją ![]() takie, że
takie, że ![]() jest
martyngałem. Ustalmy
jest
martyngałem. Ustalmy ![]() , wtedy dla dowolnego ograniczonego momentu zatrzymania
, wtedy dla dowolnego ograniczonego momentu zatrzymania ![]() ,
,
zatem z twierdzenia odwrotnego do twierdzenia Dooba wynika, że ![]() jest
martyngałem względem
jest
martyngałem względem ![]() , czyli
, czyli ![]() jest
jest ![]() -martyngałem lokalnym.
-martyngałem lokalnym.
W pewnych zastosowaniach wygodnie jest mieć miarę względem której proces ![]() jest
procesem Wienera na całej półprostej
jest
procesem Wienera na całej półprostej ![]() .
.
Twierdzenie 15.2
Załóżmy, że ![]() , zaś proces
, zaś proces ![]() i miary
i miary ![]() dla
dla ![]() są określone jak
poprzednio. Wówczas, jeśli
są określone jak
poprzednio. Wówczas, jeśli ![]() dla wszystkich
dla wszystkich ![]() (czyli
(czyli ![]() jest martyngałem
na
jest martyngałem
na ![]() ), to istnieje dokładnie jedna miara probabilistyczna
), to istnieje dokładnie jedna miara probabilistyczna ![]() na
na
![]() taka, że
taka, że ![]() dla
dla ![]() i
i ![]() . Proces
. Proces ![]() jest względem
jest względem ![]() procesem Wienera na
procesem Wienera na ![]() .
.
Szkic Dowodu.
Na zbiorach postaci ![]() ,
,
![]() ,
, ![]() kładziemy
kładziemy
![]() . Otrzymujemy w ten sposób zgodną rodzinę miar
probabilistycznych, która na
mocy twierdzenia Kołmogorowa przedłuża się w spośób jednoznaczny do miary
. Otrzymujemy w ten sposób zgodną rodzinę miar
probabilistycznych, która na
mocy twierdzenia Kołmogorowa przedłuża się w spośób jednoznaczny do miary ![]() na
na
![]() .
.
Uwaga 15.1
O ile miara ![]() jest absolutnie ciągła względem
jest absolutnie ciągła względem ![]() (tzn.
(tzn. ![]() , jeśli
, jeśli ![]() ),
to miara
),
to miara ![]() zadana przez ostatnie twierdzenie taka być nie musi. Istotnie
określmy
zadana przez ostatnie twierdzenie taka być nie musi. Istotnie
określmy ![]() , czyli
, czyli ![]() . Niech
. Niech
Wówczas z mocnego prawa wielkich liczb dla proceseu Wienera ![]() oraz
oraz
![]() ,
z drugiej strony
,
z drugiej strony ![]() , zatem miary
, zatem miary ![]() i
i ![]() są wzajemnie
singularne na
są wzajemnie
singularne na
![]() , mimo, że po odbcięciu do
, mimo, że po odbcięciu do ![]() dla
dla ![]() są
względem siebie absolutnie ciągłe. Można pokazać, że albsolutna ciągłość
są
względem siebie absolutnie ciągłe. Można pokazać, że albsolutna ciągłość ![]() względem
względem ![]() wiąże się
z jednostajną całkowalnością martyngału
wiąże się
z jednostajną całkowalnością martyngału ![]() .
.
Naturalne jest pytanie kiedy spełnione są założenia twierdzenia Girsanowa, czyli kiedy
![]() jest martyngałem. Użyteczne jest następujące kryterium.
jest martyngałem. Użyteczne jest następujące kryterium.
Twierdzenie 15.3 (Kryterium Nowikowa)
Jeśli ![]() jest procesem prognozowalnym spełniającym warunek
jest procesem prognozowalnym spełniającym warunek
![]() , to
spełnione są założenia twierdzenia Girsanowa, tzn. proces
, to
spełnione są założenia twierdzenia Girsanowa, tzn. proces
![]() jest martyngałem na
jest martyngałem na ![]() .
.
Kryterium Nowikowa jest konsekwencją silniejszego twierdzenia, które przedstawimy bez dowodu.
Twierdzenie 15.4
Załóżmy, że ![]() jest ciągłym martyngałem lokalnym takim, że dla wszystkich
jest ciągłym martyngałem lokalnym takim, że dla wszystkich ![]() ,
,
![]() . Niech
. Niech
![]() ,
wówczas
,
wówczas ![]() dla wszystkich
dla wszystkich ![]() , czyli
, czyli ![]() jest martyngałem.
jest martyngałem.
Twierdzenie Girsanowa można sformułować też w przypadku wielowymiarowym.
Twierdzenie 15.5
Załóżmy, że ![]() proces
proces ![]() -wymiarowy taki, że
-wymiarowy taki, że ![]() oraz
oraz ![]() . Niech
. Niech ![]() będzie
będzie ![]() -wymiarowym procesem Wienera oraz
-wymiarowym procesem Wienera oraz
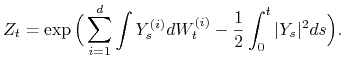 |
Wówczas, jeśli ![]() (czyli
(czyli ![]() jest martyngałem na
jest martyngałem na ![]() ), to proces
), to proces
jest procesem Wienera na ![]() względem miary probabilistycznej
względem miary probabilistycznej ![]() takiej, że
takiej, że
![]() .
.
Kryterium Nowikowa w przypadku ![]() -wymiarowym ma postać
-wymiarowym ma postać
Twierdzenie 15.6
Jeśli ![]() jest
jest ![]() -wymiarowym procesem prognozowalnym spełniającym warunek
-wymiarowym procesem prognozowalnym spełniającym warunek
![]() , to
spełnione są założenia twierdzenia Girsanowa.
, to
spełnione są założenia twierdzenia Girsanowa.
15.3. Zadania
Ćwiczenie 15.1
Znajdź taką miarę probabilistyczną ![]() na
na ![]() , by proces
, by proces
![]() był procesem Wienera
względem
był procesem Wienera
względem ![]() .
.
Ćwiczenie 15.2
Niech ![]() ,
, ![]() będzie procesem Wienera na
będzie procesem Wienera na ![]() ,
,
Stosując twierdzenie Girsanowa wykaż,
że jeśli ![]() , to istnieje miara probabilistyczna
, to istnieje miara probabilistyczna ![]() taka, że
na przestrzeni probabilistycznej
taka, że
na przestrzeni probabilistycznej ![]() ,
,
![]() jest procesem Wienera oraz
jest procesem Wienera oraz
Ćwiczenie 15.3
Niech ![]() oznacza miarę Wienera na
oznacza miarę Wienera na ![]() (tzn. rozkład wyznaczony
przez proces Wienera na
(tzn. rozkład wyznaczony
przez proces Wienera na ![]() ). Dla
). Dla ![]() określamy nową miarę
określamy nową miarę
![]() wzorem
wzorem ![]() . Wykaż, że
. Wykaż, że
a) jeśli ![]() dla
dla ![]() oraz
oraz
![]() , to miara
, to miara ![]() jest absolutnie ciągła względem
jest absolutnie ciągła względem ![]() oraz znajdź jej gęstość,
oraz znajdź jej gęstość,
b*) jeśli ![]() nie ma powyższej postaci, to miary
nie ma powyższej postaci, to miary ![]() i
i ![]() są wzajemnie
singularne.
są wzajemnie
singularne.




