Zagadnienia

5.1 Definicje i przykłady
5.2 Nierówności maksymalne
5.3 Zadania

5. Martyngały z czasem ciągłym

Tak jak podczas poprzedniego wykładu, jeśli nie zaznaczymy inaczej, będziemy zakładać, że $T$ jest lewostronnie domkniętym przedziałem.

5.1. Definicje i przykłady

Definicja 5.1

Mówimy, że $(X_{{t}})_{{t\in T}}$ jest martyngałem (odp. podmartyngałem, nadmartyngałem) względem filtracji $({\mathcal{F}}_{{t}})_{{t\in T}}$ lub, że $(X_{{t}},{\mathcal{F}}_{{t}})_{{t\in T}}$ jest martyngałem (odp. podmartyngałem, nadmartyngałem), jeśli
a) dla wszystkich $t\in T$ , $X_{{t}}$ jest ${\mathcal{F}}_{{t}}$ -mierzalny i ${\mathbb{E}}|X_{{t}}|<\infty$ ,
b) dla dowolnych $s,t\in T,s<t$ , ${\mathbb{E}}(X_{{t}}|{\mathcal{F}}_{{s}})=X_{{s}}$ p.n. (odp. $\geq$ dla podmartyngału i $\leq$ dla nadmartyngału).

Przykład 5.1

Jeśli $X$ jest całkowalną zmienną losową, a ${\mathcal{F}}_{{t}}$ dowolną filtracją to $X_{{t}}:={\mathbb{E}}(X|{\mathcal{F}}_{{t}})$ jest martyngałem.
Sprawdzamy dla $t>s$ ,

${\mathbb{E}}(X_{{t}}|{\mathcal{F}}_{{s}})={\mathbb{E}}({\mathbb{E}}(X|{\mathcal{F}}_{{t}})|{\mathcal{F}}_{{s}})={\mathbb{E}}(X|{\mathcal{F}}_{{s}})=X_{s}\quad\mbox{ p.n.}.$

Przykład 5.2

$(W_{{t}})_{{t\geq 0}}$ jest martyngałem względem naturalnej filtracji ${\mathcal{F}}_{{t}}=\sigma(W_{{s}}\colon s\leq t)$ .
Istotnie dla $t>s$ mamy z niezależności przyrostów

${\mathbb{E}}(W_{{t}}|{\mathcal{F}}_{{s}})={\mathbb{E}}(W_{{s}}|{\mathcal{F}}_{{s}})+{\mathbb{E}}(W_{{t}}-W_{{s}}|{\mathcal{F}}_{{s}})=W_{{s}}+{\mathbb{E}}(W_{{t}}-W_{{s}})=W_{{s}}\quad\mbox{ p.n.}.$

Przykład 5.3

$(W_{{t}}^{{2}})_{{t\geq 0}}$ jest podmartyngałem, a $(W_{{t}}^{{2}}-t)_{{t\geq 0}}$ martyngałem względem naturalnej filtracji ${\mathcal{F}}_{{t}}=\sigma(W_{{s}}\colon s\leq t)$ .
Liczymy dla $t>s$ ,

	$\displaystyle{\mathbb{E}}(W_{{t}}^{{2}}\|{\mathcal{F}}_{{s}})$	$\displaystyle={\mathbb{E}}(W_{{s}}^{{2}}\|{\mathcal{F}}_{{s}})+{\mathbb{E}}(2W_{{s}}(W_{{t}}-W_{{s}})\|{\mathcal{F}}_{{s}})+{\mathbb{E}}((W_{{t}}-W_{{s}})^{{2}}\|{\mathcal{F}}_{{s}})$
		$\displaystyle=W_{{s}}^{{2}}+2W_{{s}}{\mathbb{E}}(W_{{t}}-W_{{s}})+{\mathbb{E}}(W_{{t}}-W_{{s}})^{{2}}=W_{{s}}^{{2}}+t-s\quad\mbox{ p.n.}.$

Uwaga 5.1

W ostatnich dwu przykładach filtrację $({\mathcal{F}}_{t}^{W})$ można zastąpić filtracją $({\mathcal{F}}_{{t+}}^{W})$ .

Stwierdzenie 5.1

Załóżmy, że $(X_{{t}},{\mathcal{F}}_{{t}})$ jest martyngałem (odp. podmartyngałem), zaś $f\colon{\mathbb{R}}\rightarrow{\mathbb{R}}$ funkcją wypukłą (odp. wypukłą i niemalejącą) taką, że ${\mathbb{E}}|f(X_{{t}})|<\infty$ dla wszystkich $t$ . Wówczas $(f(X_{{t}}),{\mathcal{F}}_{{t}})$ jest podmartyngałem.

Z nierówności Jensena mamy ${\mathbb{E}}(f(X_{{t}})|{\mathcal{F}}_{{s}})\geq f({\mathbb{E}}(X_{{t}}|{\mathcal{F}}_{{s}}))$ p.n., a ostatnia zmienna jest równa $f(X_{{s}})$ w przypadku martyngału i nie mniejsza niż $f(X_{{s}})$ dla podmartyngału.

∎

Przypomnijmy definicję funkcji harmonicznych.

Definicja 5.2

Funkcję $f\colon{\mathbb{R}}^{{n}}\rightarrow{\mathbb{R}}$ nazywamy podharmoniczną (odp. harmoniczną, nadharmoniczną) jeśli jest ograniczona na zbiorach zwartych oraz

$\forall _{{x\in{\mathbb{R}}^{{n}}}}\ \forall _{{r\geq 0}}\ f(x)\leq\frac{1}{|S^{{n-1}}|}\int _{{S^{{n-1}}}}f(x+ry)d\sigma(y)\quad\mbox{(odp.\ $=$, $\geq$)},$

gdzie $\sigma(y)$ jest miarą powierzchniową na sferze, a $|S_{{n-1}}|=\int _{{S^{{n-1}}}}d\sigma(y)=2\pi^{{n/2}}(\Gamma(n/2))^{{-1}}$ .

Uwaga 5.2

Funkcja gładka jest harmoniczna (odp. pod-,nad-) wtedy i tylko wtedy, gdy $\Delta f=0$ (odp. $\geq$ , $\leq$ ). Dla $n=1$ warunek podharmoniczności jest równoważny wypukłości. Funkcja $f(x)=-\ln|x-x_{{0}}|$ jest nadharmoniczna na ${\mathbb{R}}^{{2}}$ , a funkcja $f(x)=|x-x_{{0}}|^{{2-d}}$ nadharmoniczna na ${\mathbb{R}}^{{d}}$ dla $d>2$ .

Stwierdzenie 5.2

Niech $W_{{t}}=(W_{{t}}^{{(1)}},\ldots,W_{{t}}^{{(d)}})$ będzie $d$ -wymiarowym procesem Wienera, ${\mathcal{F}}_{{t}}^{{W}}=\sigma(W_{{s}}\colon s\leq t)$ , zaś $f\colon{\mathbb{R}}^{{d}}\rightarrow{\mathbb{R}}$ funkcją harmoniczną (odp. nad-, pod-) taką, że ${\mathbb{E}}|f(W_{{t}})|<\infty$ dla $t\geq 0$ . Wówczas $(f(W_{{t}}),{\mathcal{F}}_{{t}}^{{W}})$ jest martyngałem (odp. nad-, pod-).

Liczymy dla $t>s$ korzystając z niezależności przyrostów procesu Wienera oraz wprowadzając współrzędne sferyczne,

	$\displaystyle{\mathbb{E}}(f(W_{{t}})\|{\mathcal{F}}_{{s}}^{W})$	$\displaystyle={\mathbb{E}}(f(W_{{s}}+(W_{{t}}-W_{{s}}))\|{\mathcal{F}}_{{s}}^{W})$
		$\displaystyle=(2\pi(t-s))^{{-d/2}}\int _{{{\mathbb{R}}^{{d}}}}f(W_{{s}}+x)e^{{-\frac{\|x\|^{{2}}}{2(t-s)}}}dx$
		$\displaystyle=(2\pi(t-s))^{{-d/2}}\int _{{0}}^{{\infty}}r^{{d-1}}e^{{-\frac{r^{{2}}}{2(t-s)}}}\Big(\int _{{S^{{d-1}}}}f(W_{{s}}+y)d\sigma(y)\Big)dr$
		$\displaystyle=(2\pi(t-s))^{{-d/2}}\|S^{{d-1}}\|f(W_{{s}})\int _{{0}}^{{\infty}}r^{{d-1}}e^{{-\frac{r^{{2}}}{2(t-s)}}}dr$
		$\displaystyle=(2\pi)^{{-d/2}}\|S^{{d-1}}\|\int _{{0}}^{{\infty}}r^{{d-1}}e^{{-\frac{r^{{2}}}{2}}}drf(W_{{s}})=c_{{d}}f(W_{{s}})\quad\mbox{ p.n.}.$

By zauważyć, że $c_{{d}}=1$ przeprowadzamy albo bezpośredni rachunek, albo podstawiamy powyżej $f\equiv 1$ .

∎

5.2. Nierówności maksymalne

Zacznijmy od przypomnienia podstawowego lematu dla martyngałów z czasem dyskretnym, pochodzącego od Dooba.

Lemat 5.1

Załóżmy, że $(X_{{n}},{\mathcal{F}}_{{n}})_{{0\leq n\leq N}}$ jest martyngałem (odp. nad-, pod-), zaś $0\leq\tau\leq\sigma\leq N$ dwoma momentami zatrzymania. Wówczas

${\mathbb{E}}(X_{{\sigma}}|{\mathcal{F}}_{{\tau}})=X_{{\tau}}\quad\mbox{ p.n. (odp. $\leq$, $\geq$).}$

Musimy pokazać, że dla $A\in{\mathcal{F}}_{{\tau}}$ , ${\mathbb{E}}X_{{\tau}}{\mathrm{I}}_{{A}}={\mathbb{E}}X_{{\sigma}}{\mathrm{I}}_{{A}}$ . Połóżmy $A_{{k}}:=A\cap\{\tau=k\}$ dla $k=0,1,\ldots,N$ . Mamy

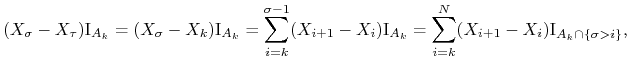$(X_{{\sigma}}-X_{{\tau}}){\mathrm{I}}_{{A_{{k}}}}=(X_{{\sigma}}-X_{{k}}){\mathrm{I}}_{{A_{{k}}}}=\sum _{{i=k}}^{{\sigma-1}}(X_{{i+1}}-X_{{i}}){\mathrm{I}}_{{A_{{k}}}}=\sum _{{i=k}}^{{N}}(X_{{i+1}}-X_{{i}}){\mathrm{I}}_{{A_{{k}}\cap\{\sigma>i\}}},$

zatem

${\mathbb{E}}[(X_{{\sigma}}-X_{{\tau}}){\mathrm{I}}_{{A_{{k}}}}]=\sum _{{i=k}}^{{N}}{\mathbb{E}}[(X_{{i+1}}-X_{{i}}){\mathrm{I}}_{{A_{{k}}\cap\{\sigma>i\}}}]=0,$

gdyż $A_{{k}}\cap\{\sigma>i\}\in{\mathcal{F}}_{{i}}$ . Stąd

${\mathbb{E}}[(X_{{\sigma}}-X_{{\tau}}){\mathrm{I}}_{{A}}]=\sum _{{k=0}}^{{N}}{\mathbb{E}}[(X_{{\sigma}}-X_{{\tau}}){\mathrm{I}}_{{A_{{k}}}}]=0.$

∎

Uwaga 5.3

Lemat 5.1 nie jest prawdziwy, jeśli nie założymy ograniczoności momentów zatrzymania, np. biorąc $X_{{n}}=\sum _{{k=1}}^{{n}}\varepsilon _{{n}}$ , gdzie $\varepsilon _{{n}}$ niezależne zmienne losowe takie, że ${\mathbb{P}}(\varepsilon _{{n}}=\pm 1)=1/2$ , ${\mathcal{F}}_{{n}}=\sigma(\varepsilon _{{1}},\ldots,\varepsilon _{{n}})$ , $\tau=0$ , $\sigma=\inf\{ n\colon X_{{n}}=1\}$ widzimy, że ${\mathbb{E}}X_{{\tau}}=0\neq 1={\mathbb{E}}X_{{\sigma}}$ .

Przed sformułowaniem kolejnego lematu przypomnijmy, że przez $X^{+}$ i $X^{-}$ oznaczamy odpowiednio część dodatnią i ujemną zmiennej $X$ , tzn. $X^{{+}}:=\max{X,0}$ oraz $X^{{-}}:=\max{-X,0}$ .

Lemat 5.2

Niech $(X_{{n}},{\mathcal{F}}_{{n}})_{{0\leq n\leq N}}$ będzie podmartyngałem, wówczas dla wszystkich $\lambda\geq 0$ mamy

$\mathrm{a)}\ \ \lambda{\mathbb{P}}\Big(\max _{{0\leq n\leq N}}X_{{n}}\geq\lambda\Big)\leq{\mathbb{E}}X_{{N}}{\mathrm{I}}_{{\{\max _{{0\leq n\leq N}}X_{{n}}\geq\lambda\}}}\leq{\mathbb{E}}X_{{N}}^{{+}},\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$

$\mathrm{b)}\ \ \lambda{\mathbb{P}}\Big(\min _{{0\leq n\leq N}}X_{{n}}\leq-\lambda\Big)\leq{\mathbb{E}}X_{{N}}{\mathrm{I}}_{{\{\min _{{0\leq n\leq N}}X_{{n}}>-\lambda\}}}-{\mathbb{E}}X_{{0}}\leq{\mathbb{E}}X_{{N}}^{{+}}-{\mathbb{E}}X_{{0}}.\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$

a) Niech $\tau:=\inf\{ n\colon X_{{n}}\geq\lambda\}$ , z Lematu 5.1 dostajemy (wobec $\tau\wedge N\leq N$ )

	$\displaystyle{\mathbb{E}}X_{{N}}$	$\displaystyle\geq{\mathbb{E}}X_{{\tau\wedge N}}={\mathbb{E}}X_{{\tau}}{\mathrm{I}}_{{\{\max _{{0\leq n\leq N}}X_{{n}}\geq\lambda\}}}+{\mathbb{E}}X_{{N}}{\mathrm{I}}_{{\{\max _{{0\leq n\leq N}}X_{{n}}<\lambda\}}}$
		$\displaystyle\geq\lambda{\mathbb{P}}(\max _{{0\leq n\leq N}}X_{{n}}\geq\lambda)+{\mathbb{E}}X_{{N}}{\mathrm{I}}_{{\{\max _{{0\leq n\leq N}}X_{{n}}<\lambda\}}}$

i po przeniesieniu wartości oczekiwanych na jedną stronę dostajemy postulowaną nierówność.

b) Definiujemy $\tau:=\inf\{ n\colon X_{{n}}\leq-\lambda\}$ , z Lematu 5.1 dostajemy (wobec $\tau\wedge N\geq 0$ )

	$\displaystyle{\mathbb{E}}X_{{0}}$	$\displaystyle\leq{\mathbb{E}}X_{{\tau\wedge N}}={\mathbb{E}}X_{{\tau}}{\mathrm{I}}_{{\{\min _{{0\leq n\leq N}}X_{{n}}\leq-\lambda\}}}+{\mathbb{E}}X_{{N}}{\mathrm{I}}_{{\{\min _{{0\leq n\leq N}}X_{{n}}>-\lambda\}}}$
		$\displaystyle\leq-\lambda{\mathbb{P}}(\min _{{0\leq n\leq N}}X_{{n}}\leq-\lambda)+{\mathbb{E}}X_{{N}}{\mathrm{I}}_{{\{\min _{{0\leq n\leq N}}X_{{n}}>-\lambda\}}}$

i znów wystarczy pogrupować wartości oczekiwane.

∎

Wniosek 5.1

Jeśli $(X_{{n}},{\mathcal{F}}_{{n}})_{{0\leq n\leq N}}$ jest martyngałem, bądź nieujemnym podmartyngałem, to

$\mathrm{a)}\ \ \forall _{{p\geq 1}}\ \forall _{{\lambda\geq 0}}\ \lambda^{{p}}{\mathbb{P}}\Big(\max _{{0\leq n\leq N}}|X_{{n}}|\geq\lambda\Big)\leq{\mathbb{E}}|X_{{N}}|^{{p}},\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$

$\mathrm{b)}\ \ \forall _{{p>1}}\ {\mathbb{E}}|X_{{N}}|^{{p}}\leq{\mathbb{E}}\max _{{0\leq n\leq N}}|X_{{n}}|^{{p}}\leq\Big(\frac{p}{p-1}\Big)^{{p}}{\mathbb{E}}|X_{{N}}|^{{p}}.\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$

a) Funkcja $f(t)=|t|^{{p}}$ jest wypukła, niemalejąca na ${\mathbb{R}}_{{+}}$ , stąd na mocy Stwierdzenia 5.1 $|X_{{n}}|^{{p}}$ jest nieujemnym podmartyngałem, zatem z Lematu 5.2 mamy

	$\displaystyle\lambda^{{p}}{\mathbb{P}}\Big(\max _{{0\leq n\leq N}}\|X_{{n}}\|\geq\lambda\Big)$	$\displaystyle=\lambda^{{p}}{\mathbb{P}}\Big(\max _{{0\leq n\leq N}}\|X_{{n}}\|^{p}\geq\lambda^{p}\Big)$
		$\displaystyle\leq{\mathbb{E}}\|X_{{N}}\|^{{p}}{\mathrm{I}}_{{\{\max _{{0\leq n\leq N}}\|X_{{n}}\|^{{p}}\geq\lambda^{{p}}\}}}\leq{\mathbb{E}}\|X_{{N}}\|^{{p}}.$

b) Niech $X^{{*}}:=\max _{{0\leq n\leq N}}|X_{{n}}|$ , z rachunku przeprowadzonego powyżej dla $p=1$ ,

$\lambda{\mathbb{P}}(X^{{*}}\geq\lambda)\leq{\mathbb{E}}|X_{{N}}|{\mathrm{I}}_{{\{ X^{{*}}\geq\lambda\}}}.$

Stosując kolejno wzór na całkowanie przez części, twierdzenie Fubiniego i nierówność Höldera dostajemy

	$\displaystyle{\mathbb{E}}\max _{{0\leq n\leq N}}\|X_{{n}}\|^{{p}}$	$\displaystyle=p\int _{{0}}^{{\infty}}\lambda^{{p-1}}{\mathbb{P}}(X^{{}}\geq\lambda)d\lambda\leq p\int _{{0}}^{{\infty}}\lambda^{{p-2}}{\mathbb{E}}\|X_{{N}}\|{\mathrm{I}}_{{\{ X^{{}}\geq\lambda\}}}d\lambda$
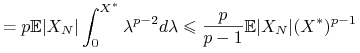		$\displaystyle=p{\mathbb{E}}\|X_{{N}}\|\int _{{0}}^{{X^{{}}}}\lambda^{{p-2}}d\lambda\leq\frac{p}{p-1}{\mathbb{E}}\|X_{{N}}\|(X^{{}})^{{p-1}}$
		$\displaystyle\leq\frac{p}{p-1}({\mathbb{E}}\|X_{{N}}\|^{{p}})^{{1/p}}({\mathbb{E}}(X^{{*}})^{{p}})^{{(p-1)/p}}.$

Jeśli ${\mathbb{E}}|X_{{N}}|^{{p}}<\infty$ , to na mocy nierówności Jensena, ${\mathbb{E}}|X_{{n}}|^{{p}}\leq{\mathbb{E}}|X_{{N}}|^{{p}}<\infty$ dla $0\leq n\leq N$ oraz ${\mathbb{E}}(X^{{*}})^{{p}}\leq{\mathbb{E}}\sum _{{n=0}}^{{N}}|X_{{n}}|^{{p}}<\infty$ . Dzieląc więc otrzymaną poprzednio nierówność stronami przez $({\mathbb{E}}(X^{{*}})^{{p}})^{{(p-1)/p}}$ dostajemy

$({\mathbb{E}}(X^{{*}})^{{p}})^{{1/p}}\leq\frac{p}{p-1}({\mathbb{E}}|X_{{N}}|^{{p}})^{{1/p}}.$

∎

Udowodnimy teraz nierówność maksymalną Dooba w przypadku ciągłym.

Twierdzenie 5.1

Załóżmy, że $(X_{{t}},{\mathcal{F}}_{{t}})_{{t\in T}}$ martyngałem lub nieujemnym podmartyngałem, o prawostronnie ciągłych trajektoriach. Wówczas

$\mathrm{a)}\ \ \forall _{{p\geq 1}}\ \forall _{{\lambda\geq 0}}\ \lambda^{{p}}{\mathbb{P}}\Big(\sup _{{t\in T}}|X_{{t}}|\geq\lambda\Big)\leq\sup _{{t\in T}}{\mathbb{E}}|X_{{t}}|^{{p}},\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$

$\mathrm{b)}\ \ \forall _{{p>1}}\ \sup _{{t\in T}}{\mathbb{E}}|X_{{t}}|^{{p}}\leq{\mathbb{E}}\sup _{{t\in T}}|X_{{t}}|^{{p}}\leq\Big(\frac{p}{p-1}\Big)^{{p}}\sup _{{t\in T}}{\mathbb{E}}|X_{{t}}|^{{p}}.\phantom{aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa}$

Uwaga 5.4

Oczywiście, jeśli $T$ zawiera element maksymalny $t_{{{\rm max}}}$ , to przy założeniach twierdzenia $\sup _{{t\in T}}{\mathbb{E}}|X_{{t}}|^{{p}}={\mathbb{E}}|X_{{t_{{{\rm max}}}}}|^{{p}}$ .

Jeśli $D$ jest skończonym podzbiorem $T$ , to na podstawie Wniosku 5.1 dostajemy

$\lambda^{{p}}{\mathbb{P}}\Big(\sup _{{t\in D}}|X_{{t}}|\geq\lambda\Big)\leq\sup _{{t\in D}}{\mathbb{E}}|X_{{t}}|^{{p}}\leq\sup _{{t\in T}}{\mathbb{E}}|X_{{t}}|^{{p}}.$

Niech $T_{{0}}$ będzie gęstym podzbiorem $T$ zawierającym prawy koniec $T$ (o ile taki istnieje), zaś $D_{{n}}$ wstępującym ciągiem skończonych podzbiorów $T_{{0}}$ takim, że $\bigcup _{{n}}D_{{n}}=T_{{0}}$ . Wówczas dla dowolnego $\tilde{\lambda}>0$ dostajemy na mocy prawostronnej ciągłości

	$\displaystyle\tilde{\lambda}^{{p}}{\mathbb{P}}\Big(\sup _{{t\in T}}\|X_{{t}}\|>\tilde{\lambda}\Big)$	$\displaystyle=\tilde{\lambda}^{{p}}{\mathbb{P}}\Big(\sup _{{t\in T_{{0}}}}\|X_{{t}}\|>\tilde{\lambda}\Big)$
		$\displaystyle=\lim _{{n\rightarrow\infty}}\tilde{\lambda}^{{p}}{\mathbb{P}}\Big(\sup _{{t\in D_{{n}}}}\|X_{{t}}\|>\tilde{\lambda}\Big)\leq\sup _{{t\in T}}{\mathbb{E}}\|X_{{t}}\|^{{p}}.$

Biorąc ciąg $\tilde{\lambda}_{{n}}\nearrow\lambda$ dostajemy postulowaną w a) nierówność. Nierówność z punktu b) wynika z Wniosku 5.1 w podobny sposób.

∎

Uwaga 5.5

Punkt b) Twierdzenia 5.1 nie zachodzi dla $p=1$ – można skonstruować martyngał dla którego $\sup _{{t}}{\mathbb{E}}|X_{{t}}|<\infty$ , ale ${\mathbb{E}}\sup _{{t}}|X_{{t}}|=\infty$ . Zachodzi jednak (przy założeniach Twierdzenia 5.1) nierówność

${\mathbb{E}}\sup _{{t\in T}}|X_{{t}}|\leq\frac{e}{e-1}\Big(1+\sup _{{t\in T}}{\mathbb{E}}|X_{{t}}|\ln^{{+}}|X_{{t}}|\Big).$

Wniosek 5.2

Dla dowolnych $u,s>0$ zachodzi

$\ {\mathbb{P}}\Big(\sup _{{0\leq t\leq s}}W_{{t}}\geq u\Big)\leq e^{{-\frac{u^{{2}}}{2s}}}.$

Ustalmy $\lambda>0$ , wówczas $M_{{t}}:=\exp(\lambda W_{{t}}-\frac{\lambda^{{2}}t}{2})$ jest martyngałem względem filtracji ${\mathcal{F}}_{{t}}^{{W}}$ generowanej przez proces Wienera (Ćwiczenie 5.2). Stąd na mocy Twierdzenia 5.1 a) z $p=1$ i nieujemności $M_{{t}}$ dostajemy

	$\displaystyle{\mathbb{P}}\Big(\sup _{{0\leq t\leq s}}W_{{t}}\geq u\Big)$	$\displaystyle\leq{\mathbb{P}}\Big(\sup _{{0\leq t\leq s}}M_{{t}}\geq e^{{\lambda u-\frac{\lambda^{{2}}s}{2}}}\Big)$
		$\displaystyle\leq e^{{-\lambda u+\frac{\lambda^{{2}}s}{2}}}\sup _{{0\leq t\leq s}}{\mathbb{E}}\|M_{{t}}\|=e^{{-\lambda u+\frac{\lambda^{{2}}s}{2}}}{\mathbb{E}}M_{{0}}=e^{{-\lambda u+\frac{\lambda^{{2}}s}{2}}}.$

Zatem

${\mathbb{P}}\Big(\sup _{{0\leq t\leq s}}W_{{t}}\geq u\Big)\leq\inf _{{\lambda>0}}e^{{-\lambda u+\frac{\lambda^{{2}}s}{2}}}=e^{{-\frac{u^{{2}}}{2s}}}.$

∎

5.3. Zadania

Ćwiczenie 5.1

Załóżmy, że $(N_{t})_{{t\geq 0}}$ jest procesem Poissona, tzn. procesem o prawostronnie ciągłych trajektoriach takim, że $N_{0}=0$ , $N$ ma przyrosty niezależne, oraz $N_{t}-N_{s}\sim{\rm Poiss}(t-s)$ dla $t>s$ . Wykaż, że $(N_{{t}}-\lambda t)_{{t\geq 0}}$ oraz $((N_{{t}}-\lambda t)^{{2}}-\lambda t)_{{t\geq 0}}$ są martyngałami względem $({\mathcal{F}}_{{t}}^{{N}})_{{t\geq 0}}$ .

Ćwiczenie 5.2

Wykaż, że $(\exp(\lambda W_{{t}}-\frac{\lambda^{{2}}t}{2}),{\mathcal{F}}_{{t}}^{{W}})_{{t\geq 0}}$ jest martyngałem dla dowolnego $\lambda\in{\mathbb{R}}$ .

Ćwiczenie 5.3 (Prawo iterowanego logarytmu dla procesu Wienera)

Wykaż, że
a) $\limsup _{{t\rightarrow\infty}}\frac{W_{{t}}}{\sqrt{2t\ln\ln t}}=1$ p.n.,
b) $\liminf _{{t\rightarrow\infty}}\frac{W_{{t}}}{\sqrt{2t\ln\ln t}}=-1$ p.n..

Wskazówka:

i) Niech $C>1$ oraz $u>C^{{1/2}}$ . Wykaż, że

$\sum _{{n}}{\mathbb{P}}\Big(\sup _{{C^{n}\leq t\leq C^{{n+1}}}}W_{t}\geq u\sqrt{2C^{n}\ln\ln C^{n}}\Big)<\infty$

i wywnioskuj stąd, że $\limsup _{{t\rightarrow\infty}}\frac{W_{{t}}}{\sqrt{2t\ln\ln t}}\leq u$ p.n..
ii) Wykaż, że $\limsup _{{t\rightarrow\infty}}\frac{W_{{t}}}{\sqrt{2t\ln\ln t}}\leq 1$ p.n. oraz $\liminf _{{t\rightarrow\infty}}\frac{W_{{t}}}{\sqrt{2t\ln\ln t}}\geq-1$ p.n..
iii) Udowodnij, że dla $g\sim{\mathcal{N}}(0,1)$ i $t>0$ ,

$\frac{1}{\sqrt{2\pi}}\Big(\frac{1}{t}-\frac{1}{t^{3}}\Big)e^{{-t^{2}/2}}\leq{\mathbb{P}}(g\geq t)\leq\frac{1}{\sqrt{2\pi}t}e^{{-t^{2}/2}}.$

iv) Wykaż, że dla $C>1$ i $u<1$

$\sum{\mathbb{P}}(W_{{C^{{n}}}}-W_{{C^{{n-1}}}}\geq u\sqrt{1-1/C}\sqrt{2C^{{n}}\ln\ln C^{n}})=\infty$

i wywnioskuj stąd i z ii), że $\limsup _{{t\rightarrow\infty}}\frac{W_{{t}}}{\sqrt{2t\ln\ln t}}\geq u(1-1/C)^{{1/2}}-C^{{-1/2}}$ p.n..

Ćwiczenie 5.4

Udowodnij, że
a) $\limsup _{{t\rightarrow 0+}}\frac{W_{{t}}}{\sqrt{2t\ln\ln(1/t)}}=1$ p.n.,
b) $\liminf _{{t\rightarrow 0+}}\frac{W_{{t}}}{\sqrt{2t\ln\ln(1/t)}}=-1$ p.n..

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

	$\displaystyle{\mathbb{E}}(f(W_{{t}})\|{\mathcal{F}}_{{s}}^{W})$	$\displaystyle={\mathbb{E}}(f(W_{{s}}+(W_{{t}}-W_{{s}}))\|{\mathcal{F}}_{{s}}^{W})$
		$\displaystyle=(2\pi(t-s))^{{-d/2}}\int _{{{\mathbb{R}}^{{d}}}}f(W_{{s}}+x)e^{{-\frac{\|x\|^{{2}}}{2(t-s)}}}dx$
		$\displaystyle=(2\pi(t-s))^{{-d/2}}\int _{{0}}^{{\infty}}r^{{d-1}}e^{{-\frac{r^{{2}}}{2(t-s)}}}\Big(\int _{{S^{{d-1}}}}f(W_{{s}}+y)d\sigma(y)\Big)dr$
		$\displaystyle=(2\pi(t-s))^{{-d/2}}\|S^{{d-1}}\|f(W_{{s}})\int _{{0}}^{{\infty}}r^{{d-1}}e^{{-\frac{r^{{2}}}{2(t-s)}}}dr$
		$\displaystyle=(2\pi)^{{-d/2}}\|S^{{d-1}}\|\int _{{0}}^{{\infty}}r^{{d-1}}e^{{-\frac{r^{{2}}}{2}}}drf(W_{{s}})=c_{{d}}f(W_{{s}})\quad\mbox{ p.n.}.$

	$\displaystyle{\mathbb{E}}\max _{{0\leq n\leq N}}\|X_{{n}}\|^{{p}}$	$\displaystyle=p\int _{{0}}^{{\infty}}\lambda^{{p-1}}{\mathbb{P}}(X^{{}}\geq\lambda)d\lambda\leq p\int _{{0}}^{{\infty}}\lambda^{{p-2}}{\mathbb{E}}\|X_{{N}}\|{\mathrm{I}}_{{\{ X^{{}}\geq\lambda\}}}d\lambda$
		$\displaystyle=p{\mathbb{E}}\|X_{{N}}\|\int _{{0}}^{{X^{{}}}}\lambda^{{p-2}}d\lambda\leq\frac{p}{p-1}{\mathbb{E}}\|X_{{N}}\|(X^{{}})^{{p-1}}$
		$\displaystyle\leq\frac{p}{p-1}({\mathbb{E}}\|X_{{N}}\|^{{p}})^{{1/p}}({\mathbb{E}}(X^{{*}})^{{p}})^{{(p-1)/p}}.$

Wstęp do Analizy Stochastycznej